Использование теории игр для повышения прозрачности моделей машинного обучения
Проблема черных ящиков

Отсутствие прозрачности это одна из ключевых проблем современного машинного обучения. Обученную модель больше невозможно представить в виде набора весовых коэффициентов, как в случае логистической или линейной регрессии. Вместо этого мы видим некий «черный ящик», программный комплекс, который по набору входных данных выдает предсказание. При этом то, что мы возможно сами создали этот черный ящик и можем заглянуть внутрь него не сильно меняет ситуацию. Например, была разработана модель бустинга, ансамбль из нескольких тысяч решающих деревьев. Вполне возможно сгенерировать файл (на несколько мегабайт) с программой на языке Python или C, который будет полностью описывать весь процесс вычисления, но тем не менее этот файл по факту невозможно будет прочитать и интерпретировать.
Отсутствует очевидный способ получить ответы на следующие важные вопросы:
Какие факторы вносят наибольший вклад в предсказание?
Какие факторы бесполезны, и мы можем их исключить?
Какие факторы настолько важны, что имеет смысл инвестировать деньги чтобы улучшить их качество?
Как факторы взаимодействуют между собой?
Как объяснить начальству / бизнес подразделению / внешнему аудитору / регулятору что модель надежна, устойчива и обеспечивает высокое качество предсказаний?
Значимость факторов как средство повышения прозрачности
Одним из способов решить данную проблему является серия разнообразных алгоритмов для вычисления значимости факторов. Таких алгоритмов достаточно много, постараемся перечислить некоторые из них:
Split Feature Importance: сколько раз фактор был использован в модели
Information Gain Feature Importance: на сколько уменьшается энтропия при использовании каждого фактора
Loss Function Change Feature Importance: насколько изменится функция потерь по выборке если мы удалим конкретный фактор
Permutation Feature Importance: насколько изменится функция потерь по выборке если мы перемешаем значения по конкретному фактору
Как мы видим, данные алгоритмы, позволяют вычислить значимость конкретного фактора и частично ответить на первую часть заданных вопросов, о том какие факторы не значительны, а какие вносят существенный вклад. Тем не менее, они ничего не говорят о том, как факторы взаимодействуют между собой и почему модель сработала или не сработала на данном конкретном случае, а именно с этими вопросами чаще всего бизнес приходит к моделисту. Чтобы ответить на эти вопросы, постараемся обратиться к математическому методу известному как теория игр, а конкретно к вектору Шепли — принципу распределения выигрыша между игроками в корпоративных играх.
Вектор Шепли: постановка задачи
В корпоративных играх существует набор игроков, которые могут получить выигрыш (заработать деньги) раздельно или вступая в коалиции, причем объем выигрыша зависит от состава коалиции. Возьмем, например, оркестр из трех музыкантов: барабанщик, гитарист и пианист. Известно, что за вечер в качестве оркестра они могут заработать 15 000 рублей, барабанщик с гитаристом 5 000 рублей, гитарист с пианистом 3 000 рублей, барабанщик с пианистом 0 рублей (нет таких заказов в принципе) и по отдельности барабанщик 2 000 рублей, гитарист 2 000 рублей, пианист 4 000 рублей. Если они решили выступать совместно, как им следует разделить полученный выигрыш?
Более формально если у нас есть множество игроков N (мощностью n) и характеристическая функция ν, которая по любому подмножеству игроков выдает выигрыш (в частности, по пустому множеству выигрыш всегда равен 0), который они могут получить, то каким разумным образом следует разделить между ними этот выигрыш? Т.е. требуется найти функцию φ, которая по номеру игрока i и характеристической функции определяет долю выигрыша игрока в заданной игре. В данном случае под словом «разумный» подразумевается следующий набор аксиом:
Эффективность
Выигрыш целиком и полностью распределяется между игроками, дополнительные суммы также ниоткуда не появляются.
Симметричность
Два игрока вносящих один и тот же вклад, получают один и тот же выигрыш. Т.е. при распределении денег, номер игрока, его имя, репутация и т.п. значения не имеют, имеет значение только его вклад.
Линейность
Если существует несколько отдельных игр, то доля игрока при их объединении будет суммой долей этого игрока в отдельных играх. Аналогично при масштабировании игры (т.е. если все выигрыши увеличились в некоторое число раз), доля каждого игрока также должна соответствующим образом масштабироваться.
Аксиома болвана
Игрок, который по факту не вносит никакого вклада ни в какую коалицию (в том числе сам не может ничего заработать) не должен получить никакой доли общего выигрыша.
Можно доказать математическим образом, что существует только один способ дележа в корпоративных играх, который удовлетворяет всем вышеприведенным аксиомам, он и называется вектором Шепли. Данный результат был получен математиком и экономистом Ллойдом Шепли в 1951 году.
Вектор Шепли: вычисление
Вектор Шепли можно вычислить по следующей формуле:
Сразу обратим внимание, что вычисление проводится по всем подмножествам игроков, не включающим игрока i, т.е. в случае n игроков, для каждого игрока необходимо провести порядка 2^(n-1) вычислений. В целом нахождение вектора Шепли это достаточно сложная задача с вычислительной точки зрения.
Для улучшения интуитивного понимания вектора Шепли, стоит упомянуть о таком понятии, как «синергия коалиции».
Синергией называется выигрыш, который получает коалиция от объединения, т.е., например один игрок зарабатывает 100, другой 200 (300 в совокупности если не объединятся), а вместе 700. Тогда синергия их коалиции 400 = 700 — 100 — 200, т.е. эта сумма, которую они получили за объединение. Любой выигрыш коалиции распадается на сумму синергий (w) его подкоалиций:
получается, что синергия в свою очередь вычисляется по формуле:
Можно показать, что вектор Шепли вычисляется по формуле:
Таким образом синергия каждой подкоалиции поровну делится между игроками в ней участвующими.
Рассмотрим исходный пример с оркестром. Согласно приведенным выше формулам:
Синергия гитариста и пианиста = 3 — 2 — 4 = -3
Синергия барабанщика и пианиста = 0 — 2 — 4 = -6
Синергия барабанщика и гитариста = 5 — 2 — 2 = 1
Синергия оркестра = 15 — 3 — 5 — 0 + 2 + 2 + 4 = 15
Доля барабанщика = 2 + (-6)/2 + ½ + 15/3 = 4,5
Доля гитариста = 2 + (-3)/2 + ½ + 15/3 = 6
Доля пианиста = 4 + (-3)/2 + (-6/2) + 15/3 = 4,5
Использование вектора Шепли для повышения прозрачности моделей
Каким же образом можно использовать вектор Шепли в машинном обучении. Представим себе, что предсказание (в случае регрессии) или скор балл / вероятность (в случае классификации), который выдает модель это совокупный выигрыш коалиции факторов / фичей модели. Наша задача разделить этот выигрыш между факторами и их значениями для каждого конкретного случая.
Зафиксируем конкретный кейс и значения факторов ему соответствующие. Для того чтобы провести дележ и рассчитать вектор Шепли нам нужна характеристическая функция, которая вычисляет выигрыш по каждому поднабору факторов. Для этого пусть значения факторов из поднабора останутся неизменными (равными значениям, зафиксированным в начале абзаца), а значения факторов, не входящих в текущий поднабор, будут случайным образом выбраны из исходной выборки и пусть будет рассчитано соответствующее предсказание модели. Среднее значение предсказания по большом большому количеству значений факторов, не входящих в текущий поднабор, и будут выигрышем по данному поднабору факторов (коалиции). Осталось только рассчитать вектор Шепли, и мы получим разложение текущего скор балла по значениям отдельных факторов. Обращаем ваше внимание, что в случае вектора Шепли, выигрыш в игре без участников (в нашем случае, когда все факторы случайно берутся из выборки) должен быть равен 0, поэтому из всех предсказаний модели нужно перед началом расчета вычесть среднее значение предсказания по выборке.
Рассмотрим, например, модель предсказывающую цену квартиры по 3 факторам: расстояние до центра, площадь кухни, наличие радиоточки. Пусть в нашем случае расстояние до центра 3 км, площадь кухни 5 кв. м, а радиоточка отсутствует. Итоговая цена 10 млн. рублей. Средняя цена квартиры 9 млн. рублей, т.е. нам нужно объяснить +1 млн. Посмотрим, как будет вычисляться вектор Шепли:
Расстояние до центра | Площадь кухни | Наличие радиоточки | Средняя цена |
3 | 5 | 0 | 10 |
3 | 5 | случайное | 10 |
3 | случайная | 0 | 11 |
3 | случайная | случайное | 11 |
случайное | 5 | 0 | 10 |
случайное | 5 | случайное | 10 |
случайное | случайная | 0 | 9 |
случайное | случайная | случайное | 9 |
В данном случае легко видеть, что отсутствие или наличие радиоточки ни на что не влияет, «Расстояние до центра = 3 км» в одиночку приносит +2 млн., «Площадь кухни = 5 кв. м» в одиночку приносит 0 млн., совокупность двух этих факторов приносит +1 млн., т.е. синергия их коалиции равна -1 млн. рублей и таким образом вклады факторов:
для «Расстояние до центра = 3 км» это 2 + (-1)/2 = +1,5 млн. рублей
для «Площадь кухни = 5 кв. м» это 0 + (-1)/2 = -0,5 млн. рублей
для «Наличие радиоточки» это 0 млн. рублей
Т.е. прогноз модели в 10 млн. рублей = 9 (средняя цена) + 1,5 (расстояние до центра) — 0,5 (площадь кухни).
SHAP values
В целом вычисление вектора Шепли в лоб является NP-полной задачей, и для большого числа факторов и строк в выборке по сути невозможно. К счастью, существует множество алгоритмов аппроксимации и ускорений этих вычислений. Так пакет SHAP в Python-е позволяет вычислить shap values для более чем 1000 факторов 100,000 кейсов меньше чем за минуту. Кроме, того данный пакет предоставляет красивую визуализацию, значение которой надеюсь, полностью понятно исходя из описанного ранее.
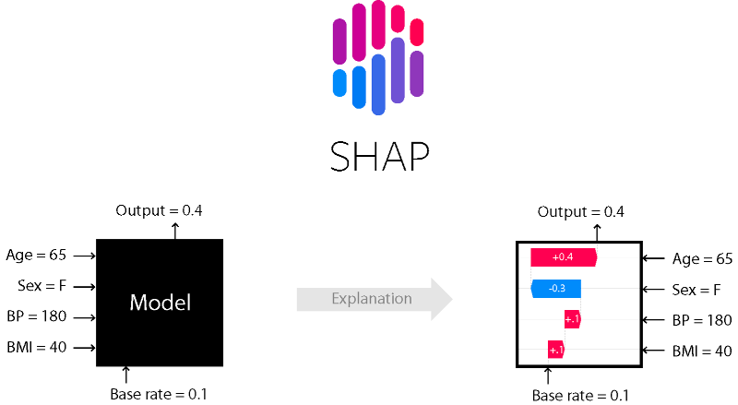
Выводы
Используя идеи, пришедшие из теории игр возможно объяснить вклад каждого отдельного фактора в результат модели для каждого конкретного случая, это позволяет нам ответить на вопросы о том, почему наш «черный ящик» выдал такой результат в данном конкретном случае, исследовать False Positive и False Negative и найти пути улучшения модели. Можно исследовать средний вклад каждого фактора в предсказания и достаточно эффективно объяснить всем заинтересованным лицам почему модель ведет себя тем или иным образом. Таким образом, вектор Шепли помогает нам использовать всю предсказательную мощь «черных ящиков» обеспечивая при этом предсказуемость и стабильность работы модели.
