Искусственные и биологические нейронные сети
Это можно сравнить с поиском Священного грааля, поиск алгоритма по которому работают биологические нейронные сети. Конечно многие скажут, что никакого грааля не существует, это всё легенды, и в искусственных нейронных сетях уже всё реализовано, осталось дождаться развития этой технологии, вычислительных ресурсов и. и всё настоящий искусственный интеллект будет создан. А, разбираться в сложном и запутанном органе для этих целей нет необходимости. Но, надеюсь есть добрая доля искателей приключений которым будет интересны некоторые рассуждения где стоит искать этот «Священный грааль». В статье мы проанализируем и сравним работу искусственных нейронных сетей с гипотезами о том как работают биологические нейронные сети, и конечно, сопроводим это практическими опытами, разберем новую искусственную нейронную сеть, которая по своему принципу работы ближе к биологическому аналогу.
Как же работает искусственная нейронная сеть?
Начнём мы с анализа искусственных нейронных сетей. Нет здесь не будет описаний принципов работы сетей, лучше о них расскажут другие многочисленные источники, здесь мы попытаемся понять некую фундаментальную суть их работы в части распознавания образов. Это очень наглядно демонстрирует одни простой пример:
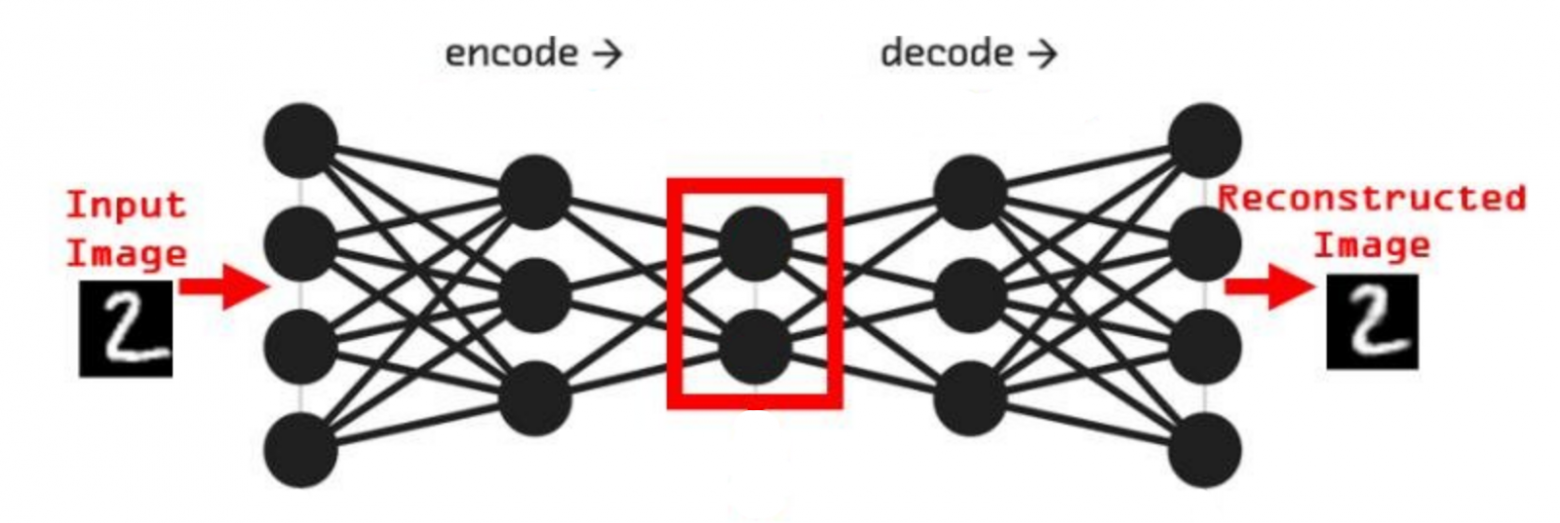
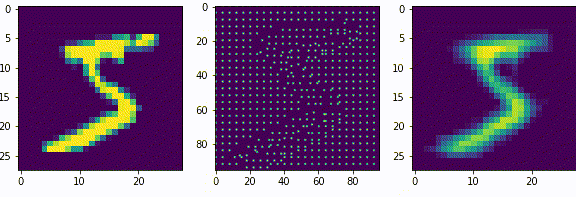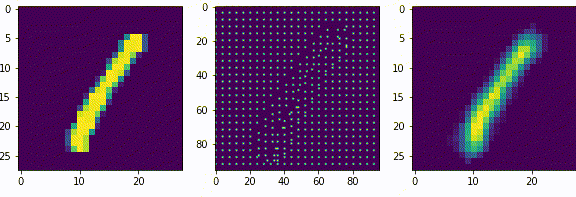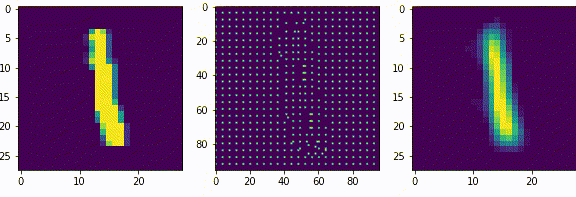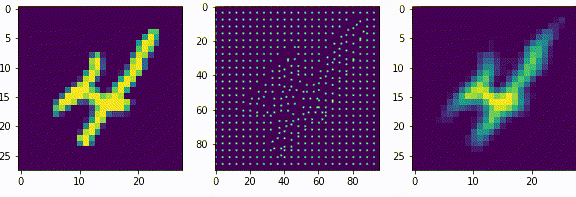
Представим сеть состоящую из двух частей энкодера и декодера, на вход которой будет подаваться примеры из набора рукописных цифр MNIST и на выходе соответственно дублируем вход. Обучать её будем классическим методом, обратным распространением ошибки. Самая узкая часть сети, самый маленький слой расположенный между энкодером и декодером будет иметь всего 2 нейрона. После обучения получится так, что эти 2 нейрона будут нести в себе информацию, так скажем, кодировать образы множества начертаний всех цифр. Если по оси x разместить активность одного нейрона, а по y активность другого нейрона, то на диаграмме можно отметить какие точки соответствуют каждому классу, а с помощью декодера воспроизвести начертание цифры соответствующее точкам.
Замечательный интерактивный пример этого можно попробовать здесь
То, что мы получили, специалисты называют Малое Репрезентативное Представление (МРП), «малое» — потому, что у нас всего 2 вещественных числа отражают вектор из 784 вещественных чисел, а «репрезентативное» — оно потому, что отражает внутри сети внешний мир, то есть зная лишь эти два значения, мы можем оценить что в данный момент «видит» сеть, какую цифру и даже примерную форму её начертания. Можно сказать, что Малое Репрезентативное Представление (МРП) это некая модель мира, только сети пришлось сделать очень простую модель, малую, всего два числа, хотя внешний мир более сложен и представляет собой наборы из 784 вещественных чисел.
Давайте взглянем подробнее, что из себя представляет эта Малое Репрезентативное Представление (МРП), мы видим несколько областей которые будут соответствовать определённым классам и соседние точки будут соответствовать очень близким по начертанию цифрам. Получается МРП может помочь существенно упростить процесс обучению распознавания. Мы можем взять обученный декодер, отбросив энкодер, добавить небольшой персептрон и достаточно быстро новую сеть научить распознавать рукописные цифры (это называется transfer learning, или перенос обучения), то есть сначала наша сеть, или её первая конфигурация обучалась только на изображениях без связи их с фактическим числом, такое вот самообучение (без учителя) для получения МРП, а затем следующая конфигурация используя полученное МРП, обучается на сопоставлении изображения и метки цифры, обучение с учителем, и делает это значительно быстрее, чем сеть которая будет обучаться сразу на сопоставлении.
По сути здесь класс цифры определяется некоторыми диапазонами активности двух нейронов. Эти диапазоны или области как мы видим на диаграмме, можно назвать некими эмбеддингами, представительствами классов внутри сети, которые сформировались в процессе самообучения.
Далее мы поговорит о том, что из себя представляет Малое Репрезентативное Представление (МРП) в биологических сетях, в мозге, как в нём представлены эти эмбеддинги, но для начала выделим некоторые качества этих сущностей для искусственных нейронных сетей. Во-первых, в МРП задействован слой целиком, все нейроны слоя имеют значение. Представим что мы убрали из сети один из двух нейронов, детектировать точно что «видит» сеть по одному нейрону будет проблематично, не всегда можно ответить даже на вопрос, а видит ли сейчас сеть, например, цифру »5». Да, существует прунинг, но он возможен только при избыточном количестве нейронов, когда можно убрать нейроны без последствий для МРП. Во-вторых, чем больше нейронов в слое задействованном в МРП тем сложнее выделить фичи, так как каждый нейрон создает свое измерение в пространстве представительств классов, 2 нейрона — 2 измерения, 10 нейронов — 10 измерений… и все 10 будут взаимозависимы. В третьих, очевидная для искусственных сетей вещь, все нейроны слоя или даже всей сети, при каждом такте обучения вовлечены в него, каждый нейрон получит свою корректировку весов.
В отличии от классических искусственных нейронных сетей в биологических сетях отражён нейроно-детекторный подход. В биологической сети нейрон выступает как детектор определённого признака или группы признаков. Можно сказать, что за фичи или эмбеддинги здесь отвечают отдельные нейроны. Это подтверждается многочисленными экспериментами, существует даже шуточное название для этого явления — «бабушкины нейроны», которое говорит о том, что любому образу в нашем мозге будет соответствовать активность определенной клетки, не исключено даже наличие такой клетки для образа нашей бабушки. Конечно, когда мы говорим «нейрон» в данном случае, то подразумевается целая группа активных нейронов. Во-первых, прежде чем возбуждение достигнет пресловутого бабушкиного нейрона оно пройдет через ряд других нейронов, во-вторых, обычно за каким-либо образом стоит активность целой группы распределенных по коре нейронов, нейронного ансамбля или паттерна активности.
Формальный нейрон искусственных сетей достаточно хорошо отражает принцип работы биологического нейрона, веса формального нейрона — отражают размеры порций медиатора выделяемые в синаптическую щель при активации синапса, а совокупное влияние нейромедиатора приводящие к возникновению потенциала действия отражено в пороговой функции формального нейрона. Всё замечательно, но
при картировании первичной зрительной коры («Глаз, мозг, зрение» Хьюбел Дэвид, Торстен Визель) фиксируется активность нейронов на определенные раздражители, к примеру, различной ориентации линии, отрезки, концы отрезков. И дело здесь не в том, что нейроны коры работают по другим принципам, дело, скорее, в самой организации этих нейронов.
В общем, можно сказать, что формальные нейроны искусственных сетей более эффективно работают с информацией чем биологические нейроны, например, как мы убедились, для кодирования множества начертаний рукописных цифр может потребоваться всего два нейрона, а при кодировании по нейроно-детекторному принципу потребуется минимум 10 нейронов хотя бы закодировать 10-ть классов цифр, не говоря уже о различных формах начертаний этих цифр. Тогда возникает резонный вопрос: зачем вообще пытаться понять этот принцип, зачем искать этот Грааль?
Во-первых, работая над созданием модели нейронных сетей в которых будет применяться нейроно-детекторный подход мы можем больше узнать о принципах на которых работают биологические нейронные сети. Во-вторых, хоть эволюционный процесс не идеален и не всегда приводит к оптимальным решениям, но в вопросе сбережения энергии и эффективности работы мозга эволюция была успешна. При нейроно-детекторном подходе нет необходимости активировать все нейроны при обучении и работе модели, да, для математической модели это не даёт особых преимуществ в эффективности, а при реализации такой модели в «железе» может дать существенно. В третьих, представьте насколько удобно использовать нейронную сеть состоящую из нейронов-детекторов, мы можем оценить о чём «думает» в данный момент сеть по активности нейронов, мы можем понять как она принимает решения, мы можем управлять этим решениями просто активировав нужные нейроны. В четвертых, возможность обучения с одного раза (one-shot learning). Если у Вас есть нейрон-детектор реагирующий на слово «стол» и нейрон-детектор реагирующий на изображение стола, Вам не составит труда создать между ними связь. В пятых, это была бы более стабильная модель в вопросе дообучения, переобучения (в хорошем смысле этого слова), а также физическом разрушении, если повредить нейрон-детектор ответственный за цифру »5», оставшиеся нейроны позволяют на хорошем уровне распознавать цифры, банально из-за отсутствия тесного взаимодействия уровня активности нейронов при детекции. Еще несколько доводов в пользу перспектив таких сетей: это гибкость их управления в динамике, а значит возможность создавать алгоритмы высокоуровневого управления этих сетей, подобно тому как эмоциональные системы управляют памятью и реакциями в нервных системах животных и человека. Еще есть возможность оценить новизну поступающей информации на любом абстрактном уровне на котором работает сеть, если в нашей системе существует детектор который реагирует на внешний раздражитель, и мы можем оценить степень этой реакции, а значит оценить близость внешнего раздражителя к внутренней памяти системы, что и будет оценкой новизны. Если критерии новизны станут важными для управления нейронной сетью то, это должно приблизить нас пониманию того как создать настоящий искусственный интеллект, ведь в поведении человека и животных новизна это очень важный фактор.
Как кодируют информацию биологические нейронные сети?
Малым Репрезентативным Представлением (МРП) для мозга является SDR (Sparse Distributed Representation) или Разреженное Распределенное Представление (РРП). «Разреженное» — значит, что только небольшое число нейронов активны одновременно, а «распределенное» — означает, что активность эта распределена по ткани равномерно. Но к этому термину можно применить и слово «малое», так как любое представление в мозге всегда будет иметь меньшую размерность чем внешний мир. На самом деле разреженность и рапределённость является лишь результатом работы нейро-детекторного подхода, мы на практике увидим как это происходит.
Многие могут связать понятие SDR с работами Джеффа Хокинса (Jeff Hawkins), так как он активно писал о SDR и применял его в своей модели Hierarchical Temporal Memory или HTM, но SDR это общий экспериментально наблюдаемое явление свойственное для нервных систем всех млекопитающих (и насекомых) от мышей до человека. Автор не разделяет взглядов Джеффа Хокинса относительно HTM, по причине невозможности существования HTM-нейрона (так как описывает его Джефф) который не вписывается в общепринятую нейронную парадигму — опять же по мнению автора.
Попробуем создать искусственную нейронную сеть основанную на нейроно-детекторном подходе, мы будем руководствоваться и вдохновляться знаниями о биологическом мозге и принципах его работы.
Схема и организация сети
Нет инструмента который бы одинаково хорошо работал с обычными и разреженными данными одновременно, поэтому механизм работы нейронов-детекторов связанных с внешними данными и данными возникающими внутри сети будет различаться. Первый слой нашей модели будет получать обычный вход, в данном случае 784 мерный вектор представляющий собой цифру из набора MNIST, и на выходе мы получим разреженность (SDR), а все последующие слои будут получать SDR и выдавать SDR. По существу, главная задача первого слоя преобразовать данные в разреженное представление, в обучении этого слоя нет необходимости. Перебрав множество вариантов к принципам построения этого слоя я пришёл к самому простому и оптимальному варианту, применению нескольких ядер свёртки выбранных вручную. Шестнадцать ядер размером 5×5.
Выбор ядер определяется распространенностью паттернов в данных которые мы будем обрабатывать. К примеру, для цифр из MNIST характерны пустые, незаполненные пространства, то есть почти в каждом примере можно найти ни одну область 5×5 где все пиксели будут равны 0, такое ядро разумно внести в наш набор. Также цифры выполнены линиями, разной толщины и ориентации, что определяет ещё некоторые варианты ядер — линии разной направленности. Здесь важно, чтобы набор оказался максимально разнообразным.
Как мы знаем для первичной зрительной коры свойственны нейроны-детекторы линий различной ориентации, каждая колонка фактически настроена на свой раздражитель. Хьюбел Дэвид и Торстен Визел в своей работе по картированию первичной зрительной коры ввели термин — гиперколонка или модуль, что представляет собой совокупность всех колонок которые имеют общее рецептивное поле, к примеру, небольшую область на экране где проецируются светящиеся линии различной ориентации. То есть в составе модуля (название термина модуль, для меня более приемлем, чем гиперколонка, так как нет созвучия с темином колонка, поэтому здесь и далее буду применять это название) присутствуют все представительства ориентаций линий для обоих глаз и это составляет около 1000 колонок.
Гиперколонка или модуль, иллюстрации из книги «Глаз, мозг, зрение» Хьюбел Дэвид
В нашем варианте будет всего 16-ть нейронов-детекторов в модуле (да, наш нейрон-детектор эквивалентен одной колонке в коре), каждый будет соответствовать своему ядру. Каждый модуль будет отвечать за свой фрагмент картинки 5×5, причём, как и в коре рецептивные поля колонок обычно пересекаются, поэтому мы будем разбивать общую картинку на фрагменты 5×5 шагом 1.
Модульный принцип организации фундаментален для нашей сети, как для первого слоя так и для последующих. Главное особенность модульного построения это то, что победитель в модуле всегда один. То есть среди нейронов-детекторов модуля идет конкуренция которая будет определять какой нейрон в модуле будет иметь приоритеты в активации и обучении. Подобно тому как у живых колонок существует латеральное ингибирование (боковое торможение), за счёт которого колонки со слабой активностью полностью подавляется, а за счёт эффекта иррадиации (стремления возбуждения распространится) победившие колонки укрепляются в своей активности.
В предыдущих своих работах я описывал опыты с пиксельным шейдером в котором реализованы латеральное ингибирование и иррадиация, которые показывает, что любая изначальная активность преобразуется в небольшие точечные распределенные очаги. Вот и причина распределённости и разреженности.
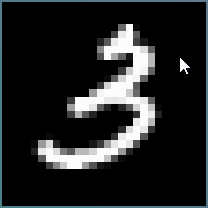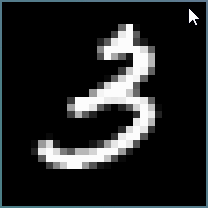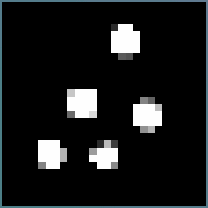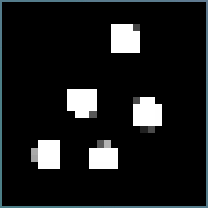
В коре нет явных границ модулей, но при создании математической модели нейронных сетей мы можем её сделать более точной и структурированной, в какой-то степени в этом наше преимущество. Поэтому латеральное ингибирование можно заменить правилом: в модуле может быть активен только один нейрон-детектор.
Первоначальную активность каждого нейрона в первом слое оцениваем по манхэттенскому расстоянию, но в конечном итоге, в каждом модуле будем считать активным только один, тот который будет иметь максимальную близость со входным вектором в модуле. Работа модуля может напомнить принципы работы сети Кохонена, наша будущая модель как будто состоит из множества малых сетей Кохонена.
Примеры работы первого слоя. Входной вектор 28×28, ядро 5×5 шагом 1, в модуле по 16 нейронов-детекторов, в итоге получаем результат 24×24х16, которую преобразуем в планарный вид 96×96. Этот выход первого слоя представляет собой SDR для любого входного вектора.
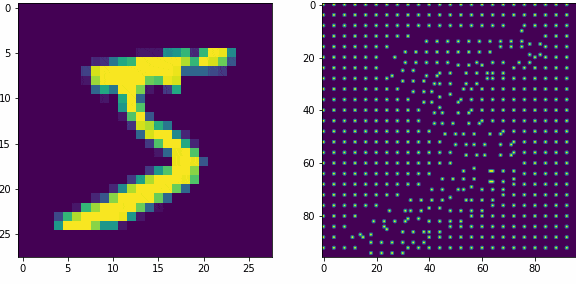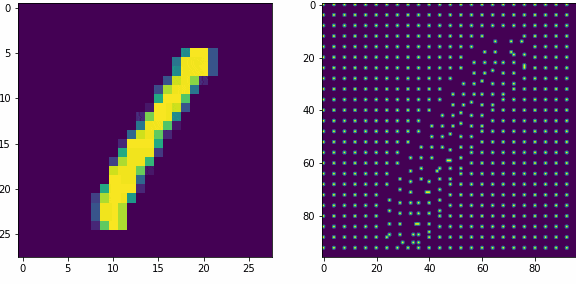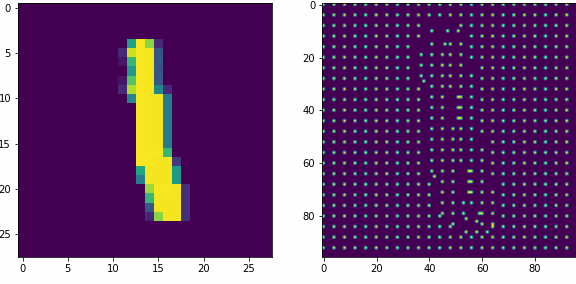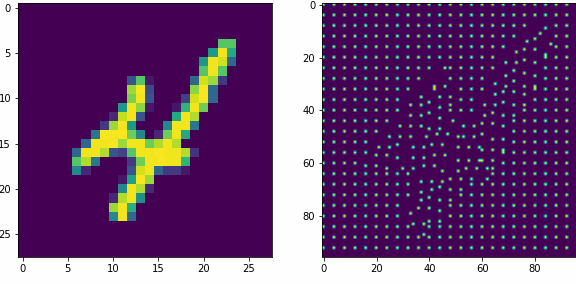
Планарность или представление данных в двумерном виде в нашем случае очень важна, так как последующие слои будут получать данные именно таком виде, еще это более наглядно и похоже на то как представлены данные в коре мозга.
Как уже оговаривали ранее, главная задача первого слоя это представление внешних раздражителей в виде SDR. Так как количество нейронов в модуле 16, то соотношение единиц и нулей в полученном SDR всегда будет 1 к 15-ти, для любого входного вектора. Наш первый слой не обучается, только преобразует данные.
Так как слой производит обычное преобразование данных, то возможно получить и обратное преобразование, которое показывает, что трансформация данных происходит с некоторой потерей качества, но это необходимая жертва, так как полученные данные будут абсолютно нормализованы, полная сумма полученного вектора будет всегда одинакова, независимо от того, что подано на вход сети. В биологии подобные преобразования происходят уже на уровне сетчатки глаза, благодаря on-, off-клеткам, независимо от того, что проецируется на сетчатку глаза общая активность нерва идущего от глаза будет постоянна.
Нейроны последующих слоев будут получать на вход разреженные вектора. Если нейроны первого слоя, можно сказать, выделяли признаки из входных данных (палочки, точки, пустоты), то нейроны последующих слоев будут генерализировать то есть обобщать выделенные признаки.
Неконтролируемое обучение снизу-вверх
Самообучение это главная подсказка того где искать наш Священный грааль. Можно сказать, что обычно обучение у животных и человека в своем большинстве происходит на данных которые не являются размеченными, зачастую эти данные не полные и зашумлены. А метки появляются в процессе обучения лишь иногда, в форме сопоставления модальностей, то есть обучение по разметке, контролируемое обучение является лишь вспомогательным, так как в основе лежит самообучение.
Если говорить о задачи распознавания образов, то по существу нам нужен алгоритм который позволит формировать разнообразный набор нейронов-детекторов, которые реагировали бы на явно выраженные представителей своих классов. Ранее в своих изысканиях я использовал алгоритм сетей Кохонена и его вариации [https://habr.com/ru/post/562908/], но он плохо работает с разреженным представлением, что не позволило мне создать многослойный вариант сети. Да и нейрон этой сети свою активность определяет по манхэттенской близости, но я склонялся к более простой версии нейрона, как простого сумматора.
И решать задачу классификации на простых сумматорах оказалась очень просто. Меня заинтересовала статья, которая рассказывала о успешной кластеризации MNIST с помощью спайковых сетей, решение было для меня очень большим, громоздиким и сложным.
Поэтому я попытался реализовать механику этой кластеризации без чего-либо лишнего, результат уместился буквально в несколько строк кода (ссылка на Google colab).
Веса сети после 10 000 примеров MNIST
В примере выше веса нейронов, которых в слое 256 (16×16). За такт сети во всём слое может обучаться только один, самый активный нейрон.
Обучение происходит по очень простой формуле:
map[:, winner] += rate * (inp - 0.5)к весам победителя прибавляем произведение коэффициента ставки обучения (rate=0.2) и разности вход минус 0.5. Почему именно 0.5? — Это банально среднее значение от диапазона входа, он является вещественным числом от 0 до 1. Назовём это число — целевая интенсивность. Целевая интенсивность позволяет провести границу между слабым и сильным входом. По сути эта формула приводит к ослаблению слабых входов и усилению сильных. И чем слабее вход тем мы сильнее уменьшаем связанный с ним вес и наоборот. Конечно, в связи с этим для этого алгоритма подойдут не все данные, там где число в векторе не означает только интенсивность, а несёт более сложную информацию вероятнее всего лучше применять сети Кохонена, но для MNIST это работает достаточно хорошо. Также этот алгоритм имеет явное преимущество, здесь практически отсутствует проблема «суперпобедителя» или лидера. Суть её в том, что выделяется один нейрон который побеждает чаще всего и часто забирает себе всё обучение. Благодаря обучению соседеи в сетях Кохонена эта проблема не проявляется явно. Дело в том, что при использовании вышеописанного алгоритма если стартовая сумма весов достаточно большая, то чем больше обучается нейрон тем меньше уровень его активации на входной вектор, по сравнению с менее обученными нейронами, тем самым у менее обученных нейронов будет больше шансов на победу. Это имеет ключевое значение в начале обучения, когда нейрон только приобретает свою специализацию. Поэтому логичнее всего было сделать значение всех весов при инициализации сети равными единице.
При рождении мозг имеет максимальное число нейронов и первые дни и недели разворачиваются максимальное число синаптических связей. Далее в процессе роста и обучения происходит общая деградация и утрата синаптических связей, а также потеря нервных клеток. Этот процесс называется прунинг и особо большие его масштабы для человеческого мозга проходят к первым трем годам после рождения. Прунинг позволяет более точно специализироваться нейронам, и это можно сравнить с тем, что происходит в нашем алгоритме кластеризации, изначально все веса равны 1, то в процессе обучения лишнее сводится к нулю.
Но у этого алгоритма есть недостаток, это стремление к наименьшей сумме весов, при все большем обучении уровень активации будет снижаться, также будет снижаться и сумма весов, и для победы нейроны будут специализироваться на примеры с всё меньшей суммой.
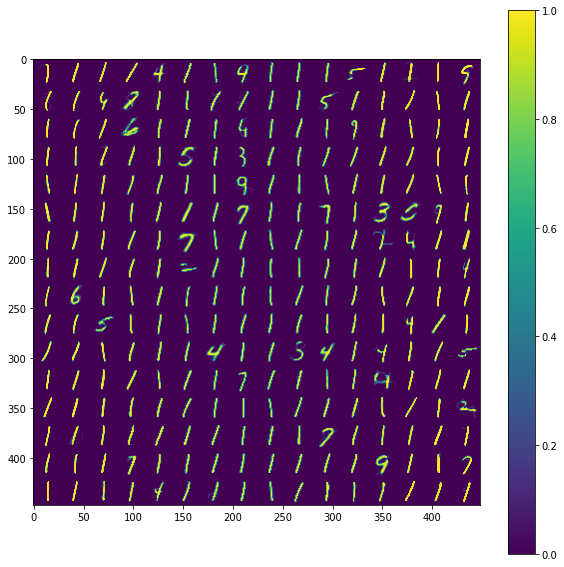Веса сети после 10 эпох на всех 60 000 примерах
Для устранения этой проблемы напрашивается решение о нормализации входного вектора, причем приведение суммы входного вектора к константе. И лучшее для этого решение это SDR.
Но, на самом деле простое сочетание этого алгоритма и SDR не решает проблемы снижения общей суммы весов, хотя разнообразие классов будет сохранятся. Необходимо привнести в алгоритм еще большей стабильности.
Общая идея работы биологического нейрона заключается в том, что он укрепляет в регулярно повторяющиеся связи, а редко используемые связи деградируют и теряются, формируются некие устойчивые пути распространения нервных сигналов. Для реализации этого необходимо вести некую статистику для каждого синапса, насколько часто и эффективно он используется. Поэтому помимо карты весов у нас будет карта «температурного следа» или trace, значение этой карты будут в диапазоне от 0 до 1. Каждый раз когда оба нейрона будут активны соединяющий их синапс будет прибавлять к trace +0,3, но при других тактах сети значение trace будет постепенно убывать на -0,001. Таким образом синапсы которые будут регулярно эффективно использоваться будут иметь высокий trace близкий к 1, напротив для синапсов которые практически не используется trace будет равным нулю или близким к нулю значению. Этот показатель будет оказывать прямое действие на значение веса синапса, так как часто используемые синапсы следует усиливать. Окончательная формула для полученного алгоритма имеет следующий вид:
map[winner,:] = (1 - rate)*map[winner,:] + rate*(inp - 0.5) + trace[winner,:]*rateПомимо известной формулы, здесь при победе веса нейрона увеличиваются на произведение trace и rate тем самым часто используемый синапс усиливается, в противовес этому происходит регулярная деградация синапсов, их веса уменьшаются по модулю (1 — rate)*map[winner,:]. Так как постоянный рост в биологических клетках невозможен, всегда есть некий ограниченный ресурс, поэтому существует гетеросинаптическая конкуренция. Также веса ограничены в диапазоне от -1 до 1, где -1 — это максимально сильный ингибирующий синапс, а 1 — это максимально сильный побудительный синапс.
Описанный алгоритм достаточно прост и позволяет производить самообучение сети даже организованной во множество иерархических слоёв.
Далее давайте рассмотрим конкретную конфигурацию многослойной сети для примера.
Для рассматриваемого варианта сети модули следующего слоя также будет содержать по 16 нейронов-детекторов, у которых будет иметься общее рецептивное поле. Рецептивное поле нейрона будет иметь размер 20×20, что составляет 25 (5×5) модулей предыдущего слоя. Рецептивные поля модулей будут пересекаться с шагом в 4. Итого следующий слой будет содержать 400 (20×20) модулей по 16 нейронов, всего 6 400 (80×80) нейронов. Напомню первый слой составляет 96×96 (9 216) нейронов.
По похожей схеме добавим еще два слоя, в первом из них размер модуля будет 16 (4×4) нейронов. Третий слой размер рецептивного поля 20×20, шаг 4, итого 64×64 нейронов. Четвертый слой — рецептивное поле будет охватывать весь предыдущий слой 64×64, но размер модуля мы сделаем 36, фактически активность этого слоя будет охарактеризовано только одним нейроном из 36, чтобы получить четкий выраженный детектор одной цифры. И последний пятый, выходной слой будет содержать только 10 нейронов по количеству распознаваемых классов. Этот слой необходим чтобы сопоставить результат работы предыдущих слоёв и метки цифры. Этот слой будет иметь только один модуль, соответственно возможна активность только одного нейрона из этого слоя. Каждый нейрон выходного слоя будет иметь одинаковое рецептивное поле размером 6×6 (=36).
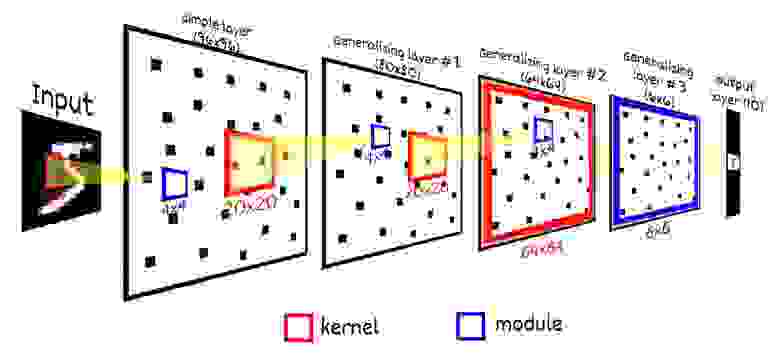
В итоге получается схема: 28×28 (рецепторы) → 96×96 (первый слой, необучаемый, просто преобразует входной сигнал в SDR) → 80×80 (второй слой) → 64×64 (третий слой) → 6×6 (четвертый слой) → 10 (выходной слой). Многослойность данной сети выбрана для демонстрации всех аспектов её работы, в частности «глубокого обучения», для задачи MNIST возможно использовать и более простую конфигурацию.
Выходной слой имеет всего 10 нейронов по количеству распознаваемых классов, все нейроны выходного слоя включены в один модуль. Это значит, что все нейроны выходного слоя имеют общее рецептивное поле равное размеру предыдущего слоя (в данном примере 6×6), также может быть активным только один нейрон выходного слоя.
Предпоследний слой состоит из одного модуля, в нем будет формироваться при самообучении некое представление, каждый из 36 нейронов будет реагировать на свой выбранный тип входного сигнала, обучение последнего же слоя происходит на сопоставлении полученного представления с меткой класса представляемого сети примера. Если метка совпала то увеличиваем вес синапса на rate (0.1), а для всех остальных синапсов которые связаны с другими классами вес снижается на тоже значение только деленное на общее количество классов, то есть на число меньшее в десять раз.
Итогом, самообучение на 5 000 примерах предъявленных сети по одному разу, качество составляет примерно 77%. То есть мы явно видим, что самообучение работает и происходит выделение классов цифр даже без привязки к метки. Но мы можем улучшить этот результат распространив влияние метки класса глубже в слоях.
Контролируемое обучение или обратное распространение влияния
Алгоритм обратного распространения ошибки (backpropagation, бэкпроп) для коннекционных нейронных сетей стал невероятным мощным двигателем машинного обучения, благодаря нему искусственные нейронные сети сдали давать потрясающие результаты. Но этот алгоритм не сочетается с тем, что мы знаем о биологической нервной системе. И вопрос не в распространении сигналов назад по сети, а в том, что нужно передавать достаточно много информации, нужно передавать значение ошибки, и пока не известны в биологии механизмы, механики или органеллы которые даже бы производили бы оценку этой самой ошибки. Существует множество статей которые предлагают якобы близкие к биологии варианты бэкпропа, но все это, если оценивать со стороны биологии истории про сову и глобус.
С одной стороны между различными областями коры участвующей в иерархической обработки информации, как у аналогов слоёв в искусственных нейронных сетях, есть обратные связи и их иногда насчитывают в несколько раз больше чем прямых связей. Происходит постоянная циркуляция возбуждения между участками коры — реверберация. Но каких-то сложных вычислений при этом не производится. Вычисления производятся на органелле — мембрана и алгоритм этих вычислений определён моделью Ходжкина — Хаксли, всё, в этой системе знаний нет места бэкпропу и вычислений ошибок.
И всё таки нейрон находящийся на низком уровне иерархии имеющий ограниченное рецептивное поле какой бы у него не был хороший алгоритм самообучения эффективно обучаться не может без высокоуровнего дирижера, без подсказок исходящей от общей поставленной задачи или цели.
Модульная организация сети и SDR позволяет нам применить алгоритм обратного распространения влияния или backpreference. Нейроны в модуле конкурируют между собой, так как в модуле может быть только один победитель, какой именно нейрон победит определяют восходящие связи и их веса, но возможно благодаря нисходящим связям дать некоторым нейронам в этой борьбе преимущество. Возможно взять любой нейрон последнего слоя и оценить активность каких нейронов предыдущего слоя вероятнее всего приведут этот нейрон к победе, и далее так можно спускаться на более нижние уровни.
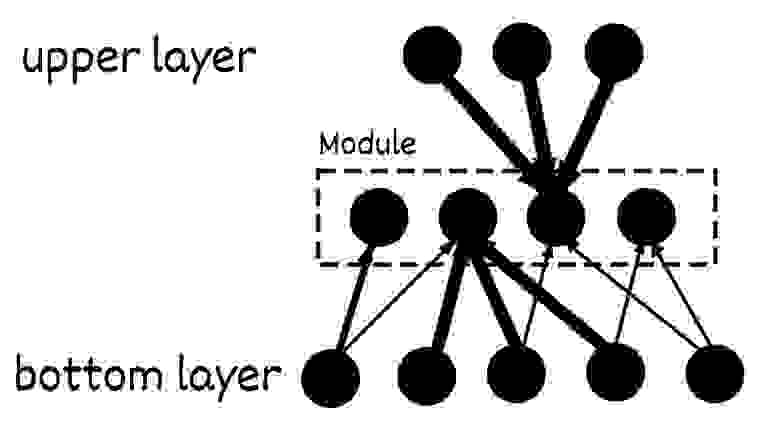
Зная метку класса мы можем выбрать нейроны последнего слоя которые наиболее релевантны этой метке, далее двигаясь вниз от слоя к слою обозначать те нейроны которые в конце концов дадут преимущество нужным нейронам последнего слоя, затем этим нейронам дадим преимущество в победе добавив некоторое значение к итоговой сумме их активации. Получается мы лишь немного вмешиваемся в процесс самообучения, направляя его в более подходящее русло. Мы можем регулировать то на сколько контролируемое обучение будет оказывать влияние на неконтролируемое. Разумно если контролируемое обучение будет сильнее действовать на последних слоях, а самообучение будет действовать больше на первых слоях которые ближе ко входу к рецепторам.
В нашем примере есть три обучаемых слоя, на последний, третий из них контролируемое обучение действует с коэффициентом 1, что говорит 100% выиграет тот нейрон который получит преференции. Для второго слоя коэффициент составляет 0.5, и на первом только 0.1, здесь большее преимущество у самообучения.
Это очень гибкое сочетания контролируемого и неконтролируемого обучения, можно в любой момент полностью отключить контроль и дать самообучению управлять, а когда появится необходимые метки добавить в обучение контроля. Это очень похоже на то как работает и учится биологический мозг.
В начале обучения когда выходной слой еще не определил корреляцию нейронов последнего слоя и меток класса, контролируемого обучения вообще не происходит, только за счет самообучения формируются слабые соотношения, которые затем подхватываются контролируемым самообучением и укрепляются.
Результат с применением контролируемого обучения на 5 000 примерах предъявленных сети по одному разу, качество составляет примерно 93%. Конечно алгоритм по метрикам качества уступает коннекционным нейронным сетям с бэкпропом, но это очень достойный результат учитывая, что в алгоритме нет никаких методов сходимости и вычисления ошибки. Увеличение размерности сети, а значить её потенциальной ёмкости при тех же параметрах тренировки может немного улучшить результат по качеству.
Интерпретируемость искусственной нейронной сети на базе нейро-детекорного подхода
Вопрос интерпретируемости сети очень важен, не достаточно взять модель обучить её на большом количестве данных и полностью довериться ей, особенно если речь идет о жизни и здоровье людей. Необходимо хорошо понимать почему эта модель принимает те или иные решения, должна быть возможность предсказать её действия на любой внешний стимул. В это нейронным сетям основанным на нейро-детекторном подходе не будет равных.
Мы уже затрагивали тему интерпретируемости говоря о малом репрезентативном представлении, в примере где латентное пространство имеет всего два измерения как в случае двух нейронов между энкодером и декодером, в этом примере мы легко можем интерпретировать результата обучения, но только одного самого узкого слоя. Но например, в задачах распознавания лиц, латентное пространство достаточно большое и имеет, например, 18 параметров, представить в наглядном и читабельном виде 18-мерное измерение и сопоставить с образами лиц будет достаточно сложно, не говоря уже о других слоях сети.
Для сетей на базе нейро-детекторного подхода легко интерпретировать результаты, возможно провести обратное преобразования и получить значения активности рецептивного поля которая вероятнее всего приведет к активности конкретного нейрона, причем это можно сделать для любого нейрона любого слоя. Фактически алгоритм обратного распространения влияния и производит обратные преобразования, мы просто применим его для интерпретации результатов обуче
