Интерполяция: рисуем плавные графики с помощью кривых Безье
Доброго времени суток, харбачитатель.
В этой статье мне хотелось бы рассказать об одном придуманном когда-то алгоритме (или скорее всего — переизобретённом велосипеде) построенного плавного графика по заданным точкам, используя кривые Безье. Статья была написана под влиянием вот этой статьи и очень полезного комментария товарища lany, за что им отдельное спасибо.
Постановка задачи
Есть массив Y-ков точек, расположенных равномерно по оси X. Нужно получить плавный график, который проходит через все заданные точки. Пример на рисунке ниже:
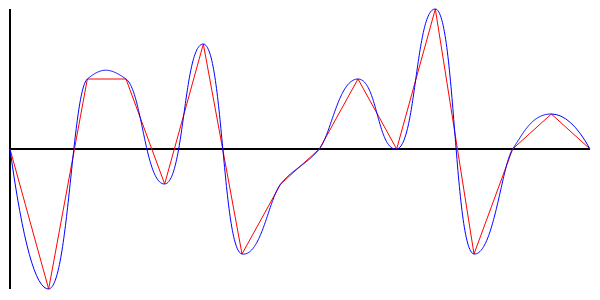
Всех, кому интересно, прошу под кат.
Существует ряд стандартных решений для проведения плавной кривой через точки (по этому поводу много интересного написано в уже упомянутой статье) таких, как например, интерполяции сплайнами. Когда на третьем курсе был придуман этот алгоритм, слово «интерполяция» вселяло в меня ужас, а гугление по запросу «сглаживание графиков» не давало посильных пониманию результатов. Но как-то я дошел до кривых Безье и уж очень они мне понравились. Рисует быстро, алгоритм интуитивно понятный… Что еще надо для счастья. Ну и как-то понеслось.
Основная идея
Разобью идею на три подпункта, чтобы было понятней и читабельней.
- О кривых Безье хорошо написано на вики и на javascript.ru. Если внимательно читать, то можно обратить внимание, что кривая Безье выходит из первой точки касательно к прямой начальная_точка-первая_опорная_точка. Аналогично и в конце — кривая заходит касательно прямой последняя_опорная_точка-конечная_точка. Таким образом получается, что если у нас одна кривая заканчивается в точке А и зашла касательно к прямой а, а другая кривая выходит из этой точки А касательно к той-же прямой а, то этот переход между двумя кривыми Безье у нас получится плавным.
- Исходя из первого пункта получается, что у нас опорные точки слева и справа относительно точки А должны лежать на одной прямой. Поразмыслив немного, было решено, что эта прямая должна быть такой, чтобы ∠BAB1=∠CAC1 (рисунок ниже), где точки B1 и C1 — опорные.

- Расстояние от точки А до точек B1 и C1 было решено взять равным половине шага по X между точками B и A, A и C, и т.д. Мне сложно как-то обосновать такой выбор, но важно, чтобы это расстояние было меньше, чем шаг по X между точками А и B, иначе может получится что-то такое, как на рисунке ниже. Важно понимать, что чем больше будет это расстояние, тем более извилистой будет кривая и наоборот. Расстояние в половину шага по X мне кажется оптимальным, но тут уже возможны варианты.

Таким образом получается, что задача сводится к поиску прямой (B1C1) и, собственно, опорных точек B1 и C1, по которым мы потом будем строить кривые Безье.
Поиск прямой
Как известно, прямая на плоскости выражается формулой y=kx+b, где k — тангенс угла наклона прямой к оси Х. Когда мы найдем k, то зная, что прямая проходит через точку А, и зная ее координаты, мы легко можем найти b: b=YA-kXA. Таким образом все сводится к поиску коэффициента k.Поиск коэффициента k
Скажу наперед, что k = tg (φ) = tg ((α-β)/2) = (Sqrt ((ΔX2+(YA-YB)2)*(ΔX2+(YA-YC)2))-ΔX2-(YA-YB)*(YA-YC)) / (ΔX*((YA-YB)-(YA-YC))), где ΔX — расстояние по Х между точками (напомню, что у нас точки расположены равномерно по Х). Ниже представлено математическое доказательство правильности формулы, но если вы не в настроении, то можете его просто пропустить.

- Пускай угол ∠O1BA=α, а угол ∠O2СA=β.
Тогда ∠BAO1=90o-α; ∠CAO2=90o-β, так как △ABO1 и △ACO2 — прямоугольные. - (1) ∠B1AС1=∠B1AB+∠BAO1+∠O1AС+∠CAС1=180o
(2) ∠B1AB=∠C1AС — по условию
(3) ∠BAO1=90o-α
(4) ∠O1AС=∠CAO2=90o-βИз (1), (2), (3) и (4) получается, что:
2*∠C1AС+(90o-α)+(90o-β)=180o
2*∠C1AС+180o-α-β=180o
(5) ∠C1AС=(α+β)/2 - (6) ∠C1AС=∠C1AD+∠DAC=φ+∠DAC
(7) ∠DAC=∠O2CA=β — как внутренние разносторонние углы образованные двумя параллельными прямыми (AD) и (O2C) и секущей (AC)Из (5), (6) и (7) получается, что:
∠C1AС=φ+∠DAC
(α+β)/2=φ+β
φ+β=(α+β)/2
(8) φ=(α-β)/2 - k=tg (φ)=tg ((α-β)/2)
Из △ABO1:
sin (α)=[AO1]/[AB]
cos (α)=[BO1]/[AB]Из △ACO2:
sin (β)=[AO2]/[AC]
cos (β)=[CO2]/[AC]Под квадратными скобками подразумевается длинна отрезка (не хотел использовать вертикальные прямые — надеюсь, что читатель меня простит)
- Из предыдущего подпункта следует:

- Зная, что:
[BO1]=[CO2]=ΔX
[AO1]=YA-YB
[AO2]=YA-YC
[AB]=Sqrt ([AO1]2+[BO1]2)=Sqrt ((YA-YB)2+ΔX2)
[AC]=Sqrt ([AO2]2+[CO2]2)=Sqrt ((YA-YC)2+ΔX2)Получаем, что:

И так, k мы нашли; b мы тоже знаем (смотри выше), а значит прямая, на которой лежат опорные точки, нам известна.
Ищем опорные точки
Сразу скажу, что: ΔX'=Sqrt (ΔX2/(4+4*k2)), координаты опорной точки справа: XC1=XA+ΔX'; YC1=k*XC1+b, и слева: XB1=XA-ΔX'; YB1=k*XB1+b.


Из △AC1O:
ΔX'=[AC1]*cos (φ).
Если мы принимаем [AC1] равным половине шага по X между основным точками графика (точками B и A, A и C, т.д.), то: 
И вот, собственно:
XC1=XA+ΔX'
XB1=XA-ΔX'
YC1=k*XC1+b
YB1=k*XB1+b
К приятному!
- От товарища lany (огромное ему за это спасибо и плюс ему к карме) я узнал, что html5 с помощью функций quadraticCurveTo () и bezierCurveTo () умеет рисовать по canvas-у кривые Безье сам. Соответственно, алгоритм можно применить с JavaScript-ом.
- Приятной особенностью алгоритма есть то, что график предсказуемо «выпирает» за границы пространства точек, через которые мы собственно проводим график. Если брать расстояние до опорных точек равными половине шага по X (отрезок [AC1] на последнем рисунке), то зазора в четверть шага по X сверху и снизу от границ canvas-а будет достаточно.
Пример реализации на JSFiddle
