Игра Жизнь и Julia10.12.2022 17:47

В одной из своих прошлых статей по эволюции случайной конфигурации в игре жизнь я выдвинул гипотезу: Первая гипотеза касается окончания 'движухи' — в широком диапазоне изначальных плотностей p от 0.1 до 0.7, после окончания 'движухи' 'пепел' имеет одну и ту же плотность, около 0.27

Рассчитывая фрактал Римана, я был вынужден пересесть с Python на Julia из-за скорости, и не пожалел об этом. Однако теперь я мог на Julia быстро обрабатывать огромные конфигурации, например, 10k x 10k, и я решил повторить численные эксперименты на новом уровне. Как всегда, вас ждет и видео.

Впечатления новичка от языка Julia

Выбор Julia был скорее случаен — я искал язык, где имелась хорошая реализация zeta функции Римана. В Python эта реализация была в пакете чисел с произвольной точностью mpmath, и была очень медленной. В scipy функция не принимает комплексный аргумент и мне не подходит.

Язык Julia довольно редкий, поэтому я позволил себе описать впечатления новичка, который поработал с ним плотно лишь несколько дней.

Мне показалось, что Julia — это хороший выбор для математика, на Питоне быстро делаются модели, а когда мы упираемся в производительность то переписываем на Julia. Тем более он позволяет почти все, что есть в Питоне: и [] списки-массивы, и возврат многих значений из функции, и tuples, а функция:

function Sum(a,b)
  return a+b
end

отработает как в Питоне, для целых, вещественных, комплексных, и иных типов, которые можно складывать. (Для строк не отработает — строки в Julia складываются знаком умножения — почему?). То есть привычная нам утиная типизация, но в компилируемом языке. На самом деле Julia может 'подкомпилирывать' версии функции для разных типов параметров.

Тем не менее этим не надо заигрываться — оптимальный код в узких местах не должен содержать таких вещей.

Удивления на поверхности:

• Индексы массивов (по умолчанию) начинаются с 1. Но к этому быстро привыкаешь, как к левостороннему движению. Впрочем, может это было легко именно мне, потому что я родился в Англии начинал с Fortran IV.

• Как в математике, знак умножения можно опускать, 2b означает 2*b

• Считается хорошим тоном использовать unicode символы для кванторов, неравенства ⅀ ≟ ⊂ итд.

Макросы

Силой языка являются макросы, которые на самом деле являются программой, работающей с уже parsed syntax tree, а не со строками. Эти макросы могут полностью переписать ваш код. Да, код это тоже данные, потому что где-то в глубине живет наследие LISP.

Например, берем код генерации поля и перед ним добавляем Threads@threads- просим Julia вычислять цикл параллельно в разных threads:

function randomseed(prob, size, board)
  cellcnt=0
  Threads.@threads for y in 1:size
    r = rand(size)
    for x in 1:size
	  if r[x] < prob
	    board[x,y] = 1
        cellcnt[tid] += 1
	  end
    end
  end	
  return cellcnt
end

Вот и все! Правда, мы допустили ошибку: код выше правильно засеет поле, а вот значение cellcnt вычислит неверное, оно будет заниженным из-за неатомарности увеличения на единицу и коллизий. Не стоит делать это действие атомарным, лучше разделить потоки и потом сделать reduce, вот правильная версия:

function randomseed(prob, size, board)
  trd = Threads.nthreads()
  cellcnt=zeros(Int32, trd)
  Threads.@threads for y in 1:size
    tid = Threads.threadid()
    r = rand(size)
    for x in 1:size
	  if r[x] < prob
	    board[x,y] = 1
        cellcnt[tid] += 1
	  end
    end
  end	
  cellcntgbl = 0
  for i in 1:trd
    cellcntgbl += cellcnt[i]
  end
  return cellcntgbl
end

(у каждого треда свой счетчик, и потом они складываются)

Есть макросы turbo и simd — попытаться распарралелить цикл с помощью векторных инструкций. Они тоже попытаюсь переписать вашу программу, но я этого не пробовал.

Распознавание фигур в игре Жизнь

Мне хотелось считать количество разных фигур на поле, и делать это эффективно, за один проход и в многих тредах. Я ограничился фигурами не более 6×6:

Код детекции фигур на Julia выглядит безумно, но он очень эффективен (часть кода):

	  m64 = (((((s[1]<<6)+s[2])<<6)+s[3])<<6)+s[4] # 6 bit wide
	  m65 = (m64<<6)+s[5]
	  m66 = (m65<<6)+s[6]
	  m53 = ((((s[1]&31)<<5)+(s[2]&31))<<5)+(s[3]&31) # 5 bit wide
	  m54 = (m53<<5)+(s[4]&31)
	  m55 = (m54<<5)+(s[5]&31)
	  m56 = (m55<<5)+(s[6]&31)
	  m44 = ((((((s[1]&15)<<4)+(s[2]&15))<<4)+(s[3]&15))<<4)+(s[4]&15) # 4 bit wide
	  m45 = (m44<<4)+(s[5]&15)
	  m46 = (m45<<4)+(s[6]&15)
	  m35=  ((((((((s[1]&7)<<3)+(s[2]&7))<<3)+(s[3]&7)))<<3)+(s[4]&7))+(s[5]&7)

# now we can compare the rest of the slider
  if (m44 == 1632) cnt_block[tid] += 1 end
  if (m65 in (3220224, 4532352)) cnt_hive[tid] += 1 end
  if (m66 in (206086400, 69804800, 206127616, 139535104)) cnt_loaf[tid] += 1 end
  if (m55 in (403584, 141696, 206976, 141504)) cnt_boat[tid] += 1 end
  if (m55 == 141440) cnt_tub[tid] += 1 end
  if (m53 in (448, 1168)) cnt_blinker[tid] += 1 end
  if (m64 in (59136, 115584, 288288, 157248)) cnt_toad[tid] +=1 end
  if (m66 in (71901696, 139010304, 205529856, 201917184)) cnt_toad[tid] +=1 end
  if (m66 in (408969600, 102336000)) cnt_beacon[tid] +=1 end
  if (m55 in (75968, 206912, 272768, 403712, 460928, 467072, 133568, 139712, 268672, 399616, 78016, 208960, 137536, 143680, 333952, 340096))
    cnt_glider[tid] += 1 

По полю едут 6 слайдеров s, в которых хранятся 6 последних бит. Содержимое слайдеров переупаковывается в 'окна' m разной формы. Когда окно находится точно правее фигуры, значение m становится равным магическому числу. Для фигур типа block значение только одно, другие фигуры могут быть по-разному ориентированы и иметь разные фазы (например, как у глайдера).

Сами магические числа генерировались вспомогательной программой на Питоне.

Видео

Для матрицы 10k * 10k (тор, верх склеен с низом и правый край с левым) с начальной плотностью 30% и 3% прослеживалась эволюция на 15000 шагов. Цвет пикселя формировался по плотности мертвой материи:

• Синий — мертвая материя — blocks, blinkers

• Зеленый — активная жизнь

• Красный — глайдеры

• Так как поле 10k * 10k сжималось в 10 раз по каждой оси, каждый пиксель может иметь разную яркость и комбинации цветов (голубой — смесь живой и неживой материи)

Вот видео

Графики

Вначале посмотрим эволюцию при различной начальной плотности:

Как видно, действительно, при широком диапазоне начальных условий итоговая плотность получается одинаковой, однако это верно лишь для начальной плотности не менее 9%

Насколько важно брать большой размер поля?

Сравним результаты для квадратных полей разного размера для плотности 6%:

При большом поле графики более гладкие, что особенно видно по графику плотности глайдеров:

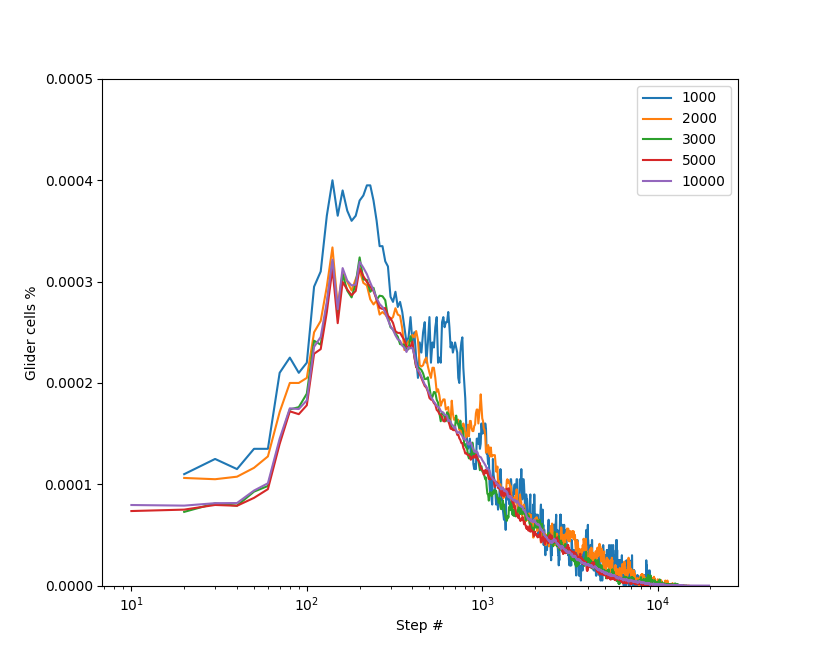
Кстати, обратите внимание на всплеск плотности в районе 130 — 250-го шага, действительно, при малых начальных плотностях конфигурации массово порождают глайдеры:

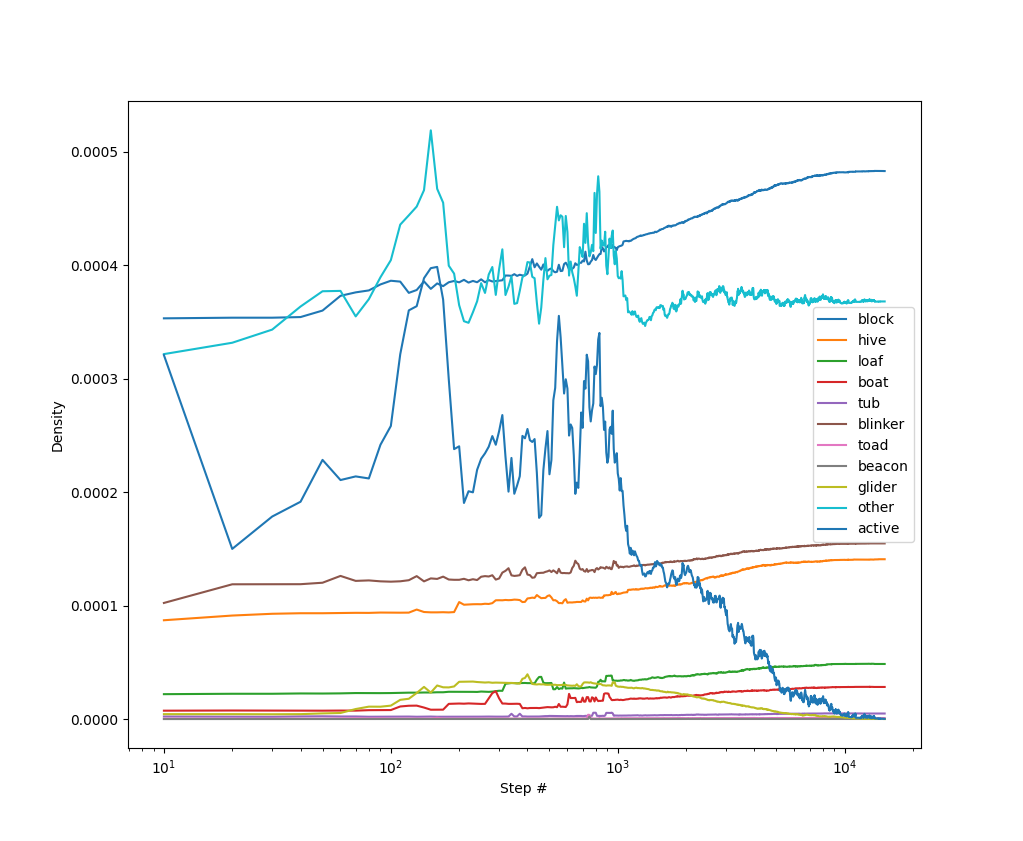
Концентрация клеток, принадлежащих разным фигурам:

Для начальной плотности 6%:

Для начальной плотности 30%:

Performance

Для поля 10k*10k один шаг занимает на моем AMD Ryzen 5 3600×6-Core Processor 3.79 GHz:

© Habrahabr.ru