Google Web Mercator: неоднозначная система координат
Первого октября 2014 года американское Национальное Агентство Геопространственной Разведки (NGA) опубликовало отчет, в котором изложена критика системы координат Web Mercator, используемой во множестве картографических веб-сервисов. К документу прилагалось подробное разъяснение проблемы и рекомендации для партнеров NGA. Документ получил большой резонанс, но далеко не все статьи, основанные на этом отчете, отличались точностью и грамотностью изложения. Это касается, например, статьи на сайте ГИС Ассоциации, которую, по причине грубейших ошибок в терминологии, можно считать безграмотной. Поскольку именно с этой системой координат разработчики веб-сервисов сталкиваются чаще всего, я считаю, что есть смысл разобраться в проблеме.О чем речь?
Для начала — пара определений, без которых некоторые детали не могут быть ясны. Важно понимать, что Web Mercator — это система координат, а не только проекция, хотя ее название и напоминает известную многим проекцию Меркатора. Именно это терминологическое разночтение вводит в заблуждение читателей статьи на сайте ГИС Ассоциации. Разница между проекцией и системой координат состоит в том, что проекция — это только способ, которым сложная форма модели фигуры Земли разворачивается на плоскость, тогда как система координат включает в себя также математическое определение модели (эллипсоида или сфероида), аппроксимирующей сложную фигуру Земли.
 На этой иллюстрации красным отмечено то, что относится только к механизму проекции (в данном случае — цилиндрической). К системе координат же относится вообще все, что здесь изображено.
На этой иллюстрации красным отмечено то, что относится только к механизму проекции (в данном случае — цилиндрической). К системе координат же относится вообще все, что здесь изображено.
В свою очередь, именно эта самая аппроксимирующая модель поверхности (пунктирная сфера на рисунке выше, на которой определены координаты λ, φ) и является источником проблемы, о которой дальше пойдет речь.
История
Я не могу сказать достоверно, кому первому и когда все это пришло в голову. Но, на сколько мне известно, первым крупным проектом, который стал использовать систему координат Web Mercator, был сервис Google Maps, и случилось это в 2005 году. Перед разработчиками стояла тогда задача упростить вычисления, необходимые для работы с картографическими данными, и самое очевидное, что можно было сделать — это использовать в системе координат сферу вместо эллипсоида. Занятно, что сам Герард Меркатор, скорее всего, исходил из таких же геометрических представлений, создавая свой способ проецирования карт на плоскость, потому что только Ньютон, живший несколько позже, предложил гипотезу о том, что Земля из-за центробежной силы имеет форму эллипсоида вращения, а не шара. Таким образом, разработчики Google, в каком-то смысле, вернулись в шестнадцатый век.
Критика в адрес этого подхода в профессиональных кругах звучит уже не в первый раз. Начиная с 2005 года, организация European Petroleum Survey Group (EPSG), занимающаяся стандартизацией в области систем координат и являющаяся держателем реестра их идентификаторов — кодов EPSG — отказывалась присвоить системе Web Mercator свой собственный официальный код, мотивируя это ее заведомым геометрическим несовершенством. Потому в сети можно встретить ссылки на эту систему через неофициальные коды: EPSG:900913, EPSG:102113 и другие. Однако, в 2008 году этой организации пришлось сдаться и присвоить код, так как популярность системы выросла, и ее нужно было как-то однозначно обозначать, чтобы не породить еще большую анархию. Первая попытка дать определение системе была не совсем удачной, но в конце концов ей был присвоен официальный SRID EPSG:3857.
Алгебра
Поскольку проекции — предмет изучения математики, я начну с формул, а потом дам им графическую иллюстрацию. Строго говоря, не обязательно даже хорошо владеть тригонометрией, чтобы понять разницу между реализацией систем координат на основе проекции Меркатора, сферы в одном случае и эллипсоида — в другом. Формулы заметно различаются внешне.Проекция Меркатора эллипсоида на плоскость задается следующим образом:
x=a×λy=a×ln[tan (π/4+φ/2)×((1-e×sinφ)/(1+e×sinφ))^(e/2)]
где: x и y — прямоугольные координаты, λ — долгота на эллипсоиде в радианах, φ — широта на эллипсоиде в радианах, a — значение большой полуоси эллипсоида, e — значение эксцентриситета эллипсоида (отношения большой и малой полуосей).
Если же вместо эллипсоида используется сфера, как это происходит в системе координат Web Mercator, все становится существенно проще, так как формула для ординат (оси Y) вырождается, давая следующее:
x=a×λy=a×ln[tan (π/4+φ/2)]
Согласитесь, выглядит куда проще и короче, чего и добивались разработчики Google. Это позволяет довольно заметно сократить количество математических операций при работе с картографическими материалами в клиентских и серверных приложениях.
Геометрия и картография
Даже если вообще не вдаваться в формулы, простые иллюстрации неплохо демонстрируют суть проблемы. Поясню сначала, что принцип построения проекции Меркатора состоит в том, что любая точка поверхности эллипсоида или сфероида проецируется на цилиндр, внутрь которого этот эллипсоид помещен так, чтобы их вертикальные оси совпадали, а поверхности либо касались по одной линии (наиболее частый случай), либо пересекались по двум. (Смотрите иллюстрацию выше). Далее, условные лучи проекции выходят из центра эллипсоида, пересекают его поверхность в точке P и попадают на поверхность цилиндра в точке P', куда и переносится соответствующая точка поверхности Земли. Легко мысленно представить себе, что если реальная поверхность Земли при этом сначала спроецирована не на довольно близкий к ее форме эллипсоид, а на идеализированную сферу, то при проекции на цилиндр точек сферы, одни и те же исходные точки земной поверхности окажутся на ином расстоянии от линии экватора по вертикальной оси, чем в случае с эллипсоидом.
Попробую проиллюстрировать «масштабы бедствия». Возьмем в архиве NASA EOSDIS спутниковый снимок в естественных цветах Центрального Федерального округа России, сделанный аппаратом MODIS Aqua с разрешением 250 метров на пиксель 21 сентября 2014 года (именно этот день — потому что он был ясным, так будет красивее) — это будет наш фон.
Далее, запросом через Overpass Turbo выгрузим из базы OpenStreetMap административные границы Московской области в формате GeoJSON. Код запроса:
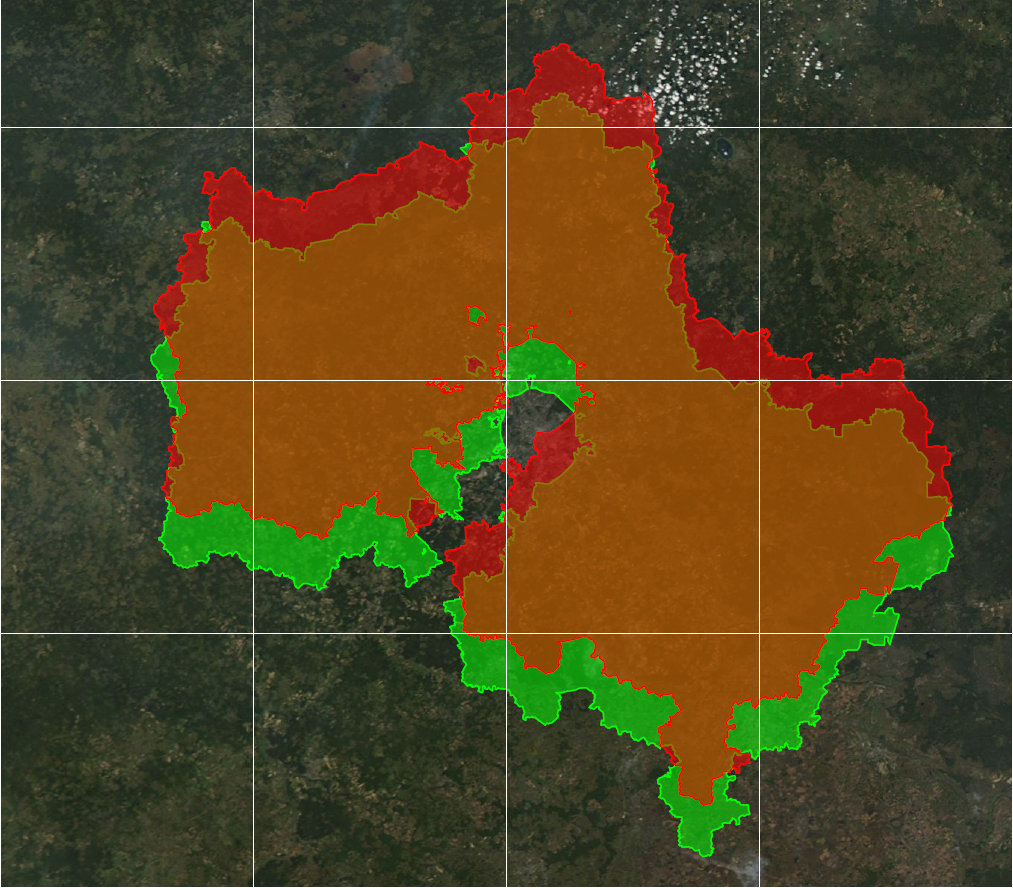
Зеленый контур на карте находится там, где нужно, а красный — сдвинут. Величина этого сдвига — 19,6 километров. Это не значит, что такая ошибка существует во всех картографических сервисах, использующих эту систему координат, вовсе нет. Но она проявится в случае, если взять данные в этой системе и попытаться совместить с другими данными без ее верного учета. В этом случае, к ней будет применено неверное обратное преобразование в географические координаты, что и приведет к ошибке.
Навигация
Некоторые картографические проекции обладают особыми свойствами, которые критичны для решения навигационных задач. Проекция Меркатора входит в их число, потому что ее широко используют для создания морских и аэронавигационных карт. Это возможно благодаря такому геометрическому свойству этой проекции, как конформность. В данном случае, оно означает, что форма объектов достаточно большого размера на этой карте сохраняется, так как сохраняются величины углов между линиями. Для навигации это означает, что глядя на карту, можно вычислить направление на искомую точку относительно меридиана (направления на географический север) и, двигаясь в этом направлении по магнитному компасу или под постоянным углом к линии на Полярную звезду, оказаться в нужном месте. Такой путь называется «локсодрома» и не является кратчайшим путем между двумя точками на поверхности Земли, а современные навигационные устройства позволяют вычислять путь по «ортодроме» — действительно кратчайшей линии, но от проекции Меркатора не отказываются, потому что карта, выполненная в ней, дает возможность в экстренной ситуации использовать для навигации подручные средства, не полагаясь на GPS-приемник и прочую электронику.
И вот здесь система координат Web Mercator оказывается обманчивой. Хотя она и основана на проекции Меркатора, но использование сферы с постоянным радиусом, как предельного упрощения модели поверхности Земли, лишает ее свойства конформности. Это значит, что двигаясь с постоянным курсовым углом, измеренным по такой карте, не удастся попасть в искомую точку из-за искажений углов в этой системе координат. Казалось бы, это не так важно для веб-сервисов, потому что по ним никто в своем уме не будет прокладывать путь в экстренной ситуации. Однако, разнообразие веб-сервисов велико, и гарантировать, что кто-то из разработчиков не вздумает считать какие-то направления в этой проекции — нельзя. При вычислениях в этой проекции ошибка может очень сильно накапливаться. Плюс, сейчас весьма популярны средства вроде САС.Планета, выкачивающие данные из веб-сервисов, и никто не может предугадать, что дальше с этими данным сделает пользователь.
Масштабы проблемы в данном случае тоже довольно легко измерить. Возьмем тот же снимок для фона, те же данные о положении административной границы Московской области. Теперь нам нужны три линии: ортодрома (кратчайшая с учетом кривизны Земли) и две локсодромы, построенные в системах Mercator/WGS84 и Web Mercator. Строить эти линии будем между самой южной точкой в Серебрянопрудском районе области, недалеко от населенного пункта с занятным названием «Мочилы» и самой северной — в Талдомском районе.
Построим ортодрому. Теперь измерим ее длину (получилось чуть меньше трехсот семи километров) и начальный угол относительно меридиана. Дальше — самое интересное. Перепроецируем рабочее пространство в проекцию Меркатора и построим из той же начальной исходной точки прямую в этой проекции линию, задав измеренный угол и длину 307 километров, не глядя, куда она попадет другим концом. Повторим то же самое, но в системе координат Web Mercator. Две локсодромы готовы. Для наглядности еще найдем на ортодроме центральную точку, поделив ее пополам и поставив в этом месте маркер. Перепроецируем рабочее пространство в UTM 37N WGS84, чтобы добиться минимального искажения углов, пропорций и прочих свойств карты.
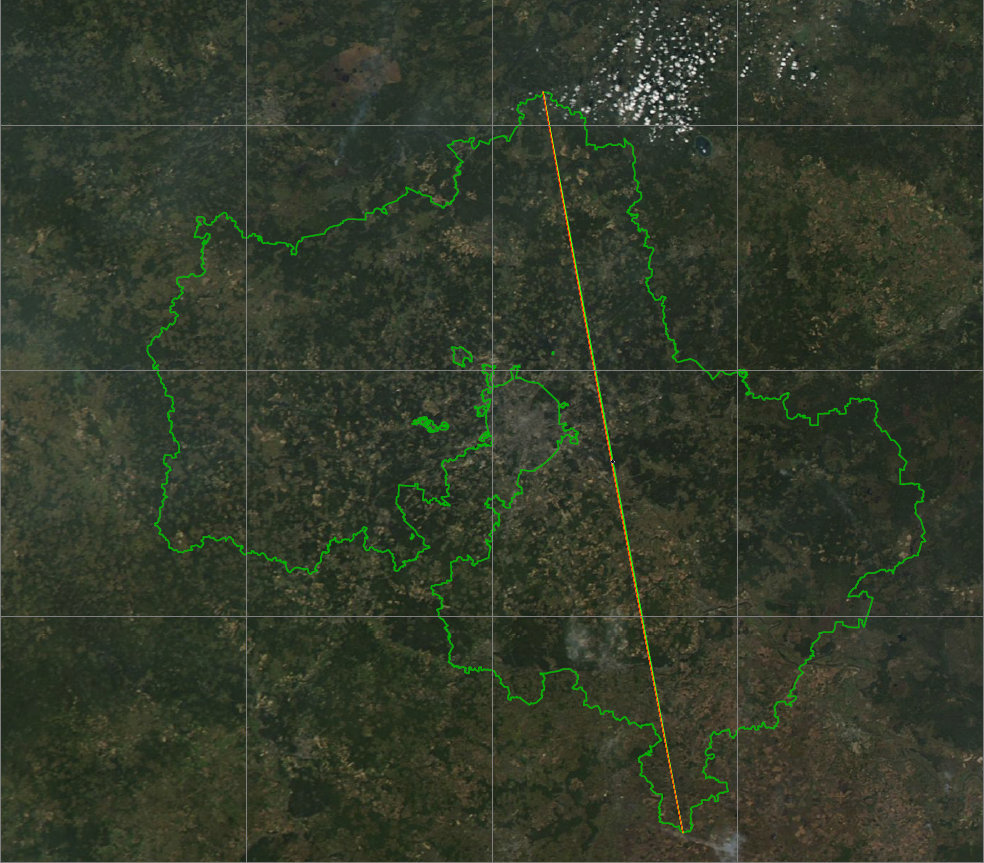
В таком масштабе почти ничего нельзя разобрать — все линии практически сливаются. Но взглянем поближе на центр линий, включив предварительно сетку с шагом 100 метров.
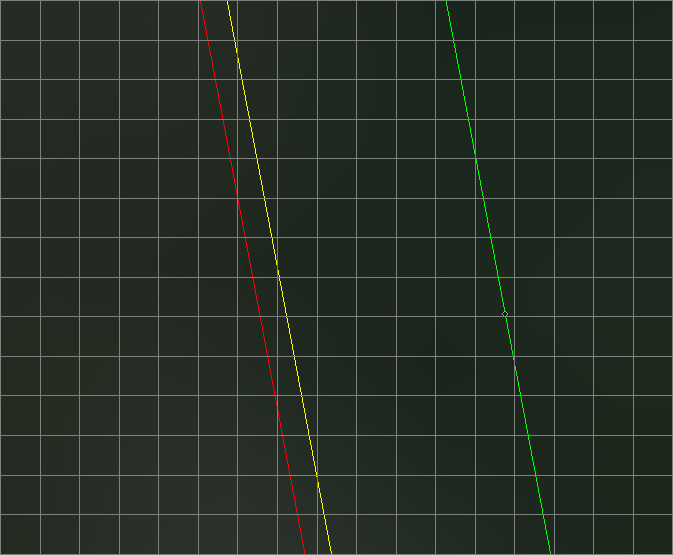
Зеленая линия с черной точкой на карте — это ортодрома. Желтая — локсодрома, которая построена в Mercator/WGS84, красная — локсодрома в Web Mercator. Как и ожидалось, локсодромы ушли от ортодромы, потому что они не являются кратчайшими расстояниями и относительно прямой ортодромы являются дугами. Основательно ушли — более чем на 500 метров. Но куда же они нас привели?

Желтая локсодрома, построенная в проекции Меркатора эллипсоида WGS84, описав правильную дугу, «волшебным образом» вернулась к нужной точке. Это означает, что в данной проекции можно попасть в нужную точку, зная начальный курсовой угол и двигаясь все время под этим углом к направлению на географический север. А с красной так не вышло — она промахнулась более чем на полторы сотни метров. Полторы сотни на три сотни тысяч метров пути. Четыре сотых доли процента. Много это, или мало? Это достаточно, чтобы не считать ее конформной и не использовать для вычислений, где это важно.
Имена, явки, пароли
Проблема с определением того, что используется система координат Web Mercator — не выдумана. Из-за ее, скажем так, «анархического» прошлого у нее столько имен, что все просто незвозможно перечислить. Однако, я попробую продемонстрировать, на сколько все ужасно, перечислив только некоторые из известных имен и кодов этой системы координат:
Web Mercator, Google Web Mercator, Spherical Mercator, WGS 84 Web Mercator, WGS 84/Pseudo-Mercator (при том, что «псевдо» тут как раз не Меркатор, а WGS84), WGS84 Web Mercator (Auxiliary Sphere), Popular Visualisation CRS / Mercator, WGS84 / Simple Mercator.
EPSG:900913, EPSG:3785, EPSG:3857, EPSG:102113, ESPG:102100, EPSG:41001, ESRI:54004.
Вот так эта система выглядит в формате PROJ.4:+proj=merc +lon_0=0 +k=1 +x_0=0 +y_0=0 +a=6378137 +b=6378137 +towgs84=0,0,0,0,0,0,0 +units=m +no_defsЗдесь следует обратить внимание на равные значения параметров размеров полуосей эллипсоида a и b. Их равенство и означает использование сферы. В случае, если это «честная» проекция Меркатора эллипсоида WGS84, она же EPSG:3395, в формате PROJ.4 она определяется вот так:+proj=merc +lon_0=0 +k=1 +x_0=0 +y_0=0 +ellps=WGS84 +datum=WGS84 +units=m +no_defsЛогика ситуации
Я не пытаюсь тут доказать, что система координат Web Mercator никуда не годится. Годится, конечно. И ровно тот же вывод (кроме вопросов, где важно соответствие военным стандартам США) можно обнаружить в отчете NGA. Просто важно понимать разницу между системами координат и их возможностями. Важно понимать, что Web Mercator используется почти везде: Google, OpenStreetMap, Bing, Yahoo и несчетное число других сервисов. Она также заложена в формат Slippy Map Tiles, в котором хранятся многие тайловые источники растровых данных. Она столь популярна, что далеко не все, кто ее используют, задумываются над тем, как же именно она устроена. А задуматься иногда стоит, особенно если планируемый сервис должен выполнять функции, более сложные чем простой показ картинки с картой.
Несколько занятных фактов вместо заключения
Агентство NGA, с отчета которого начался новый виток этой истории, до появления таких сервисов как NASA World Wind, Google Maps, Яндекс.Карты и других, было единственным доступным любому источником спутниковых снимков сравнительно высокого разрешения (10 метров на пиксель, черно-белое изображение) на территорию России, которые можно было бесплатно скачать через сервис NIMA Raster Roam (тогда NGA еще носило название NIMA — National Imagery and Mapping Agency). Эти снимки были частью разведывательной программы, выполнявшейся спутниками начиная с пятидесятых годов и попавшие в программу расскеречивания в 1995 году.
Сервис Яндекс.Карты не использует систему координат Web Mercator, он использует честную проекцию Меркатора эллипсоида WGS84, код EPSG:3395. С чем это связано изначально, мне неизвестно, но было бы весьма интересно услышать комментарии сотрудников Яндекса, которые здесь, на Хабре, присутствуют в немалом количестве.
Местные картографические сервисы скандинавских стран часто не используют проекцию Меркатора вообще, предпочитая те системы координат, которые приняты в этих странах, например, норвежский государственный сервис Norge i Bilder использует три зоны проекции UTM и датум EUREF89. Это вызвано тем, что в северных широтах проекция Меркатора дает слишком сильные деформации масштаба.
