Фракталы в иррациональных числах08.03.2019 06:19

Статья является продолжением моей первой статьи «Фракталы в простых числах».

un7du5h6vq5moklkm3jz4h7jgos.png

В предыдущей статье мы научились рисовать самоподобные паттерны с помощью взаимно простых чисел. В этой статье покажу фрактальную природу числа $\sqrt{2}$.
Без предисловия. Под кат.

Определимся с терминологией и обозначениями. В математике, описанные ниже системы называют бильярдами. Далее будем использовать этот термин. Размеры прямоугольного бильярда будем обозначать через $M$ (ширина) и $N$ (высота).

Двоичный бильярд.

В предыдущей статье мы брали прямоугольный бильярд со сторонами $M$ и $N$, запускали в него шар и отмечали траекторию пунктирной линией через клетку:

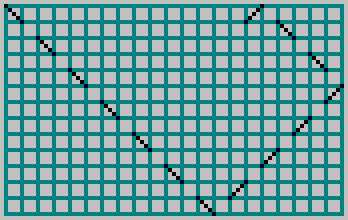
q8q1dmpklx695gzwf0m82uuvkxa.png

Для взаимно простых $M$ и $N$ получаем паттерн:

wmctlblg15sjbjbw1uxptzfiffi.png

В двоичной версии, траекторию отмечаем не пунктирной линией, а закрашивая поочередно клетки, черным и белым цветом (формируем двоичный массив, в соответствующую ячейку помещаем 0 для черного и 1 для белого):

z4lfj5_bk9qb12pmv0rcys3r2ia.png

Правила отражений на границах:

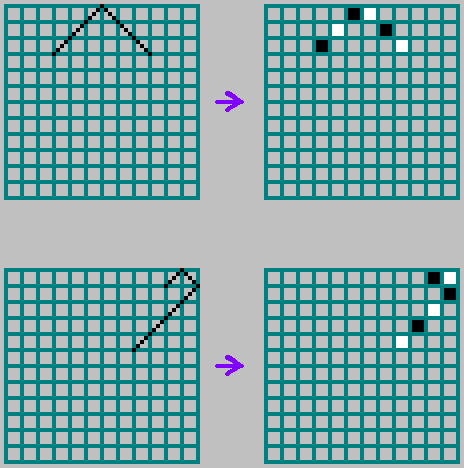
tlscfhguia7kbft-mvjxdxxivj4.png

Для взаимно простых $M$ и $N$ траектория проходит через каждую клетку:

-roqzus71qoc5z750waqbkft-kg.png

Для разных M и N

Если стороны имеют общий делитель — тогда шар попадает в угол до того, как пройдет через каждую клетку:

gdajgw1vexspkzo7lknlwf3oj20.png

Этот случай удобно рассматривать, как бильярд в прямоугольнике со сторонами $\frac{M}{НОД}$ и $\frac{N}{НОД}$ (НОД — наибольший общий делитель):

qd2brxygjy0p2vvxlwiomslpnhy.png

Прежде чем двигаться дальше, заполним таблицу предложенную пользователем Captain1312 в его статье (стороны бильярда будем делить на НОД).

$(1, 0)$ бит

Для каждого бильярда $M$ и $N$ возьмем бит с координатами $(1, 0)$.

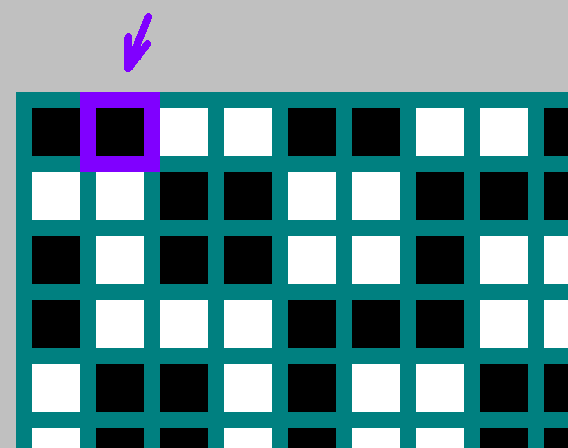
nyiiu_-dungqr-7l-bc7gk2odxc.png

Если $M$ является делителем $N$ — тогда бит с координатами $(1, 0)$ отсутствует ($\frac{M}{НОД}=1$). В этом случае берем инвертированный бит с координатами $(0, 1)$.

Заполняем таблицу. Начало координат — левый верхний угол. По $x$ — ширина бильярда $M$, по $y$ — высота $N$. Для каждого бильярда отмечаем бит $(1, 0)$, или инвертированный бит $(0, 1)$ (к этой теме вернемся ниже).

pjfjfsukgk2gnfqic5vj6pv_tca.png

Немного о числах Фибоначчи

Двоичная последовательность.

Почему мы инвертировали бит в тех случаях, когда ширина бильярда $M=1$? Для взаимно простых $M$ и $N$, траектория шара проходит через каждую клетку. Между верхней и левой стенкой бильярда, шар каждый раз проходит четное количество клеток.

vuxhvvfl7dj0uuo99bkd4xiabb8.png

zcme6cosjnmwn-wuojrh183ox6c.png

Биты в левом столбце — инвертированные биты из верхней строки. Нулевой бит не берем — с него начинается траектория:

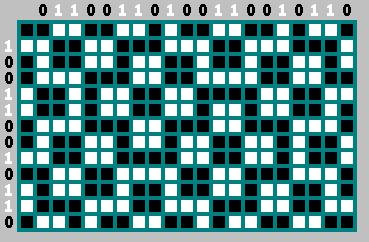
_giwh8sscush_rdxapv3r5-g9vi.png

Кроме того, мы можем смело выкинуть каждый второй бит из этой последовательности (бит $2_{n-1}$ — инвертированный бит $2_{n}$):

yltvc6hnnlxvpwwccwycg4jb2ng.png

Получили последовательность $1010010110$ для бильярда $(21,13)$. Последовательность уникальная для каждого $M$ и $N$.

Какую бы высоту $N$ мы не взяли — шар всегда проходит траекторию $2N$ между двумя отражениями от верхней стенки. От верхней стенки, движение всегда начинаем с »0» бита (черная клетка) и заканчиваем »1» битом (белая клетка):

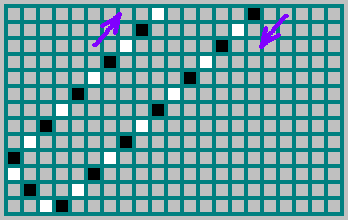
m0qujj7-k6gfgnvbymlx16i-m0a.png

Фактически, последовательность (которую мы выделили выше — $1010010110$) показывает, с какой стороны прилетел шар: 1 — если шар прилетел, отразившись от правой стенки и 0 — если шар прилетел, отразившись от левой стенки. На картинке траектория шара отмечена черным, если шар двигался вправо и белым — если двигался влево:

9tdedd_8hln5b5ehk4lipauz3aq.png

Это интересно
С помощью бильярда можно делить два числа в двоичной системе счисления. В момент касания верхней или нижней стенки фиксируем направление движения шара. Если шар двигался вправо — запишем 0. Если влево — запишем 1. Фиксировать будем каждое $2^n$ касание шара.
Первое касание нижней стенки. Шар двигался вправо. Зафиксировали 0
Второе касание — верхней стенки. Шар двигался влево. Зафиксировали 1
Четвертое касание — верхней стенки. Шар двигался вправо. Зафиксировали 0
Восьмое касание — верхней стенки. Шар двигался вправо. Зафиксировали 0
И т.д.
Получили: 0.1001111001111001111… — это двоичная запись дроби $\frac{13}{21}$.

rj6u4_q8rx1ixua8pqlxud97gi0.png

Эта последовательность ($1010010110$) содержит всю необходимую информацию о паттерне. С помощью нее мы можем восстановить исходный паттерн (и даже заглянуть за нижнюю границу паттерна). Возьмем квадрат со сторонами $M$. Расставим биты нашей последовательности в тех местах, в которых шар ударился об верхнюю стенку (расстояние между соседними касаниями шара — 2 клетки).

-xtmoqqdbu1ah2qpjx8t60tx-t4.png

Если соответсвующий бит = 1 — начинаем двигаться влево, отмечая траекторию через клетку. Если бит = 0 — двигаемся вправо.

ad3amwwfsbtw5-usbxxnxrqpdwa.png

При этом не забываем про нулевой бит:

740yz8ych-80fk0p_615wb0rqws.png

Gif:

zbqgegwot1zywuomdevkk2w7jzq.gif

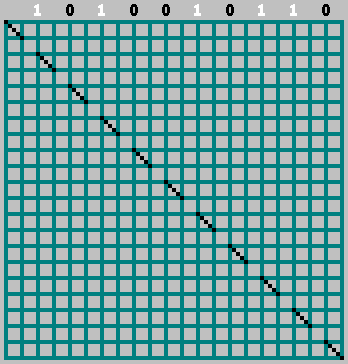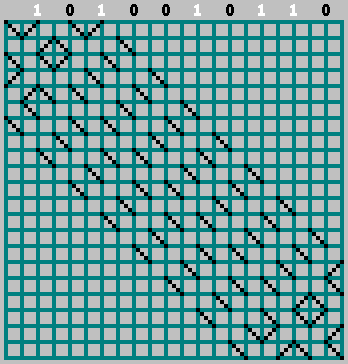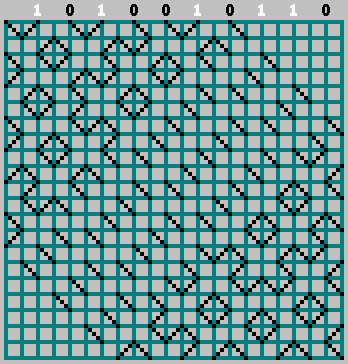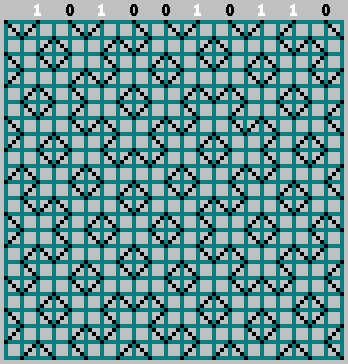
Получили исходный паттерн (и немного заглянули за нижнюю границу):

mlqx7aeqopsgt-g83if9sbc1us8.png

Скрипт для визуализации двоичных последовательностей

Эту последовательность мы можем построить с помощью остатков от деления.

Одномерный бильярд.

На числовой оси $X$ возьмем две точки: $0$ и $M$.

eynjtu819jtj84bntbovcxg7s68.png

Двигаясь от одной точки к другой, отмеряем расстояния $N$:

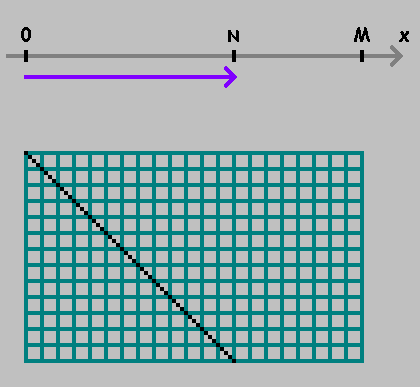
fmyiohaeo6bat1zlhlw3vfkkg3o.png

Отметили точку. Продолжаем отмерять расстояние от этой точки, сохраняя направление. Если достигли точки $0$ или $M$ — меняем направление:

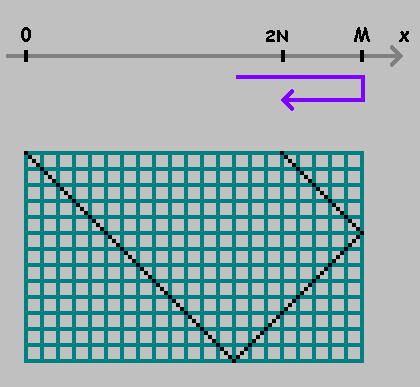
k7nlxadkkmf0tedy19a6mad2uzo.png

Как видно на рисунках выше, первая точка показывает место, где шар касается нижней стенки бильярда. Эта точка нас не интересует. Мы будем фиксировать только точки $2kN$ для $k=0,1,2,…$.

Как отметить эти точки? Развернем наш бильярд на оси $X$. Отметим точки $0, M, 2M, 3M,…$. Теперь достигнув точки $M$ мы не меняем направление движения, а продолжаем двигаться к точке $2M$.

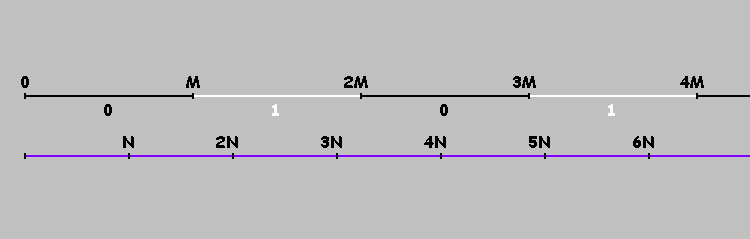
w36orai2_c0n1g6a5lcezjhaspo.png

Точки, кратные $M$, делят нашу ось на отрезки. Условно отметим эти отрезки единицами и нулями (чередуются). На отрезках, отмеченных нулями, шар (в прямоугольном бильярде) двигается слева направо. На отрезках, отмеченных единицами — справа налево. Или проще: шар двигается слева направо, если $Q_k=0$, для

$Q_k=\lfloor \frac{2kN}{M} \rfloor \; (\textrm{mod} \; 2); \quad k=0,1,2,…$


(На эту формулу следует обратить особое внимание. Далее мы к ней вернемся)

Легко заметить, что точка, в которой шар коснулся верхней стенки бильярда — это остаток от деления $2kN$ на $M$. При этом мы можем не фиксировать движение шара в обратную сторону. Берем целую часть от деления $2kN$ на $M$, если она четная — считаем остаток от деления $2kN$ на $M$. Получившийся остаток разделим на 2 (расстояние между соседними точками касания — две клетки). Получили индексы элементов массива, которые нам надо заполнить нулями. Оставшиеся элементы заполняем единицами (шар двигался от правой стенки к левой).

Длина последовательность = $\frac{M}{2}$.

function sequence(m,n){
        var md=m/2;
        var array=[];
        for(var k=0;k 0101001011010010110101101001

Теперь мы можем построить двоичную последовательность для бильярда с любыми сторонами $M$ и $N$ (натуральными числами).
Несколько примеров:
144×89 (числа Фибоначчи):
010100101101001011010110100101101001010010110100101101011010010110100101

169×70 (числа Пелля):
0101011010100101011010100101011010110101001010110101001010110101001010010101101010010

233×55 (нечетные числа Фибоначчи $F_n$ и $F_{n-3}$):
0100100110110110010011011011001001001101100100100110110010010011011011001001101101100
10010011011001001001101100100100

Еще одна интересная таблица
Очень любопытные графики получаются, если взять бильярд с шириной $M$ и построить последовательности для каждого $N$ от $0$ до $M$. Далее эти последовательности сложить стопкой.

        var array;
        for(var y=1;y

Несколько примеров.
M=610:

gev87fnksb-exn82mmrw33cardg.png

M=611:

_g9sizbwuclzm3zarfb_mgw3_ko.png

M=612:

lxml_s1gvaqionwjvym4gwymfkg.png

M=613:

uthckdx32-okvu7xg-ugpaewjee.png

M=614:

qwaymewmcxx1kpwromky_x3gtya.png

Для остальных M

Последовательности у нас есть. Как еще можно визуализировать двоичные последовательности? С помощью Черепашьей графики.

Turtle graphics.

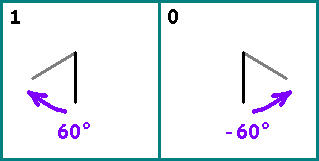
Рисуем отрезок. Далее берем поочередно биты из нашей последовательности. Если бит =1 — поворачиваем отрезок относительно предыдущего на $60^{\circ}$ (по часовой). Если бит = 0 — поворачиваем отрезок на $-60^{\circ}$. Начало следующего отрезка — конец предыдущего.

yn4xuzstc3jx6gbcmpffc5kkwbc.png

Возьмем два достаточно больших числа Фибоначчи: $F_{29}=514229$ и $F_{28}=317811$.
Построили последовательность:
00101101001011010010100101101001011010110100101101001010010110100101… (257114 символов плюс нулевой бит).
Визуализируем с помощью черепашьей графики. Размер начального отрезка — 10 пикселей (начальный отрезок в правом нижнем углу):

c6sk3iz4_ak5a-wk--ktnqsqhxc.png

Размер начального отрезка — 5 пикселей:

srkm_4mroo4llcwpv7y4rcsjjvi.png

Размер начального отрезка — 1 пиксель:

9yq6-jaclmxp7qavbiruxigtlr4.png

Следующий пример — числа Пелля.

$P_n=\begin{cases}0, n=0;\\1, n=1 \\2P_{n-1}+P_{n-2}, n>1 \end{cases}$» /></p><p> <br />Берем <img src= и $P_{15}=195025$.
Последовательность:
00101001010110101001010110101001010010101101010010101101010010101101 (235415 символов плюс нулевой бит).
Размер начального отрезка — 1 пиксель:

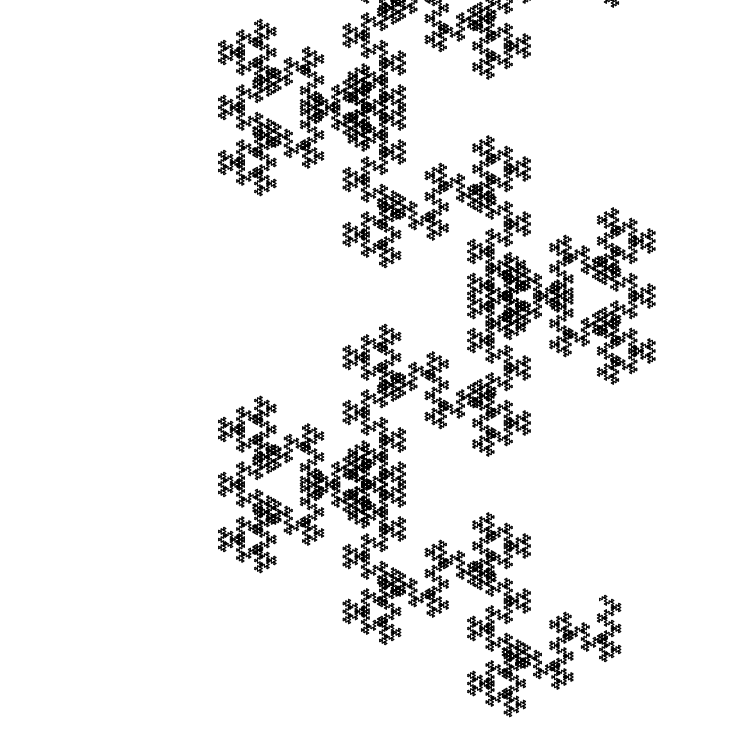
_6wkqdlsa3-anayzy9q0sg7nkxw.png

Еще один пример — нечетные числа Фибоначчи $F_n$ и $F_{n-3}$.
Берем $F_{28}=317811$ и $F_{25}=75025$.
Последовательность:
00110110010010011011001001001101101100100110110110010011011011001001… (158905 плюс нулевой бит).
Вместо углов $60^{\circ}$ и $-60^{\circ}$ будем использовать углы $90^{\circ}$ и $-90^{\circ}$.
Размер начального отрезка — 5 пикселей:

5n2cijgjxqfsvxnuklurcjrhxhq.png

Размер начального отрезка — 0.4 пикселя:

ucua-g5zkg0dt0kzahbiihtrgzy.png

У этой кривой есть название — «Fibonacci word fractal». Размерность Хаусдорфа для этой кривой известна:

$D=3{\frac {\log \Phi }{\log(1+{\sqrt {2}})}}=1,6379; \quad \Phi =\frac {1+{\sqrt {5}}}{2}$

Скрипт для визуализации двоичных последовательностей с помощью Turtle Graphics

Проблема.

Можно ли нарисовать паттерн для бильярда, стороны которого несоизмеримы (одна из сторон — иррациональное число)? Задача нетривиальная. Пытаясь решить эту задачу, мы столкнемся с рядом вопросов:
1. Если стороны несоизмеримы — мы не можем замостить бильярд клетками одинаковой величины.
2. Если стороны несоизмеримы — шар будет бесконечно отражаться и никогда не попадет в угол.
3. Последовательности в бильярдах заполняются не по порядку, а хаотично.

nhkqvy-hfv4gzpofzwldv-lzjby.gif

Первые два вопроса, очевидно, не имеют решения. Но если бы существовал способ заполнить последовательность по порядку — тогда мы могли бы, двигаясь по последовательности слева направо, восстановить паттерн способом, которым мы пользовались выше. И тем самым увидеть, как выглядит паттерн в левом верхнем углу бильярда, стороны которого несоизмеримы.

Черная магия.

Возьмем бильярд, стороны которого равны числам Фибоначчи (с другими числами такой фокус может не сработать). Запустим в него шар и будем фиксировать номер касания шара у верхней стенки. Номера закрасим белым цветом — если шар двигался справа налево и черным — если шар двигался слева направо:

-wudhtmq_g_hln8naiocxdnfrjo.png

Белому цвету соответствует единица в последовательности, черному — ноль. Теперь расставим номера по порядку:

zjbrbhdgnvljwmbst-vqfk1g9a4.png

Получили точно такую же последовательность единиц и нулей.

Для других чисел
Начало координат — левый верхний угол. По оси $x$ — ширина бильярда $M$. По оси $y$ — высота бильярда $N$. Белыми точками отмечены числа, для которых последовательности совпадают:

gtvpsvmohygmilbpdpjgiknj2l8.png

Числа, для которых последовательность инвертируется:

avtvia2u5toiylamwnrptbw99h0.png

Закинул скрипт:

y_auhqb9nma4xppu7dxrm269mik.png

Первая строка — координаты мышки, которые используются в качестве ширины и высоты бильярда.
Вторая строка — первые 100 бит последовательности, полученной через остатки от деления.
Третья строка — первые 100 бит последовательности, полученной через четность целой части.

Черный цвет — Визуализация первой последовательности с помощью Turtle graphics.
Фиолетовый — визуализация второй последовательности.

Фактически, в некоторых случаях, нам не надо брать остаток от деления. Для чисел Фибоначчи достаточно проверить четность целой части от деления $2kN$ на $M$:

$Q_k=\lfloor \frac{2kN}{M} \rfloor \; (\textrm{mod} \; 2); \quad k=0,1,2,…$

В числителе у нас $F_{n}$. В знаменателе — $F_{n+1}$.

Как известно:

$\lim_{n\to\infty} \frac{F_n}{F_{n+1}}= \frac{1}{\Phi}$

$\Phi$ — Золотое сечение. Иррациональное число. Теперь нашу формулу можем записать как:

$Q_k=\lfloor \frac{2k}{\Phi} \rfloor \; (\textrm{mod} \; 2); \quad k=0,1,2,…$

Получили формулу, с помощью которой можем по порядку заполнять последовательность для бильярда, ширина которого равна $\Phi$, а высота — $1$. Длина последовательности = $\infty$, но мы можем восстанавливать часть паттерна, двигаясь слева направо по последовательности и заглянуть в верхний левый угол бильярда. Осталось разобраться, как посчитать $\Phi$

Единицу деленную на золотое сечение можно переписать как:

$\frac{1}{\Phi}=\frac {-1+{\sqrt {5}}}{2}$

Мы можем избавиться от двойки:

$\frac{2k}{\Phi}=\frac {2k(-1+{\sqrt {5}})}{2}=k\sqrt{5}-k$

Наша формула принимает вид:

$Q_k=\lfloor k\sqrt{5}-k \rfloor \; (\textrm{mod} \; 2); \quad k=0,1,2,…$

Для наглядности нарисовал таблицу. В третьей колонке отбрасываем дробную часть и оставляем целую. В четвертой колонке проверяем четность целой части:

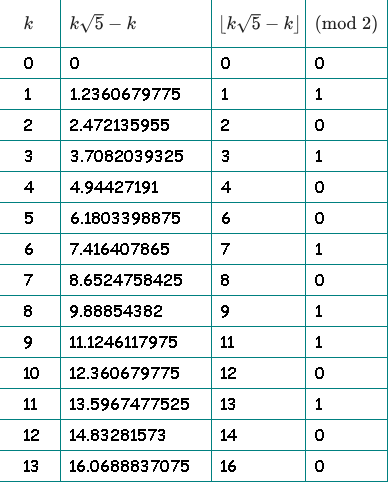
n0uwaujomthg9xpzxld8k2fwuv8.png

В четвертой колонке получили нашу последовательность: 01010010110100…

Продолжаем вычислять биты для остальных $k$. Восстанавливаем часть паттерна для бильярда со сторонами $1$ и $\Phi$:

blfn7nzfrczm2zdqx7gbvzptw5i.png

Если не отнимать каждый раз $k$ — тогда каждый второй бит в последовательности инвертируются. Получим общую формулу:

$Q_k=\lfloor k\sqrt{x} \rfloor \; (\textrm{mod} \; 2); \quad k=0,1,2,…$

Что нам мешает вместо квадратного корня из пяти использовать квадратный корень из трех или, скажем, из двух? Ничего.

Построим последовательность для $k\sqrt{3}+k$


var x=3;
var q=[];
for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x)+k)%2;

Первые несколько бит последовательности:
00100101101001001011010010110110100101101001001011010010010110100101…

Визуализировать будем с помощью черепашьей графики. Углы 90 и -90 градусов. Размер начального отрезка 5 пикселей:

pdav-t1daztjfyab_qkvgimjfie.png

Размер начального отрезка — 0.5 пикселя:

clgwx5_wieiquxz9knrae71cmfk.png

Построим последовательность для $k\sqrt{2}$


var x=2;
var q=[];
for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x))%2;

Первые несколько бит последовательности (A083035):
01001101100100110010011011001101100100110110011011001001100100110110…

Углы 90 и -90 градусов. Размер начального отрезка 5 пикселей:

hwwjv2_cuoworinwyptdj--jolo.png

Размер начального отрезка — 0.5 пикселя:

a7y1_lcngd3qbaix-4jteid9voe.png

Это интересно
Из этой кривой можно восстановить «бильярдный паттерн» и посмотреть, что находится вокруг кривой:

eodnzusaufkmtyuvanqt0yehh40.png

Интересно было бы подобрать $M$ и $N$ для этого паттерна.

И это
Количество отрезков в повторяющейся части кривой = $P_n$ (числа Пелля: 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, …).

lq0urbr0k67x3zhmax5vm1q-g7e.png

$\sqrt{2} = \lim_{n\to\infty} \tfrac{P_{n-1}+P_n}{P_n}$


Углы 60 и -60 градусов. Размер начального отрезка 5 пикселей:

cq286wzjeultcptbnzg4zsq5oey.png

Скрипт для визуализации

Кто-то может засомневаться в том, что четность целой части от $k\sqrt{2}$ дает фрактальную последовательность. Визуализируем часть этой последовательности вторым способом:

zhbg3pip_al1c6qqi_uikclquvc.png

Для наглядности, закрасил самую длинную кривую в получившемся паттерне:

6ozgcxqkvjmlu9qgmkbl8ups32q.png

У этой кривой есть название — «Fibonacci word fractal».

Как с помощью бильярда получить эту последовательность? Берем бильярд, ширина которого = 1, а высота = $\sqrt{2}$. У верхней и нижней границы фиксируем направление движения шара. Если шар двигался слева направо — записываем 0, если справа налево — записываем 1.

9pkwezrmqwgbnigz1i76legoqh8.png

Два графика:

$z=\lfloor y\sqrt{x} \rfloor \; (\textrm{mod} \; 2)$

iiigqffblpoldf25kiwkmipgh9e.png

$z=\lfloor yx\sqrt{2} \rfloor \; (\textrm{mod} \; 2)$

lsdlhf91evl86ygryw1p3cwol8i.png

Продолжать в том же духе можно очень долго — у паттернов есть много интересных свойств. Но статья и без того получилась слишком громоздкой. Об одном из интересных свойств расскажу напоследок.

В двоичном бильярде мы запускали шар из левого верхнего угла и заполняли матрицу битами.

Для бильярда 610×377:

7muai0_k5f3cweqfvea0df1oz_w.png

Увеличенная часть паттерна:

z_xzuar26aqmf4csdrbpm7sib0w.png

Если запустить второй шар из другого угла (из левого нижнего для бильярда 610×377) и отметить биты, которые совпадают для обеих траекторий — получим очень любопытный паттерн:

6luwbdiavnyurynf2gnvcomklbs.png

Совпадающие биты отмечены черными пикселями. Увеличенная часть паттерна:

4dfkuzvcswyhjxbfdujjkl8wnee.png

Существует еще два способа нарисовать этот паттерн. Об одном из них упомянул в статье Perfect shuffle. Второй:

Нарисуем график функции:

$z=\sin(x\pi(\sqrt{5}+1))+\sin(y\pi(\sqrt{5}+1))$

И отметим черными точками $z<0$:

twx0oxrtmyuzb7fy8ajgbfstu80.png

Увеличенная часть паттерна:

1cjebdf71w0-bwt7lowz7lijmpq.png

© Habrahabr.ru