FlashSort – метод сортировки данных за линейное количество перестановок
Привет всем!
У меня есть одно хобби — я очень люблю изобретать велосипеды.
Об изобретении одного такого велосипеда хочу вам сегодня рассказать.
Сортировка массива данных — задача, которой далеко уже не первый год. Она преследует нас с первых курсов технических вузов, а кому особенно повезло, то и со школьной скамьи. Обычно это методы сортировки «пузырьком», «делением», «быстрая», «вставками» и прочие.

Вот, к примеру, подобной реализации метода сортировки «пузырьком» меня учили в одной крупной IT-компании. Этот метод использовался матёрыми программистами там повсеместно.
Так вот, мне всегда было интересно, почему уделяется так мало внимания методам сортировки без сравнения (поразрядная, блочная и т.п.). Ведь подобные методы относятся к классу быстрых алгоритмов, выполняются за О (N) количество перестановок и при удачно подобранных данных могут выполняться за линейное время. Для сортировки каких-то абстрактных объектов они, конечно, слабо подходят, поскольку эти методы, собственно, ничего и не сравнивают, а берут какой-то разряд от значения (хотя при особом желании можно вкорячить и сортировку объектов). Однако на практике большинство задач сортировки сводятся к упорядочиванию массива обычных примитивов: строк, чисел, битовых полей и пр., где сравнение проходит в основном побайтно.
Если, к примеру, мы будем говорить о методе карманной сортировки, то Википедия утверждает, что он плохо работает при большом количестве малоотличных элементов или же на неудачной функции получения номера корзины по содержимому элемента. Алгоритм требует заведомо знать природу сортируемых данных. Также дополнительно требуется организовать карманы, что отъедает процессорное время и память. Однако, несмотря на все недостатки, потенциально время выполнения алгоритма в теории стремится к линейному. Возможно ли как-то решить указанные недостатки и добиться линейного времени выполнения?
Итак, предлагаю вашему вниманию алгоритм сортировки с O (N) количеством перестановок и со временем выполнения «близкому» к линейному.
Алгоритм сортирует исходные данные по-месту и не использует дополнительной памяти. Иначе говоря, сортировка с О (N) перемещениями и памятью O (1).
Метод сортировки основан на методе карманной сортировки. Если говорить о конкретной реализации, то для более эффективного сравнения элементов побайтно количество карманов выбрано равным 256. Количество итераций (проходов) зависит от длины одного элемента в байтах. Т.е. общее количество перестановок будет равно О (N*K), где K — длина (количество байт) одного элемента.
Для сортировки нам необходимо использовать специальный буфер — «карманы». Это массив длиной 256, каждый элемент которого содержит размер кармана и ссылку на границу кармана — это указатель на первый элемент кармана в исходном массиве. Изначально буфер проинициализирован нулями.
Итак, алгоритм сортировки для каждой i-й итерации состоит из четырех этапов.
1 этап. Подсчет размера карманов
На первом этапе рассчитываются размеры карманов. Мы используем наш буфер, где для каждого кармана будет вестись счетчик количества элементов. Мы пробегаемся по всем элементам, берем значение i-го байта и инкрементируем для соответствующего кармана счетчик.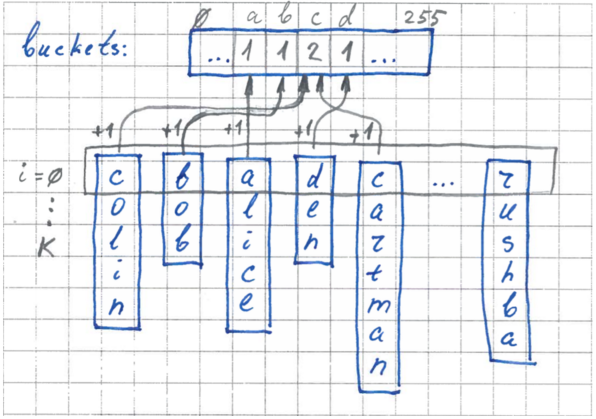
2 этап. Расстановка границ
Теперь, зная размеры каждого кармана, мы можем четко расставить границы в нашем исходном массиве для каждого кармана. Мы пробегаемся по нашему буферу и расставляем границы — устанавливаем указатели на элементы для каждого кармана.
3 этап. Перестановка
Вторым проходом мы переставляем элементы в исходном массиве таким образом, чтобы каждый из них оказался на своем месте, в своем кармане.
Алгоритм перестановки следующий:
- Пробегаемся по порядку по всем элементам массива. Для текущего элемента берем его i-й байт.
- Если текущий элемент на своем месте (в своем кармане), то всё ОК — передвигаемся дальше, к следующему элементу.
- Если элемент не на своем месте — соответствующий ему карман находится дальше, то производим перестановку с тем элементом, который находится в этом дальнем кармане. Повторяем эту процедуру до тех пор, пока нам не попадется подходящий элемент с нужным карманом. Каждый раз, производя замену, мы кладем текущий элемент в свой карман и повторно уже не анализируем. Таким образом, количество перестановок никогда не будет превышать N.
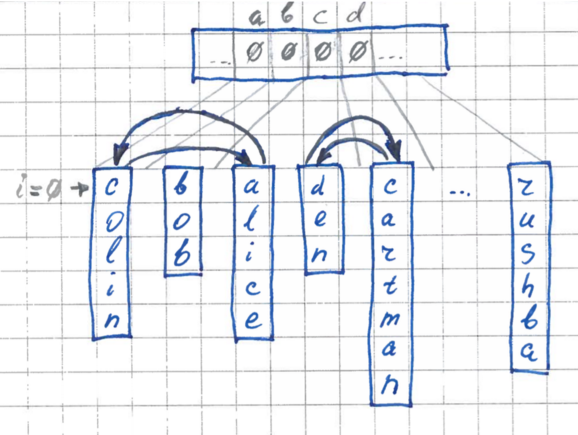
Во время каждой перестановки счетчики в буфере для соответствующего кармана будут обратно декрементироваться, и к концу пробега наш буфер будет снова заполнен нулями и готов к использованию на других итерациях.
Процесс перестановки, как и первый этап, теоретически будет выполняться за линейное время, поскольку количество перестановок никогда не будет превышать N — количество элементов.
4 этап. Рекурсивный спуск
И последний этап. Теперь мы рекурсивно сортируем элементы внутри каждого сформированного кармана. Для каждой внутренней итерации необходимо лишь знать границу текущего кармана. Поскольку мы не используем дополнительной памяти (информации о длине текущего кармана у нас нигде не сохранилась), мы, перед тем как перейти к внутренней итерации, снова пробегаемся по элементам и вычисляем длину текущего кармана.

При желании этого можно избежать, дополнительно оптимизировав алгоритм и не удаляя информацию о длинах карманов. Однако это потребует использования дополнительной памяти. В частности O (log (K) * M), где M — количество карманов (в нашем случае это всегда 256), K — длина одного элемента (в байтах).
Отличительной особенностью алгоритма является то, что при первом проходе (этап №1) дополнительно запоминается номер первого и последнего не пустого кармана (указатели pBucketLow, pBucketHigh). В дальнейшем это позволит сэкономить время на 2-м и 3-м этапах. Подобная оптимизация предполагает, что большинство данных сосредоточено в определенном диапазоне данных и часто имеет некоторые заданные границы. Например, строковые данные часто начинаются с символа A-Z. Числа (например ID) также обычно ограничены каким-то диапазоном.
Дополнительную оптимизацию можно провести также и в случае, если номера нижнего и верхнего не пустого кармана совпадают (pBucketLow == pBucketHigh). Это говорит о том, что все элементы на i-м уровне имеют одинаковый байт, и все элементы попадают в один карман. В этом случае мы можем тут же прервать итерацию (пропустить 2,3,4 этапы) и перейти к следующей.
В алгоритме также используется еще одна достаточно распространенная оптимизация. Перед началом выполнения любой итерации, в случае когда количество элементов невелико (в частности, меньше 8), оптимальнее проводить какую-нибудь очень простую сортировку (например, bubble-sort).
Реализация
С реализацией вышепредставленного алгоритма на языке Си можно ознакомиться на github: github.com/denisskin/flashsort
Для сортировки данных нужно воспользоваться функцией flash_sort, которая в качестве параметра принимает указатель на функцию get_byte (void*, int) — функцию получения i-го байта элемента.
Например, сортируем строки:
// sort array of strings
char *names[10] = {
"Hunter",
"Isaac",
"Christopher",
"Bob",
"Faith",
"Alice",
"Gabriel",
"Denis",
"****",
"Ethan",
};
static const char* get_char(const void *value, unsigned pos) {
return *((char*)value + pos)? (char*)value + pos : NULL;
}
flashsort((void**)names, 10, get_char);
Также в распоряжении имеется функция flashsort_const для сортировки данных строго заданной длины.
Например, чисел:
// sort integer values
int nums[10] = {9, 6, 7, 0, 3, 1, 3, 2, 5, 8};
flashsort_const(nums, 10, sizeof(int), sizeof(int));
Эту же функцию можно с успехом использовать и для сортировки массива структур по ключу.
Например:
// sort key-value array by key
typedef struct {
int key;
char *value;
} KeyValue;
KeyValue names[10] = {
{8, "Hunter"},
{9, "Isaac"},
{3, "Christopher"},
{2, "Bob"},
{6, "Faith"},
{1, "Alice"},
{7, "Gabriel"},
{4, "Denis"},
{0, "none"},
{5, "Ethan"},
};
flashsort_const(names, 10, sizeof(KeyValue), sizeof(names->key));
Функция flashsort_const по понятным причинам будет работать чуть медленнее ее аналога — функции, которая была объявлена при помощи специального макроса. В этом случае перестановка элементов и получение i-го байта элемента будет происходить значительно быстрее.
Например, объявить функцию сортировки чисел при помощи макроса можно следующим образом:
// define function flashsort_int by macro
#define FLASH_SORT_NAME flashsort_int
#define FLASH_SORT_TYPE int
#include "src/flashsort_macro.h"
int A[10] = {9, 6, 7, 0, 3, 1, 3, 2, 5, 8};
flashsort_int(A, 10);
Бенчмарки
В этом же репозитории можно найти и бенчмарки, где для сравнения добавлена сортировка методом qsort.
cd benchmarks
gcc ../src/*.c benchmarks.c -o benchmarks.o && ./benchmarks.o
В результате, метод flash_sort хорошо показывает себя по сравнению с qsort в работе со случайно распределенными данными. Например, сортировка массива из 500К чисел типа int работает в 2.5 раза быстрее quick-sort. Как видно из бенчмарка, среднее время сортировки, деленное на N, с ростом количества элементов практически не меняется.
Benchmarks sorting of integers
-------------------------------------------------------------------------------------------
Count Flash-sort | Quick-sort |
elements Total time | Total time |
N Tf Tf / N | Tq Tq / N | Δ
-------------------------------------------------------------------------------------------
100 0.000012 sec 1.225 µs | 0.000004 sec 0.428 µs | -65.10 %
194 0.000016 sec 0.814 µs | 0.000009 sec 0.439 µs | -46.04 %
374 0.000026 sec 0.690 µs | 0.000023 sec 0.604 µs | -12.40 %
724 0.000043 sec 0.592 µs | 0.000058 sec 0.795 µs | +34.29 %
1398 0.000099 sec 0.707 µs | 0.000155 sec 1.112 µs | +57.28 %
2702 0.000204 sec 0.753 µs | 0.000300 sec 1.111 µs | +47.44 %
5220 0.000410 sec 0.786 µs | 0.000620 sec 1.187 µs | +51.02 %
10085 0.000845 sec 0.838 µs | 0.001254 sec 1.243 µs | +48.41 %
19483 0.002205 sec 1.132 µs | 0.002672 sec 1.372 µs | +21.21 %
37640 0.004242 sec 1.127 µs | 0.005436 sec 1.444 µs | +28.15 %
72716 0.006886 sec 0.947 µs | 0.011171 sec 1.536 µs | +62.23 %
140479 0.011156 sec 0.794 µs | 0.022899 sec 1.630 µs | +105.26%
271388 0.018773 sec 0.692 µs | 0.045749 sec 1.686 µs | +143.70%
524288 0.037429 sec 0.714 µs | 0.093858 sec 1.790 µs | +150.76%
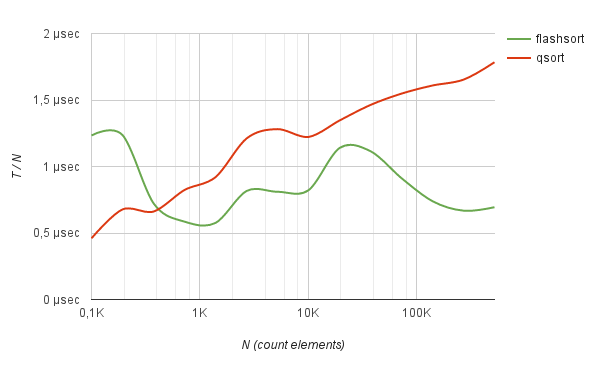
Аналогичные результаты выдает и сортировка случайных строк заданной длины. Например, список случайных хешей, кодированных в base64.
benchmark Sorting of hashes base64
---------------------------------------------------------------------------------------------
Count Flash-sort | Quick-sort |
elements Total time | Total time |
N Tf Tf / N | Tq Tq / N | Δ
---------------------------------------------------------------------------------------------
147 0.000009 sec 0.609 µs | 0.000010 sec 0.694 µs | +13.97 %
274 0.000025 sec 0.918 µs | 0.000027 sec 0.991 µs | +7.95 %
512 0.000053 sec 1.036 µs | 0.000061 sec 1.195 µs | +15.37 %
955 0.000098 sec 1.024 µs | 0.000135 sec 1.416 µs | +38.32 %
1782 0.000164 sec 0.921 µs | 0.000279 sec 1.566 µs | +70.04 %
3326 0.000315 sec 0.947 µs | 0.000581 sec 1.745 µs | +84.31 %
6208 0.000629 sec 1.013 µs | 0.001210 sec 1.949 µs | +92.39 %
11585 0.001325 sec 1.144 µs | 0.002378 sec 2.053 µs | +79.50 %
21618 0.002904 sec 1.343 µs | 0.004712 sec 2.180 µs | +62.26 %
40342 0.006132 sec 1.520 µs | 0.009752 sec 2.417 µs | +59.03 %
75281 0.010780 sec 1.432 µs | 0.019778 sec 2.627 µs | +83.47 %
140479 0.023484 sec 1.672 µs | 0.043534 sec 3.099 µs | +85.37 %
262144 0.044967 sec 1.715 µs | 0.082878 sec 3.162 µs | +84.31 %
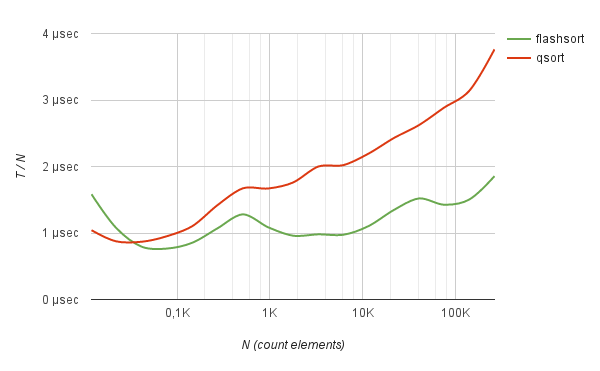
Однако метод работает без явного преимущества: лишь чуть шустрее, чем quick-sort во время сортировки случайно перемешанных английских слов.
benchmark Sorting of english words
---------------------------------------------------------------------------------------------
Count Flash-sort | Quick-sort |
elements Total time | Total time |
N Tf Tf / N | Tq Tq / N | Δ
---------------------------------------------------------------------------------------------
140 0.000016 sec 1.166 µs | 0.000014 sec 0.993 µs | -14.85 %
261 0.000030 sec 1.168 µs | 0.000029 sec 1.114 µs | -4.59 %
485 0.000055 sec 1.139 µs | 0.000061 sec 1.259 µs | +10.59 %
901 0.000141 sec 1.565 µs | 0.000158 sec 1.750 µs | +11.82 %
1673 0.000269 sec 1.608 µs | 0.000315 sec 1.884 µs | +17.17 %
3106 0.000536 sec 1.726 µs | 0.000655 sec 2.110 µs | +22.27 %
5766 0.001013 sec 1.756 µs | 0.001263 sec 2.191 µs | +24.76 %
10703 0.002007 sec 1.875 µs | 0.002525 sec 2.359 µs | +25.85 %
19868 0.004152 sec 2.090 µs | 0.005150 sec 2.592 µs | +24.04 %
36880 0.008459 sec 2.294 µs | 0.010266 sec 2.784 µs | +21.36 %
68458 0.017460 sec 2.550 µs | 0.021423 sec 3.129 µs | +22.70 %
127076 0.035615 sec 2.803 µs | 0.041683 sec 3.280 µs | +17.04 %
235885 0.075747 sec 3.211 µs | 0.086523 sec 3.668 µs | +14.23 %
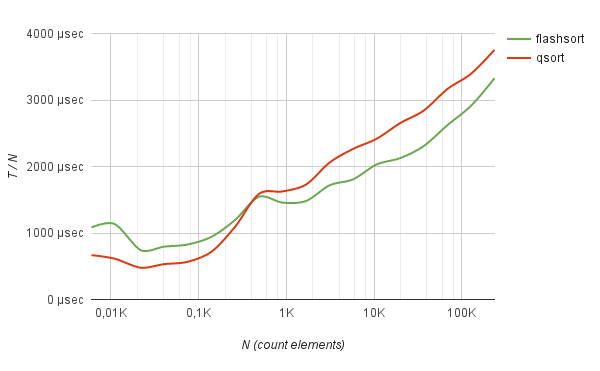
Неплохо метод показывает себя в работе с часто-повторяющимися данными. Например, сортировка логов полумиллиона IP-адресов (взятых из реальной жизни) методом flash-sort работает в 5 раз быстрее, чем быстрая сортировка.
benchmark Sorting of IP-addresses log
---------------------------------------------------------------------------------------------
Count Flash-sort | Quick-sort |
elements Total time | Total time |
N Tf Tf / N | Tq Tq / N | Δ
---------------------------------------------------------------------------------------------
107 0.000010 sec 0.953 µs | 0.000011 sec 1.056 µs | +10.78 %
208 0.000013 sec 0.639 µs | 0.000010 sec 0.480 µs | -25.00 %
407 0.000024 sec 0.584 µs | 0.000033 sec 0.812 µs | +39.01 %
793 0.000039 sec 0.493 µs | 0.000073 sec 0.915 µs | +85.61 %
1547 0.000080 sec 0.517 µs | 0.000211 sec 1.367 µs | +164.15%
3016 0.000169 sec 0.560 µs | 0.000512 sec 1.697 µs | +202.80%
5881 0.000308 sec 0.523 µs | 0.000962 sec 1.636 µs | +212.67%
11466 0.000548 sec 0.478 µs | 0.001812 sec 1.581 µs | +230.48%
22354 0.001034 sec 0.463 µs | 0.004191 sec 1.875 µs | +305.26%
43584 0.002109 sec 0.484 µs | 0.008693 sec 1.994 µs | +312.26%
84974 0.004411 sec 0.519 µs | 0.016003 sec 1.883 µs | +262.81%
165670 0.008837 sec 0.533 µs | 0.037358 sec 2.255 µs | +322.75%
323000 0.016046 sec 0.497 µs | 0.081251 sec 2.516 µs | +406.36%
629739 0.030895 sec 0.491 µs | 0.164283 sec 2.609 µs | +431.75%
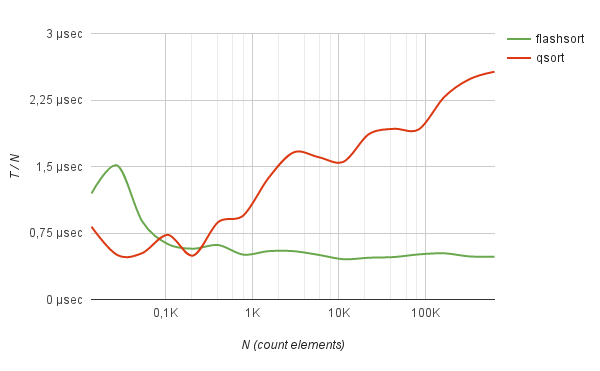
Причем на подобных данных время сортировки растет строго линейно от количества сортируемых элементов.
В заключение
Несмотря на то что представленный тут метод сортировки всегда делает строго O (N) перестановок, все же наивно было бы ожидать, что для всех типов данных во всех случаях алгоритм будет работать за линейное время. Вполне очевидно, что на практике скорость его работы будет зависеть и от характера сортируемых данных.
Выполнение алгоритма в общем случае будет происходить за нелинейное время хотя бы только потому, что на этапе перестановки элементов ему необходимо обращаться к случайным участкам памяти.
Однако полагаю, что все же еще есть простор для оптимизации описанного тут метода. Например, на первом этапе алгоритма, помимо подсчета количества элементов, попадающих в корзину, возможно вести еще какую-то более сложную статистику и уже на ее основании выбирать различные методы для сортировки элементов внутри корзины. Уверен, что в конечном счете хорошим решением могла бы стать разработка подобного гибридного алгоритма, объединяющего в себе подходы различных методов сортировки, а также оптимизацию под конкретное физическое представление данных в памяти или на диске.
Однако эти вопросы выходят за рамки статьи, целью которой было лишь показать возможности методов сортировки «не сравнением» в чистом их виде. В любом случае считаю, что в вопросах сортировки данных еще пока рано ставить точку.
