Физики & Пiв003.07.2021 17:32

Еще в 2013 году Хавьер Родригес-Родригес, физик из Мадридского университета Карлоса III, и несколько коллег представили экспериментальные данные и результаты компьютерного моделирования того, почему пiвные бутылки так сильно вспениваются после встряхивания. Они пришли к выводу, что вспенивание возникло в результате серии волн.

По всей видимости, физика похожа на развитие облака в атомной бомбе, хотя источник «взрыва» совсем другой.

Первоначальный удар создает ударную волну, которая распространяется от верха до дна бутылки. Энергия этой ударной волны передается пiву, посылая вторую ударную волну, отражающуюся взад и вперед между дном бутылки и поверхностью пiва. Вся эта «деятельность» высвобождает крошечные скопления газа, застрявшие в мелких дефектах стекла бутылки, создавая облака более мелких пузырьков из растворенного в пiве CO2 . По мере того, как они поднимаются на поверхность, эти пузыри становятся больше и ускоряются, в конечном итоге создавая поток пены, который делает разлив пiва такой популярной шуткой в ​​пабах.

Физик покоряет сердце девушки

В 2020 году Остмейер опубликовал научную статью (о ней речь пойдёт позже)
«Физика разлива пiва — верхняя и нижняя бутылка», сосредоточив внимание на том, почему нижняя пивная бутылка пенится, а верхняя — нет.

Теперь Остмайер (второй слева, в заднем ряду), вдохновленный поездкой в ​​Мюнхен, на Пiвной ОктоберФест, для демонстрации последних достижений пiвной науки, обратил свое внимание на насущный и животрепещущий вопрос о траекториях полета пiвной подкладки.

Окто́берфест (Октябрьские народные гуляния,  нем. Oktoberfest, среди мюнхенцев также известные под названием «Wiesn» (на баварском диалекте — «луг»)) — фольклорный фестиваль (нем. Volksfest), ежегодно проводимый в Мюнхене (Германия), самое большое народное гуляние в мире.

[2106.08238] Beer Mats make bad Frisbees (arxiv.org)
«Пiвные коврики — плохие фрисби»

Пiвные коврики (по крайней мере, круглые) — это в основном тонкие плоские диски заданного радиуса и массы. Фрисби также тонкий плоский диск и физика его полета хорошо известна.

Характерная изогнутая верхняя поверхность фрисби по существу имеет ту же форму (если смотреть сбоку), что и аэродинамический профиль. Бросьте его с силой, достаточной для преодоления силы тяжести, направленной вниз, и он создаст подъемную силу. Конечно, существует также сопротивление воздуха, или лобовое сопротивление, действующее на летающую тарелку. Сопротивление зависит от угла атаки. Если угол отрицательный, он толкает воздух вверх и заставляет фрисби опускаться, в то время как положительный угол толкает фрисби вверх. Чтобы свести к минимуму раскачивание, профессиональные игроки в фрисби знают, что нужно добавлять вращение при броске, закручивать, чтобы их фрисби оставались на одном и том же уровне во время полета.

Но у пiвных ковриков нет характерного аэродинамического профиля фрисби, и это влияет на их аэродинамику. Остмейер и др. начал с предположения о горизонтальном полете коврика, и оси вращения перпендикулярной направлению его движения. Бросьте коврик для пiва, как фрисби, и вращение сначала стабилизирует ось вращения, oднако сила тяжести вскоре заставит коврик наклониться, что изменит угол атаки. Подъёмная сила всё ещё останется, но она будет сосредоточена ближе к передней кромке, а не к центру масс коврика. Из-за этого, коврик начнет прецессировать, заставляя его переворачиваться на бок и перемещаться вертикально.

Модель исследователей предсказала, что это должно произойти примерно через 0.45 секунды полета. Кроме того, модель показала, что коврик может иметь либо обратное вращение (которое стабильно), либо верхнее вращение (которое нестабильно). Таким образом, у коврика с большой вероятностью, в конце его полёта, будет обратное вращение.

Конечно,  каждое хорошее теоретическое предсказание должно быть проверено экспериментально, и беспорядочное разбрасывание пiвных ковриков в местном пабе не было бы строгим с научной точки зрения.

Остмайер и его команда построили сложнейшую, выполненую на основе последних достижений науки и техники, пусковую установку для запуска пiвных ковриков в свободный, но котролируемый полёт, из двух беговых дорожек с приводом от электродвигателя.

Впервые в истории, пусковая установка позволила научным исследователям контролировать горизонтальную скорость и скорость вращения каждого запуска пiвных ковриков.

Эскпериментаторы поместили пусковую установку на стол, затем поместили пiвной коврик между беговыми дорожками и запустили коврики с разной скоростью, отметив, где они приземляются на пол.

Траектории полета записывались с помощью высокоскоростных камер (Optronis CR600×2), и команда использовала программу Tracker для извлечения координат пiвного коврика в любой точке его траектории.

Tracker это бесплатный инструмент для анализа и моделирования видео, созданный на основе Java-фреймворка с открытым исходным кодом Open Source Physics (OSP).

CR600×2 — камера высокого быстродействия с высочайшей светочувствительностью до 12 000 ISO / ASA. Быстрые движения регистрируются с выдержкой всего в одну микросекунду. Камера делает 500 кадров в секунду при разрешении (1280×1024 пикселей). Типичные приложения находятся в диапазоне от 50 до 10 000 кадров в секунду.

Результаты последующего, долгого и кропотливого анализа данных, показали очень хорошее согласие с теоретическими предсказаниями.

Экспериментальные данные по запуску пiвных ковриковСвершилось чудо — эксперимент сошёлся с теорией!

Теоретическая модель Остмейера&Co также может быть использована для предсказания траекторий полета других типов летающих объектов, в том числе и НЛО.
Например, их модель предсказывает, что компакт-диск перевернется через 0.8 секунды, в то время как более крупный и тяжелый диск перевернется через 16 секунд. У летающей игральной карты самая короткая траектория из всех, она переворачивается всего за 241 миллисекунду.

«Даже Великий Рик Смит-младший, мировой рекордсмен по дальности бросания игральных карт, не может избежать того, чтобы его карты летели по кривой и заканчивали свой полёт обратным вращением, за время менее, чем пол-секунды.

Против науки — не попрешь! », — пишут авторы в сноске.

Мы поднимаем свои бокалы за Остмейера и его коллег,  за их развлекательную и информативную работу, движимую исключительно научным любопытством, и приносящую неоценимую пользу народному хозяству.

Так выпьем же За физиков!  

Aвторы отметили в своих благодарностях

Наши искренние извинения всем, кого ударили ковриком из-под пiва, будь-то из-за неточного прицеливания, или из-за того, что мы подстрекаем других к проведению глупых экспериментов.

Шутки в сторону!

Перевод статьи от 10 февраля 2020 https://arxiv.org/pdf/2002.02896.pdf

«Физика р0злива пiва — нижняя и верхняя бутылка»

Иоганн Остмейер
Институт им. Гельмгольца, Рейнский университет им. Фридриха-Вильгельма, Бонн, Германия

Абстракт

«Разлив пiва» — это хорошо известная шутка, когда бутылка с газированной жидкостью ударяется о другую сверху, при этом обычно нижняя бутылка вспенивается, а верхняя — нет. Хотя физика, приводящая к процессу вспенивания в нижней бутылке была исследована и хорошо задокументирована, на сегодняшний день нет никаких объяснений почему верхняя бутылка практически не производит пены. В этой статье мы описываем причины совершенно разного поведения двух бутылок .

1. Введение

Недавно в работах [1, 2] было показано , почему бутылка с пересыщенной карбонизированной жидкостью вспенивается после ударa сверху другой бутылкой, обычно также содержащей перенасыщенную жидкость, т.е. газ в жидкости расширяется и образовавшаяся пена поднимается и растекается по емкости.
Физико-пiвное сообщество об этом знает и хорошо разбирается в этом явлении.
Во время физических симпозиумов, как правило, проводится розыгрыш, который называется «разлив пiва».

Симпо́зиум (лат. symposium от др.-греч. συμπόσιον — «пиршество») совещание, научная конференция по какому-либо научному вопросу (обычно с участием представителей разных стран).

Здесь жертва розыгрыша держит открытую пiвную бутылку, а шутник ударяет верхнюю часть пiвной бутылки о дно своей (открытой) пiвной бутылки. Пiво из нижней бутылки вспенивается, и пiвная пена из горлышка попадает на руки жертвы, вызывая всеобщий добродушный смех.
Физика, определяющая вспенивание пiва, подробно описана в работе [1], а в разделе 2 мы дадим краткое объяснение этому явлению, внимательно следуя вышеупомянутой статье.
В работах [1, 2] отсутствует объяснение того, почему шутник уходит со сцены относительно невредимым и сухим, продолжая держать открытую пiвную бутылку, которой били жертву, демонстрируя, что пена из неё почти не выходит. Этот результат также легко описывается методами изложенными в работе [1], и является предметом этой статьи.

2. Физика пенообразования

Наиболее важные этапы р0злива пiва следующие.
Первоначальный «шок» из-за «постукивания» вызывает колебания радиуса R уже существующих в жидкости мелких пузырьков. Эти колебания под действием ударного давления pS (t) описывются, в хорошем приближении, теорией Рэлея-Плессета

где, R0 ≈ 180 мкм — типичный размер начального радиуса пузырька,
ρ = 103 кг/м³, плотность воды,
p0 = 1065 Па, атмосферное давление,
σ = 0.0434 Н/м, поверхностное натяжение между CO2 и воды,
γ = 1.304, коэффициент теплоемкости CO2 и
µ = 10–3 кг/м/с, вязкость жидкости.

При достижении первого минимума радиального размера через tmin ≈ 0.15 мс, пузырьки в нижней бутылкe схлопываются [4] по модели Бреннена [5] примерно на N фрагментов, примерно равных по размеру, где

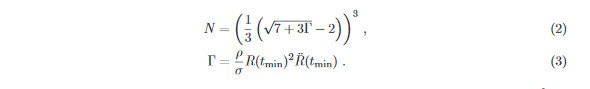
Kаждый начальный пузырь образует облако из N пузырьков меньшего размера, где обычно N ∼ 106. Таким образом, увеличенное количество пузырьков приводит к увеличению площади поверхности раздела между газом и жидкостью. Это приводит ко второй стадии, когда газ внутри жидкости диффундирует в пузырьки каждого облака. Объем облака, образованного пузырьками, растет во времени по закону квадратного корня √t [6] примерно в течение следующиx 10 мс.

И наконец, на последнем этапе, облако пузырьков становится настолько большим, что быстро поднимается вверх из-за своей плавучести. По мере продвижения онo собирает еще больше газа, что, в свою очередь, увеличивает размеры пузырей. Рост облака теперь масштабируется как t2, и облако принимает форму, напоминающую грибовидное облако от ядерного взрыва (см. светящиеся рисунки в [7]). Если образовались достаточно большие облака, то жидкость вспенивается примерно через 0.5 с после встряски.

Заинтересованный читатель может найти более подробное физическое объяснение процесса вспенивания, а также многие другие интересные явления, возникающие в газированных напитках, см. [7] .

3. Сравнение верхней и нижней бутылки

Последние два этапа не зависят ни от положения бутылки, ни от положения пузырька в ней.
Таким образом, достаточно исследовать схлопывание одиночного пузыря в фиксированном положении для того чтобы понять, почему верхняя бутылка (которую мы теперь обозначаем буквой U) не реагирует «столь яростно», как нижняя бутылка (теперь помечена L).
В самом деле, этa разница в поведении двуx бутылoк делает этот «фокус» таким привлекательным.

3.1 Начальное давление

Для начала, мы должны понять эволюцию ударной волны во времени.
Давление было вызвано встряской, и мы можем смоделировать затухающие колебания

где pA — начальная амплитуда, определяемая силой «удара»,
T = 0.24 мс [1], а t представляет время, прошедшее с момента первого достижения пузыря ударом.

Получается, что ударная волна теряет больше всего своей интенсивности из-за отражения от поверхности жидкости, а не во время движения в жидкости [1].
Таким образом, мы ожидаем время затухания будет порядка τ ≈ 2T, т.е. время, необходимое для достижения поверхности и отражения от неё. И мы можем видеть, что затухание не оказывает значительного влияния на качественное поведение вспенивания.

Разница между бутылками U и L заключается только в знаке pA,
где pA > 0 для верхней бутылки U, и pA < 0 для нижней L.
Это означает, что пузырьки в бутылке U сжимаются ударом и колеблются умеренно, тогда как пузырьки в бутылке L сначала расширяются, а затем резко схлопываются.
Это показано на рисунке 1, где мы построили временную эволюцию уравнения (1).

Решение этого обыкновенного дифференциального уравнения численно несложно, оно относится к классу Рунге-Кутта.
Измерения, выполненные в работах [1, 2], показывают хорошее согласие с численными прогнозами для различных начальных условий.

Рисунок 1: Радиус CO2-пузырька с момента первого возбуждения без затухания, τ = ∞. Полученный с помощью численного моделирования с использованием Рунге-Кутта. Черная (зеленая) кривая показывает поведение пузырьков в верхней (нижней) бутылке, которая имела положительноe (отрицательноe) начальноe давлениe от встряски

3.2 Схлопывание пузыря

Коллапс колеблющихся пузырьков описывается моделью Бреннена [5], согласно которой, самый нестабильный режим в основном отвечает за схлопывание пузырька в первом локальном минимуме до N ≈ nm3 фрагментов.

В то же время, коэффициент nm определяет фактор, по которому суммарная площадь всех дочерних пузырьков превосходит площадь поверхности исходного пузыря.
Поскольку эта площадь пропорциональна количеству поступающего CO2 пузырьков за счет диффузии, nm также является прямым индикатором интенсивности пенообразования.

Мы вычислили nm при различных начальных давлениях и демпфирующих силах.
Результаты этих вычислений показаны на рисунке 2.

Мы видим, что наиболее нестабильный режим растет в обеих бутылках с увеличением силы начального удара. Однако до тех пор, пока демпфирование не очень велико, nm растет очень быстро вызывая уменьшение pA в нижней бутылке L (−p0 < pA < 0).

В верхней бутылке U (0 < pA), nm растет медленно увеличивая pA .
В работе [1] nm ≈ 100.
Это означает, что в действительности затухание довольно мало и время затухания τ ≳ 2T.

Мы не можем определить затухание количественно, но и не обязаны.
Достаточно заметить, что для любого реалистичного сценария демпфированиe nm может быть на порядок больше в нижней бутылке L, чем в верхней бутылке U.

Единственным требованием для этого является такое сильное «постукивание», что pA ≈ −p0 .
Очевидно, что давление в верхней бутылке U не ограничено сверху, поэтому очень сильный удар может произвести pA ≫ p0 и вызвать вспенивание верхней бутылки.

Но, такая грубая сила встряски не представляет особого интереса и может привести к повреждению бутылок.

Рисунок 2: Наиболее нестабильный режим по модели Бреннена в зависимости от начального давления. Различные линии соответствуют разной силе демпфирования в уравнении (4). Черная линия была рассчитывается при отсутствии демпфирования.

4. Заключение

Хотя точная физика разлива пiва, включая гидродинамику, довольно сложна, однако легко понять, почему нижняя бутылка L пенится, а верхняя U (обычно) нет.

Встряска создает в бутылке L низкое давление, что приводит к расширению существующих пузырьков CO2, которые затем разбиваются на множество фрагментов.

Площадь поверхности CO2-жидкости растет, что в свою очередь заставляет больше газа диффундировать в кластер пузырьков. Он поднимается вверх и образует пену.

В верхней бутылкe U высокое начальное давление вызывает только умеренные колебания пузырьков, так что схлопывание не происходит, а если и происходит, то не так сильно.
Так или иначе, быстрый рост облака не происходит и шутник выигрывает пари.

Благодарности

Огромное спасибо Томасу Луу за множество полезных комментариев.

Я также хочу поблагодарить Катрин Гранталь, Карстена Урбаха и всех, с кем я когда-либо пил пiво за вдохновение и мотивацию в написании этой статьи.

Ссылки

[1] J. Rodrнguez-Rodrнguez, A. Casado-Chacуn and D. Fuster,
«Physics of Beer Tapping»,
Phys.Rev. Lett., vol. 113, p. 214 501, 21 2014.
doi: 10.1103/PhysRevLett.113.214501.

[2] V. Mantič-Lugo, A. Cayron, P.-T. Brun and F. Gallaire,
«Beer tapping: dynamics of bubbles after impact»,
Journal of Physics: Conference Series, vol. 656, p. 012029, 2015. [Online].
Available:  https://doi.org/10.1088%2F1742–6596%2F656%2F1%2F012029.

[3] M.P. Brenner, S. Hilgenfeldt and D. Lohse,
«Single-bubble sonoluminescence»,
Rev. Mod.Phys., vol. 74, pp. 425–484, 2 2002.
doi: 10.1103/RevModPhys.74.425.

[4] M.M. Daou, E. Igualada, H. Dutilleul, J.-M. Citerne, J. Rodrнguez-Rodrнguez, S. Zaleski and D. Fuster,
«Investigation of the collapse of bubbles after the impact of a piston on a liquid free surface»,
AIChE Journal, vol. 63, no. 6, pp. 2483–2495, 2017.
doi: 10.1002/aic.15725.

[5] C.E. Brennen, «Fission of collapsing cavitation bubbles»,
Journal of Fluid Mechanics, vol.472, 153–166, 2002.
doi: 10.1017/S0022112002002288.

[6] P.S. Epstein and M.S. Plesset,
«On the Stability of Gas Bubbles in Liquid-Gas Solutions»,
The Journal of Chemical Physics, vol. 18, no. 11, pp. 1505–1509, 1950.
doi: 10.1063/1.1747520.

[7] P. Vega-Martнnez, O.R. Enrнquez and J. Rodrнguez-Rodrнguez,
«Some Topics on the Physics of Bubble Dynamics in Beer»,
Beverages, vol. 3, no. 4, p. 38, 2017, issn: 2306–5710.
doi: 10.3390/beverages3030038.

++
Со своей стороны хочу заметить, что не смотря на «несерьёзность» и шутливый тон изложения, статья затрагивает глубокие физические проблемы гидродинамики.
Сам факт, что в статье приводятся ссылки на престижнейшие научные журналы такие как:

Phys.Rev. Lett.
Journal of Physics: Conference Series,
Rev. Mod.Phys.,
Journal of Fluid Mechanics,
The Journal of Chemical Physics,

говорит сам за себя.