Фальшивомонетчики против банкиров: стравливаем adversarial networks в Theano
Вы бы никогда не подумали, но это прогулка по пространству нейросети-фальшивомонетчика. Сделано крутейшими людьми Anders Boesen Lindbo Larsen и Søren Kaae Sønderby
Допустим, у нас есть задача — понять окружающий мир.
Давайте для простоты представим, что мир — это деньги.
Метафора, может быть, с некоторой моральной двусмысленностью, но в целом пример не хуже прочих — деньгам (банкнотам) определенно свойственна какая-то сложная структура, тут у них цифра, тут буква, а там хитрые водяные знаки. Предположим, нам нужно понять, как они сделаны, и узнать правило, по которым их печатают. Какой план?
Напрашивающийся шаг — это пойти в офис центрального банка и попросить их выдать спецификацию, но во-первых, вам ее не дадут, а во-вторых, если выдерживать метафору, то у вселенной нет центрального банка (хотя на этот счет есть религиозные разногласия).
Ну, раз так, давайте попробуем их подделать.
Вообще на тему понимания мира есть один достаточно известный подход, который заключается в том, что понять — значит распознать. То есть когда мы с вами занимаемся какой-то деятельностью в окружающем мире, мы учимся отличать одни объекты от других и использовать их потом соответственным образом. Вот это — стул, на нем сидят, а вот это — яблоко, и его едят. Путем последовательного наблюдения нужного количества стульев и яблок мы учимся отличать их друг от друга по указаниям учителя, и таким образом обнаруживаем в мире какую-то неоднородность и структуру.
Так работает довольно большое количество моделей, которые мы называем дискриминативными. Если вы немного ориентируетесь в машинном обучении, то в дискриминативную модель можно попасть, ткнув пальцем наугад куда угодно — многослойные перцептроны, решающие деревья и леса, SVM, you name it. Их задача — присваивать наблюдаемым данным правильную метку, и все они отвечают на вопрос «на что похоже то, что я вижу?»
Другой подход, слегка совершенно отличающийся, состоит в том, что понять — значит повторить. То есть если вы пронаблюдали за миром какое-то время, а потом оказались в состоянии реконструировать его часть (сложить бумажный самолетик, например), то вы кое-что поняли о том, как он устроен. Модели, которые так делают, обычно не нуждаются в указаниях учителя, и мы называем их порождающими — это всевозможные скрытые Марковские, наивные (и не наивные) Байесовские, а модный мир глубоких нейросетей с недавних пор добавил туда restricted Boltzmann machines и автоэнкодеры.
Фундаментальная разница в этих двух вещах вот в чем: для того, чтобы воссоздать вещь, ты должен знать о ней более-менее все, а для того, чтобы научиться отличать одну от другой — совершенно необязательно. Иллюстрируется лучше всего вот этой картинкой:
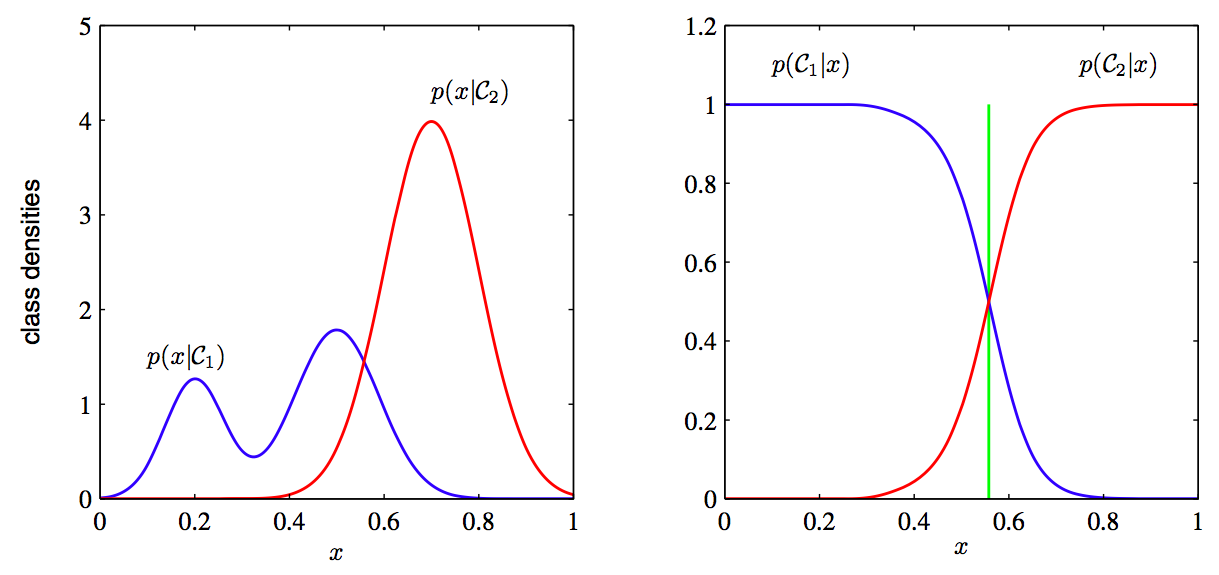
Слева — то, что видит порождающая модель (у синего распределения сложная бимодальная структура, а красное сильнее сужено), а справа — то, что видит дискриминативная (только граница, на которой проходит водораздел между двумя распределениями, и она понятия не имеет о прочей структуре). Дискриминативная модель видит мир хуже — она вполне может заключить, что яблоки отличаются от стульев только тем, что они красные, и для ее целей этого вполне хватит.
У обеих моделей есть свои преимущества и недостатки, но давайте пока для нашей цели согласимся, что порождающая модель просто круче. Нам нравится идея понимать вещи целиком, а не попарно-сравнительно.
Ну ладно, а как нам настроить эту порождающую модель? Для каких-то ограниченных случаев мы можем воспользоваться просто теорией вероятности и теоремой Байеса — скажем, мы пытаемся моделировать броски монетки, и предполагаем, что они соответствуют биномиальному распределению, тогда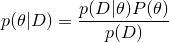 
и так далее. Для действительно интересных объектов вроде картинок или музыки это не очень работает — проклятье размерности дает о себе знать, признаков становится слишком много (и они зависят друг от друга, поэтому приходится строить совместное распределение…).
Более абстрактная (и интересная) альтернатива — предположить, что вещь, которую мы моделируем, можно представить в виде небольшого количества скрытых переменных или «факторов». Для нашего гипотетического случая денег это предположение выглядит вроде вполне интуитивно правильным — рисунок на купюре можно разложить на компоненты в виде номинала, серийного номера, красивой картинки, надписи. Тогда можно сказать, что наши исходные данные можно сжать до размера этих факторов и восстановив обратно, не потеряв смыслового содержимого. На этом принципе работают всевозможные автоэнкодеры, пытающиеся сжать данные и потом построить их максимально точную реконструкцию — очень интересная штука, про которую мы, правда, говорить не будем.
Еще один способ предложил Иэн Гудфеллоу из Google, и заключается он вот в чем:
1) Мы создаем две модели, одну — порождающую (назовем ее фальшивомонетчиком), и вторую — дискриминативную (эта пусть будет банкиром)
2) Фальшивомонетчик пытается построить на выходе подделку на настоящие деньги, а банкир — отличить подделку от оригинала (обе модели начинают с рандомных условий, и поначалу выдают в качестве результатов шум и мусор).
3) Цель фальшивомонетчика — сделать такой продукт, который банкир не мог бы отличить от настоящего. Цель банкира — максимально эффективно отличать подделки от оригиналов. Обе модели начинают игру друг против друга, где останется только один.
Обе модели будут нейронными сетями — отсюда название adversarial networks. Статья утверждает, что игра со временем сходится к победе фальшивомонетчика и, соотвественно, поражению банкира. Хорошие новости для преступного мира порождающих моделей.
Назовем нашего фальшивомонетчика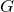 
(или generator), а банкира — 
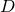(или discriminator). У нас есть какое-то количество оригинальных денег 
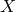для банкира, и пусть на выходе у него будет число диапазоном от нуля до единицы, чтобы оно выражало уверенность банкира в том, что выданные ему на рассмотрение деньги настоящие. Еще — поскольку фальшивомонетчик у нас нейронная сеть, ей нужны какие-то входные данные, назовем их 
. На самом деле это просто случайный шум, который модель будет стараться превратить в деньги.
Тогда, очевидно, цель фальшивомонетчика — это максимизировать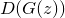 
, то есть сделать так, чтобы банкир был уверен, что подделки — настоящие.
Цель банкира посложнее — ему нужно одновременно положительно опознавать оригиналы, и отрицательно — подделки. Запишем это как максимизацию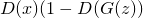 
. Умножение можно превратить в сложение, если взять логарифм, поэтому получаем:
Для банкира: максимизировать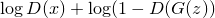 
Для фальшивомонетчика: максимизировать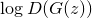 
Это чуть менее чем вся математика, которая нам здесь понадобится.
(почти целиком взят из этого замечательного поста, но там — на TensorFlow)
Давайте попробуем решить простой одномерный пример: пусть наши модели имеет дело с обычными числами, которые сгустились вокруг точки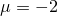 
с небольшим размахом 
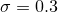. Вероятность каждого встреченного числа оказаться где-то на числовой прямой можно представить нормальным распределением. Вот таким:
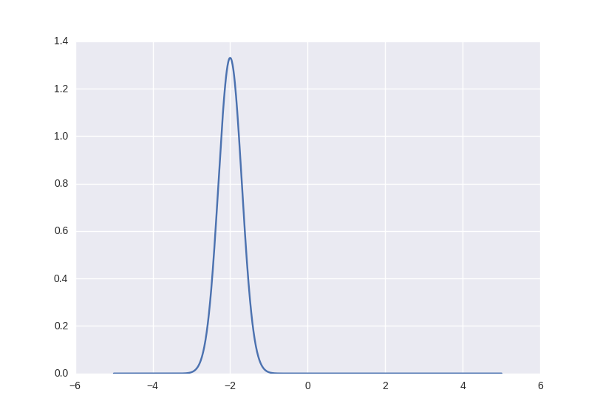
Соответственно числа, которые соответствуют этому распределению (живут в окрестности от -2) будут считаться «правильными» и «оригинальными», а остальные — нет.
Возьмем Theano и Lasagne, и зададим наши модели — простенькие нейронные сети с двумя слоями по десять нейронов каждый. При этом из-за механизма работы Theano (он строит символьный граф вычислений и позволяет в качестве входа дискриминатора задать одну конкретную переменную, а нам надо две — оригиналы и фальшивки) сделаем две копии дискриминатора: одна будет пропускать через себя «правильные» числа, а вторая — подделки генератора.
import theano
import theano.tensor as T
from lasagne.nonlinearities import rectify, sigmoid, linear, tanh
G_input = T.matrix('Gx')
G_l1 = lasagne.layers.InputLayer((None, 1), G_input)
G_l2 = lasagne.layers.DenseLayer(G_l1, 10, nonlinearity=rectify)
G_l3 = lasagne.layers.DenseLayer(G_l2, 10, nonlinearity=rectify)
G_l4 = lasagne.layers.DenseLayer(G_l3, 1, nonlinearity=linear)
G = G_l4
G_out = lasagne.layers.get_output(G)
# discriminators
D1_input = T.matrix('D1x')
D1_l1 = lasagne.layers.InputLayer((None, 1), D1_input)
D1_l2 = lasagne.layers.DenseLayer(D1_l1, 10, nonlinearity=tanh)
D1_l3 = lasagne.layers.DenseLayer(D1_l2, 10, nonlinearity=tanh)
D1_l4 = lasagne.layers.DenseLayer(D1_l3, 1, nonlinearity=sigmoid)
D1 = D1_l4
D2_l1 = lasagne.layers.InputLayer((None, 1), G_out)
D2_l2 = lasagne.layers.DenseLayer(D2_l1, 10, nonlinearity=tanh, W=D1_l2.W, b=D1_l2.b)
D2_l3 = lasagne.layers.DenseLayer(D2_l2, 10, nonlinearity=tanh, W=D1_l3.W, b=D1_l3.b)
D2_l4 = lasagne.layers.DenseLayer(D2_l3, 1, nonlinearity=sigmoid, W=D1_l4.W, b=D1_l4.b)
D2 = D2_l4
D1_out = lasagne.layers.get_output(D1)
D2_out = lasagne.layers.get_output(D2)
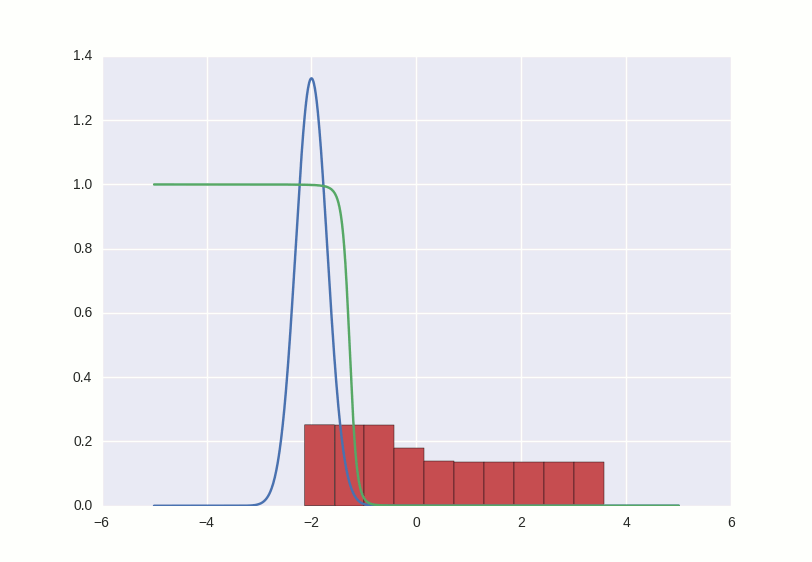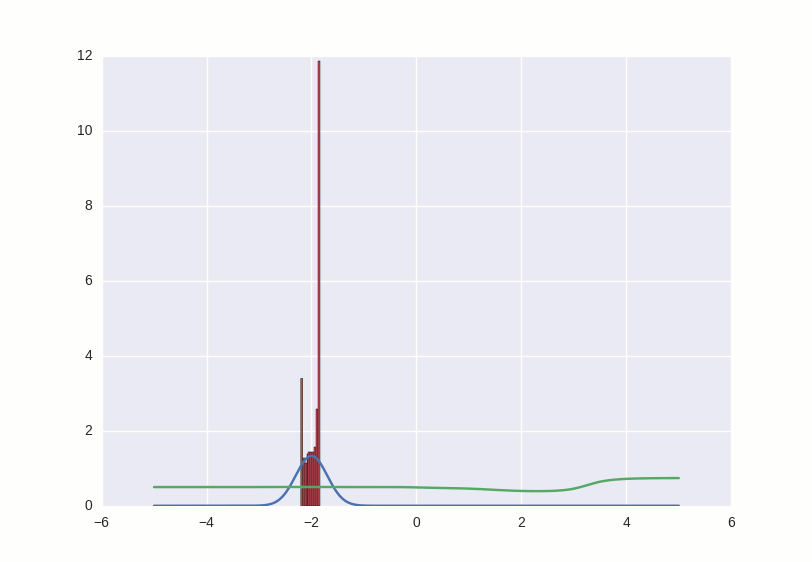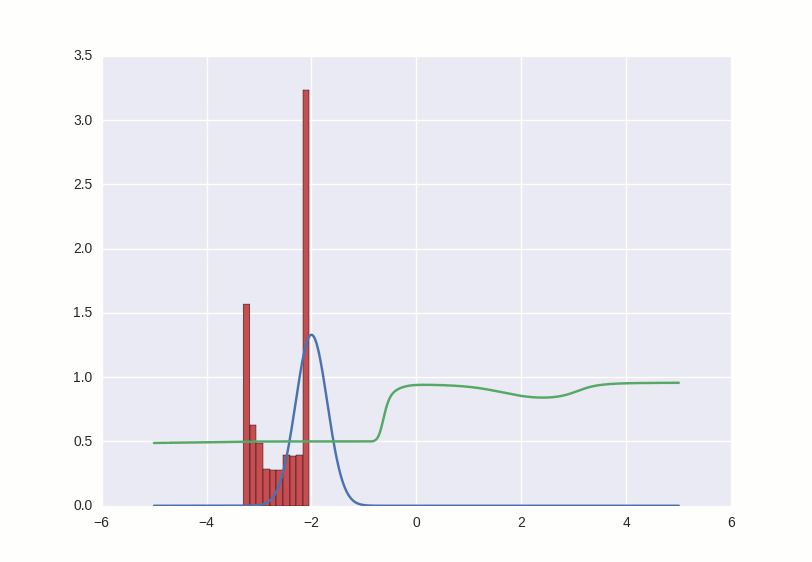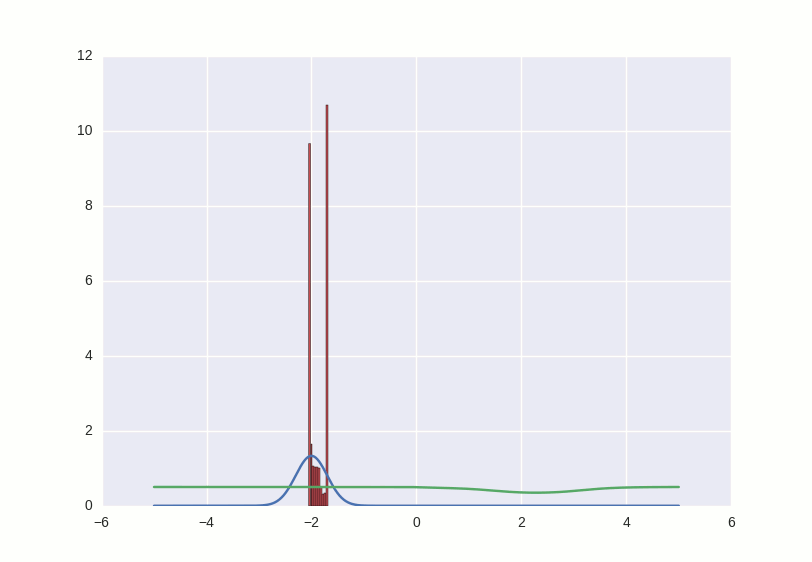
Давайте нарисуем, как ведет себя дискриминатор — то есть для каждого числа, которое есть на прямой (мы ограничимся диапазоном от -5 до 5) отметим уверенность дискриминатора в том, что это число — правильное. Получим зеленую кривую на графике ниже — как видите, поскольку дискриминатор у нас не обучен, выдает он полную околорандомную ересь. И заодно попросим генератор выплюнуть какое-то количество чисел и нарисуем их распределение с помощью красной гистограммы:
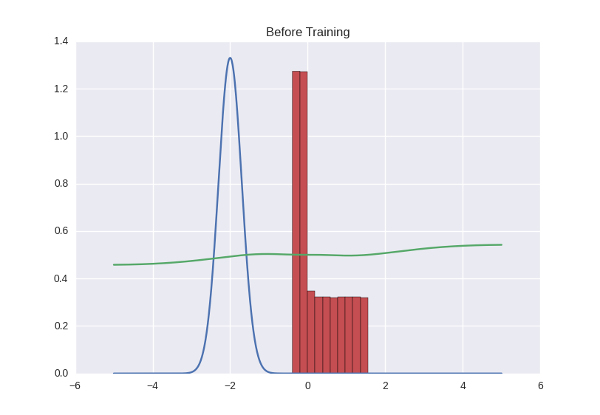
И еще немного Theano-кода, чтобы сделать функции цены и начать обучение:
# objectives
G_obj = (T.log(D2_out)).mean()
D_obj = (T.log(D1_out) + T.log(1 - D2_out)).mean()
# parameters update and training
G_params = lasagne.layers.get_all_params(G, trainable=True)
G_lr = theano.shared(np.array(0.01, dtype=theano.config.floatX))
G_updates = lasagne.updates.nesterov_momentum(1 - G_obj, G_params, learning_rate=G_lr, momentum=0.6)
G_train = theano.function([G_input], G_obj, updates=G_updates)
D_params = lasagne.layers.get_all_params(D1, trainable=True)
D_lr = theano.shared(np.array(0.1, dtype=theano.config.floatX))
D_updates = lasagne.updates.nesterov_momentum(1 - D_obj, D_params, learning_rate=D_lr, momentum=0.6)
D_train = theano.function([G_input, D1_input], D_obj, updates=D_updates)
# training loop
epochs = 400
k = 20
M = 200 # mini-batch size
for i in range(epochs):
for j in range(k):
x = np.float32(np.random.normal(mu, sigma, M)) # sampled orginal batch
z = sample_noise(M)
D_train(z.reshape(M, 1), x.reshape(M, 1))
z = sample_noise(M)
G_train(z.reshape(M, 1))
if i % 10 == 0: # lr decay
G_lr *= 0.999
D_lr *= 0.999
Используем здесь learning rate decay и не очень большой momentum. Кроме того, на один шаг генератора дискриминатор тренируется несколько шагов (20 в данном случае) — несколько мутный пункт, про который есть в статье, но не очень понятно, зачем. Мое предположение — это позволяет генератору не реагировать на случайные метания дискриминатора (т.е., фальшивомонетчик сначала ждет, пока банкир не утвердит для себя стратегию поведения, а потом пытается обмануть ее).
Процесс обучения выглядит примерно вот так:
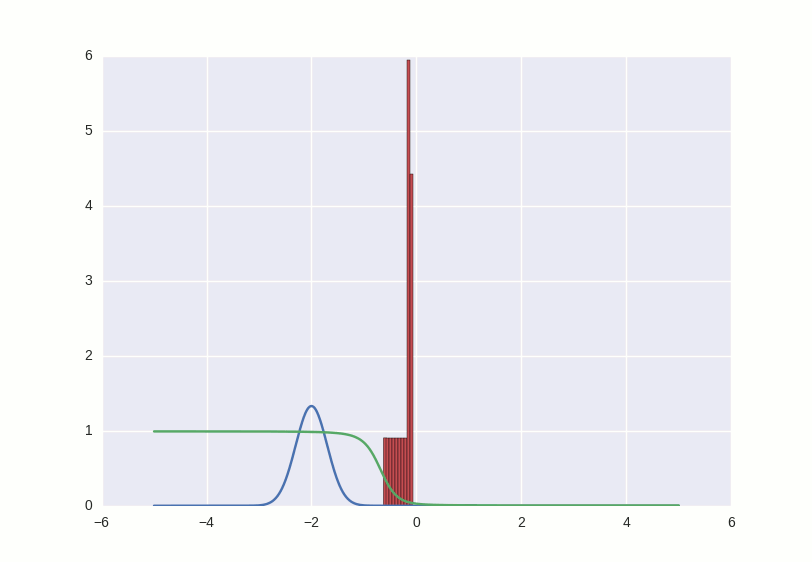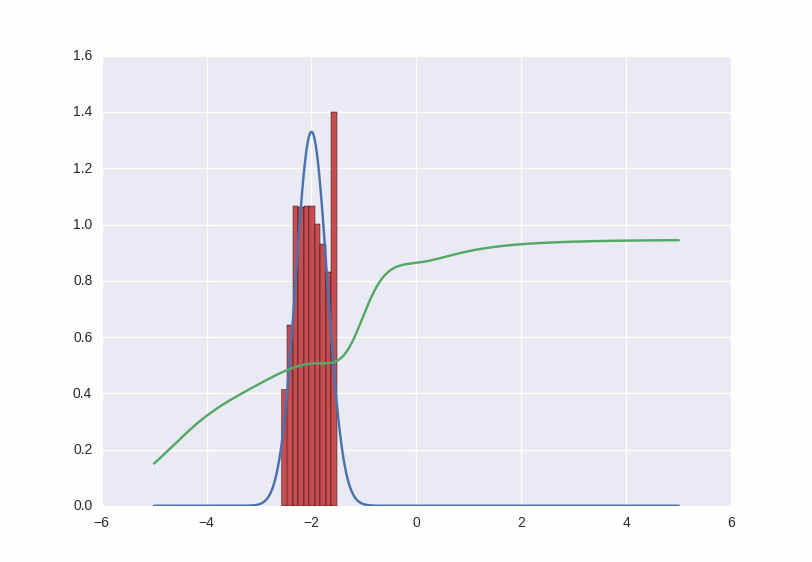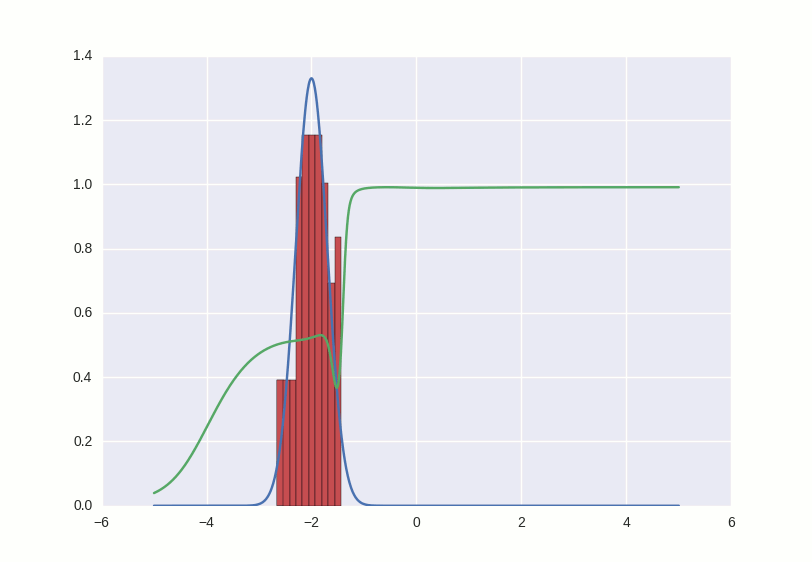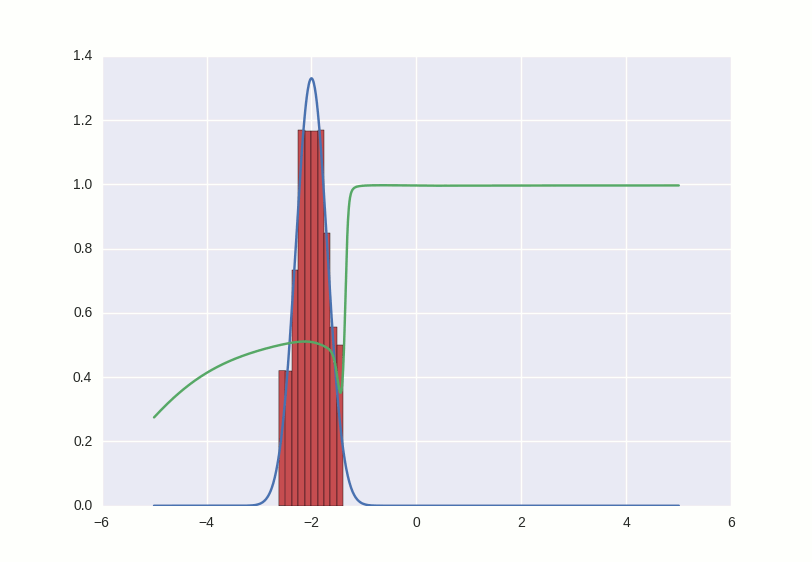
Что происходит в этой гифке? Зеленая линия старается загнать красную гистограмму в синий контур. Когда граница дискриминатора в определенном месте опускается ниже 0.5, это означает, что для соответствующих мест числовой прямой дискриминатор подозревает больше подделок, чем оригиналов, и скорее будет выдавать отрицательные заключения (тем самым он практически заталкивает выбросы красных чисел ниже — посмотрите, например, на выброс справа от центра распределения через первые несколько секунд гифки).
Там, где гистограмма совпадает с контуром, кривая дискриминатора держится на уровне 0.5 — это значит, что дискриминатор больше не может отличить подделки от оригиналов и делает лучшее, что может в такой ситуации — просто рандомно выплевывает догадки с одинаковой вероятностью.
За пределами интересующего нас участка дискриминатор ведет себя не очень адекватно — например, положительно с вероятностью ~1 классифицирует все числа большие -1 —, но это не страшно, потому что в этой игре мы болеем за фальшивомонетчика, и именно его успехи нас интересуют.
За этой парочкой любопытно наблюдать, играясь с разными параметрами. Например, если поставить momentum слишком большим, оба участника игры начнут слишком резко откликаться на обучающиеся сигналы и исправляют свое поведение так сильно, что делают еще хуже. Как-то так:
Целиком на код можно посмотреть здесь.
Ладно, это было не так уж плохо, но мы способны на большее, как намекает заглавная картинка. Попробуем новообретенные скиллы фальшивомонетчика на старых добрых рукописных цифрах.
Тут для генератора придется использовать небольшой трюк, который описан в статье под кодовым названием DCGAN (им же пользуются Ларс и Сорен в заглавном посте). Он состоит в том, что мы делаем такую своего рода сверточную сеть наоборот (разверточную сеть?), где заменяем subsampling-слои, уменьшающие картинку в N раз, на upsampling-слои, которые ее увеличивают, а сверточные слои делаем в режиме «full» — когда фильтр выскакивает за границы картинки и на выходе дает результат больше, чем исходная картинка. Если для вас это мутно и неочевидно, вот эта страница за пять минут все прояснит, а пока можно запомнить простое правило — в случае обычной свертки картинки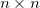 
фильтром 
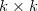результат будет иметь сторону 
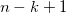, а full convolution — 
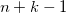. Это позволит нам начать с маленького квадратика шума и «развернуть» его в полноценное изображение.
Код генератора для цифр MNIST выглядит примерно как под спойлером. Дискриминатором будет какая-нибудь самая простая сверточная сеть. Если честно, я один-в-один содрал ее из readme к Lasagne, и даже не буду здесь приводить.
G_input = T.tensor4('Gx')
G = lasagne.layers.InputLayer((None, 1, NOISE_HEIGHT, NOISE_WIDTH), G_input)
G = batch_norm(lasagne.layers.DenseLayer(G, NOISE_HEIGHT * NOISE_WIDTH * 256, nonlinearity=rectify))
G = lasagne.layers.ReshapeLayer(G, ([0], 256, NOISE_HEIGHT, NOISE_WIDTH))
G = lasagne.layers.Upscale2DLayer(G, 2) # 4 * 2 = 8
G = batch_norm(lasagne.layers.Conv2DLayer(G, 128, (3, 3), nonlinearity=rectify, pad='full')) # 8 + 3 - 1 = 10
G = lasagne.layers.Upscale2DLayer(G, 2) # 10 * 2 = 20
G = batch_norm(lasagne.layers.Conv2DLayer(G, 64, (3, 3), nonlinearity=rectify, pad='full')) # 20 + 3 - 1 = 22
G = batch_norm(lasagne.layers.Conv2DLayer(G, 64, (3, 3), nonlinearity=rectify, pad='full')) # 22 + 3 - 1 = 24
G = batch_norm(lasagne.layers.Conv2DLayer(G, 32, (3, 3), nonlinearity=rectify, pad='full')) # 24 + 3 - 1 = 26
G = batch_norm(lasagne.layers.Conv2DLayer(G, 1, (3, 3), nonlinearity=sigmoid, pad='full')) # 26 + 3 - 1 = 28
G_out = lasagne.layers.get_output(G)
Результат оказывается примерно такой.
Не то чтобы идеально, но что-то определенно похожее. Забавно наблюдать, как генератор сначала учится рисовать похожими штрихами, а потом приличное время борется с тем, чтобы составить из них правильную форму. Например, вот здесь выделенные символы не похожи на цифры, но при этом явно представляют собой какие-то символы, то есть генератор пошел правильной дорогой:
Едем дальше — берем базу лиц LFW Crop, для начала уменьшаем лица до размера MNIST (28×28 пикселей) и пытаемся повторить эксперимент, только в цвете. И сразу замечаем несколько закономерностей:
1) Лица тренируются хуже. Количество нейронов и слоев, которое я тут приводил для MNIST, взято слегка с запасом — его можно уполовинить, и будет получаться неплохо. Лица при этом превращаются в непонятное рандомное месиво.
2) Цветные лица тренируются еще хуже — что объяснимо, конечно, информации становится в три раза больше.
3) Приходится иногда корректировать взаимное поведение генератора и дискриминатора: случаются ситуации, когда один загоняет другого в тупик, и игра останавливается. Обычно это происходит в ситуации, когда, скажем, дискриминатор оказывается мощнее в репрезентативном смысле — он может понимать такие тонкие детали, которые генератор еще (или вообще) не в состоянии различить. В опять-таки заглавном посте описано несколько эвристик (замедлять дискриминатор, когда он получает слишком хорошие оценки и т.д.), но у меня все достаточно неплохо работало и без них — хватало один раз в начале обучения подправить настройки и число нейронов.
И результат:
Неплохо-неплохо, но я все еще хочу что-нибудь такого же качества, как на КДПВ!
Я нагрузил опечаленную GT 650M полноразмерным (64×64) LFW Crop и оставил на ночь. К утру прошло примерно 30 эпох (на 10000 лиц), и конечный результат выглядел вот так:
Прелесть какая. Если кому нужны портреты персонажей для зомби-апокалипсиса, дайте знать! У меня их много.
Качество получилось не очень, но произошло что-то похожее на ту ситуацию с MNIST — наш генератор научился справляться с визуальными шумами и расплывчатостью, нормально рисовать глаза, носы и рты, и теперь у него проблема под названием «как их правильно совместить».
Давайте теперь подумаем еще раз, что у нас нарисовалось. Все эти лица выплевывает одна и та же сеть, а нейронная сеть — это насквозь детерминированная штука, просто последовательность умножений и сложений (и нелинейностей, ну ладно). Я не добавлял в генератор никакой рандомизации, dropout’а и т.д. Так каким образом лица получаются разные? Очевидно, единственный источник рандома, которым сеть может руководствоваться — это тот самый входной шум, который мы раньше обозвали «бессмысленным» параметром. Теперь выясняется, что он оказывается довольно важным — в этом шуме закодированы все параметры выходного лица, а все, что делает остальная сеть — это просто читает входной «рецепт» и в соответствии с ним наносит краску.
И рецепты не дискретны (я об этом не успел сказать, но в качестве шума бралось простое равномерное распределение чисел от 0 до 1). Правда, мы все еще не знаем, какое число в рецепте что именно кодирует, хм — и даже «кодирует ли что-нибудь осмысленное какое-то одно число?». Ну ладно, и зачем нам тогда это все?
Во-первых, зная теперь, что входной шум — это рецепт, мы можем им управлять. Равномерный шум, скажем прямо, был не очень хорошей идеей — теперь каждый кусочек шума может кодировать что угодно с одинаковой вероятностью. Мы можем подать на вход, скажем, нормальный шум (распределенный по Гауссу) — тогда значения шума, близкие к центру, будут встречаться часто и кодировать что-нибудь общее (типа цвета кожи), а редкие выбросы — что-нибудь особенное и редкое (например, очки на лице). Люди, писавшие статью про DCGAN, нашли несколько семантических кусков рецепта, и использовали их для того, чтобы надевать лицам очки или заставлять их хмуриться по желанию.
Во-вторых… видели мем на тему «image enhancing» из сериала CSI? Вещь над которой долго смеялись все люди, сколь-либо знакомые с компьютерами: могущественный алгоритм ФБР волшебным образом повышает разрешение картинки. Так вот, возможно, нам еще придется взять свои слова обратно, потому что, а почему бы нам немного не облегчить жизнь нашему генератору, и вместо того, чтобы подавать на вход шум, подать, скажем, уменьшенный вариант нашего оригинала? Тогда вместо того, чтобы рисовать лица из головы, генератору всего лишь надо будет их «дорисовать» —, а эта задача явно выглядит проще, чем первая.
У меня, к сожалению, не дошли до этого руки, но вот тут есть отличный пост, демонстрирующий, как это делается с впечатляющими иллюстрациями.
Ну и в-третьих, можно немного поразвлечься. Раз мы знаем, что рецепты не дискретны, то существуют переходные состояния между любыми двумя рецептами. Берем два вектора шума, интерполируем их и скармливаем генератору. Повторяем, пока не надоест, или пока люди в комнате серьезно не начнут беспокоиться, зачем вы так пристально разглядываете агонизирующих зомби.
1) Adversarial networks — это весело.
2) Если вы решите попробовать тренировать их сами — проще подсмотреть готовые рецепты, чем играться с параметрами.
3) Иошуа Бенджио назвал DCGAN и LAPGAN (это который image enhancing) в числе самых впечатляющих штук в машинном обучении 2015 года и именно после этого я полез про них читать, само собой
4) В еще одном блоге был на днях хороший пост на тему «deep learning is easy, try something harder» — как раз для людей вроде меня, которые зацепились за популярную тему и не очень понимают, куда двигаться дальше. Adversarial networks — хороший вариант (и тоже упоминается в посте как одно из новых перспективных направлений), потому что тут куча всего интересного, и контроль над рецептами только одна из самых напрашивающихся вещей.
5) Как перевести «adversarial networks» на русский язык? «Враждующие сети»? «Соперничающие сети»?
