Extremum Seeking Control в системе адаптивного круиз-контроля автомобиля

Введение
Существует множество подходов к управлению адаптивным круиз-контролем: ПИД-контроллеры, управление на основе нечёткой логики, MPC-контроллеры и др. MPC-контроллеры, из-за решения задачи оптимизации в пределах каждого шага расчета, довольно требовательны к целевой платформе. Остальные способы управления, несмотря на простоту настройки и физической реализации, не способны обеспечить оптимальное функционирование во всех режимах движения. Промежуточным решением этой проблемы является применение экстремального управления или управления на основе поиска экстремума (Extremum Seeking Control). В данной статье кратко коснемся того, что же такое управление на основе поиска экстремума, в чём его преимущества и недостатки, а также предложим общие рекомендации по настройке таких контроллеров. Тут вы не найдете исчерпывающих объяснений по всем тонкостям управления, материал представляет собой больше «быстрый взгляд» на возможный подход к управлению системой адаптивного круиз-контроля.
Принцип работы
Управление на основе поиска экстремума — это алгоритм управления, не требующий модели объекта управления (ОУ), который используется для поиска оптимального управления системой с неизвестной динамикой или системой, режимы работы которой с течением времени меняются.
В определении неспроста используется термин оптимальное управление. В ES-контроллере формирование управляющего сигнала происходит в процессе максимизации некоторой целевой функции, и оптимальное управление соответствует точке экстремума этой целевой функции (отсюда и название Extremum Seeking).
Для наглядности рассмотрим работу ES-контроллера на примере системы с одним заданным режимом работы — то есть попробуем решить задачу статической оптимизации.
Ниже представлена структурная схема такой системы управления.
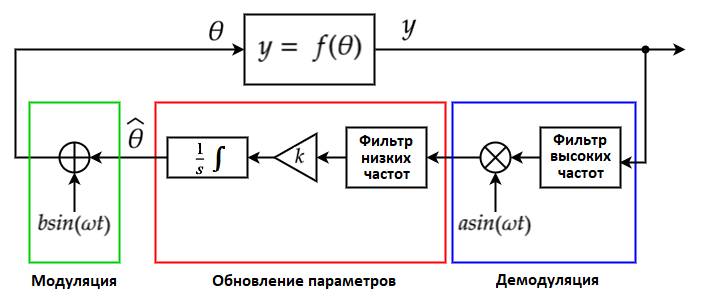
Рис. 1 — Структурная схема системы управления с ES-контроллером (статическая оптимизация)
Здесь y = f (θ) — объект управления, состоянием которого хотим управлять.
Пусть по параметрам объекта управления составлена некоторая целевая функция, максимальное значение которой соответствует оптимальному управлению (рисунок ниже). В общем случае целевая функция может принимать любой вид.
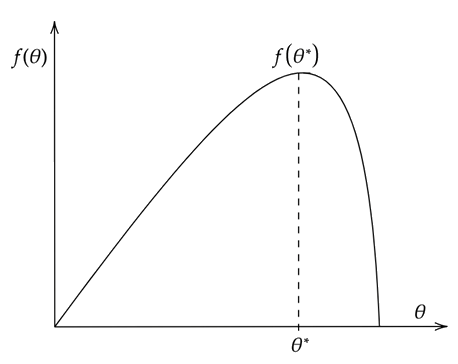
Рис. 2 — Пример графика целевой функции
Поиск оптимального управления начинается с некоторого начального приближения, задаваемого в интеграторе (рисунок 1).
Рассмотрим подробнее процесс формирования оптимального управления, который происходит в четыре этапа.
1. Модуляция — возмущение управляющего сигнала с помощью низкоамплитудного синусоидального сигнала заданной частоты.
Допустим, начальное приближение управляющего сигнала меньше оптимального, рисунок 3.
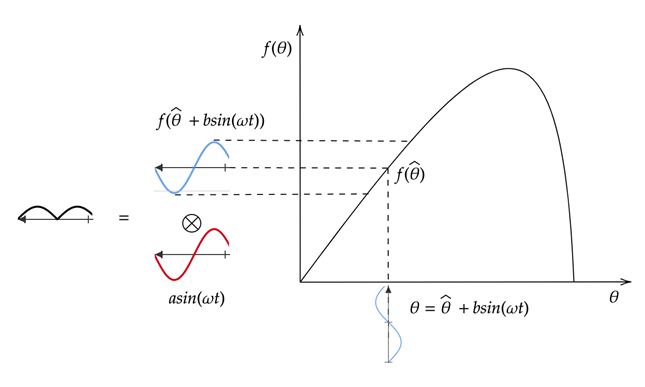
Рис. 3 — Оценка изменения целевой функции
(начальное приближение управляющего сигнала меньше оптимального)
На этапе модуляции к исходному управляющему сигналу прибавляется низкоамплитудный синусоидальный сигнал заданной частоты (частота модуляции). Это делается для того, чтобы в последствии оценить изменение целевой функции.
2. Отклик системы — реакция объекта управления на возмущенный (модулированный) управляющий сигнал.
Возмущенный сигнал управления изменяется по гармоническому закону. По графику на рисунке 3 видно, что с уменьшением управляющего сигнала (ветвь красного синусоидального графика идет вниз) значение целевой функции также уменьшается (ветвь голубого синусоидального сигнала также идет вниз), то есть при небольшом уменьшении начального приближения θ (по оси абсцисс) будем наблюдать уменьшение значения целевой функции f (θ) (по оси ординат). Аналогично имеем противоположную картину в случае увеличения управления.
3. Демодуляция — перемножение полученного значения целевой функции на синусоидальный сигнал с частотой, равной частоте модуляции.
Если перемножить синусоидальный сигнал с частотой, равной частоте модуляции, и полученное значение целевой функции (красный и голубой графики на рисунке 3), то получим график (синусоидальный сигнал черного цвета), результирующей функции, принимающей неотрицательные значения. Как правило, перед перемножением значение целевой функции дополнительно пропускают через фильтр высоких частот, поскольку нам важно отследить именно изменение целевой функции. Подробнее об этом можно почитать здесь.
Таким образом, на выходе демодуляции имеем некоторое положительное число, которое далее послужит для обновления начального приближения.
4. Обновление параметров — обновление текущего управляющего сигнала путем интегрирования демодулированного сигнала.
На заключительном этапе к текущему управляющему сигналу с некоторым усилением прибавляется величина демодулированного сигнала. Как правило, для удаления высокочастотного шума из демодулированного сигнала, также добавляют фильтр низких частот (рисунок 1).
В нашем примере демодулированный сигнал представляет собой некоторое положительное число. То есть обновленное значение управляющего сигнала станет больше, и на графике функции потерь (рисунок 2) обновленное управление сместится вправо в сторону оптимального θ*.
Таким образом, повторяя этапы 1–4, ES-контроллер будет приближать управление к оптимальному для заданного режима работы системы. Когда управление станет близким к оптимальному, величина демодулированного сигнала будет примерно равна нулю, и управляющий сигнал будет лишь незначительно колебаться в районе оптимального — рисунок 4.

Рис. 4 — Оценка изменения целевой функции (управляющий сигнал меньше оптимального)
Изначально мы приняли, что начальное приближение управления меньше оптимального. Давайте посмотрим, что будет в случае, когда на графике целевой функции (рисунок 2) начальное приближение правее экстремума, рисунок 5.
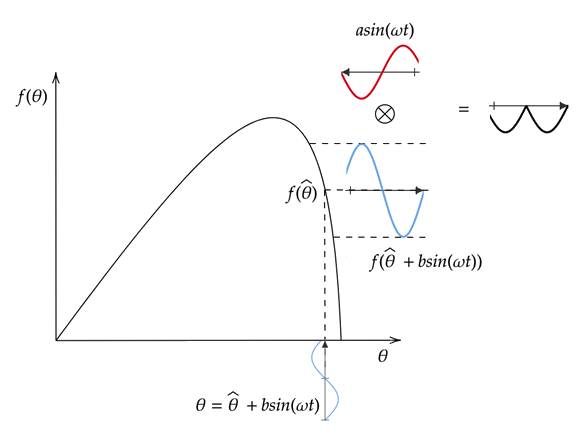
Рис. 5 — Оценка изменения целевой функции
(начальное приближение управляющего сигнала больше оптимального)
С уменьшением управляющего сигнала (ветвь красного синусоидального графика идет вниз) значение целевой функции теперь увеличивается (ветвь голубого синусоидального сигнала идет вверх). Аналогично имеем противоположную картину в случае увеличения управления.
Таким образом, в результате демодуляции мы теперь получим некоторое отрицательное число. И обновленное значение управляющего сигнала станет меньше начального приближения, и на графике функции потерь (рисунок 2) обновленное управление сместится влево в сторону оптимального θ*. По итогу ES-контроллер аналогично будет приближать управление к оптимальному.
При управлении системой, режимы работы которой с течением времени меняются, параметры целевой функции также могут меняться (рисунок 6). Здесь z = h (x) — вектор состояний объекта управления, a y = g (x) — изменяющаяся целевая функция, которую для поиска оптимального управления необходимо максимизировать.
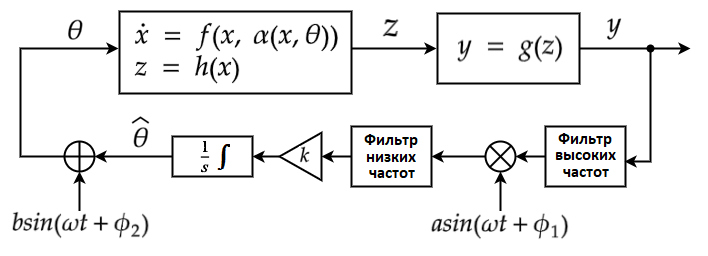
Рис. 6 — Структурная схема системы управления с ES-контроллером (динамическая оптимизация)
В этом случае будет решаться уже задача динамической оптимизации, то есть система управления будет пытаться находить экстремум постоянно обновляемой целевой функции f (θ**) — рисунок 7. В остальном алгоритм работы аналогичен рассмотренным шагам 1–4.
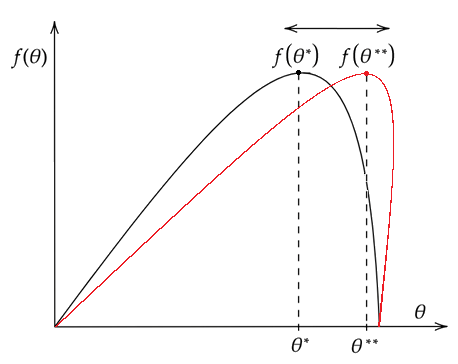
Рис. 7 — Изменение формы целевой функции при смене режимов работы системы
Можно заметить, что ES-контроллер имеет большое количество настраиваемых параметров:
Начальное приближение оптимизируемых параметров управления
Частота возмущающего (модулирующего) сигнала
Амплитуда модулирующего сигнала
Амплитуда демодулирующего сигнала
Частота среза фильтра высоких частот
Частота среза фильтра низких частот
Шаг спуска в задаче оптимизации (параметр k на рисунке 1).
Чуть позже на примере системы адаптивного круиз-контроля приведем общие рекомендации по настройке этих параметров. А пока подведем итог и выделим основные плюсы и минусы управления на основе поиска экстремума.
Плюсы:
Не требует модели объекта управления.
Адаптируется под разные рабочие режимы.
Целевая функция любого вида.
Минусы:
Большое количество настраиваемых параметров.
Не подходит для объектов управления, режимы работы которого меняются быстро (в этом случае поиск оптимального управления не будет успевать сходиться к оптимуму).
Не подходит для объектов управления, которые медленно реагируют на управляющий сигнал (нужно успевать оценивать изменение целевой функции).
Решается задача локальной, а не глобальной оптимизации.
Система адаптивного круиз-контроля
Принцип работы адаптивного круиз-контроля следующий: водитель устанавливает требуемую скорость автомобиля. И если дистанция до впереди идущего автомобиля больше безопасной, то автомобиль стремится набрать и удерживать эту скорость. Как только дистанция становится меньше минимально допустимой, автомобиль переходит в режим следования. Для режима следования водитель также может установить требуемую дистанцию до автомобиля спереди. Таким образом, пока дистанция до впереди идущего автомобиля будет больше безопасной, целью системы управления будет поддержание заданной скорости, в противном случае — поддержание безопасной дистанции (рисунок 8).
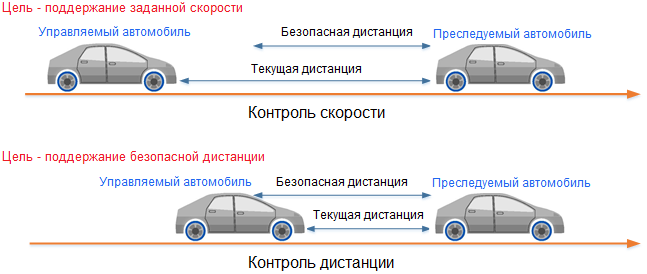
Рис. 8 — Принцип работы адаптивного круиз-контроля
Моделирование системы управления адаптивным круиз-контролем
Теперь соберем в Simulink нашу систему управления. Для упрощения, будем учитывать только кинематику движения автомобилей с некоторой инерционностью разгона/торможения, рисунок 9.
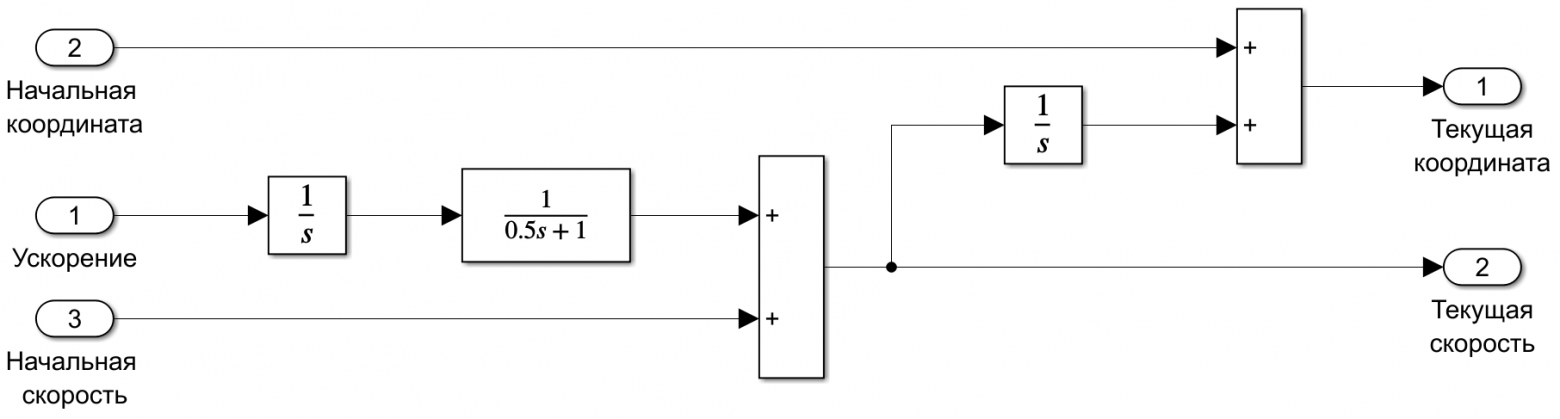
Рис. 9 — Упрощённая модель прямолинейного движения автомобиля
Заданная скорость движения или безопасная дистанция до впереди идущего автомобиля поддерживается пропорциональным контроллером с коэффициентами для ошибки по скорости, дистанции до автомобиля спереди и относительной скорости автомобилей K_v, K_x и K_vrel соответственно, рисунок 10.
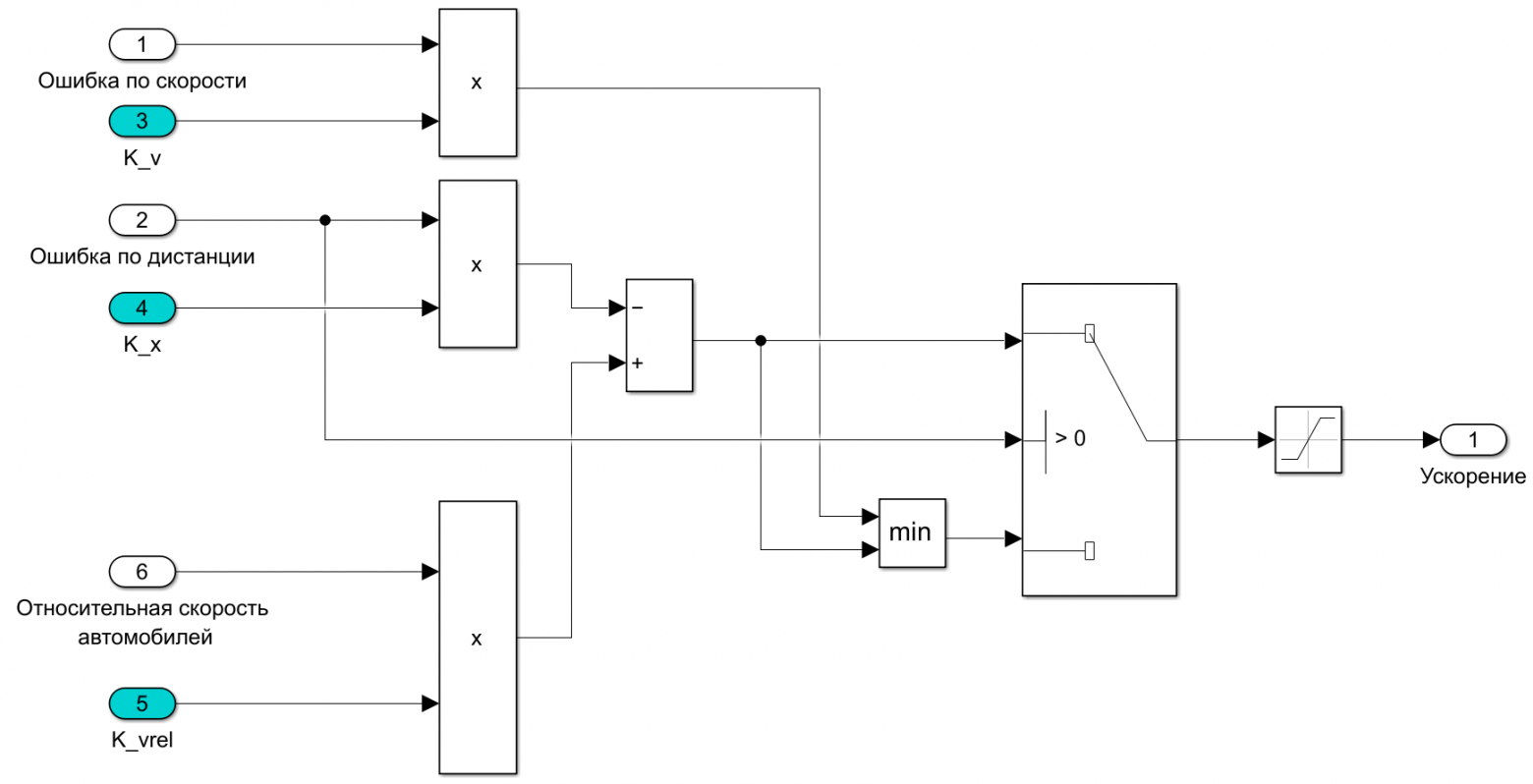
Рис. 10 — Модель пропорционального контроллера
В данном примере управление на основе поиска экстремума будет пытаться оптимизировать эти три коэффициента в процессе работы адаптивного круиз-контроля. Введем целевую функцию, учитывающую ошибки по относительной дистанции между автомобилями и скорости управляемого автомобиля. Также учтем изменение ускорения управляемого автомобиля, рисунок 11.
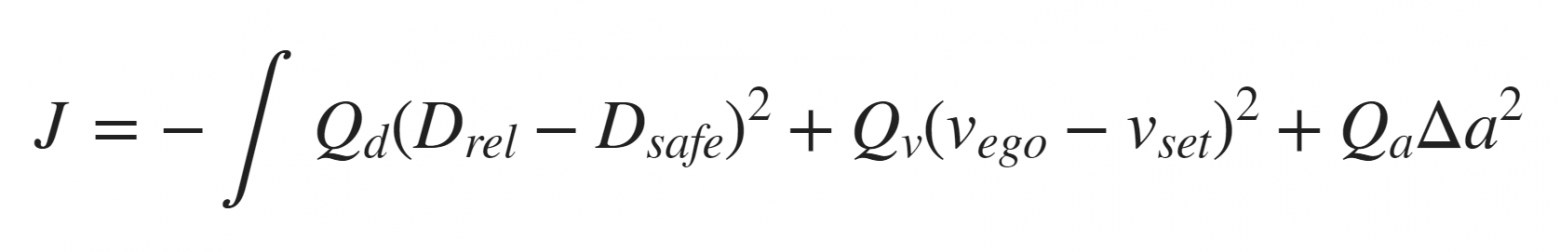
Рис. 11 — Пример целевой функции для системы адаптивного круиз-контроля
Структурная схема контура по поиску оптимального управления уже знакома и приведена ниже.

Рис. 12 — Структурная схема контура по поиску оптимального управления
Ниже приведены общие рекомендации по настройке параметров управления на основе поиска экстремума.
Начальное приближение оптимизируемых параметров управления:
Существенно влияет на качество управления, должно отдельно подбираться для основного рабочего режима системы.Частота возмущающего (модулирующего) сигнала:
Должна быть меньше основных рабочих частот системы, но при этом больше частот среза фильтров высоких и низких частот.Амплитуда демодулирующего сигнала:
Должна быть существенно больше амплитуды модулирующего сигнала (чем больше амплитуда демодулирующего сигнала, тем быстрее изменяются оптимизируемые параметры).Амплитуда модулирующего сигнала:
Должна быть существенно меньше амплитуды демодулирующего сигнала.Частота среза фильтра высоких частот:
Должна удовлетворять неравенству: ωh < ω/2π, где ω — частота возмущающего сигнала.Частота среза фильтра низких частот:
Должна удовлетворять неравенству: ωl > ω/2π.Шаг спуска в задаче оптимизации (параметр k на рисунке 12):
Влияет на скорость сходимости оптимизации (слишком большой шаг спускаможет привести к потере устойчивости системы — решение не будет сходиться к оптимальному).
Проверим работу системы управления на основе поиска экстремума в следующем тестовом сценарии: пусть управляемый автомобиль стартует за 400 м до автомобиля спереди с начальной скоростью 90 км/ч. Скорость автомобиля спереди изменяется по гармоническому закону в районе 20 км/ч. Заданная по круиз-контролю скорость управляемого автомобиля — 108 км/ч.
Результаты моделирования приведены на графиках ниже.
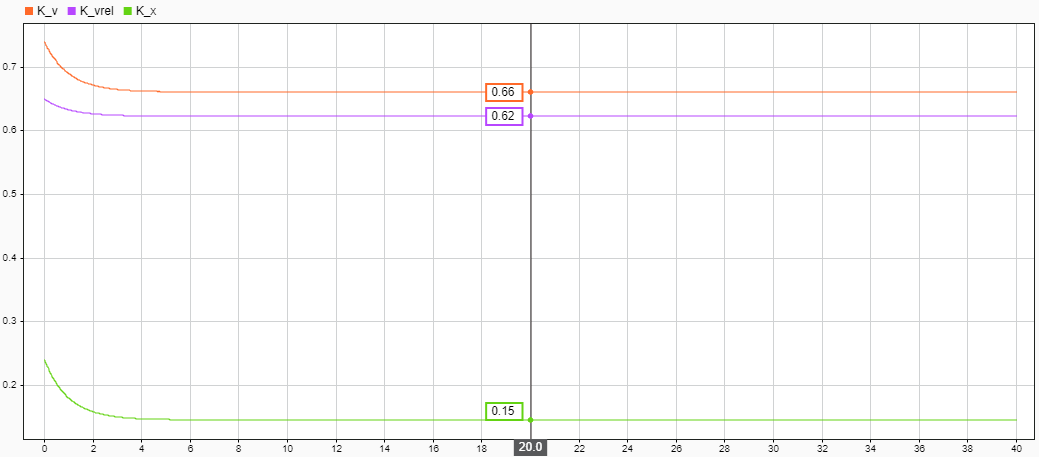
Рис. 13 — Результаты моделирования (оптимизируемые коэффициенты)
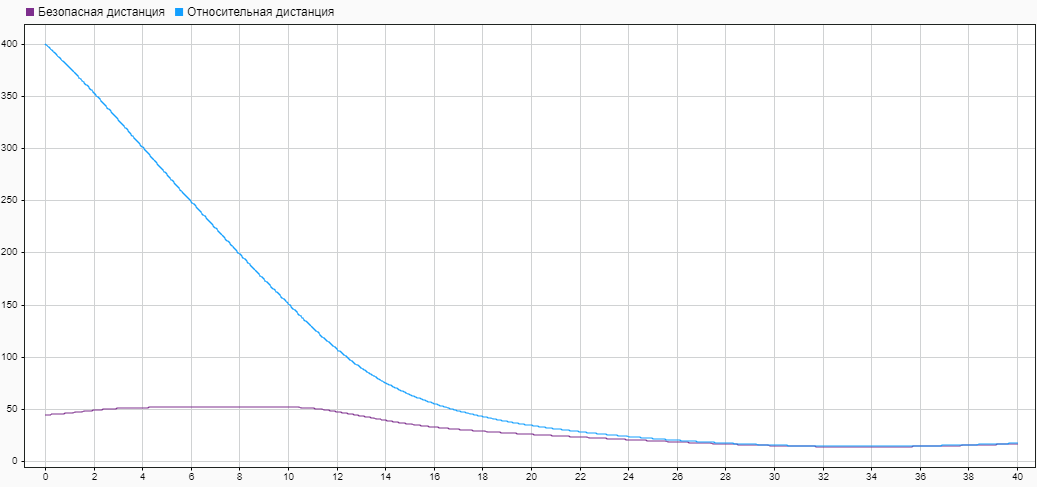
Рис. 14 — Результаты моделирования (поддержание безопасной дистанции)
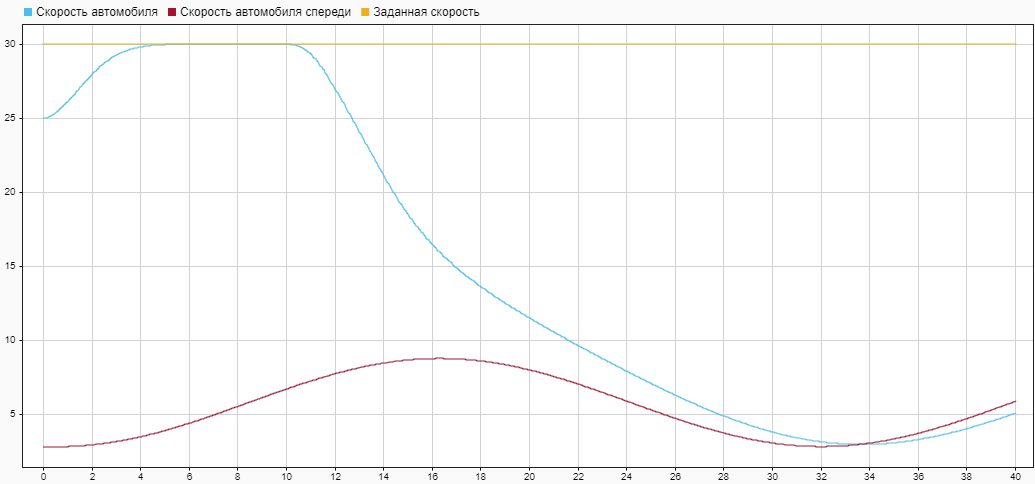
Рис. 15 — Результаты моделирования (скорость управляемого автомобиля)

Рис. 16 — Результаты моделирования (ускорение управляемого автомобиля)
По графикам видно, что коэффициенты пропорционального регулятора почти сразу из начального приближения пришли к некоторым оптимальным значениям. Относительная дистанция между автомобилями была в пределах безопасной. При этом в начальный момент времени, когда дистанция до автомобиля спереди была еще достаточно большой, управляемый автомобиль набрал требуемую по круиз-контролю скорость в 108 км/ч. Затем, по мере приближения к преследуемому автомобилю, система перешла в режим поддержания безопасной дистанции.
Заключение
Таким образом, несмотря на большое количество настраиваемых параметров, экстремальное управление может хорошо себя зарекомендовать в системе адаптивного круиз-контроля автомобиля. Наряду с точным поддержанием заданной скорости или безопасной дистанции профиль ускорения управляемого автомобиля выходит достаточно плавным.
Если Вам интересно всё, что связано с виртуальным тестированием систем помощи водителю, приходите на наш семинар, призванный собрать на одной площадке всех специалистов данной тематики для обмена знаний и опыта, чтобы вооружившись последними технологиями дать толчок в развитии безопасности дорожного движения.
