Эти ваши синусы
Откуда есть пошло земли измерение
Об этом, в общих чертах, знают все. Две с половиной тысячи лет назад, долина Нила, который постоянно то разливается, то убывает. Разливается и убывает, впрочем, не как ему вздумается, а более-менее регулярно. И даже более того: с течением времени люди понимают, что разливы, кажется, синхронизированы с появлением Сириуса на небе.
Вот, кстати, и он

Сейчас-то звёзды в городах особо не видны, а в то время залипать на Млечный путь наверняка было одним из главных развлечений. Сириус — самый яркий тут.
Житуха, сами понимаете, была тогда суровая и вопрос составления календарей, заглянув в которые можно было понять, когда нам сеять, когда жать, а когда пиво пить (его, к слову, тоже придумали то ли египтяне, то ли шумеры) был не праздным, а, можно сказать, экзистенциальным. А раз календари основаны на движении звёзд, то неплохо было бы поделить небесный свод на какие-то участки. В чём преуспели ещё в древнем Вавилоне, где жили хардкором и угорали по шестидесятеричной системе счисления.
Но небо-то там, высоко, а Нил гоняет свои воды туда-сюда тут, на земле. И участки земли приходилось делить заново всякий раз, когда, нанеся всякого плодородного река уходила. Как всем известно, тут-то и появилась геометрия, когда греки, насмотревшись на египетские треугольники (которые, собственно, они и назвали египетскими) начали у себя в Элладе вино попивать да углы измерять.
Многое, конечно, было наработано и до них, только являлось скорее практическим знанием, без какой-то строгой формализации даже на уровне античности. Так, например, был придуман гномон (более известный читателям, наверное, под названием «солнечные часы»)
Гномон и кион

Гномон слева

Хотя первые были просто палками на горизонтальной поверхности и выглядели скорее так
Что для своего времени было просто-таки хайтеком. Ясно, например, что длина тени будет меняться в течении дня и самой короткой окажется в полдень, а самой длинной — на восходе и на закате. А раз так, то во-первых можно зафиксировать путь, который проходит тень, и поделить его, скажем, на двенадцать частей, а каждую из частей назвать, ну, предположим, часом. Во-вторых в разное время года тень описывает разные пути и, если очень долго на них смотреть и немного пораскинуть мозгами, то можно вычислять солнцестояния, длину года и бог весть что ещё. В-третьих если мы знаем длину гномона и знаем длину тени, то мы можем… погодите-ка… поделить одно на другое и найти тангенс угловой высоты Солнца над горизонтом! Жаль, что тангенсы мы ещё не придумали, но возможности, согласитесь, поражают.
И тангенсы не придумают ещё достаточно продолжительное время. Будет Гиппарх и другие греческие учёные, которые, насколько мы понимаем по упоминаниям в других трудах (их собственные, к сожалению, не сохранились) крутили тригонометрический круг туда-сюда, вместо углов использовали хорды, синусом называли не отношение сторон, а сами стороны, а ещё придумали странноватые на наш вкус понятия наибольшего и полного синуса.
Ко всяким интересным выводам, впрочем, они прийти смогли. Например, их мысль вывела тот факт, что если возвести в квадрат хорду центрального угла, прибавить к ней тоже возведённую в квадрат хорду 180 градусов минус мера центрального угла, то мы получим диаметр в квадрате.
Как-то так
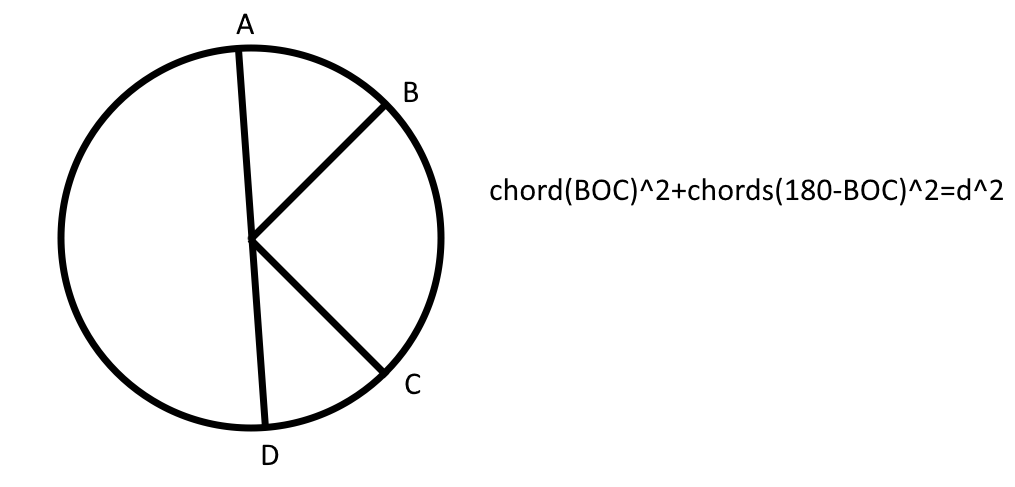
А ведь если сделать ещё один шаг (не самый очевидный, впрочем, по тем временам) и положить диаметр окружности равным единице, то получим практически основное тригонометрическое тождество! Без этих ваших косинусов, между прочим.
Но самым, наверное, тригонометричным греком будет Птолемей — большой любитель посмотреть на звёзды, чертежи построить да книжки пописать. Причём его magnum opus, «Альмагест», сохранится только в арабском переводе, который потом и попадёт обратно в Европу. В «Альмагесте», кстати говоря, и появляется что-то удивительно похожее на таблицу синусов.
Примерно такая
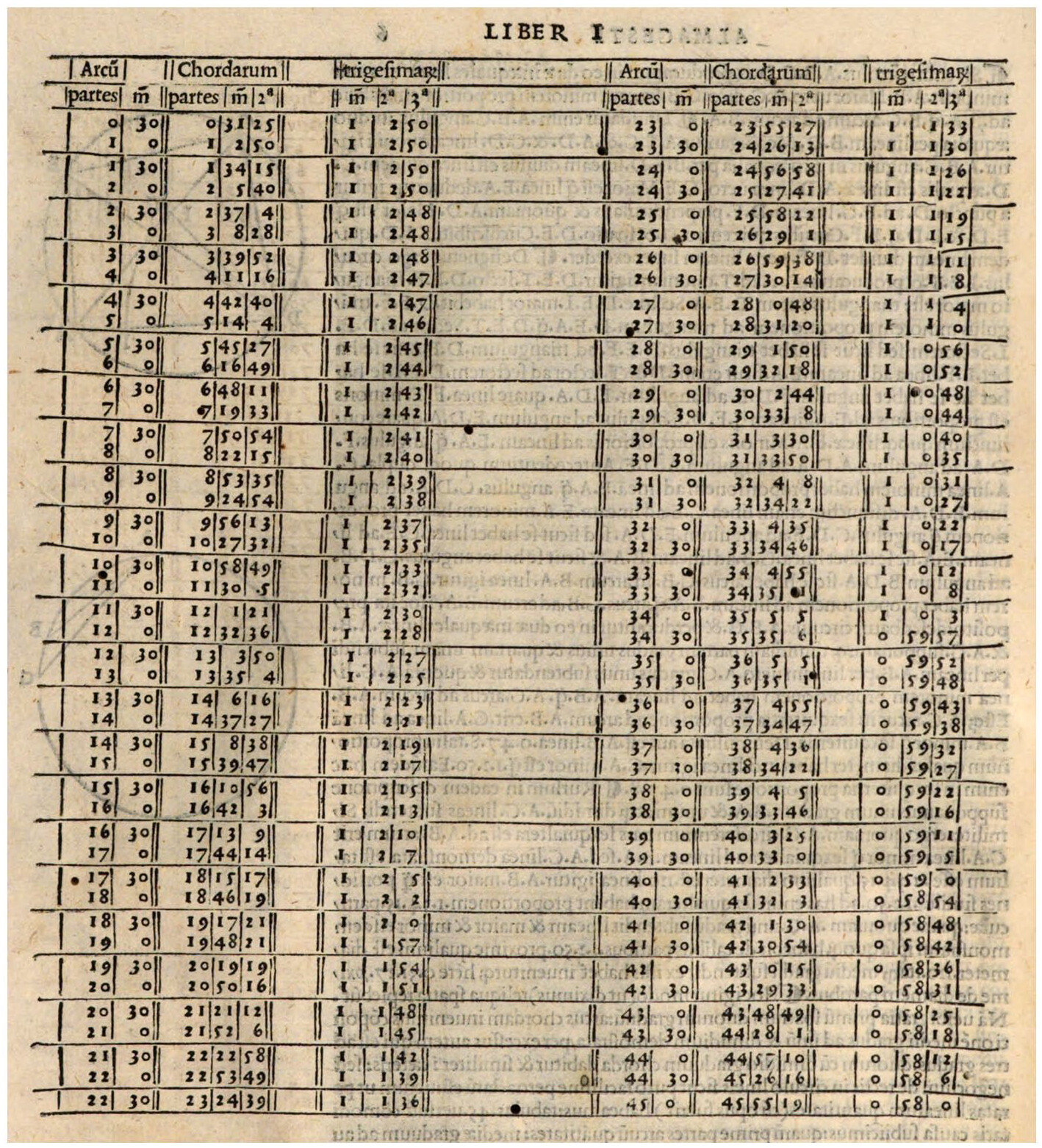
Убедительные доказательства наличия книгопечатания у древних греков
Исходя из всего вышеизложенного становится ясно, что тригонометрия чуть младше пива (по историческим меркам), но совершенно непонятно, откуда синус-то возник? Сейчас узнаем.
Восток — дело тригонометрическое
Как вы наверняка знаете в мире существует много разных религий. И одной из этих разных религий является ислам. Помимо множества разных фетв (это такие форки ислама с разными наборами правил) существуют «Пять столпов ислама» — базовые принципы, которых должен, по идее, придерживаться каждый правоверный мусульманин.
Тут и пост в Рамадан, который в этом году кончился не так давно, и шахиды шахада, то есть что-то вроде декларация себя мусльманином слова, кстати, не просто так похожи; шахид это не только мучение за веру, но и свидетель на суде, к примеру и, конечно, намаз: ежедневные пять молитв. Намаз-то нас и интересует, ведь молиться нужно обратившись лицом к Каабе. Кстати, не всегда. Какое-то время мусульмане молились лицом к Иерусалиму, чтобы отделить мусульман от язычников всяких. И только в Медине Мухаммеду было видение о том, что молиться надо лицом к Каабе.
Кааба — это тот самый чёрный куб, который вы могли видеть на фотографиях с огромным количеством мусульманских паломников. А внутри чёрного куба лежит чёрный камень (серьёзно, так и называется), который с точки зрения мусульман когда-то был в раю и белым, а оказался на земле и, впитав в себя грехи людей, стал чёрным. С точки зрения не мусульман это то ли метеорит, то ли ещё что-то в этом духе.
Кааба, если вдруг не видели

Которая впечатляет и сейчас
Само происхождение, впрочем, нас интересует мало, нам нужно знать только то, что направление на Каабу настолько важно, что имеет собственное название: кибла. И если сейчас вопрос определения киблы достаточно прост (достаточно запустить приложение, например), то, скажем, тысячу лет назад как с приложениями, так и с телефонами была достаточно напряжённая ситуация, которая стала исправляться совсем недавно. У людей, живущих в 2023 году, возникает резонный вопрос: если проблему нельзя решить с помощью телефона, то можно ли её решить вообще? Оказывается, можно.
Простым мусульманам, в целом, решить её просто: достаточно запомнить ориентацию в пространстве ближайшей мечети (впрочем, и в XXI веке с этим случались проблемы). Но как быть, собственно, строителям мечети? Им-то смотреть не на что.
На этом моменте в мусульманской истории и появляется математика. Строители (да и в целом образованные люди) не были дурачками и вполне осознавали шарообразность Земли. Что удивления вызывать не должно, потому что об этом факте подозревали ещё античные греки, Аристотель например (иногда, конечно, кажется, что он успел отметиться во всех науках вообще). Спустя почти тысячу лет после него у людей, интересующихся темой, сомнений не было никаких. А уж сейчас, с появлением массового образования, сторонников гипотезы о плоской Земли не осталось вовсе. Короче говоря, появилась необходимость как-то определять направления с учётом вновь открывшихся обстоятельств шарообразности. Но как это сделать?
Учебников алгебры за 10–11 класс у мусульман как-то под рукой не оказалось, так что пришлось сначала придумать основы этих учебников. Не самим по себе, конечно, с упоминавшимся уже «Альмагестом» они были знакомы, да и у индийцев достижения подсмотреть тоже были не дураки. Но стоит отдать должное в том, что сферической тригонометрией им пришлось заниматься более-менее самостоятельно, хоть и стоя на чьих-то плечах. Так, например, они вполне себе использовали теорему Менелая, а Аль-Бируни работал
Вот с такими вот
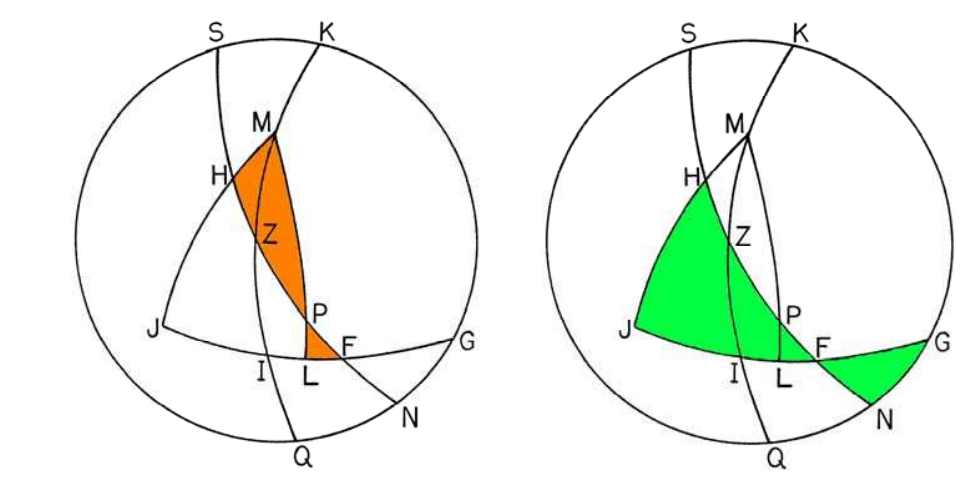
Сферическими треугольниками.
Насколько я понял современный английский перевод со средневекового арабского, Аль-Бируни в задаче строит небесную сферу, на которую смотрит снаружи. Зенит (для наблюдателя, не для Каабы), то есть наивысшая точка небесного свода, как водится, в центре, а горизонт, ну по краям. Где ж ему быть ещё.
На рисунках выше Z и M — зениты наблюдателя и Мекки соответственно; ZPN и MPL — соответствующие им меридианы, где P — небесный полюс; MZQ — это большой круг, проходящий через эти зениты, с полюсом в точке G (тут позволю себе напомнить, что в смысле сферической тригонометрии полюс — одна из двух точек пересечения перпендикуляра из центра сферы к плоскости большого круга); JLG и JHM — горизонты M и F соответственно. В этом методе предполагается, что мы знаем значение широты наблюдателя и Мекки, а также их разность долгот; они измеряются как PN = φZ, PL = φM, а MPZ = ΔL. Кибла, отсчитываемая от южного меридиана наблюдателя, равна q = ∠SZM = SK (честно говоря тут происходит какая-то сферическая магия, которую я не до конца понимаю; желающие могут углубиться в тему тут).
Подводя итоги
Так откуда синус-то взялся? Теперь, пройдя (довольно быстро, надо сказать) путь от египтян в мусульмане через греков можем более-менее предметно ответить на этот вопрос. Даже с разных точек зрения.
В смысле самого слова вполне латинское sinus («впадина» или «кривизна») оказывается переводом арабского «джайб» («карман» или, собственно, «впадина»). «Джайб» пришёл в арабскую математику из индийской, где словом «Джья» называлась тетива, а индийские же математики обозначали им то, что мы сегодня называет хордой.
В смысле самой функции понимание чего-то такого было ещё у греков, но в виде, который нам не вполне привычен сейчас. С появлением практической необходимости мусульмане подсмотрели что-то у греков, что-то у индусов и заморочились над сферической тригонометрией и навводили всякого.
Впрочем, до строгой формализации языка математики было ещё очень долго. Если не верите, то загляните вот в эту публикацию на хабре: во-первых она сама по себе хороша, а во-вторых там масса примеров того, как математики записывали результаты своей работы до наших цивилизованных времён.
Так или иначе, теперь вы сможете вполне обосновано отвечать на вопрос откуда эти синусы взялись. Не повод ли это подписаться на мой телеграм-канал?
