Этажи: 3D-навигация на WebGL в 2gis.ru

В 2014 году 2ГИС выпустил Этажи — это фича, позволяющая посмотреть схему этажей здания и найти на ней нужную организацию. Долгое время она существовала только в мобильных приложениях 2ГИС. Теперь эта возможность появилась и в онлайн-версии.
Этажи для веба сделаны на технологии WebGL: они полностью трёхмерные, их можно крутить и приближать. Это первый проект компании, сделанный на этой технологии, и мы хотели бы поделиться опытом реализации.
Технологический стек
Технология WebGL, позволяющая делать полноценную трёхмерную графику с аппаратным ускорением в браузере, быстро набирает популярность в веб-картографии. В качестве удачных примеров её применения можно привести уже упомянутые здесь Google Maps, а также библиотеку Mapbox GL.
Преимущество карт, сделанных на WebGL, в более плавных переходах и анимациях, а также в возможности гибко управлять внешним видом карты. Например, гугл-карты умеют рисовать на земле тени от домов, форма и размер которых соответствуют текущему времени суток. Очевидно, что в традиционных веб-картах, работающих на тайлах, это невозможно: однажды отрастрированные тайлы уже никак не поменяешь, их можно только показать как есть.
Недостаток WebGL — в большой сложности и высоком пороге вхождения. Поэтому, несмотря на то, что технологии уже 5 лет, популярность её до сих пор невысока. Мы давно хотели опробовать WebGL на какой-нибудь не самой сложной задаче, и Этажи стали отличной возможностью это сделать.
Наш проект состоит из WebGL-приложения, встроенного в онлайн-версию 2ГИС, и бэкенда, который раздаёт ему данные. При заходе в Этажи приложение загружает с бэкенда данные и отрисовывает по ним здание.
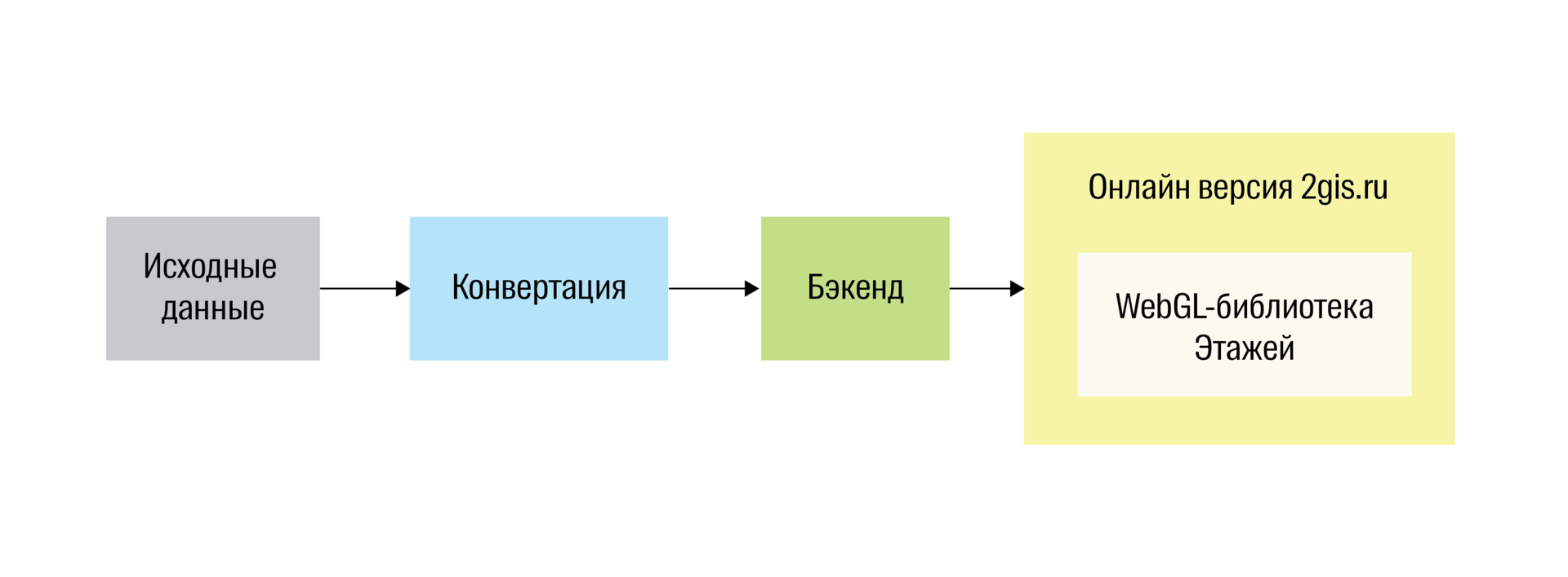
Схема архитектуры Этажей
В исходном виде данные представляют собой набор обычных WKT-геометрий — площадей-комнат, линий-стен и точек-POI. В таком виде для отрисовки в WebGL они не годятся, поэтому их нужно сначала подготовить: мы убираем из них всё лишнее, придаём плоским геометриям объём и всё триангулируем. Все эти операции выполняются на сервере. Для этого у нас написано отдельное приложение конвертации.
Работать с WebGL напрямую трудно: это низкоуровневое API, в котором для достижения самых простых вещей приходится писать много кода. В нашей вводной статье по WebGL описывается, как на чистом WebGL нарисовать вращающийся куб, и полный код получившегося примера занимает более 200 строк. Поэтому на раннем этапе разработки мы использовали популярный WebGL-фреймворк three.js.
Однако, three.js — тяжеловесный комбайн с огромным числом возможностей, из которых мы использовали лишь малую часть. Поэтому в определённый момент мы заменили его на собственноручно написанную библиотеку 2gl, в которой есть только то, что нам нужно.
Использование своей библиотеки уменьшило размер сборки приложения более чем в два раза и значительно повысило его производительность.
Как мы трудности преодолевали
Разработка WebGL-движка для рисования планов помещений — далеко не самая стандартная задача для фронтенд-разработчика. В ходе работы над Этажами нам пришлось решить множество необычных, интересных и зачастую неожиданных проблем, о некоторых из которых мы решили написать в этой статье.
Как сделать плоское объёмным?
Когда мы начали работу над этажами и стали изучать формат исходных данных, оказалось, что они даже не трёхмерные. Форма каждого этажа представляется набором двухмерных площадных (комнаты) и линейных (стены) геометрий. Для плоского отображения этажей в мобильной версии 2ГИС такого формата достаточно. Нам же пришлось придумать, как придать этажам объём.
С площадниками проблем не оказалось: мы просто рисуем их в плоскости пола. А вот со стенами пришлось повозиться. Сначала мы попробовали просто брать линии и делать из них плоские стены нулевой толщины. Получилось некрасиво:

Ранний прототип Этажей с плоскими стенами
В реальном мире стены имеют толщину. То же самое нужно было сделать и в Этажах.
Итак, нужно по набору ломаных линий получить набор трёхмерных геометрий стен. В общем виде решение этой задачи нетривиально. Но мы решили пойти от простого и сначала попробовали реализовать самое простое и очевидное решение «в лоб».
- Находим все точки пересечения стен.
- Для каждой точки пересечения перебираем все пары стен, образующих углы.
- Для каждой такой пары измеряем угол между ними.
- Проводим биссектрису этого угла и откладываем на ней «угловую точку» — она станет внешней границей будущей утолщённой стены.
- Соединяем все угловые точки и получаем внешние контуры стен.
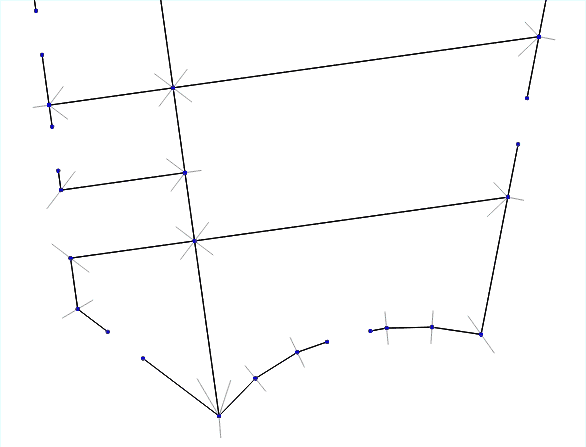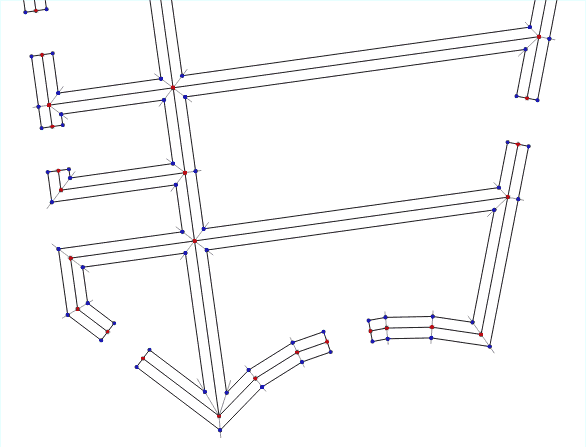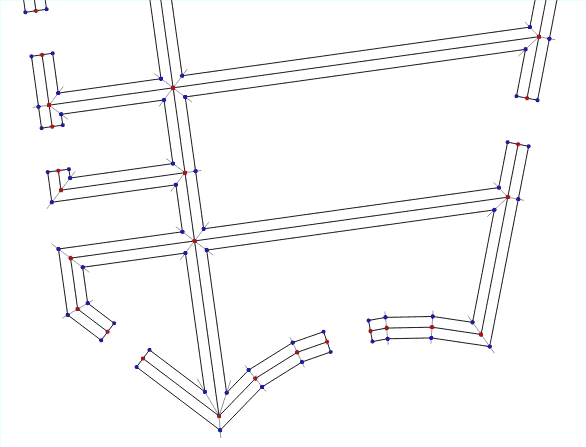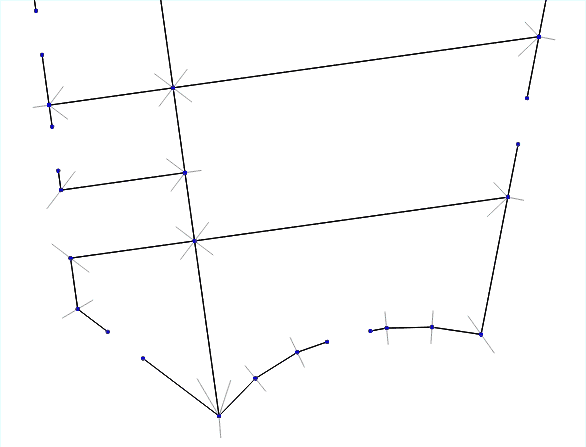
Анимация работы алгоритма для разной толщины стен
Этот простой алгоритм работает хорошо, только если требуется маленькая толщина стен. Если же стены нужно раздвинуть далеко, а особенно, если в данных при этом есть пересечения под острыми углами, результат уже будет некорректным:
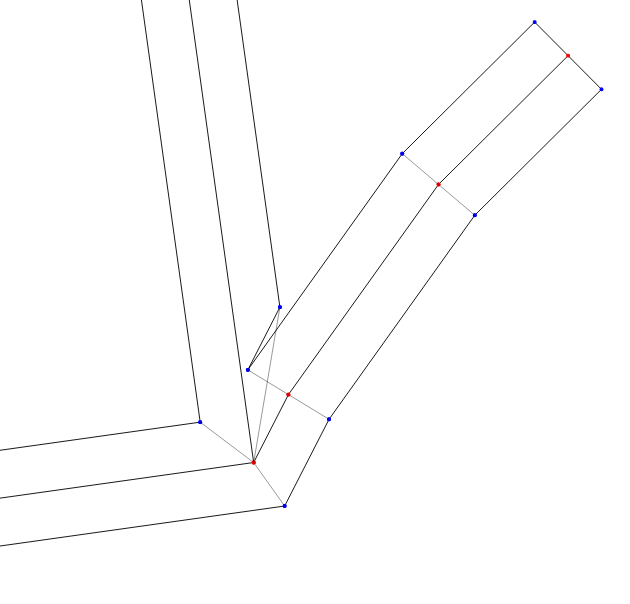
При большой толщине появляются артефакты
Однако, когда мы посмотрели на результаты его работы, оказалось, что на наших данных он даёт хорошие результаты в 100% случаев, поэтому придумывать что-то более сложное оказалось вовсе не нужно.
В результате мы получили в этажах красивые, объёмные стены, решив потенциально сложную задачу сотней строчек простого кода:
Стены теперь материальны
Как запрограммировать инерцию?
Ни один современный картографический движок не обходится без инерционного движения при перетаскивании карты. Благодаря инерции карта ведёт себя похоже на материальный объект, двигать её становится интуитивно просто и приятно. Инерция — одна из первых вещей, которую видит и испытывает пользователь, секунду назад открывший карту и начавший её двигать. Поэтому она вносит особенно большой вклад в общее впечатление от использования карты.
О том, как в общем устроена инерция в картах, можно почитать в этой статье. Описанное в ней решение имеет один недостаток: в нём анимация замедления полагается на периодический вызов специальной функции, которая на каждом кадре уменьшает скорость карты в определённое число раз. Такая реализация будет работать корректно только при постоянном FPS. Если же FPS просядет, то эта функция будет вызываться реже, и анимация продлится дольше, чем нужно.
Чтобы убрать зависимость от FPS, необходимо положение карты вычислять на основе времени, прошедшего с начала анимации. Вычислять его нужно по какой-то формуле.
Что это должна быть за формула? Первый ответ, который пришёл нам в голову — кинематическое уравнение равноускоренного движения из учебника физики за восьмой класс. Вот оно:
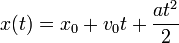
Здесь:
x0 — начальное положение
v0 — начальная скорость
a — ускорение
Идеально! x0 и v0 нам известно, а подобрав значение константы a, мы сможем анимацию настроить. А главное, что инерция, работающая по такой формуле, будет реалистичной и производить хорошее впечатление.
Так мы думали, пока не запрограммировали эту формулу. Оказалось, что она работает из рук вон плохо. При малых по модулю значениях ускорения ТЦ неконтролируемо уезжал за пределы экрана после малейшего движения мышью, будто машина на скользком льду, при больших — карта останавливалась почти мгновенно после драга.
Оба варианта создавали одинаково неприятное впечатление: в первом случае терялось чувство контроля, в втором создавалось впечатление плохо смазанного механизма. Золотую середину найти никак не получалось.
Устав от тщетных попыток подобрать оптимальное ускорение, мы попробовали использовать вместо физического уравнения одну из easing-функций Роберта Пеннера, которые уже много лет используются для js-анимаций и встроены во многие библиотеки.
Результат оказался великолепным: после драга карта плавно и грациозно останавливалась, при этом не уезжая слишком далеко. И несмотря на то, что движение её перестало быть «правильным» с точки зрения физики, восприниматься оно стало намного лучше.
Мы поэкспериментировали с разными easing-функциями и в итоге написали свою, которая работала уже в точности так, как нам хотелось, но это уже не самая важная часть истории. Важнее всего — простой урок, который мы усвоили: реалистичная анимация — ещё не значит хорошая анимация.
Как подписать комнаты?
Комнаты и объекты на этажах мы обозначаем с помощью маркеров и подписей к ним. Как нарисовать маркеры в рамках WebGL-приложения? Самое простое решение — создать для каждой из него по DOM-элементу и отображать их поверх WebGL-канваса. На каждом кадре необходимо вычислять новую позицию каждого маркера и передвигать соответствующие им DOM-узлы.
Нам пришлось почти сразу отказаться от этой идеи по одной простой причине: DOM — это слишком медленно. Необходимость обновлять позиции большого количества DOM-элементов на каждый кадр приводила к росту времени отрисовки кадра в десятки раз.
Выход один — использовать WebGL-спрайты. Достаточно нарисовать прямоугольник (а именно — два треугольника), натянуть на него нужную текстуру и поместить в 3D-сцену. Именно так, например, рисовались монстры в старых 3D-шутерах:
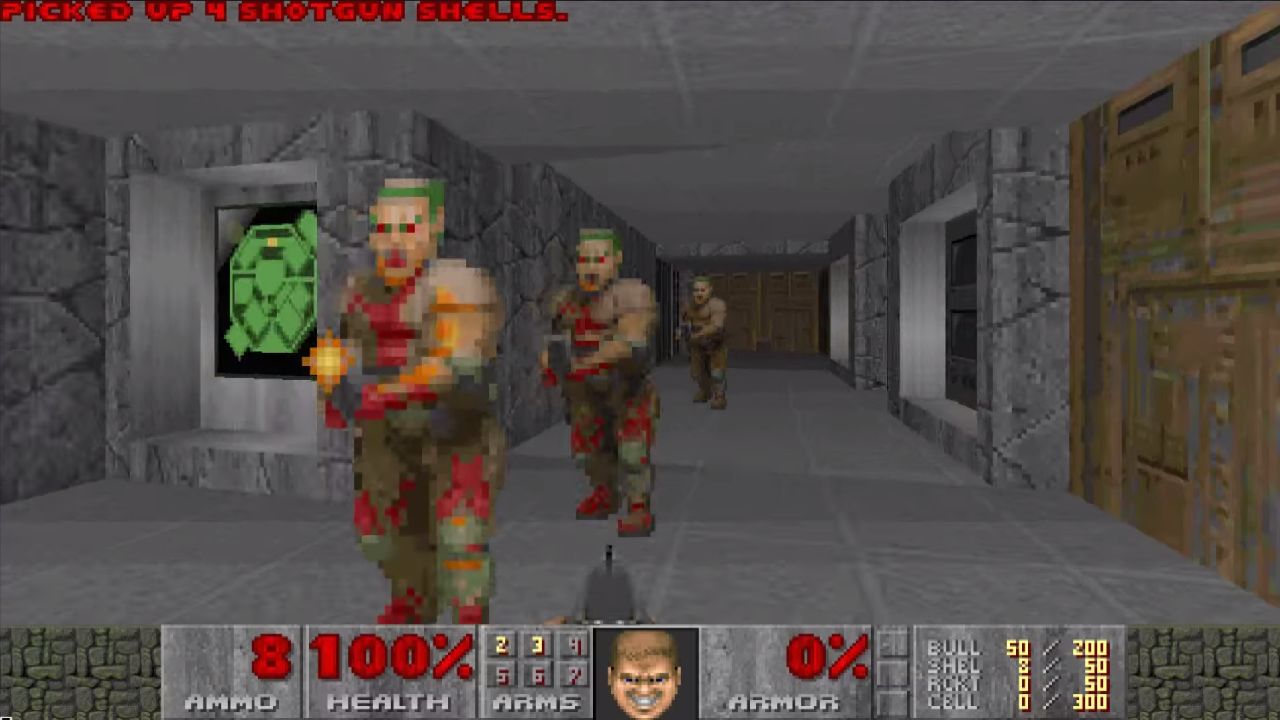
Почти то, что нам нужно
От зомби в Doom II маркеры в этажах отличаются только одной деталью: их размер не зависит от расстояния до камеры. Это требование легко реализовать с помощью кастомного вершинного шейдера: мы написали для маркеров специальный шейдер, который позиционирует вершины спрайта именно так, как нужно для сохранения постоянного размера в пикселях.
Отрисовка WebGL-спрайтов работает очень быстро: можно нанести на карту тысячи объектов без потери производительности. Но когда на карте слишком много маркеров, появляется следующая проблема: они перекрывают друг друга.
Что будет, если одновременно подписать все объекты этажа
Распространённым решением этой проблемы является кластеризация маркеров. Этот подход заключается в том, что среди множества всех маркеров выделяются группы наиболее близкорасположенных (кластеры), и при уменьшении масштаба кластер заменяется одним сборным маркером.
В этажах мы используем более простой подход, который мы назвали генерализацией: мы просто присваиваем каждому маркеру некоторый приоритет и скрываем маркеры с низким приоритетом, если они перекрывают более важные маркеры.
Для проверки пересечения маркеров нужно представить их в виде баундов — прямоугольных областей, которые они занимают на экране. А приоритеты мы выбираем на основе типа маркера: например, объекты инфраструктуры (лифты, туалеты и т. д.) имеют самый большой приоритет, поэтому они всегда будут видны даже на самых мелких масштабах.
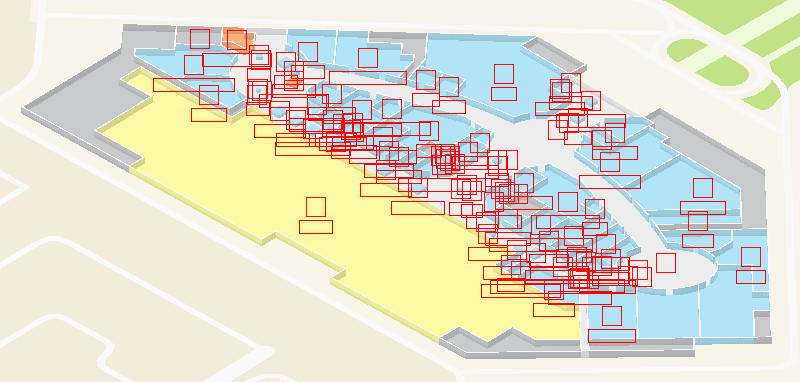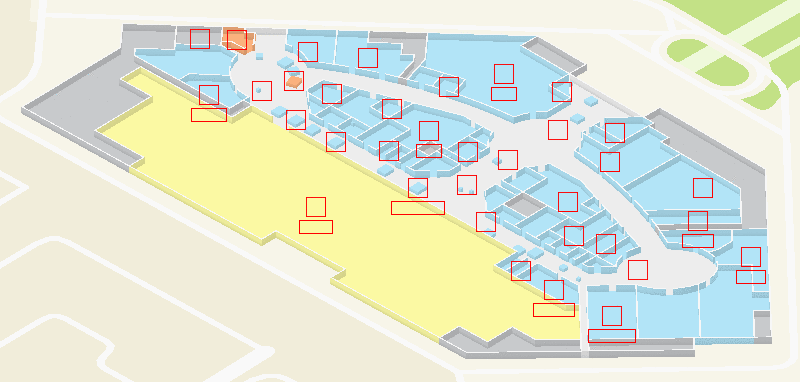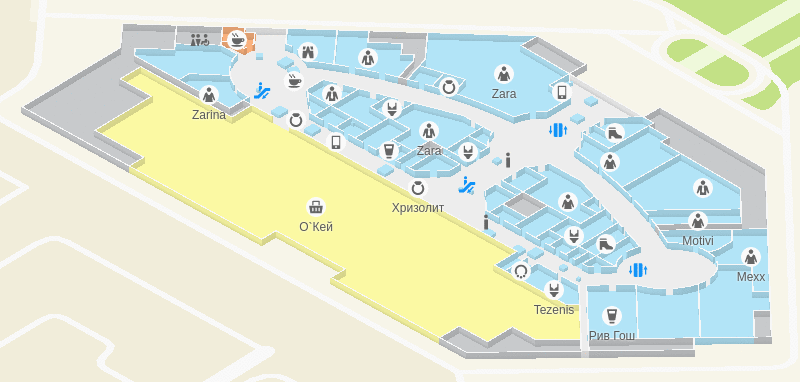
Работа генерализации: оставляем самое важное
Наивная реализация такого алгоритма имеет квадратичную трудоёмкость: каждый маркер требуется проверять на пересечение со всеми остальными. Чтобы он работал быстрее, мы применили прекрасную библиотеку rbush, реализующую структуру данных R-дерево. R-дерево умеет хранить прямоугольные области и быстро выполнять поиск их пересечений — это как раз то, что нам нужно.
После применения rbush трудоёмкость становится n * log (n), и на этажах Дубай Молла (до 1000 объектов на этаже) алгоритм отрабатывает за ~10 мс. Переместив его выполнение в веб-воркер, мы полностью исключили его влияние на FPS.
Последняя трудность в отрисовке маркеров на WebGL — сделать их кликабельными. У DOM-элементов есть события (click, mouseover и т. д.), на которые достаточно просто подписаться; в мире WebGL такого нет. Поэтому необходимо научиться по координатам курсора самостоятельно определять, в какой маркер кликнул пользователь.
Здесь нам на помощь опять приходит библиотека rbush: достаточно построить R-дерево, содержащее баунды всех видимых в данный момент маркеров, и для обработки клика просто выполнять по нему поиск. Поиск по R-дереву — логарифмическая операция, выполняется она быстро, и можно без проблем выполнять её не только по клику, но и по любому изменени положения курсора. Это позволяет сделать маркеры чувствительными не только к клику, но и наведению мыши.
Как сделать изометрию красивой?
Нетрудно заметить, что в Этажах используется изометрическая проекция, что для веб-карт довольно необычно.
Если для обычных трёхмерных карт лучше подходит привычная всем перспективная проекция, то схема помещения намного лучше смотрится в изометрии. В этой проекции далёкие объекты имеют тот же размер, что и близкие, благодаря чему карта становится более наглядной и по-хорошему схематичной. Более того, это просто красиво.
У изометрической проекции есть один недостаток: она неодинаково хорошо выглядит при разных углах поворота карты. Если повернуть камеру так, чтобы стены расположились на экране строго вертикально и горизонтально, получится такая картина:
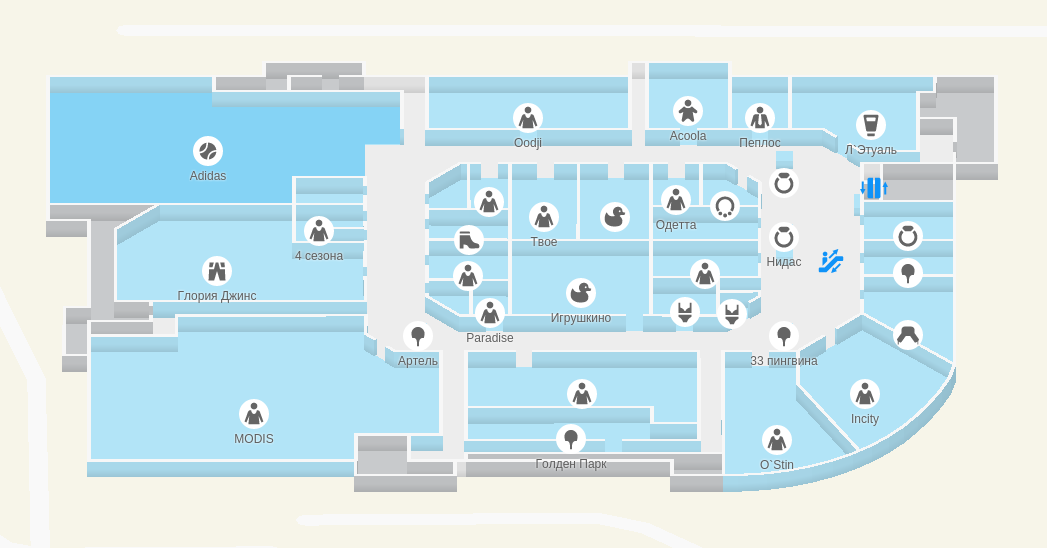
Неудачный угол поворота
Это не очень красиво: вертикальные стены оказываются почти невидимыми, карта читается плохо.
Изначально мы открывали все здания в дефолтном положении «север вверху», и торговые центры, у которых стены располагаются вдоль параллелей и меридианов, выглядели именно так.
Если же камеру немного повернуть и расположить стены именно так, как и положено в изометрии, получается так:
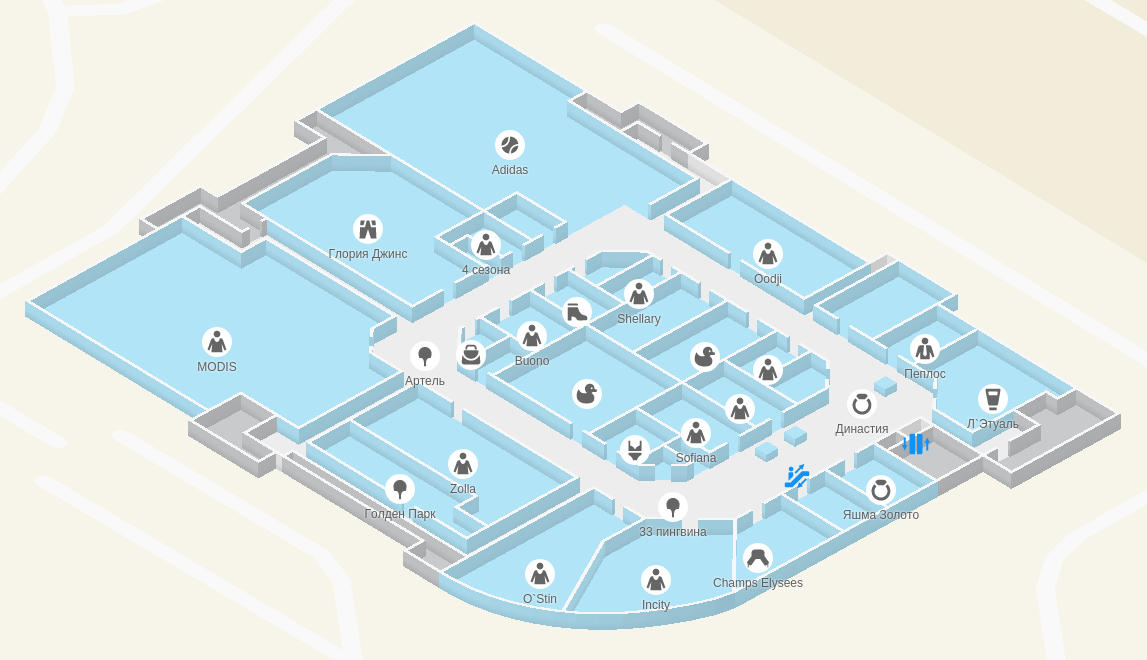
Удачный угол поворота
Намного лучше. Такой вид хорошо знаком нам по большому числу олдскульных (и не очень) игр, в которых используется изометрия:

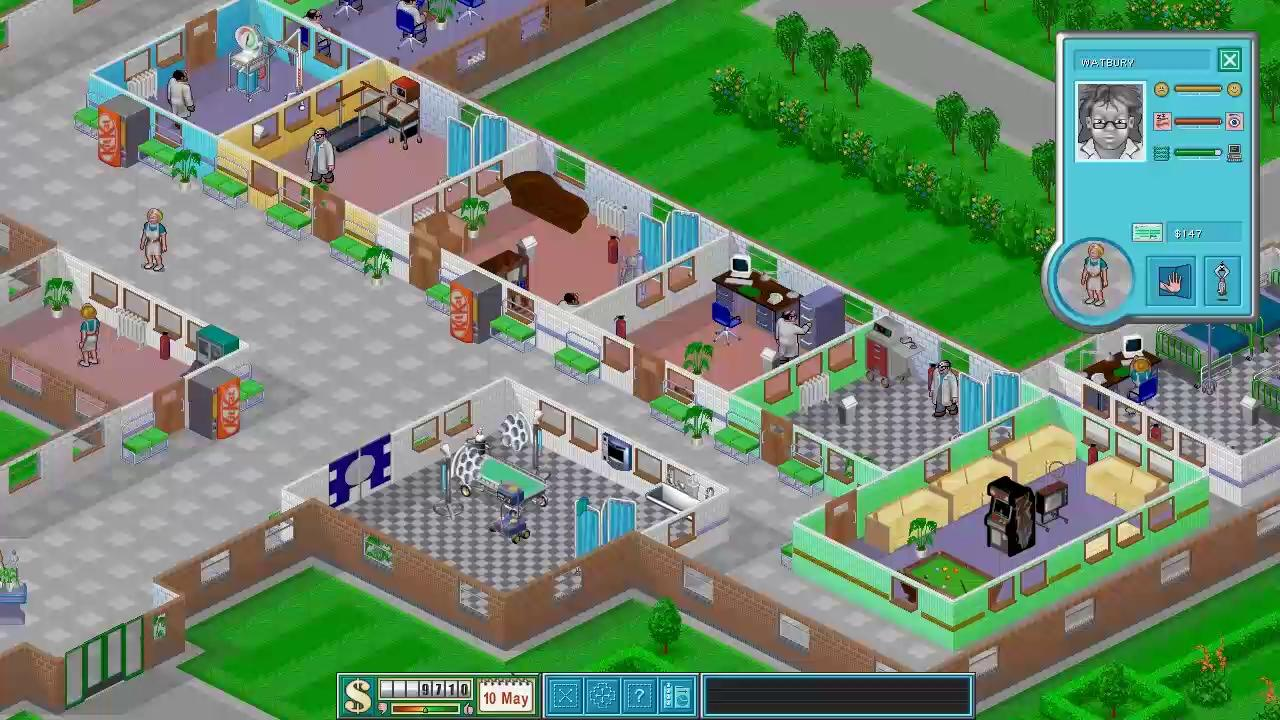
Fallout 2 и Theme Hospital
Таким образом, перед нами стояла задача для каждого торгового центра вычислить наиболее оптимальный угол поворота, чтобы при открытии режима этажей представить его в наилучшем виде.
Если архитектура помещений в изометрических играх, как правило, простая (все стены перпендикулярны), то с реальными зданиями всё не так просто: в наших данных имеются торговые центры очень причудливых форм, где стены пересекаются под самыми странными углами.
Однако, мы заметили, что даже в самых сложных по форме зданиях имеется некоторое направление, в котором расположено преобладающее большинство стен.
Этим фактом мы и решили воспользоваться. В математике такое преобладающее по частоте значение называется «модой». Мы попробовали при подготовке данных измерять углы каждой стены торгового центра и находить моду полученного множества. Прибавляя к найденной моде PI / 4, мы получали нужный угол поворота камеры.
Алгоритм показал прекрасные результаты: он безошибочно определяет «главное направление» стен и разворачивает по ним здание.
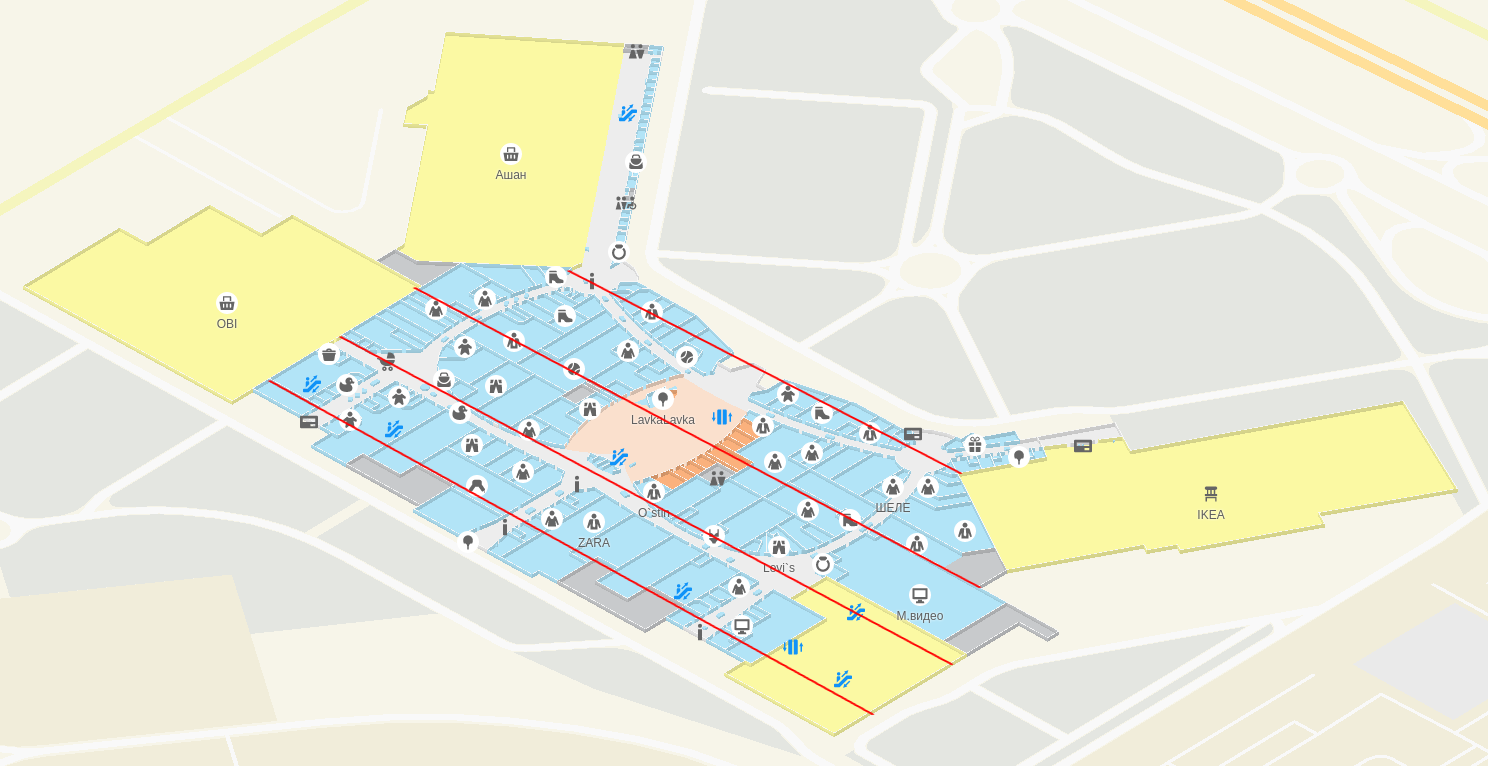
Правильно развёрнутый ТЦ «Мега Химки»
В математике, если множество содержит более одной моды, оно называется мультимодальным. Открывая разные здания на Этажах в 2ГИС, можно увидеть, что этот термин можно применить и к некоторым торговым центрам:
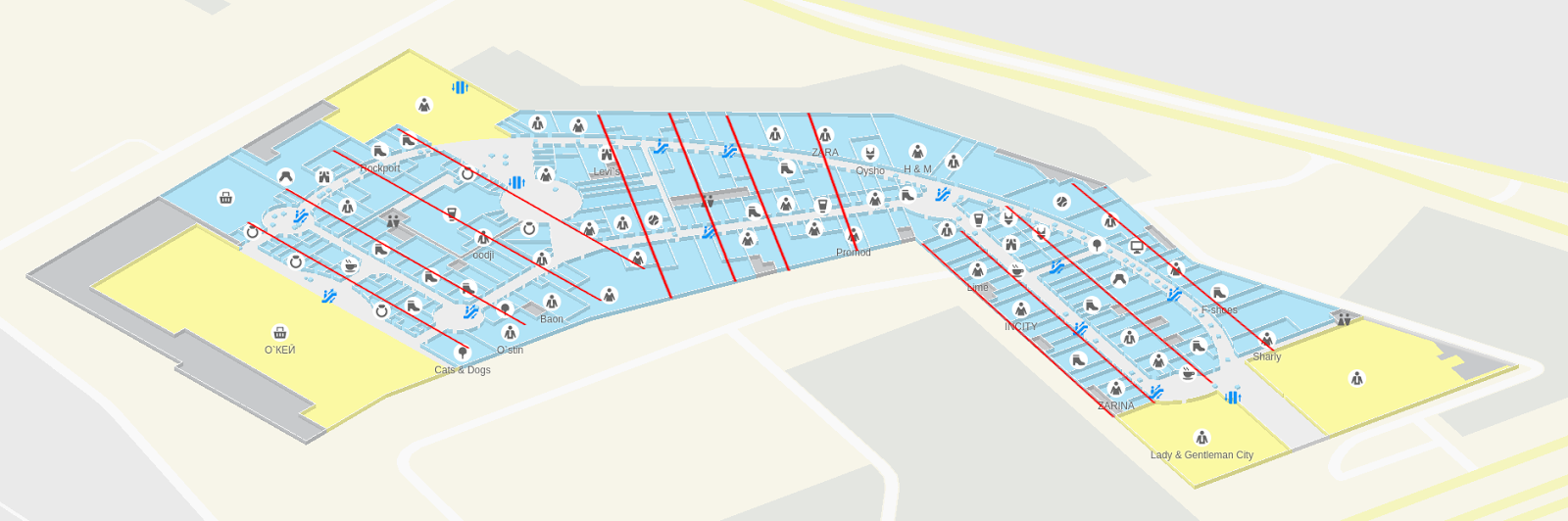
ТЦ «Золотой Вавилон» с тремя модами
Несмотря на то, что мод несколько, одна из них более модная. По ней мы и разворачиваем план ТЦ. Математика порой проявляется в нашей жизни в самых неожиданных формах, и это, пожалуй, один из таких случаев.
Выводы
Большую часть времени Этажи разрабатывались двумя программистами. Когда мы начинали работать над проектом, никто из нас ничего не знал ни о WebGL, ни о 3D-графике вообще, да и опыт веб-разработки у нас был довольно скромный.
Первые версии Этажей выглядели страшно и работали в лучшем случае на 20FPS. В ходе разработки мы набили все шишки, которые только могли набить, не раз целиком переписывали большие части проекта. Но результат каждый раз получался чуть лучше предыдущего, и это вдохновляло нас с самого первого прототипа, и вдохновляет до сих пор.
Не бойтесь пробовать WebGL: эта технология позволяет делать действительно фантастические вещи.
