Движение робота к точке с заданными координатами
Приветствуем вас, уважаемые хабравчане!
Наш научный коллектив, который носит название Студенческого конструкторского бюро кафедры СУиИ Университета ИТМО, продолжает разработку курсов по робототехнике, и хочет поделиться одним из последних проектов на Lego NXT.
Ранее мы публиковали курс «Практическая робототехника«на NXT. Сейчас этот курс используется для обучения студентов на кафедре, и на площадке «Открытое образование». Так же публиковались фрагменты этого курса с подробным описанием действий для идентификации модели двигателя и расчета регулятора для робота Segway.
В этот раз было решено реализовать объезд препятствий роботом с дифференциальным приводом. Конструкция робота достаточно простая: два колеса с двигателями, гироскоп и пара ультразвуковых датчиков. Для оценки пройденного расстояния используются энкодеры на валу двигателя, для ориентации робота, измеряется гироскопом его угловая скорость и рассчитывается угол поворота, а расстояние до препятствия измеряется ультразвуковыми дальномерами.
Стоит отметить, что робот перемещается за счет движения двух отдельно управляемых колес. А такая кинематическая схема имеет определенное математическое описание: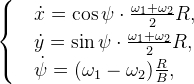 
где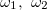 
— соответствующие угловые скорости вращения колес, x, y — соответствующие координаты, R — радиус колеса, B — расстояние между колесами.
В принципе движение в точку с заданными координатами можно решить использованием П-регулятора, но на практике этого будет недостаточно. Хотя в модели, представленной ниже все работает просто замечательно: 
Задача ставится следующим образом: робот должен достигнуть заданных координат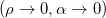 
.
При решении задач навигации мобильных роботов используются два основных подхода.
- Глобальный — определение абсолютных координат устройства при движении по длинным маршрутам. Траектория выбирается еще до начала движения на основе полученной информации.
- Локальный — определение координат устройства по отношению к некоторой (обычно стартовой) точке. Планирование задает лишь небольшой отрезок траектории, в конечной точке которого выбирается дальнейшая траектория.
Существует множество методов локальной навигации, например, такие как:
Остановимся подробнее на последнем методе. Поискав в сети информацию о способах управления подобным роботом, можно найти статью профессора кафедры теоретической кибернетики СПбГУ Матвеева А.С. и профессора Савкина А.В. из Университета Нового Южного Уэльса, Сидней, Австралия об алгоритме навигации робота среди движущихся и деформируемых препятствий. В статье авторы утверждают, что наиболее подходящим методом для решения нашей задачи является, собственно, метод тангенциального избегания, описанный профессором Федерального универститета Эспиринту-Санту, Витория, Бразилия Марио Сарцинелли, с которым мы имели честь познакомится во время поездки нашей команды в Бразилию.
Для начала опишем математическую модель, описывающую навигацию робота к цели, в полярных координатах: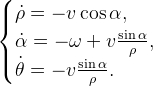 
Фактически, робот может полностью управляться с помощью значений угловой и линейной скорости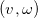 
, поэтому нужно найти такие их значения, чтобы выполнялось условие поставленной задачи 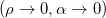. Для этого в статье предлагается воспользоваться аппаратом функции Ляпунова. Это будет квадратичная функция, включающая в себя расстояние до цели и курсовой угол: 
Производная по времени должна быть не положительна для того, чтобы расстояние до цели и курсовой угол не возрастали. Производная выглядит следующим образом: 
Выразив производную через математическую модель, предложенную выше, получаем: 
Эта производная отрицательно определена, если мы выберем в качестве управляющего воздействия следующие значения скоростей: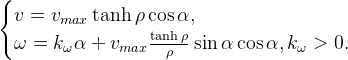 
Все это позволит роботу достичь своей цели, но пока лишь в отсутствии препятствий. Для избегания препятствий необходимо внести поправку в вычисление курсового угла: 
где 
— коэффициент пропорциональной составляющей курсового угла,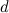 
— расстояние до препятствия, 
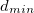— минимальное расстояние до препятствия.
С помощью вышеизложенного метода была реализовано движение из точки в точку с объездом препятствий. Результаты представлены на видео, погрешность обусловлена проскальзыванием колес.
Также мы добавили интегральную составляющую для расчет линейной скорости, чтобы компенсировать трение моторов. На видео ниже видно, что робот достаточно точно достигает цели в окрестности 3 сантиметра.
Ниже приведен пример итоговой программы на си-подобном языке NXC:
#define RAD_WHEEL 0.028 // радиус колес
#define DEG2RAD PI / 180
#define LEFT OUT_C
#define RIGHT OUT_B
#define GYRO S1
#define LIMIT 20 // предельное растояние до препятствия
#define K_I 50 // коэффициент интегральной составляющей линейной скорости
#define K_P 0.1 // коэффициент пропорциональной составляющей курсового угла
#define ERROR 0.03 // точность достижения целевой точки
task main() {
int rotA, rotB, // показания энкодеров
pwmLeft, pwmRight, // ШИМ для управления
distS3, distS2, distMax, kDist, // ошибки расстояния до препятствия
currentTime, previousTime, dt, // время
gyroSpeed, gyroOffset, // угловая скорость с гироскопа и ее калибровка
fileSize = 30640;
float course, courseAngle, bearing, // курс (psi), курсовой угол (alpha), пеленг (theta)
xCoord, yCoord, // координаты точки между колесами
delthaX, delthaY, // отклонения
length, intLength, // длина оставшегося пути, интеграл длины
path, prevPath, delthaPath, // путь пройденный точкой между колесами
xRef = -1, yRef = 0, // координаты точки назначения
baseSpeed = 0, control = 0, // линейная и угловая скорость
k = 20;
string s; // строка для формирования вывода
byte handle;
// инициализация датчиков
SetSensorLowspeed(S2);
SetSensorHTGyro(GYRO);
// создание файла для записи данных, задержка
DeleteFile("data.txt");
CreateFile("data.txt", fileSize, handle);
Wait(50);
// калибровка гироскопа, угловая скорость (град/сек)
gyroOffset = SensorHTGyro(GYRO);
course = 0;
previousTime = CurrentTick();
while (true) {
// измерение ошибки расстояния до препятствия
distS3 = LIMIT - SensorUS(S3);
distS2 = LIMIT - SensorUS(S2);
// определения положения препятствия (с какой стороны робота, далеко ли от него)
if (distS3 < 0 ) distS3 = 0;
if (distS2 < 0 ) distS2 = 0;
if (distS2 > distS3) distMax = distS2;
else distMax = distS3;
kDist = sign(distS2 - distS3);
currentTime = CurrentTick();
dt = currentTime - previousTime;
previousTime = currentTime;
// получение угловой скорости (град/сек)
gyroSpeed = SensorHTGyro(GYRO) - gyroOffset;
// расчет курса
course = course + gyroSpeed * PI * dt / 1000.0 / 180.0;
// снятие показаний энкодеров с двигателей
rotA = MotorRotationCount(LEFT);
rotB = MotorRotationCount(RIGHT);
// расчет пути пройденного точкой между колесами
path = (rotA + rotB) * DEG2RAD * RAD_WHEEL / 2;
// путь пройденный за один цикл программы
delthaPath = path - prevPath;
// сохранение предыдущего значения длины пути
prevPath = path;
// вычисление координаты X
xCoord = xCoord + delthaPath * cos(course);
// вычисление координаты Y
yCoord = yCoord + delthaPath * sin(course);
// вычисление отклонения по X
delthaX = xRef - xCoord;
// вычисление отклонения по Y
delthaY = yRef - yCoord;
// расчет пеленга
bearing = atan2(delthaY, delthaX);
// расчет курсового угла
courseAngle = bearing - course - K_P * kDist * distMax;
// разворот по кратчайшему углу
if (abs(courseAngle) > PI) courseAngle = courseAngle - sign(courseAngle) * 2 * PI;
// расчет расстояния до точки
length = sqrt (delthaY * delthaY + delthaX * delthaX);
intLength = intLength + length * dt / 1000;
if (intLength > 10) intLength = 10;
// расчет линейной скорости
baseSpeed = 100 * tanh (length) * cos (courseAngle) + K_I * intLength;
if (abs(baseSpeed) > 40) baseSpeed = sign (baseSpeed) * 40;
// расчет угловой скорости
control = k * courseAngle + sin(courseAngle) * baseSpeed / length;
// насыщение управляющего воздействия
if (abs(control) > 30) control = sign(control)*30;
// преобразование управления из float в integer, ШИМ в процентах
pwmLeft = baseSpeed + control;
// преобразование управления из float в integer, ШИМ в процентах
pwmRight = baseSpeed - control;
if (abs(pwmLeft) > 100) pwmLeft = sign (pwmLeft) * 100;
if (abs(pwmRight) > 100) pwmLeft = sign (pwmRight) * 100;
// подача управления
OnFwd(LEFT, pwmLeft);
OnFwd(RIGHT, pwmRight);
ClearScreen();
// вывод значений на экран NXT
NumOut(0, 8, distS3);
NumOut(0, 0, distS2);
// создание строки с данными
s = NumToStr(xCoord) + " " + NumToStr(yCoord) + " " + NumToStr(bearing) + " " + NumToStr(course);
// запись в файл
WriteLnString(handle, s, fileSize);
// выход при достижении области точки
if(abs(length) < ERROR) {
Off(OUT_BC);
break;
}
Wait(5);
}
}
Данная задача включена в дисциплину робототехники для первого и второго курса нашей кафедры, куда кроме нее входят segway, перевернутый маятник на тележке, маятник Капицы и трехзвенный манипулятор. Как видите, даже на таком простом оборудовании вполне можно разбирать серьезные робототехнические задачи.
