Дорожная карта математических дисциплин для машинного обучения, часть 1
Вместо предисловия
Допустим, сидя вечерком в теплом кресле вам вдруг пришла в голову шальная мысль: «Хм, а почему бы мне вместо случайного подбора гиперпараметров модели не узнать, а почему оно всё работает?»
Это скользкий путь — вы думаете, что достаточно пары вечеров с неторопливым чтением главки «Глубокого обучения» или 5-минутных youtube-роликов с различных MOOC; на деле, чтобы создать понимание, а не его иллюзию, требуется приличное количество времени (ну уж никак не меньше полугода для самых фанатичных);, но самое печальное — профит от этого мероприятия не очевиден — к счастью (или к сожалению), мир не устроен по законам математики, и будь вы трижды доктором физмат наук — некоторые модели всё равно будут работать лучше только в том случае, если вы подкинете в них побольше предобработанных данных либо соорудите огромный ансамбль.
Я считаю своим долгом вас предупредить, что это кривая дорожка, и возможно, что вложения в математику окупятся не так скоро, как того бы хотелось. Но математика интересна сама по себе, безотносительно приложений. Тем более что если вас заинтересовало, а что же происходит в этом черном ящике с гиперпараметрами, то это означает, что математика вам, скорее всего, не безразлична.
Ещё кое-что про мои рекомендации: я не люблю математическую литературу, которая кишит индексами, перлами типа «a_ijk с тремя подчеркиваниями и шляпкой сопряженное». Я считаю, что идеи важнее строгих выводов. При этом идеи не должны скатываться до «рукомаханий», всё должно быть довольно строго. Я не люблю книги наподобие Бурбаки и Кнута. На мой взгляд, эти книги предназначены для чего угодно, но не для чтения и не для изучения предмета. Они хороши в качестве ссылок и как энциклопедии.
Напоследок приведу кое-что из Бертрана Рассела:
Евклид презирал практическую полезность, которую внедрял Платон. Говорят, что один ученик, прослушав доказательства, спросил, что выиграет он изучением геометрии; тогда Евклид позвал раба и сказал: «Дай молодому человеку грош, поскольку он непременно должен извлекать выгоду из того, что изучает».
Теперь перейду собственно к основной части.
Пререквизиты
- Я предполагаю, что вы более-менее ориентируетесь в школьном курсе математики.
- Я предполагаю, что вы с английским не совсем на «вы», поскольку много дельной литературы и курсов написаны и рассказаны именно на этом языке. Математический английский не такой страшный, как английский вообще; это довольно ограниченный лексикон со стандартно построенными предложениями, без мешанины времён, без буйства красок и т.д.
- Я предполагаю, что у вас есть верёвка, которой вы можете привязать себя к стулу.
Уровни сложности
Не секрет, что по каждой математической дисциплине написано много литературы, и иногда проблемой становится даже простой выбор нужной книги. Я буду выделять несколько уровней сложности в литературе, что вы знали, куда стоит соваться, а куда лезть (пока что) не надо (или к чему можно обратиться для более полной информации).
- Bring it on — основная рабочая лошадка; это книги, что называется, «must have».
- Hurt me plenty — уровень повыше, позволяет оглядеть с высоты птичьего полёта уровень 1, систематизирует знания, объединяет различные области знаний.
- Nightmare — для сильных духом, уровень мехмата, для любителей математики и башен из слоновой кости.
Дорожная карта
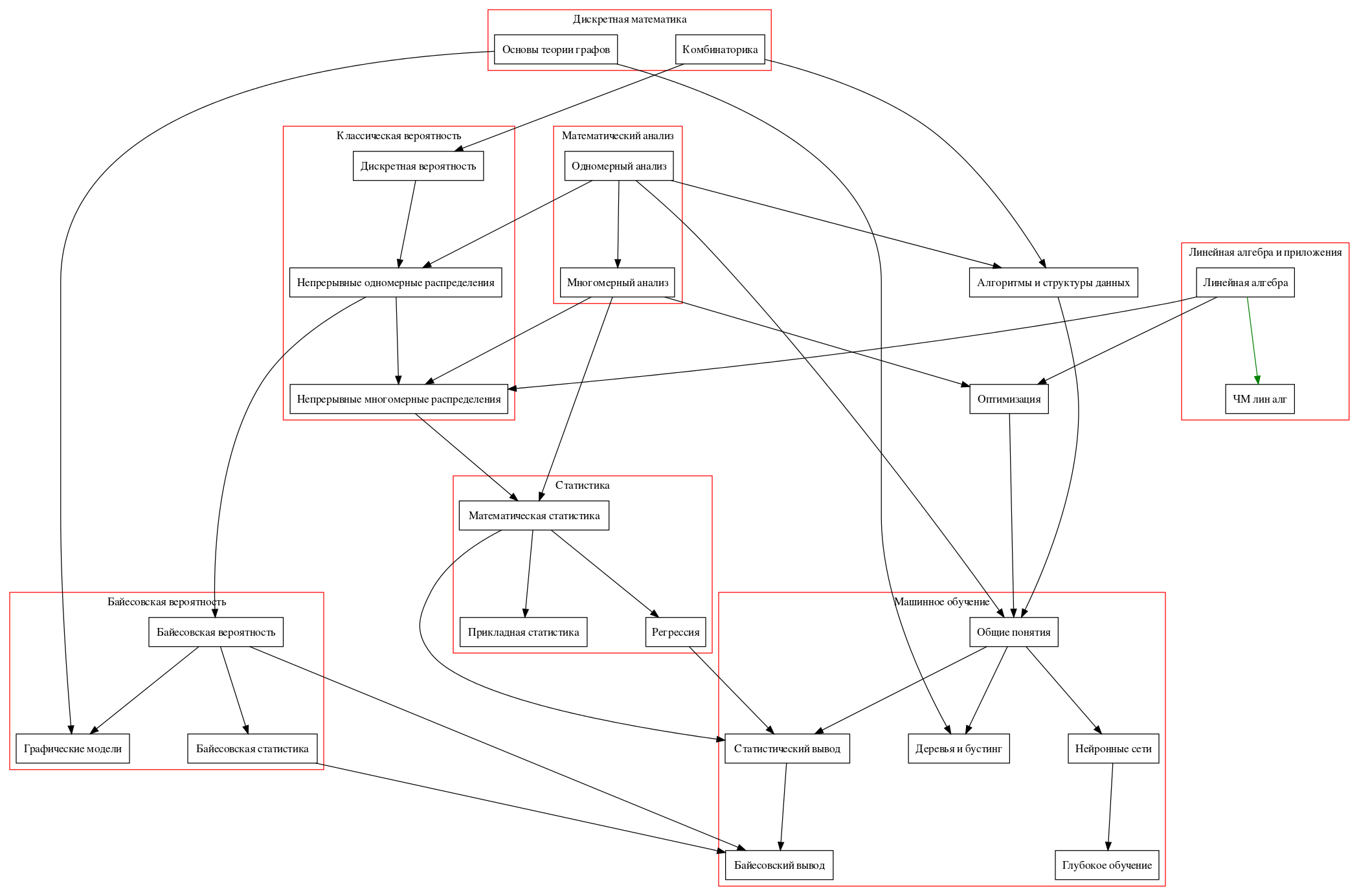
Перейду собственно к конкретным курсам.
Анализ, он же calculus
В российских вузах его преподают довольно интересно: большинство через несколько лет после окончания курса помнят смутно лишь какие-то там интегралы, и кажется что-то ещё. И это при том, что анализ — дисциплина прямо-таки одна из основополагающих в математике вообще. Мостиков от теории к практике как правило нет, и этот курс, подобно летающему острову парит где-то в головах, абсолютно оторванный от реальной жизни. Преодолевать это надо решением задач, причем не только из области математики, но и желательно что-либо из «реальной жизни».
Что нужно знать из анализа?
Основные вещи, которые нам понадобятся — понятие предела, непрерывности, производной, функции многих переменных, градиента, интеграла, интеграла с переменным верхним пределом, многомерного интеграла*.
Литература
Bring it on: тут всё более-менее стандартно — Пискунов / Фихтенгольц.
Hurt me plenty: Зорич, том 1. Эту книгу я люблю очень-очень сильно; это не учебник, но роман в формулах, что-то наподобие Евгения Онегина. К сожалению, он сложнее стандартных курсов по анализу за счет того, что многие вещи в нём даются более общО, и к этому надо привыкнуть; зато за счёт этой общности связываются воедино многие разрозненные вещи (см. те же пределы по базе).
Nightmare: Зорич том1 + том2, Рудин «Основы математического анализа», Львовский «Лекции по математическому анализу», Ramanan «Global Calculus».
В общем и целом резюме тут такое: литературы по анализу даже на русском языке полно; учебники чаще тяготеют к чисто математическим. В качестве дополнения к учебникам уровня 2–3 могу посоветовать несколько курсов:
Курсы из лектория МФТИ по анализу я не смотрел, но для полноты картины тоже приведу:
Практика
Практиковаться и применять полученные знания не то что «опционально», но строго-настрого ОБЯЗАТЕЛЬНО, иначе вся теория повиснет на вас мёртвым грузом, и вы быстро пойдете ко дну, причем даже не осознавая этого.
Предлагаю рассмотреть следующие варианты: Демидович, problem sets с курсов MIT (https://ocw.mit.edu/courses/mathematics/18–01sc-single-variable-calculus-fall-2010/index.htm)
Линейная алгебра
Хлеб насущный для Data Science и вообще для науки в целом. К сожалению, люди научились хорошо решать только линейные уравнения и их системы; для уравнений степени 2 и выше существуют всяческие очень нетривиальные теории (коммутативная алгебра, алгебраическая геометрия и иже с ними). Поэтому в анализе данных в основном применяются линейные модели (либо обобщенные линейные модели, как логистические регрессии, перцептроны и т.д.).
На русском языке много книг по линейной алгебре. Проблема в том, что они написаны либо для математиков, либо в них удручающе много индексов (и за деревьями не видно леса). Часто акцент в университетских курсах делается на жордановой форме; про другие стандартные формы часто не упоминается; есть Гаусс и бестолковый Крамер, но редко что бывает про LU, про SVD.
Что нужно знать из линейной алгебры?
Понятие вектора и векторного пространства; понятие линейного оператора; связь операторов и матриц; матричные разложения (LU, SVD как минимум); собственные вектора и собственные значения; ортогональные, унитарные операторы; симметричные и эрмитовы операторы; квадратичные формы, приведение к главным осям.
Литература
Bring it on: курс OCW-MIT Гилберта Стрэнга по линейной алгебре + его книжка.
ocw.mit.edu/courses/mathematics/18–06-linear-algebra-spring-2010/index.htm
Самое хорошее в этом курсе — отсутствие «сложных» и довольно бестолковых теорем линейной алгебры, всяческих двойственных пространств, большое количество задач в книге, практико-ориентированный подход (не «что это такое», а «как это посчитать»). Более толковых курсов по линейной алгебре я ещё не встречал.
Hurt me plenty: Axler «Linear algebra done right»; Гельфанд «Лекции по линейной алгебре»; курс МФТИ lectoriy.mipt.ru/course/LinearAlgebra; Кострикин «Введение в алгебру, часть 2», Тыртышников «Матричный анализ и линейная алгебра».
Проблема книг и курсов с этого уровня сложности в том, что они теоретико-ориентированные. Есть линейные функционалы и двойственные пространства, но нет матрицы проекции на подпространство и практических способов вычисления собственных значений. Скорее всего, курсы с этого уровня придётся дополнять сильной практикой; к примеру, численными методами линейной алгебры.
Про последнюю книгу отдельно. На мой взгляд, это одна из самых удачных русскоязычных книг по линейной алгебре в том смысле, что она не очень сильно оторвана от практики; при этом в ней содержатся и всяческие «продвинутые» темы. Она в какой-то мере может заменить лекции Стрэнга полностью, но её надо дополнять простыми задачами на «набить руку». Задачки в этой книге есть, но они довольно суровые.
Nightmare: Кострикин-Манин «Линейная алгебра и геометрия», Шафаревич-Ремизов «Линейная алгебра и геометрия».
В целом, на русском есть много хорошей литературы, особенно на последнем уровне, но она страдает излишней сложностью.
Практика
Как и в первом случае, практика обязательна. Проходите SVD — изучите сжатие изображений. Проходите матричные умножения — изучите быстрое преобразование Фурье, алгоритм Штрассена; решайте много задач (например, из задачников Кострикина либо Проскурякова); напишите своё LU-разложение, Гаусса. Для самых упорных я могу предложить замечательные книги по численным методам линейной алгебры, такие как Trefethen, Bau «NUMERICAL LINEAR ALGEBRA»; Хорн, Джонсон «Матричный анализ». Эти книги будут полезны, во первых, для «набития» руки; во-вторых, станет сразу понятно, что многие теоретические методы разбиваются в щепки о прозу жизни (машинная точность, нестабильность методов, работа с разреженными матрицами).
Дискретная математика
Ещё один кит современной CS. Здесь нас в основном будет интересовать комбинаторика и основы теории графов.
Что нужно знать из комбинаторики и теории графов?
Биномиальные коэффициенты, их асиптотика; графы; деревья; поиск в глубину и ширину; реккурентные соотношения и их решения;
Литература
Bring it on: Андерсон Дж. «Дискретная математика и комбинаторика»; Хаггарти, Шлипф Дж., Уайтсайдс С. «Дискретная математика для программистов», Оре О. «Графы и их применение».
Две первые книги — прекрасные талмуды по дискретной математике, покрывают практически все вопросы, которые надо знать.
Hurt me plenty: Грэхем, Кнут, Паташник «Конкретная математика», Харари «Теория графов», Оре «Теория графов».
Nightmare: Сачков «Введение в комбинаторные методы дискретной математики», Омельченко «Теория графов».
Практика
Как правило, в учебники по комбинаторике включается большое количество задач; их надо прорешивать. По сути вся комбинаторика — это искусство решения различных задачек, нежели какая-то единая теория.
