Дополненная реальность на Qt04.09.2015 18:48

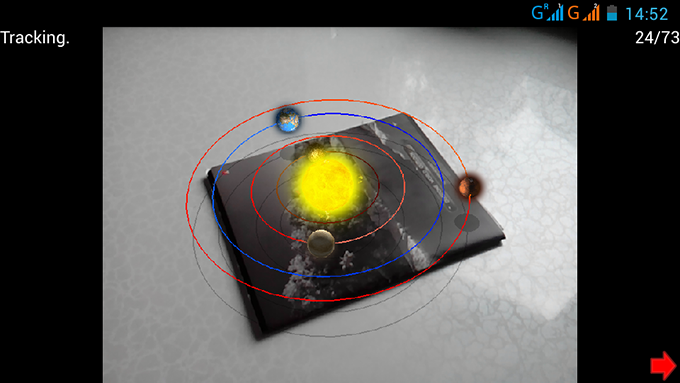
Сейчас дополненная реальность — это одно из самых интересных направлений. Поэтому я и взялся за ее изучение, а результатом этого стала собственная реализация кроссплатформенной безмаркерной дополненной реальности на Qt. Речь в этой статье пойдет о том, как это было реализовано (или же как это реализовать самому). Под катом можно найти демку и ссылку на проект на гитхабе.
Для работы дополненной реальности не требуется какие-либо маркеры, подойдет любая картинка. Нужно только выполнить инициализацию: направить камеру на точку на картинке, нажать кнопку старт и двинуть камеру вокруг выбранной точки.
Здесь можно скачать демки под Windows и Android (почему-то не работает на windows 10).

О проекте

Проект разделен на три части:
AR — здесь все что связано с дополненной реальностью. Все спрятано в пространство имен AR, ARSystem — главный объект системы, в котором и осуществляются все расчеты.
QScrollEngine — графический движок для Qt. Находится в пространстве имен — QScrollEngine. Есть отдельный проект на гитхабе.
App — собственно здесь описано приложение, использующее систему дополненной реальности и графический движок.
Все, что описано ниже основывается на проектах PTAM и SVO: Fast Semi-Direct Monocular Visual Odometry.Входные данные
Входными данными у нас является видеопоток. Под видеопотоком будем понимать в данном случае последовательность кадров, где информация от кадра к кадру меняется не очень сильно (что позволяет нам определить соответствия между кадрами).
В Qt определенны классы для работы с видеопотоком, но они не работают на мобильных платформах. Но заставить работать можно. Здесь описано как, в этой статье на этом останавливаться не буду.

Общий алгоритм работы

Чаще всего для работы дополненной реальности используются какие-то маркеры помогающие определять положение камеры в пространстве. Это ограничивает ее использования, так как, во-первых, маркеры должны быть постоянно в кадре, а во-вторых, их необходимо сначала подготовить (распечатать). Однако есть альтернатива — техника structure from motion, в которой данные о положении камеры находятся только по перемещению точек изображения по кадрам видеопотока.
Работать сразу со всеми точками изображения сложновато (хотя и вполне возможно (DTAM)), но для работы на мобильных платформах нужно упрощать. Поэтому мы просто будем выделять отдельные «особые» точки на изображении и следить за их перемещениями. Находить «особые» точки можно разными способами. Я использовал FAST. Этот алгоритм имеет недостаток — он находит углы только заданного размера (9, 10 пикселей). Чтобы он находил точки разного масштаба, используется пирамида изображений. Вкратце, пирамида изображений — это набор изображений, где первое изображение (основание) — это исходное изображение, а изображения следующего уровня в два раза меньше. Находя особые точки на разных уровнях пирамиды, находим «особые» точи разного масштаба. А сама пирамида используется также в оптическом потоке для получения траекторий движений наших точек. Прочитать про него можно здесь и здесь.

Итак, у нас есть траектории движения точек и теперь по ним надо как-то определить положение камеры в пространстве. Для этого, как можно понять из приложения, вначале выполняется инициализация по двум кадрам, в которых камера направлена примерно на одну и ту же точку, только под разными углами. В этот момент происходит вычисление положения камеры в этих кадрах и положение «особых» точек. Далее, по известным трехмерным координатам точек можно уже вычислить положения камеры в каждом следующем кадре видеопотока. Для более стабильной работы добавляем новые точки в процесс слежения, составляя карту пространства, которое видит камера.

Преобразование в экранные координаты

Для начала разберемся с тем, как трехмерные координаты «особых» точек переходят в экранные. Для этого используем эту формулу (обозначим ее, как формула 1):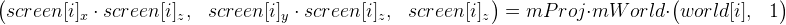

world[i] — это «особые» точки в мировых координатах. Чтобы не усложнять себе жизнь, предположим, что эти координаты не меняются на протяжении всего времени. До инициализации эти координаты не известны.
screen[i] — компоненты x и y — это координаты «особой» точки на изображении (их дает нам оптический поток), z — глубина относительно камеры. Все эти координаты уже будут своими на каждом кадре видеопотока.
mProj — матрица проекции размером 3 на 3 и имеет вид 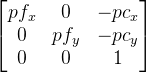, здесь pf — фокальное расстояние камеры в пикселях, pc — оптический центр камеры также в пикселях (обычно примерно центр изображения). Понятно, что эта матрица должна формироваться под параметры камеры (ее угол обзора).
mWorld — матрица, описывающая трансформацию точек, размером 3 на 4 (т. е. из обычная мировая матрица из которой убрали последнюю строчку (0 0 0 1). В этой матрице заключена информация о перемещении и повороте камеры. И это то, что собственно мы в первую очередь ищем на каждом кадре.
В данном случае не учитывается дисторсия, но будем считать, что она почти не влияет, и ею можно пренебречь.

Мы можем упростить формулу, избавившись от матрицы mProj (в формуле 1):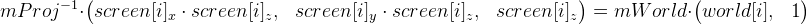

.
Введем 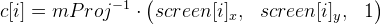, которые считаем заранее. Тогда формула 1 упрощается до  (пусть это будет формула 2).

Инициализация

Как уже говорилось, инициализация происходит по двум кадрам. Обозначим их как A и B. Значит у нас появятся матрицы 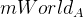и . Точки c[i] на кадрах A и B обозначим как cA[i] и cB[i]. Так как мы сами вольны выбирать начало координат, предположим, что камера в кадре A как раз там и находится, поэтому 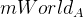 — это единичная матрица (только размером 3 на 4). А вот матрицу придется все-таки вычислять. И сделать это возможно при помощи точек, расположенных на одной плоскости. Для них будет справедлива следующая формула: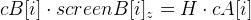
, где матрица H — это плоская гомография.
Перепишем выражение таким образом (убрав индекс i для наглядности):

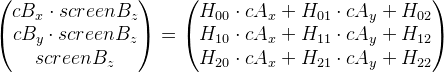
А теперь перейдем к такому виду, избавившись от :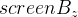

Представив матрицу H в виде вектора 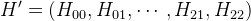, можем представить эти уравнений в матричном виде:

.

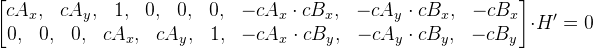Обозначим новую матрицу как M. Получим M * H» = 0. Все это расписывалось только для одной точки, поэтому в матрице M только 2 строки. Для того, чтобы найти матрицу H', необходимо, чтобы в матрице M было количество строк больше либо равно количеству столбцов. Если имеем только четыре точки, то можно просто добавить еще одну строку из нулей, выйдет матрица размером 9 на 9. Далее при помощи сингулярного разложения находим вектор H» (само собой он не должен быть нулевым). Вектор H» — это, как мы помним, векторное представление матрицы H, так что у нас теперь есть эта матрица.
Но как говорилось выше, все это справедливо только для точек, расположенных на одной плоскости. А какие из них расположены, а какие нет, заранее мы не знаем, но может предположить с помощью метода Ransac таким образом:

1. В цикле, с заранее заданным количеством итераций (скажем 500) выполняем следующие действия:
   
   • Случайным образом выбираем четыре пары точек кадров A и B.
   • Находим матрицу H.
   • Считаем сколько точек дают ошибку меньше заданного значения, т. е. пусть 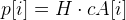и тогда должно выполняться условие — .
   
   
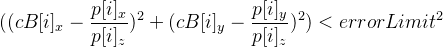2. Выбираем H на той итерации, в которой получилось больше всего точек.

Матрицу H можно получить используя функцию из библиотеки OpenCV — cvFindHomography.

Из матрицы H теперь получим матрицу перехода положения от кадра A к кадру B и назовем ее mMotion.
Для начала выполняем сингулярное разложение матрицы H. Получаем три матрицы: 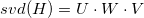. Введем заранее некоторые значения:
 — в итоге должно быть равно ±1;

Массивы (ну или вектора), указывающие нужный знак: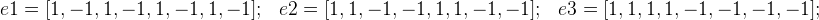

А дальше уже можем получить 8 возможных вариантов mMotion:

;

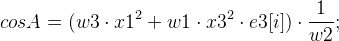
, где R[i] — матрица поворота,
t[i] — вектор смещения.

И матрицы 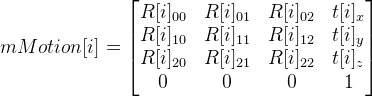. Параметр i = 0, …, 7, и соответственно получаем 8 вариантов матрицы mMotion.
Вообщем, мы имеем следующее соотношение: = mMotion[i] * 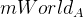, т. к.  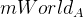— это единичная матрица, то выходит = mMotion[i].
Осталось выбрать одну матрицу из 8 ми mMotion[i]. Понятно, что если выпустить лучи из точек первого и второго кадра, то они должны пересекаться, причем перед камерой, как в первом, так и во втором случае. Значит, подсчитываем количество точек пересечения перед камерой в первом и во втором кадре используя получившиеся mMotion[i], и отбрасываем варианты, при которых количество точек будет меньшим. Оставив пару матриц в итоге, выбираем ту, которая дает меньше ошибок.
Итак, у нас есть матрицы 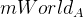и , теперь зная их можно найти мировые координаты точек по их проекциям.

Вычисление мировых координат точки по нескольким проекциям

Можно было бы воспользоваться методом наименьших квадратов, но на практике у меня лучше работал следующий способ:
Вернемся к формуле 2. Нам необходимо найти точку world, которую обозначим как a. Допустим у нас есть кадры, в которых известны матрицы mWorld (обозначим их как mW[0], mW[1], …) и известны координаты проекций точки a (возьмем сразу с[0], с[1], …).
И тогда имеем такую систему уравнений: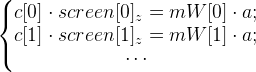

Но можно представить их в таком виде, избавившись от 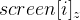 (подобно тому как делали ранее):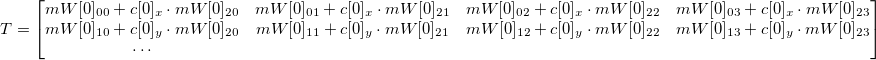

где s –любое число не равное нулю,
 — система уравнений в матричном виде. T — известно, f — необходимо вычислить, чтобы найти a.
Решив данное уравнение с помощью сингулярного разложения (также как нашли H'), получим вектор f. И соответственно точка .

Вычисление положения камеры используя известные мировые координаты точек

Используется итеративный алгоритм. Начальное приближение — предыдущий результат определения. На каждой итерации:

1. Ведем еще точки 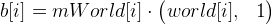. В идеале точки c[i] должны быть равны точкам b[i], на так как текущее приближение mWorld — это лишь пока приближение (плюс еще другие ошибки вычислений), они будут различаться. Подсчитаем вектор ошибки таким образом: 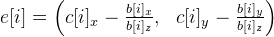. Решаем систему уравнений методом наименьших квадратов: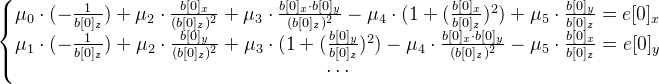
   

   Найти необходимо шестимерный вектор  — вектор експоненты.

2. Находим матрицу cмещения из вектора : dT = exp_transformMatrix (mu).
   
   Код этой функции:

   TMatrix exp_transformMatrix(const TVector& mu)
   {
       //Вектор mu - 6-мерный вектор 
       TMatrix result(4, 4);//создаем матрицу 4 на 4
       static const float one_6th = 1.0f / 6.0f;
       static const float one_20th = 1.0f / 20.0f;
       TVector w = mu.slice(3, 3);//получаем последние 3 элемента вектора mu 
       TVector mu_3 = mu.slice(0, 3);//получаем первые 3 элемента вектора mu
       float theta_square = dot(w, w);//dot - скалярное произведение векторов
       float theta = std::sqrt(theta_square);
       float A, B;
   
       TVector crossVector = cross3(w,  mu.slice(3));//cross3 векторное произведение 2х 3х-мерных векторов
       if (theta_square < 1e-4) {
           A = 1.0f - one_6th * theta_square;
           B = 0.5f;
           result.setColumn(3, mu_3 + 0.5f * crossVector);//устанавливаем 4ый столбец матрицы
       } else {
           float C;
           if (theta_square < 1e-3) {
               C = one_6th * (1.0f - one_20th * theta_square);
               A = 1.0f - theta_square * C;
               B = 0.5f - 0.25f * one_6th * theta_square;
           } else {
               float inv_theta = 1.0f / theta;
               A = std::sin(theta) * inv_theta;
               B = (1.0f - std::cos(theta)) * (inv_theta * inv_theta);
               C = (1.0f - A) * (inv_theta * inv_theta);
           }
           result.setColumn(3, mu_3 + B * crossVector + C * cross3(w,  crossVector));
       }
       exp_rodrigues(result, w, A, B);
       result(3, 0) = 0.0f;
       result(3, 1) = 0.0f;
       result(3, 2) = 0.0f;
       result(3, 3) = 1.0f;
       return result;
   }
   
   void exp_rodrigues(TMatrix& result, const TVector& w, float A, float B)
   {   
       float wx2 = w(0) * w(0);
       float wy2 = w(1) * w(1);
       float wz2 = w(2) * w(2);
       result(0, 0) = 1.0f - B * (wy2 + wz2);
       result(1, 1) = 1.0f - B * (wx2 + wz2);
       result(2, 2) = 1.0f - B * (wx2 + wy2);
       float a, b;
       a = A * w(2);
       b = B * (w(0) * w(1));
       result(0, 1) = b - a;
       result(1, 0) = b + a;
       a = A * w(1);
       b = B * (w(0) * w(2));
       result(0, 2) = b + a;
       result(2, 0) = b - a;
       a = A * w(0);
       b = B * (w(1) * w(2));
       result(1, 2) = b - a;
       result(2, 1) = b + a;
   }
   
   

   
   
3. Обновляем матрицу .

Достаточно 10–15 итераций. Тем не менее можно вставить какое-то дополнительное условие, которое выводит из цикла, если значение mWorld уже достаточно близко к искомому значению.
По мере определения положения на каждом кадре, какие-то точки будут теряться, а значит необходимо искать потерянные точки. Также не помешает поиск новых точек, на которые можно будет ориентироваться.

Бонус — трехмерная реконструкция

Если можно найти положение отдельных точек в пространстве, так почему бы все-таки не попробовать определить положение всех видимых точек в пространстве? В реальном времени делать это слишком затратно. Но можно попробовать сделать запись, а реконструкцию выполнить потом. Собственно это я и попробовал реализовать. Результат явно не идеален, но что-то выходит:

Ссылка на исходный код на github.

© Habrahabr.ru