Дифференциальные уравнения и продление жизни08.06.2021 00:31

188. Гектора ж, в бегстве преследуя, гнал Ахиллес непрестанно. Словно как пёс по горам молодого гонит оленя.<…> 199. Словно во сне человек изловить человека не может, Сей убежать, а другой уловить напрягается тщетно, — Так и герои, ни сей не догонит, ни тот не уходит.

Задача №1. Ахиллес и Смерть

В некоей альтернативной вселенной герою по имени Ахиллес предрекли, что жить ему осталось ровно m лет. Но мать Ахиллеса благодаря своему волшебству (она ж нимфа по легенде), продлевает ему жизнь таким образом, что каждые k (k > 1) лет продолжительность жизни увеличивается на 1 год. Сколько Ахиллес проживет в итоге, если считать, что увеличение происходит непрерывно?

Пусть x — это сколько осталось жить нашему герою. Ахиллес проживает первые m лет, но за эти годы получает $\frac{m}{k}$ лет прибавки к ПЖ. Он проживает эти $\frac{m}{k}$ лет, но за это время получает еще $\frac{m}{k^2}$ лет (прибавку разделить на k). И так далее, до бесконечности и можно подумать, что герой никогда не умрет. Но это не так: Смерть все таки догонит Ахиллеса, потому что все эти прибавки образуют бесконечную геометрическую прогрессию:

$x = m + \frac{m}{k} + \frac{m}{k^2} + \frac{m}{k^3} + ... = m(1 + \frac{1}{k} + \frac{1}{k^2} + \frac{1}{k^3}+ ... )$

И тут стоит обратить внимание на условие: k > 1 из чего следует, что $\frac{1}{k}<1$ а это значит, что геометрическая прогрессия бесконечно убывающая. А бесконечно убывающая геометрическая прогрессия сходится к конечному значению:

$x = \frac{m}{1 - \frac{1}{k}} = \frac{mk}{k-1}$ вывод формулы суммы бесконечной геометрической прогрессии

Пусть у нас есть вот такая сумма:

$S = 1 + q + q^2 + ... + q^{n-1}$

И тут кому-то пришла в голову гениальная мысль: «а что если обе части равенства умножить на q?». Так чего же мы ждем! Умножаем:

$qS = q + q^2 +q^3+ ... + q^{n}$

А теперь вычтем из первого второе и получим красивую формулу для суммы:

$S(1-q) = 1 - q^n => S = \frac{1-q^n}{1-q}» src=«https://habrastorage.org/getpro/habr/upload_files/187/d03/7e9/187d037e93b88b7241e10ccf2bbac521.svg» />Если q < 1, то при n стремящемся к бесконечности очевидно получаем:<img alt=$

Так как q^n стремится к нулю

В период с 2000 по 2019 год ожидаемая продолжительность жизни голландских мужчин, например, увеличилась с 75.5 до 80.5 лет (то есть примерно на год каждые четыре года), что согласуется с данными по Европе в среднем. Таким образом, если человеку на текущий момент осталось жить 40 лет, а ожидаемая ПЖ увеличивается на год каждые четыре года, то имеем:

$x = \frac{40 * 4}{4-1} \approx 53.3$

то есть мужчина-европеец в возрасте примерно 38 лет может прожить не 40 лет в среднем, а примерно на 13 лет дольше из-за прогресса в медицине (конечно, данные расчеты много чего не учитывают, нельзя их воспринимать как надежные предсказания).

А вот если k <= 1, то имеем уже бесконечность и это и есть та самая пресловутая longevity escape velocity о которой много говорит знаменитый борец со старением Обри Ди Грей. То есть Смерть никогда не догонит Ахиллеса.

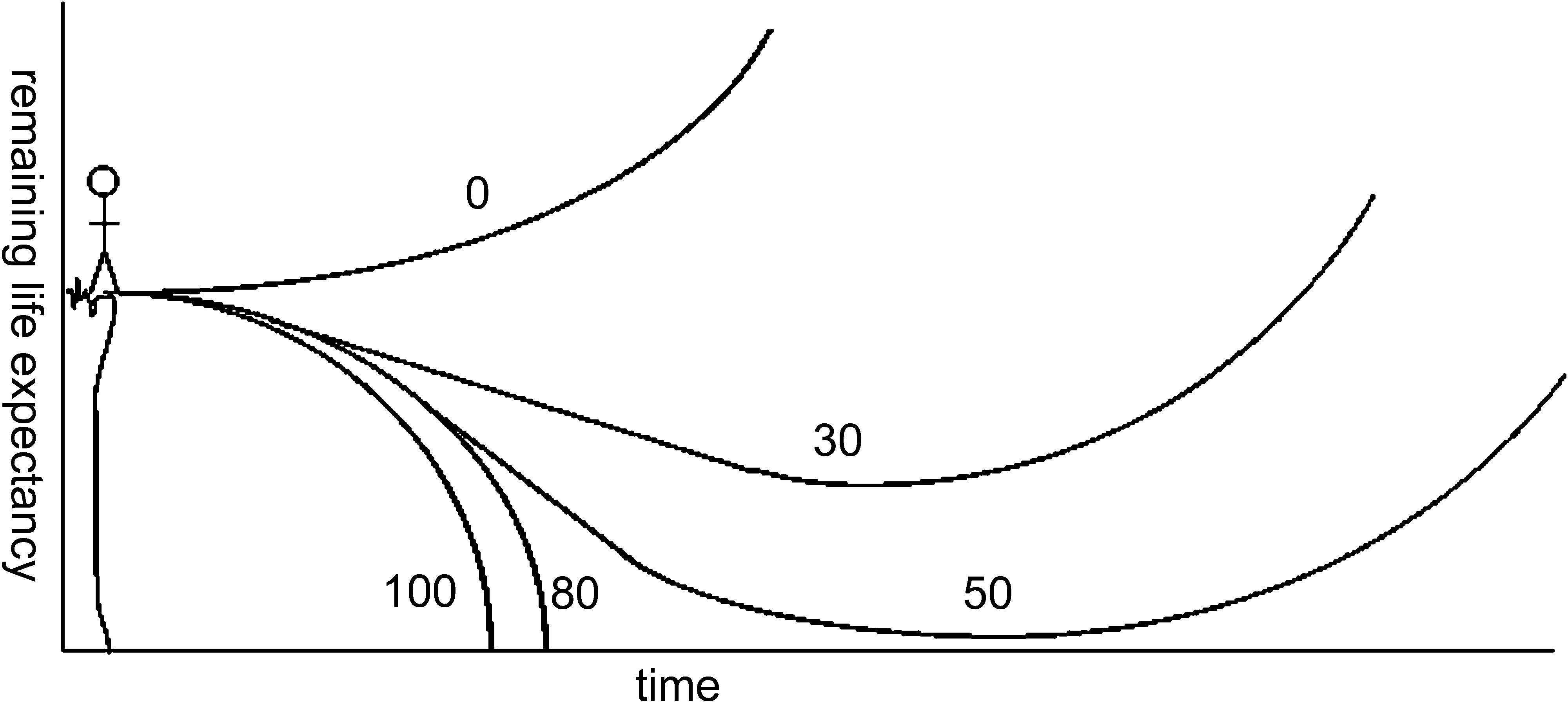
А теперь давайте посмотрим насколько эта же задача легче и логичнее решается при помощи дифференциальных уравнений:

$dx = -dt + \frac{dt}{k}$

dx — это насколько изменилось количество оставшихся лет до смерти за период dt. В отсутствии медицинского прогресса dx просто уменьшается на величину dt (логично, черт возьми). А прогресс добавляет определенное количество лет, такое что оно равно 1, если dt=k годам. Решается это уравнение тоже элементарно:

$\int{dx} = \int{\frac{dt}{k}} - \int{dt} => x (t) = \frac{t}{k} — t + C => x (t) = \frac{t (1-k)}{k} + C» src=«https://habrastorage.org/getpro/habr/upload_files/d27/034/6de/d270346dee64409efd75829ed369ab39.svg» />Совершенно очевидно, что x (0) = m, откуда C = m. А теперь подставим это в уравнение выше и выразим время t через которое Ахиллес помрет (x (t) = 0): <img alt=$ t = \frac{mk}{k-1}» src=«https://habrastorage.org/getpro/habr/upload_files/633/ea1/c3e/633ea1c3ed3fda6f8529296e5462f7d3.svg» />

Получилось просто и красиво, более того, есть задачи на которые можно дать ответ только с помощью дифференциальных уравнений. Например, если k зависит от времени. Давайте помечтаем немного и представим, что в какой-то момент времени наука развилась до такого уровня, что требуется все меньше и меньше времени для продления ожидаемой ПЖ на год, то есть k уменьшается со временем.

Пусть, например, k уменьшается по экспоненте с периодом полураспада в n лет. И давайте попробуем ответить на такой вопрос: какой должен быть минимальный m, чтобы человек мог достигнуть longevity escape velocity при таком k (t)?

Чтобы ответить на данный вопрос давайте составим дифференциальное уравнение:

$dx = -dt + \frac{dt}{k_0e^{-bt}}=-dt + \frac{e^{bt}dt}{k_0}(1)$ Надо, пожалуй, пояснить откуда взялось b в экспоненте и чему равняется

Мы определили k (t) = k0*exp (-bt). Так как через n лет значение k (t) должно быть вдвое меньше, то имеем

$\frac{k_0e^{-bt_0}}{k_0e^{-b(t_0+n)}} = 2 => e^{-bt_0 + bt_0 + bn} = 2 => e^{bn} = 2» src=«https://habrastorage.org/getpro/habr/upload_files/e67/61e/489/e6761e4899cc828438ff99ba705f8358.svg» />откуда: <img alt=$ b = \frac{ln (2)}{n}» src=«https://habrastorage.org/getpro/habr/upload_files/23b/ca8/089/23bca8089b668a1c683f1b603da7bd80.svg» />

Интегрируем уравнение и получаем:

$x(t) = -t + \frac{e^{bt}}{bk_0} + C$

Чтобы определить C, воспользуемся начальным условием: x (0)=m:

$x(0) = \frac{1}{bk_0} + C => m = \frac{1}{bk_0} + C => C = m — \frac{1}{bk_0}» src=«https://habrastorage.org/getpro/habr/upload_files/ab1/c06/595/ab1c065956c99b57d75eecef3838b590.svg» />Получаем следующую запись функции дожития: <img alt=$

Давайте взглянем на ее график:

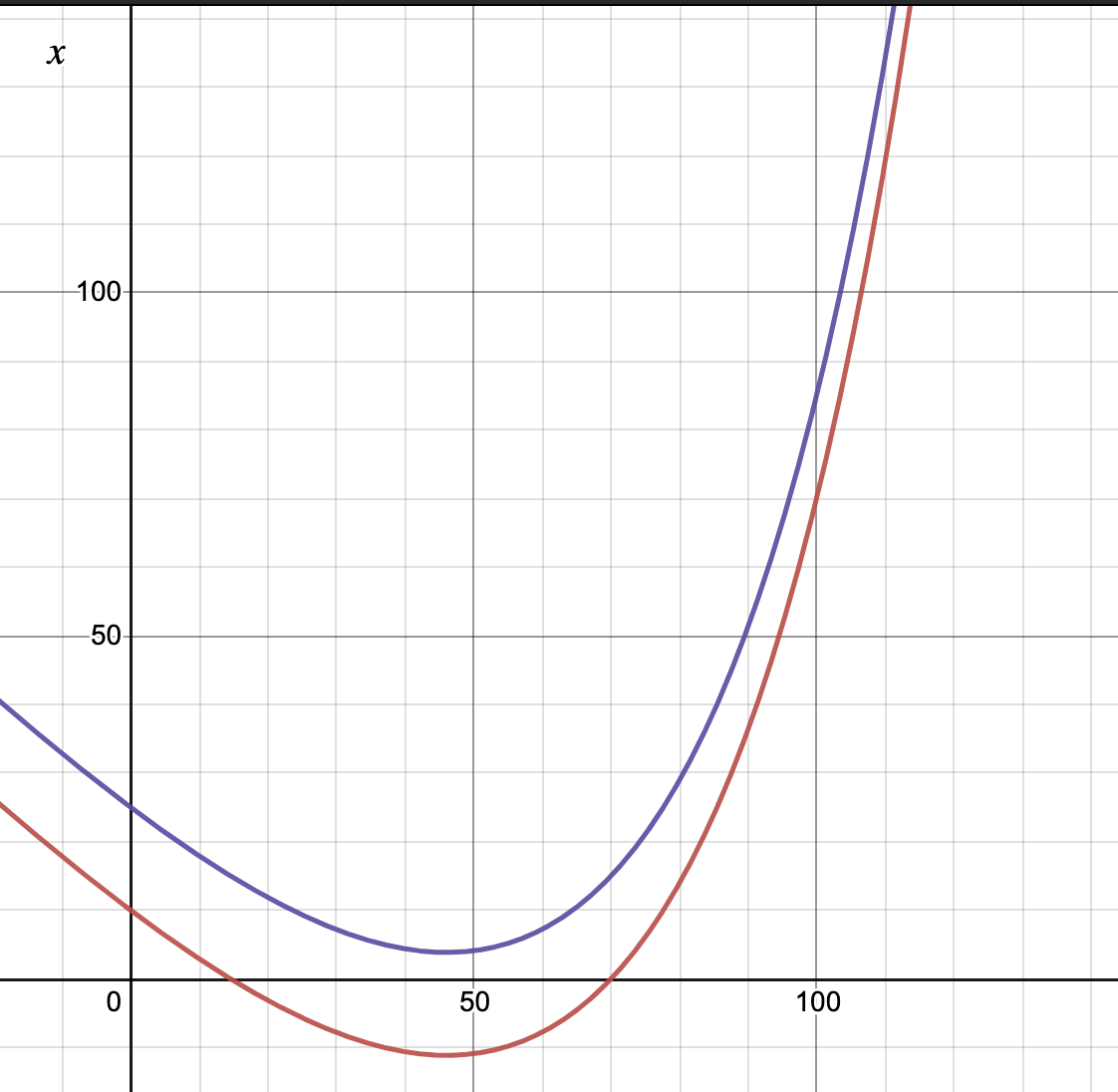Функция x (t) имеет минимум и нам нужно, чтобы этот минимум был выше оси абсцисс (фиолетовая кривая)

Наша функция дожития имеет минимум и все, что нам нужно, это найти значение минимума как функции от m и найти значение m при котором этот минимум больше нуля. Как мы помним еще со школы, для того, чтобы найти минимум функции надо сначала найти ее производную и приравнять к нулю. Причем производную-то мы уже знаем из уравнения (1):

$dx =-dt + \frac{e^{bt}dt}{k_0} => x'(t) = \frac{e^{bt}}{k_0} — 1 => t_{min} = \frac{ln (k_0)}{b}» src=«https://habrastorage.org/getpro/habr/upload_files/bd1/52d/55d/bd152d55de03f1b1adefa44e83ab5972.svg» />Мы точно знаем, что это минимум, потому что вторая производная <img alt=$ положительна на всей области определения, а значит функция выпукла вниз и, следовательно, найденный экстремум является минимумом.

Теперь необходимо найти $x(t_{min})$ :

$x(t_{min}) = -\frac{ln(k_0)}{b} + \frac{e^{b\frac{ln(k_0)}{b}}}{bk_0} + m - \frac{1}{bk_0}=-\frac{ln(k_0)}{b} + \frac{1}{b} + m - \frac{1}{bk_0}$

А отсюда уже выразим ограничение для m:

$m > \frac{ln (k_0)}{b} — \frac{1}{b} + \frac{1}{bk_0} = \frac{k_0ln (k_0)-k_0 +1}{bk_0} = \frac{n (k_0(ln (k_0)-1) +1)}{k_0ln (2)}» src=«https://habrastorage.org/getpro/habr/upload_files/a60/2ca/e92/a602cae9296677856d3f50ec15232592.svg» />При <img alt=$ и k_0=4

необходимо иметь в запасе примерно 9.2 года ожидаемой продолжительности жизни, чтобы достичь longevity escape velocity, то есть быть, например, мужчиной моложе 79 лет. Каждый может прикинуть свои шансы на достижение longevity escape velocity исходя из своего возраста. Но возможно ли в принципе бессмертие? Есть ли какие-то фундаментальные математические (не физические) ограничения? Об этом я расскажу в следующей статье, а пока давайте поговорим о более практических вещах.

Задача 2. Плазмаферез

Конечно, медицинская наука еще очень далека от достижения LEV (а может быть этого и вовсе никогда не случится), однако попытки отсрочить старение ведутся уже сейчас. Одной из самых интересных интервенций, возможно, способной немного продлить молодость и продолжительность жизни является терапевтическое разбавление плазмы. Известные геронтологи супруги Конбои продемонстрировали, что если мышкам заменить половину плазмы на физраствор с альбумином, то у них существенно улучшаются многие показатели жизнедеятельности. Предполагается, что это происходит за счет удаления из организма токсичных продуктов, которые образуются из-за старения организма. Более подробно все описано, например, тут. Более того, некоторые отчаянные биохакеры даже пробуют этот метод на себе и замечают улучшение ряда биомаркеров. Конечно, пройдет еще немало времени прежде чем установят эффективность (или неэффективность) этого метода на людях, но мы тем не менее постараемся ответить на вполне конкретный вопрос:, а сколько раз нам необходимо сдать плазму, чтобы заменить половину, если за один раз забирается v мл?

$x = 1 - \frac{v}{V}$ $x = (1 - \frac{v}{V})^k$

Поскольку нам надо найти такой k при котором обновится половина плазмы, то приравняем правую часть уравнения выше к ½, прологарифмируем обе части равенства и воспользуемся свойствами логарифма, чтобы получить формулу для k:

$\frac{1}{2} = (1 - \frac{v}{V})^k => -ln (2) = kln (1-\frac{v}{V}) => k = \frac{-ln (2)}{ln (1 — \frac{v}{V})}» src=«https://habrastorage.org/getpro/habr/upload_files/106/f6f/e33/106f6fe3379b97d2644766ec593c8fd9.svg» />Удельный объем плазмы взрослого мужчины составляет, в среднем, 46.7 мл/кг. Возьмем к примеру мужчину массой 80 кг и v=450 мл (стандартный объем плазмы при донорстве): <img alt=$

То есть взрослому сорокалетнему мужчине массой 80 кг необходимо за короткий срок 6 раз пожертвовать плазму, чтобы ее обновить чуть более чем наполовину.

Пусть X (t) — доля старой плазмы в момент времени t. Пусть скорость вытекания плазмы равна r мл/мин. Чему же будет равна концентрация старой плазмы в момент времени t + dt? А концентрация равна:

$X(t + dt) = \frac{X(t)V - X(t)rdt}{V}$

Давайте разберем каждое составляющее этого равенства:

X (t)V: концентрация старой плазмы помноженная на общий объем — очевидно это объем старой плазмы во всем организме в момент t

X (t)rdt: это объем старой плазмы, который вытечет за время dt (rdt — это скорость истечения, помноженная на время, что соответствует объему, а X (t) — это доля старой плазмы в этом объеме).

Затем мы делим получившийся объем старой плазмы на общий объем (который остается неизменным, потому что физраствор втекает с той же скоростью) и получим концентрацию. А теперь узнаем чему равно изменение концентрации (разница между концентрацией в моменты времени t+dt и t):

$X(t + dt) = X(t) - \frac{X(t)}{V}rdt => X (t + dt) — X (t) = — \frac{X (t)}{V}rdt => dX = -\frac{X (t)}{V}rdt» src=«https://habrastorage.org/getpro/habr/upload_files/e08/f0b/273/e08f0b27308748325ba95b8be3e93507.svg» />Разделяем переменные и решаем это дифференциальное уравнение: <img alt=$ ln|X (t)| = -\frac{rt}{V}+C_1» src=«https://habrastorage.org/getpro/habr/upload_files/ca3/f71/a95/ca3f71a9549601fdf87fad0d64256245.svg» />

Отсюда:

$X(t) = Ce^{-\frac{rt}{V}}$

Мы знаем, что вначале концентрация старой плазмы равнялась 1:
X (0) = 1 => C = 1

Поэтому $X(t) = e^{\frac{-rt}{V}}$ , а теперь найдем время, за которое обновится половина плазмы:

$\frac{1}{2} = e^{\frac{-rt_{1/2}}{V}} => -ln (2) = -\frac{rt_{½}}{V} => t_{½} = \frac{Vln (2)}{r}» src=«https://habrastorage.org/getpro/habr/upload_files/714/ab6/82f/714ab682fd36fd7528ad1f1cbecf78d1.svg» />На практике это означает примерно 259 минут (4 с лишним часа!), если руководствоваться средней скоростью 10 мл/мин (обычно забирают 450 мл плазмы и уходит на это примерно 45 минут): <img alt=$

Конечно, это время абсолютно неприемлемо, однако процедуру можно существенно ускорить. Например, в этой статье описан метод, который позволяет изымать плазму со скоростью 24 мл/мин, что позволяет заменить половину плазмы за 108 минут. Весьма неплохо! Однако неизвестно выдержит ли организм замену половины плазмы за один раз :) Но это уже выходит за рамки математики, оставим этот вопрос врачам. Тем более, что различные клинические исследования по влиянию плазмафереза на старение людей уже начались.