Диаграммы Вороного для аэропортов и столиц
сегодня в 02:36
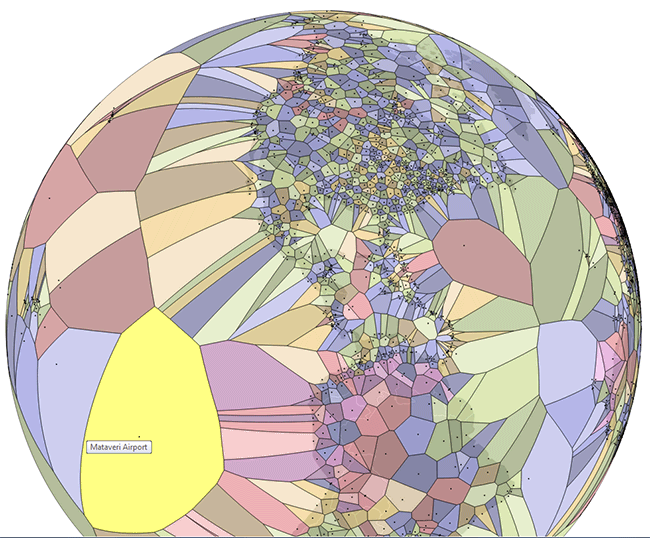
Диаграмма Вороного конечного множества точек S на плоскости представляет такое разбиение плоскости, при котором каждая область этого разбиения образует множество точек, более близких к одному из элементов множества S, чем к любому другому элементу множества.
Эксперт по визуализации данных и информатике Джейсон Дэвис (Jason Davies) на своём сайте выложил несколько любопытных экспериментов, в том числе со сферическими диаграммами Вороного.
Диаграмма вверху показывает, какую территорию земного шара покрывает каждый аэропорт. Видно, что в некоторых точках планеты нет ни одного аэропорта на тысячи километров.
Интересно также посмотреть на диаграмму Вороного для мировых столиц (внизу). Она показывает, как могла бы выглядеть карта мира, если разделить территории по «справедливости», то есть по максимальной близости к столице. В этом случае, например, большую часть территории США разделили бы между собой Канада и Мексика.
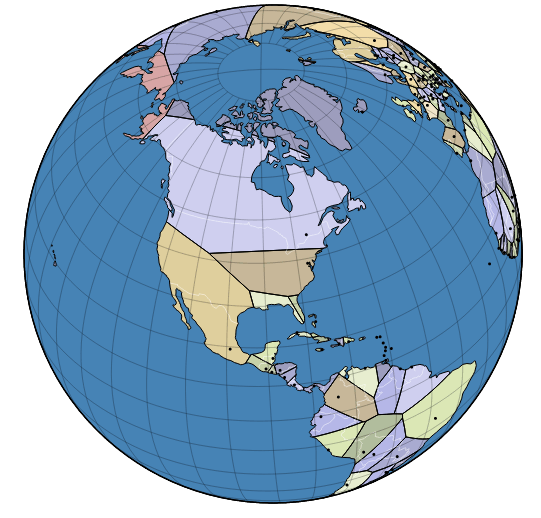
Москве тоже не повезло: она находится далеко от своих провинций. Так что Сибирь поделят между собой Монголия и Казахстан.

Территория Северной Кореи выросла бы в десятки раз за счёт Забайкалья, а Япония реализовала бы давнюю мечту вернуть Курильские острова (а заодно Камчатку, Чукотку и кусочек Аляски).
