CRC — это просто (деление столбиком)
Введение
Целостность — это важное свойство системы.
Будет плохо, если пользовательские данные будут искажены, а мы и глазом не моргнем.
Существуют различные способы достижения этого. Как например, коды коррекции или обнаружения ошибок.
Собственно задача следующая: нам поступают пакеты данных и в процессе передачи данные могут быть искажены, поэтому принимающая сторона должна уметь обнаруживать подобные ситуации.
Одним из таких механизмов является CRC (Cyclic Redundancy Check) — циклический избыточный код. Именно его я решил использовать для проверки целостности в приложении. Его реализаций в интернете полно — Ctrl + C, Ctrl + V не хочу. Но я не я, если бы не сделал свой велосипед разобрался как этот алгоритм работает.
Обзор алгоритма
Грубо говоря, CRC — это просто остаток от деления. Но до этого мы еще дойдем.
Деление чисел с остатком
Что мы хотим — обнаружение изменения даже одного байта сообщения. Т.е. все биты данных должны учитываться. Но неплохо было бы иметь и «лавинность» как у криптографических хэш-функций. На ум приходит деление, а точнее остаток от деления.
Поделим на
и получим в остатке
.

Деление 645372 на 43621
Поменяем только 1 цифру в делимом и попробуем снова: .

Деление 644372 на 43621
Результат изменился — и
не равны.
Что если представить поток байт, для которого нужно подсчитать чек-сумму, в виде очень большого числа? Тогда нам остается только найти остаток от деления этого большого числа на делитель.
Уже неплохо. Но как этот делитель найти? Тут надо вспомнить важное свойство остатка — он всегда меньше делителя. Прекрасно! Тогда возьмем такой делитель, чтобы остаток укладывался в определенное число байт.
К примеру, если чек-сумма должна быть 4 байтной, то и максимальное значение делителя должно быть меньше .
Основу заложили — представляем байты в виде большого числа и находим его остаток от деления на число меньше .
Посмотрим, как реализуется деление с остатком в двоичном виде:

Деление двоичных чисел
Деление многочлена с остатком
Но работа в CRC ведется с полиномами, а не числами.
Тут мы подходим к другой важной концепции: остаток от деления многочлена.
Получить остаток от деления можно не только от числа, но и от многочлена. Он определяется так же как и для обычных чисел. Разница только в том, что результатом будет не число, а многочлен.
Например, поделим многочлен на
, тогда в результате получим:
Частное:
Остаток:

Деление многочлена
Но при чем тут многочлены?
Дело в том, что многочлен можно закодировать в последовательность чисел, где каждое отражает коэффициент при соответствующей степени.
Число | |||||||
|---|---|---|---|---|---|---|---|
1 | 8 | ||||||
1 | 1 | ||||||
1 | |||||||
8 | -1 |
Многочлены над конечным полем GF (2)
Можно подметить, что двоичные числа — это закодированные многочлены. Но есть один момент, который нужно учитывать — перенос коэффициентов.
Например, возьмем и
. Их двоичное представление:
и
соответственно. Если мы их перемножим то получим:
Вот тут мы можем заметить разницу между операциями над двоичными числами и операциями с многочленами — работа с коэффициентами. Когда мы перемножали многочлены, то получили и
, но коэффициент
закодировать в двоичном представлении не можем. То если, просто так, работать с двоичными числами как многочленами — не можем.
Здесь на арену приходит »полиномиальная арифметика по модулю 2».
Вкратце, она говорит, что
полиномиальная арифметика — Все коэффициенты при каждой степени независимы друг от друга
по модулю 2 — Результирующий коэффициент — это остаток от деления полученной суммы коэффициентов на 2 (поле
— вики)
Попробуем умножить 2 многочлена в этой арифметике — и
:

Умножение 2 многочленов в поле GF (2)
К получившейся сумме добавим :

Сложение с другим многочленом
Складываем все вместе
Но зачем вся эта информация?
Дело в том, что CRC работает в терминах многочленов над конечным полем GF (2) — полиномиальная арифметика по модулю 2. В частности, операции над числами в битовом представлении и есть это представление операций над такими многочленами (биты представляют коэффициенты).
Подытожим:
Работаем с многочленами в конечном поле по модулю 2 (
);
На вход подается многочлен — байты для вычисления чек-суммы;
Делитель — другой многочлен/полином (его называют порождающим многочленом);
Задача CRC — найти остаток от деления переданного многочлена на порождающий.
Также важно уточнить, что порождающий многочлен всегда будет иметь в начале (старшим битом) 1.
Например, 8-битный полином на самом деле будет равен
или в CRC32, который порождает 4 байтную (32 бита) чек-сумму, полином, на самом деле, 33 битный. Чаще всего он опускается, т.к. алгоритм построен так, чтобы можно было не писать его явно.
И главное, что надо заметить: XOR операции над двоичными числами отражают соответствующие операции деления многочленов над конечным полем .
Вот пруфы:

Деление многочлена в поле GF (2)
А теперь, это же деление, но используя представление в виде двоичных чисел:

Деление этого многочлена, но в двоичном представлении
Результат мы получаем один и тот же — зачем платить больше?
Дальше будем говорить о делителе как о числе, а не полиноме.
Реализация в лоб
Реализация у нас уже на руках. Осталось только несколько моментов:
Добавим регистр — переменную, в которой будем хранить промежуточный результат после каждого шага вычитания. Его размер должен быть таким же как и у результата.
Сообщение нужно дополнять в конце нулевыми байтами, чтобы регистр смог правильно обработать сообщение. Дополнять нужно столько-же, сколько занимает регистр (в битах).
Далее будем вычислять CRC для:
Полинома:
Сообщения:
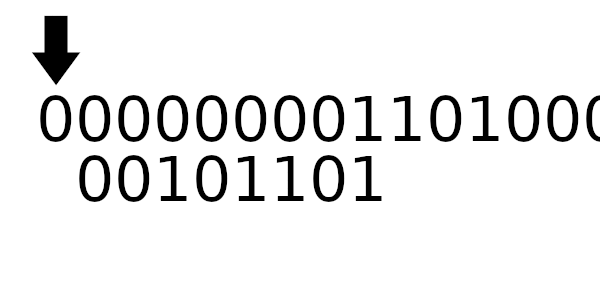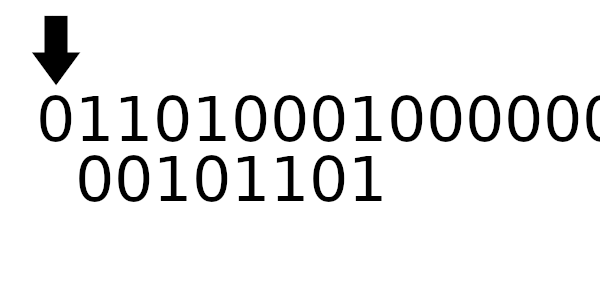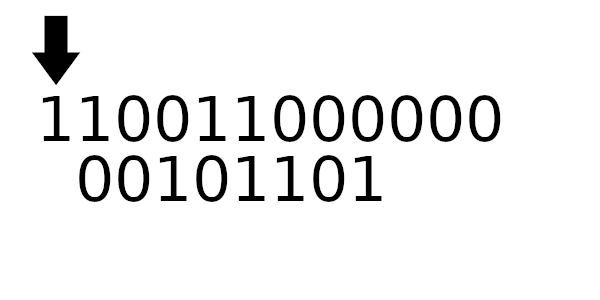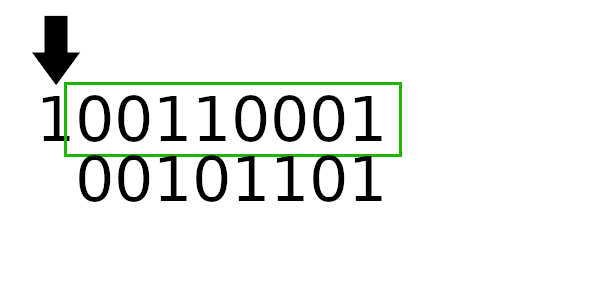
Визуализация работы побитовой реализации
Заметьте дополняющие биты вначале и в конце
uint InitialSimpleRegister = 0xFFFFFFFF;
uint Polynomial = 0x04C11DB7;
uint ComputePerBit(byte[] payload)
{
var register = InitialSimpleRegister;
foreach (var bit in IterateBits())
{
var bitSet = ( register & 0x80000000 ) != 0;
register <<= 1;
register |= bit;
if (bitSet)
{
register ^= Polynomial;
}
}
// Обрабатываем нулевые биты сообщения (дополненные)
for (var i = 0; i < 32; i++)
{
var bitSet = ( register & 0x80000000 ) != 0;
register <<= 1;
// Дальше идут только 0
// register |= bitSet;
if (bitSet)
{
register ^= Polynomial;
}
}
return register;
IEnumerable IterateBits()
{
foreach (var b in payload)
{
for (byte byteMask = 0b10000000; byteMask != 0; byteMask >>= 1)
{
yield return ( b & byteMask ) == 0
? 0u
: 1u;
}
}
}
}
Оптимизируем работу с байтами (табличная реализация)
Предыдущая реализация режет глаз. Она не оптимальна, как минимум, потому что компьютер работает с байтами, а не потоком бит. Хотелось бы, чтобы работа велась с минимальным куском (byte) данных — байтом.
Есть один момент, который стоит заметить, — зависимость операций: каждая операция зависит от текущего бита и предыдущих операций — в будущее мы не смотрим.
Для примера рассчитаем табличные значения для и
(пригодятся дальше), а полином возьмем из предыдущего примера:
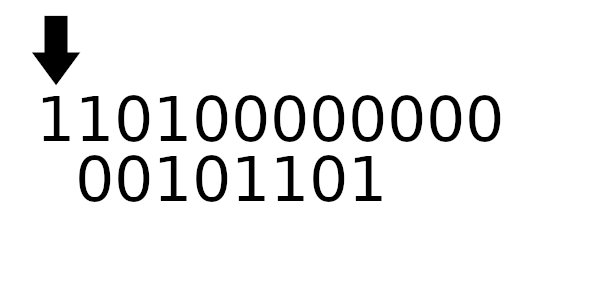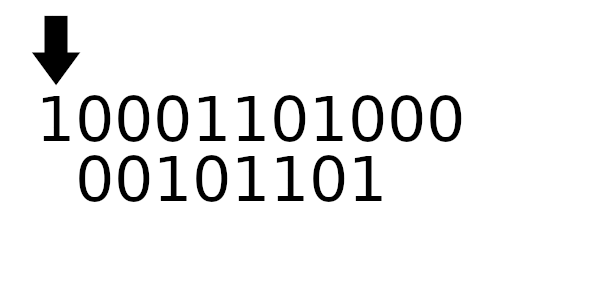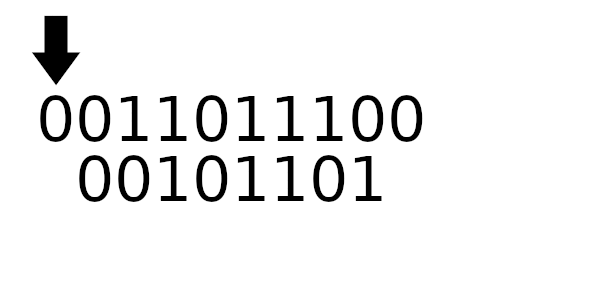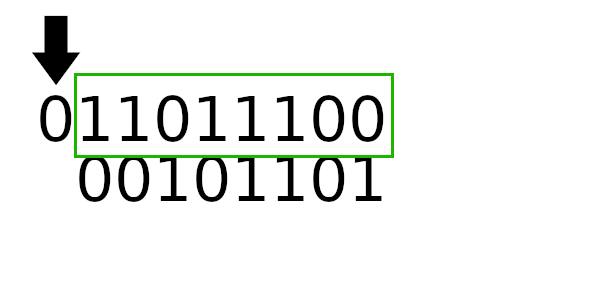
Табличное значение для 1101
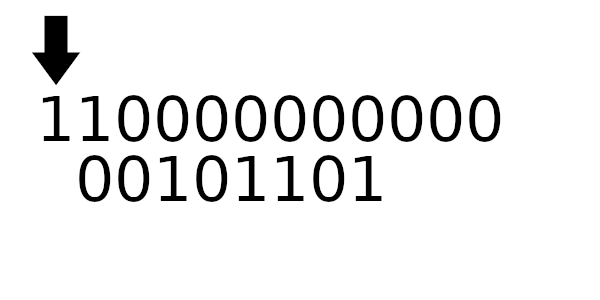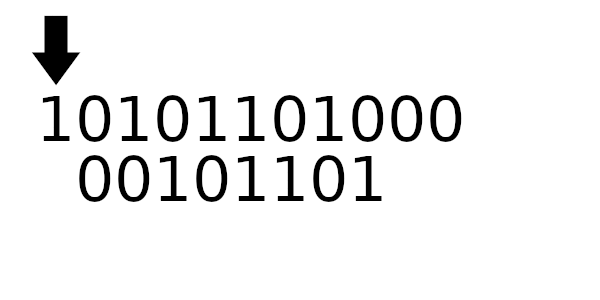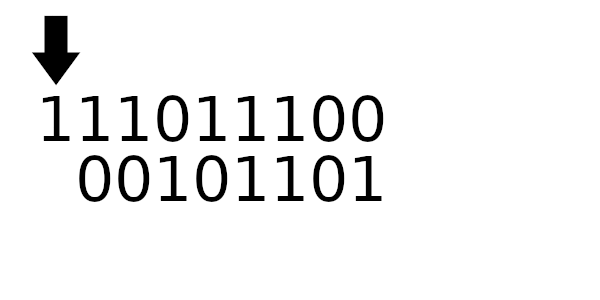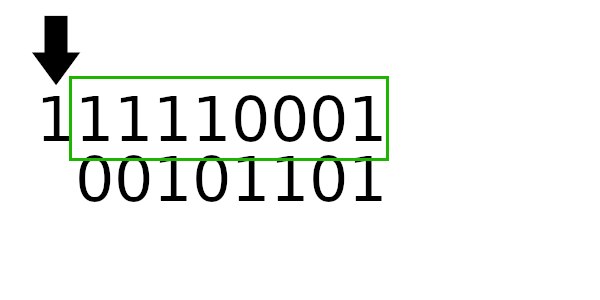
Табличное значение для 1100
А к чему будет это значение применяться? К новому регистру — регистр смещается влево и к нему добавляется байт сообщения. Теперь рассчитаем значение полинома используя этот алгоритм:
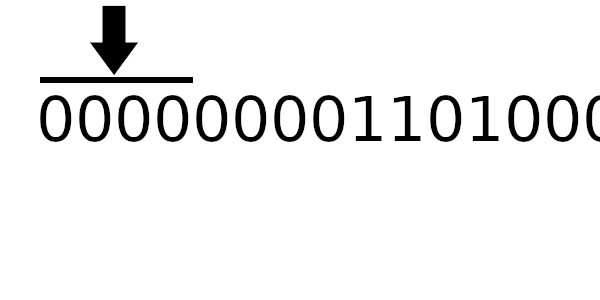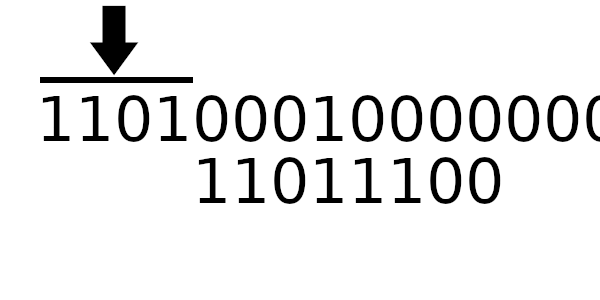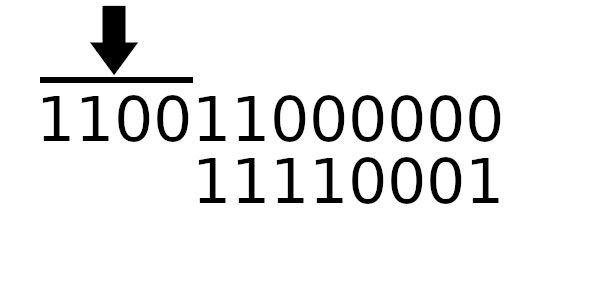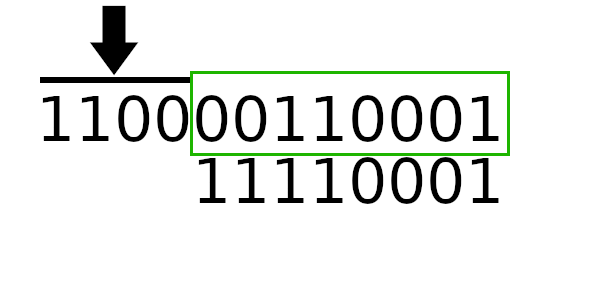
Простой табличный алгоритм
Компьютер всегда работает с байтами — отдельных битов быть не может. Давайте вычислим значения, которые нужно применять, в зависимости от старшего байта!
В этом и заключается оптимизация — создание подобной таблицы.
uint[] ComputeCrcTable()
{
var table = new uint[256];
for (int i = 0; i < 256; i++)
{
var crc = ( uint )( i << 24 );
for (int bit = 0; bit < 8; bit++)
{
var bitSet = ( crc & 0x80000000 ) != 0;
crc <<= 1;
if (bitSet)
{
crc ^= Polynomial;
}
}
table[i] = crc;
}
return table;
}
uint ComputeTableSimple(byte[] payload)
{
var table = ComputeCrcTable();
var register = InitialSimpleRegister;
foreach (var b in payload)
{
register = ( ( register << 8 ) | b ) ^ table[register >> 24];
}
for (int i = 0; i < 4; i++)
{
register = ( register << 8 ) ^ table[register >> 24];
}
return register;
}
Дальнейшие оптимизации
Заметили дополнительный цикл, который идет после обработки самого сообщения? Это дополняющие биты, о которых было сказано ранее. Вроде 4 байта, но не всегда удобно следить за таким (да и не совсем красиво).
Можно, конечно, заставить самого пользователя добавлять нулевые биты в конце, но тогда может нарушиться логика, если внезапно забудешь это сделать.
На самом деле, эту проблему уже решили. Причем, на мой взгляд, кардинальным способом — изменили сам алгоритм (взгляд на него).
Чтобы понять, что имеется ввиду, обратим внимание на следующие факты:
Конечные нулевые байты нужны только для того, чтобы были корректно обработаны все байты исходного сообщения. Причем сами нули ни на что не влияют (
x XOR 0 = x). Т.е. по факту, можно их не добавлять — главное провести все байты сообщения через алгоритм.Первые 4 цикла — это просто загрузка первых 4 байт сообщения. Причем независимо от того, что в регистре было изначально, этот этап можно опустить/сократить и сразу начать загружать байты сообщения.
Почему первые 4 цикла можно опустить
В зависимости от значения регистра может быть 2 случая:
Изначально был 0
Все просто — первые 4 цикла загрузят первые 4 байта сообщения и никаким образом их не изменят. Изменений не будет, так как табличное значение для 0 — это 0, а x XOR 0 = x (дает исходное значение).
Это можно заметить, если приглядеться к визуализациям выше.
Изначально был НЕ 0
Этот случай не отличается от того, что если бы мы выполнили XOR между первыми 4 байтами сообщения и другим начальным значением регистра. Только это новое значение регистра не случайное, а вычисляется из изначального значения регистра старого алгоритма (об этом дальше).
Как работает получение индекса для табличного значения
В старом алгоритме, после сдвига регистра в конец дописывалось само сообщение (его первые байты). А после, по мере работы алгоритма, к нему применялись операции из таблицы.
Т.е. происходило следующее: message_byte XOR op1 XOR op2 XOR op3:
message_byte— байт сообщения, который дописали в конецop*— применяли соответствующие табличные операции (* — номер операции)
Заметим 2 факта:
XOR — ассоциативен. Это значит, что
message_byte XOR op1 XOR op2 XOR op3дает тот же самый результат, что иop1 XOR op2 XOR op3 XOR message_bytex XOR 0 = x— XOR с 0, даст исходный результат.
Суммируя выше сказанное, можно переписать message_byte XOR op1 XOR op2 XOR op3 в 0 XOR op1 XOR op2 XOR op3 XOR message_byte.
В итоге, можно сделать такую корректировку алгоритма:
После сдвига регистра можно не писать добавлять байты сообщения, а оставить 0 —
0По мере работы алгоритма, в этой части соберется накопленное значение всех операций —
0 XOR op1 XOR op2 XOR op3Когда нужно сдвинуть старший байт, то берем этот байт из сообщения только в этот момент —
0 XOR op1 XOR op2 XOR op3 XOR message_byte
Результат будет один и тот же
После небольшой модификации, алгоритм становится следующим:
Инициализируем регистр
register(уже новым значением)Для каждого байта
bиз сообщения:Берем старший байт из регистра
top_byteСдвигаем регистр на байт влево
Вычисляем индекс для таблицы:
b XOR top_byteПолучаем значение из таблицы по полученному индексу
XOR’им регистр с полученным значением из таблицы
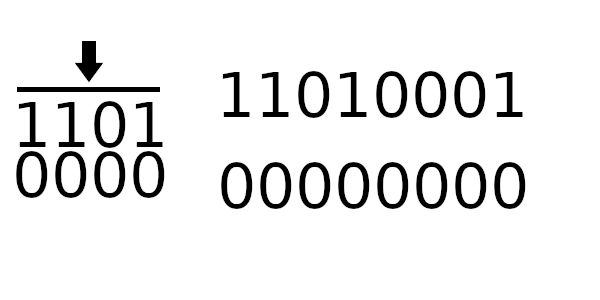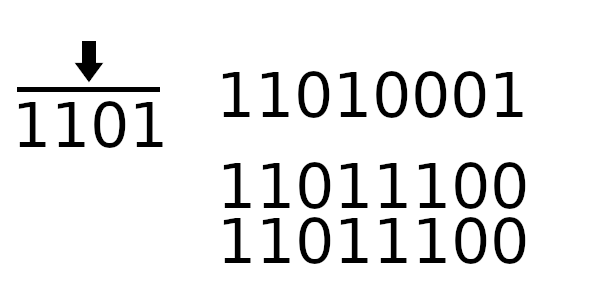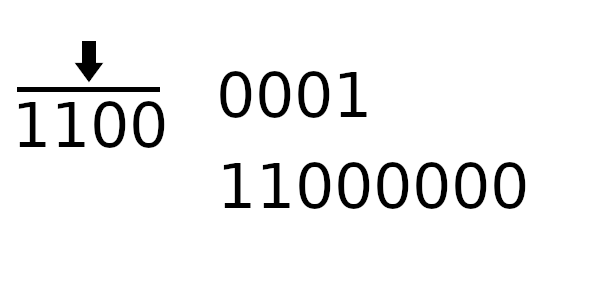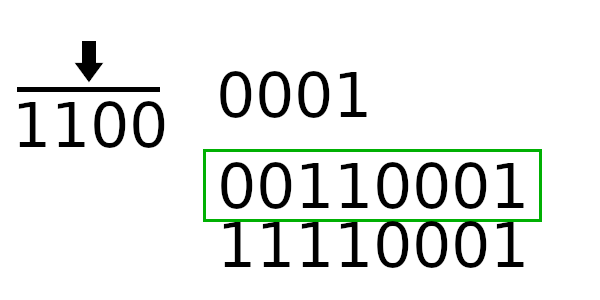
Оптимизированный табличный алгоритм
Единственное, что пока непонятно — как рассчитывать новое начальное значение регистра. Чтобы вычислить новое значение регистра, нужно пропустить старое через цикл 4 раза (только начальное значение, без байтов сообщения).
uint ComputeNewInitialValue()
{
var register = InitialSimpleRegister;
for (var i = 0; i < 32; i++)
{
var bitSet = ( register & 0x80000000 ) != 0;
register <<= 1;
if (bitSet)
{
register ^= Polynomial;
}
}
return register;
}
Пример с ненулевым начальным регистром
Для примера возьмем то же самое число, но начальное значение регистра на этот раз будет 01100000.
Нам также потребуются табличные значения:
Ключ | Значение |
|---|---|
0110 | 11101110 |
1001 | 01101000 |
1100 | 11110001 |
1110 | 10101011 |
Рассчитаем CRC для обычного табличного алгоритма:

Простой табличный алгоритм с ненулевым начальным регистром
В результате мы получили:
Теперь попробуем новый табличный алгоритм. Для начала вычислим новое значение регистра:
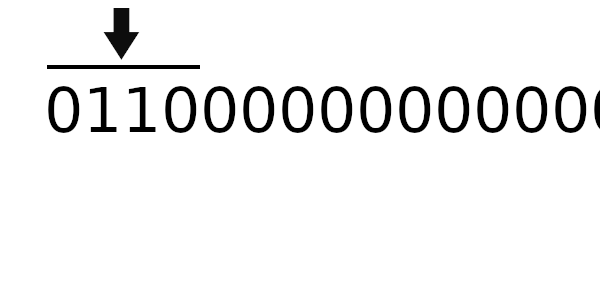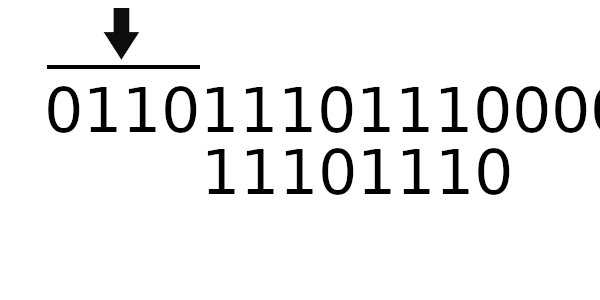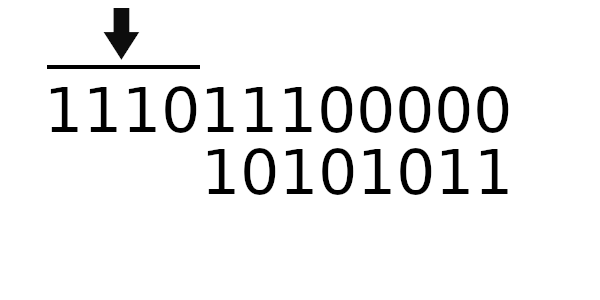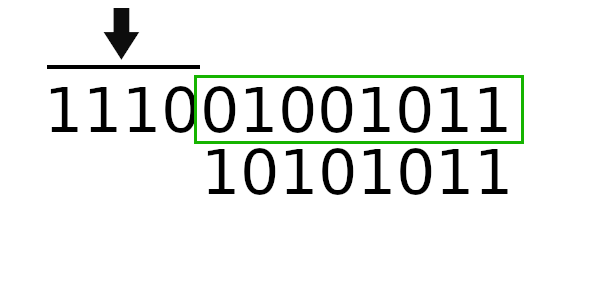
Расчет начального значения регистра
И теперь сам CRC:

Оптимизированный табличный алгоритм с ненулевым начальным регистром
Новый табличный алгоритм дал 01110001 — то же самое значение.
Собственно сам код оптимизированного табличного алгоритма:
uint InitialOptimizedRegister = 0xC704DD7B;
uint ComputeTableOptimized(byte[] payload)
{
var register = InitialOptimizedRegister;
foreach (var b in payload)
{
register = ( register << 8 ) ^ Table[( register >> 24 ) ^ b];
}
return register;
}
uint ComputeTableOptimized(byte[] payload)
{
var register = InitialOptimizedRegister;
foreach (var b in payload)
{
register = ( register << 8 ) ^ Table[( register >> 24 ) ^ b];
}
return register;
}
Параметризация
На текущий момент, мы увидели 3 места, которые могут быть настроены:
Размер полинома
Значение полинома
Исходное значение регистра.
Но на самом деле их больше. Можно добавить еще 2 параметра:
XOR конечного результата с каким-то числом — перед возвращением результата он XOR’ится с каким-то числом
Порядок байтов — можно указать, что при работе все биты должны быть отзеркалены (UART отправляет биты в обратном порядке)
Росс Уильямс выделяет такую параметризацию:
Width — Степень полинома, число битов в регистре
Poly — Значение полинома
Init — Стартовое значение (указывается именно для табличного варианта)
RefIn (Reflect In) — Изменить порядок бит перед началом обработки
RefOut (Reflect Out) — Изменить порядок бит перед передачей на XorOut этап
XorOut — Значение с которым нужно XOR’ить результирующее значение перед возвращением
Также есть 2 дополнительных поля. Лично я отношу их больше к метаданным:
Name — Название алгоритма (этого сборника параметров)
Check — Результирующее значение при обработке строки »123456789» (в ASCII кодировке)
Некоторые варианты реализации представлены в таблице ниже
Name | Width | Poly | Init | RefIn | RefOut | XorOut | Check |
|---|---|---|---|---|---|---|---|
CRC-5/ITU | 5 | 0×15 | 0×0 | true | true | 0×0 | 0×7 |
CRC-8 | 8 | 0×7 | 0×0 | false | false | 0×0 | 0xF4 |
CRC-16/USB | 16 | 0×8005 | 0xFFFF | true | true | 0xFFFF | 0xB4C8 |
CRC-32/MPEG-2 | 32 | 0×04C11DB7 | 0xFFFFFFFF | false | false | 0×0 | 0×376E6E7 |
Заключение
Ну вот мы и прошли этот эволюционный путь от обработки потоков битов, до оптимизированного табличного алгоритма.
Но есть еще несколько тем, которые не были раскрыты
Выбор полинома
От выбора полинома зависит вероятность обнаружения ошибки.
Филлип Купман провел исследование влияния различных полиномов на вероятность нахождения ошибок за нас (сайт). Он исследовал зависимость расстояния Хэмминга ошибок от полинома (и его длины соответственно).
Исследования выявили оптимальные полиномы для расстояний Хэмминга от 2 до 6 (т.е. может заметить от 1 до 5 ошибок). Ниже представлена часть таблицы с лучшими найденными полиномами:
Расстояние хэмминга / Размер полинома | 8 | 16 | 32 |
|---|---|---|---|
2 | 0xE7 | 0×8D95 | 0xAD0424F3 |
3 | 0xE7 | 0×8D95 | 0xAD0424F3 |
4 | 0×83 | 0xD175 | 0xC9D204F5 |
5 | 0xEB | 0xAC9A | 0xD419CC15 |
6 | 0×9B | 0×9EB2 | 0×9960034C |
Аппаратная поддержка
Вычисление CRC на столько популярна, что специальные операции были добавлены машинные инструкции:
