Число, лежащее в основе современной музыки15.10.2019 19:48

Почему двенадцать?

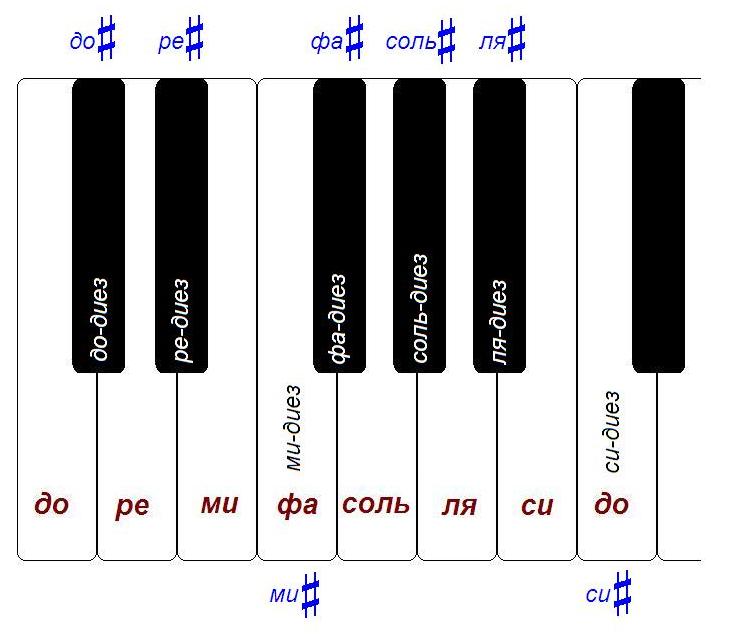
Если вы посмотрите на клавиатуру, то увидите, что в каждой октаве содержится 12 полутонов.
В случае фортепиано это всего лишь значит, что между, например, «до» первой октавы и «до» второй октавы расположено 11 клавиш. Вместе с одним из «до» (например, до второй октавы) мы получим 12 клавиш: до#, ре, ре#, ми, фа, фа#, соль, соль#, ля, ля#, си, до.

Но почему 12?

Может быть это просто случайность? Вот нравилось нашим предкам число 12, у них везде 12: 12 месяцев, 12 знаков зодиака, 12 колен Израилевых, 12 апостолов, … и здесь решили, пусть будет 12, и так и повелось. Или все же здесь есть объективный закон, и это число не случайно?

В этой статье я докажу, что это не случайность, и что 12 является единственно возможным вариантом в современном музыкальном строе, что в свою очередь является следствием свойств одного числа. Я бы даже сказал, что это число лежит в основе современной музыки.

Постановка задачи

Сначала давайте попробуем формализовать задачу.

У нас есть опорная частота $\omega_0$ . Будем называть ее тоникой. У нас также есть октава с частотой $2\omega_0$ . Теперь мы должны понять, какие могут быть варианты промежуточных частот от $\omega_0$ до $2\omega_0$ , такие, чтобы мелодия, построенная на этих нотах, звучала бы для нашего слуха гармонично?

Боюсь, что эта формулировка, хотя и отражает суть вопроса, все же, с математической точки зрения, является довольно туманной, и на такой вопрос не может быть однозначного ответа, хотя бы потому, что человеческий слух имеет довольно ограниченную разрешающую способность по частоте. И это подтверждается тем, что в разное время использовались разные строи, например, пифагоров, чистый, хорошо темперированный, равномерно темперированный строи. И все они звучали и звучат, как минимум для определенных произведений, вполне приемлемо.

Что такое гармония?

Мы должны наложить некоторые дополнительные условия. Но прежде мы должны ответить на один важный вопрос: что мы воспринимаем как гармоничное звучание?

Давайте рассмотрим два звука — с частотами $\omega_1$ и $\omega_2$ .

Возьмем отношение этих частот. Это отношение можно представить в виде произведения чисел $a_1^{k_1}\cdot a_2^{k_2}\cdot...\cdot a_l^{k_l}$ , где $a_1, a_2,..., a_l$ — простые числа, а $k_1, k_2,..., k_l$ — целые числа, например, это отношение может равняться $2^{-3}\cdot3\cdot5$ . И чем эти простые числа () меньше, тем гармоничнее для нашего уха будет звучать этот интервал (я нашел это утверждение тут (см. второй абзац))

Так, например, самым гармоничным звучанием в соответствии с этим утверждением будет являться октава (изменение частоты в 2 раза). А следующими по гармоничности интервалами будут квинта (изменение частоты в $3/2$ раза) и кварта (изменение частоты в $4/3$ раза).

Но не так все просто с этим утверждением. Так, например, не очень понятно, как влияет степень. Например, что гармоничнее умножение на $3^2$ или на 7? Я не знаю, изучен этот вопрос или нет, и можно ли в принципе дать на него ответ. Также восприятие гармоничности — вещь довольно субъективная. Так, современная музыка полна звучаний, которые 100 — 200 лет были бы восприняты не иначе как жуткая какофония.

Условие первое. Тоника, кварта, квинта, октава

Эта неопределенность не является проблемой для нашего маленького исследования. Дело в том, что единственный вывод, который я хочу сделать из этого утверждения заключается в том, что в нашем строе в любом случае должны быть как минимум «самые гармоничные» интервалы, а именно, октава, кварта и квинта. То есть наряду с тоникой с частотой $\omega_0$ и октавой с частотой $2\omega_0$ у нас также должны быть квинта и кварта, с частотами соответственно ${3\over 2}\omega_0$ , ${4\over 3}\omega_0$ или что-то очень близкое, что мы не смогли бы отличить от чистой квинты и кварты.

И это наше первое требование.

Условие второе. Инвариантность

Вторым нашим требование будет инвариантность. И это важное требование современной музыки. Заключается это требование в том, что все гармонии в любых тональностях должны звучать одинаково. Если мы говорим про современный строй, который применяется при настройке фортепиано, то это значит, что квинта, состоящая из семи полутонов, должна звучать одинаково, независимо от того, от какого звука она построена. То есть соотношение частот между до и соль должно быть таким же как и для до# — соль#, ре — ля, ре# — ля#, … и равняться $3/2$ . И эта инвариантность должна относится, конечно, не только к квинте, но и к любым интервалам. Важным преимуществом этого строя является возможность транспонирования пьесы на любой интервал. В этом и заключается суть равномерной темперации.

Нужно сказать, что это требование инвариантности не является таким очевидным, и данный подход был применен относительно недавно, лишь в 18 веке. Строи, применявшиеся до этого, (например, пифагоров и чистый) не обладали таким свойством. Вот послушайте, например, Sonata for Microtonal Piano (Ben Johnston), написанную в чистом строе (prime limit = 5). Такое ощущение, что фортепиано не настроено. Все богатство современных гармоний, основано именно на этой инвариантности. Например, «Хорошо темперированный клавир» Баха появился именно благодаря новому подходу в настройке клавишных. Именно вот эта инвариантность дала возможность Баху создавать гармонические последовательности, которые просто были невозможны раньше.

Итак, теперь мы имеем все необходимые для расчета данные.

Расчет

Давайте построим звукоряд от тоники до октавы, который бы удовлетворял обоим требованиям.
Предположим, что в этом случае мы получим $N$ звуков (включая октаву). Это $N$ и является искомым числом. Мы хотим показать, что $N$ при наших условиях должно равняться 12.

Следствием второго требования является то, что интервал между частотами соседних звуков должен быть одинаковым и должен быть равен $2^{1\over N}$ .

Теперь первое требование говорит о том, что в нашем ряду должны быть два звука, соответствующие (с хорошим приближением) частотам ${3\over 2}\omega_0$ и ${4\over3}\omega_0$ . Это квинта и кварта. Предположим, что кварта это $n_1$ -ый звук в нашем ряду, а квинта — $n_2$ -ой. Обозначим $n = n_2 - n_1$ .

Нетрудно видеть, что изменение частоты между квартой и квинтой (отношение частот) равно $9/8$ .

Но, в соответствии с нашим вторым условием, это также должно быть равно $2^{n\over N}$ .

Итак, мы получили формулу:

$2^{n\over N} \approx 9/8$

После несложных преобразований получим основную формулу:

$n \approx N(2\log_2 {3} - 3) = N\cdot 0,170$

Легко увидеть, что решением (конечно, приблизительным) является $N = 6i $ , где $i$ — любое натурально число.

Давайте рассмотрим случай $i = 1$ . В этом случае $N = 6$ , $n = 1$ . То есть, это вариант современного строя, только без полутонов, только с тонами (до, ре, ми, фа#, соль#, ля#, до). Но, как вы видите, в этом случае кварта (фа) и квинта (соль) в этот звукоряд не попали.

То есть единственным вариантом для нас может быть

$N = 12 i $ , где $i$ — любое натурально число. Случай $i =1$ как раз и соответствует нашему современному строю, который называется равномерно темперированный строй.

Но почему не 24, 36, 48…? Причина проста — наш слух уже не различает этой градуированности. Поэтому остается только одно число: 12.

Заключение. Число, лежащее в основе

Удивительно, но получается, что числом, лежащим в основе современного музыкального строя и всей современной музыки, является $\log_2{3}$ , а именно то, что с хорошей точностью (0,1%) выполняется следующее равенство:

$\log_2 {3} \approx 19/12$