Численные методы решения уравнений эллиптического типа03.08.2018 10:03

Введение


Наиболее распространённым уравнением эллиптического типа является уравнение Пуассона.
К решению этого уравнения сводятся многие задачи математической физики, например задачи о стационарном распределении температуры в твердом теле, задачи диффузии, задачи о распределении электростатического поля в непроводящей среде при наличии электрических зарядов и многие другие.

Для решения эллиптических уравнений в случае нескольких измерений используют численные методы, позволяющие преобразовать дифференциальные уравнения или их системы в системы алгебраических уравнений. Точность решения опреде­ляется шагом координатной сетки, количеством итераций и разрядной сеткой компьютера [1]

Цель публикации получить решение уравнения Пуассона для граничных условий Дирихле и Неймана, исследовать сходимость релаксационного метода решения на примерах.
Уравнение Пуассона относится к уравнениям эллиптического типа и в одномерном случае имеет вид [1]:

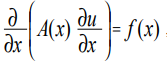3dgua8aaenup1nhwe6d3mgwc0og.png (1)

где x — координата; u (x) — искомая функция; A (x), f (x) — некоторые непрерывные функции координаты.

Решим одномерное уравнение Пуассона для случая А = 1, которое при этом принимает вид:

i9zoyeml4g56q9culr1maeltexw.png (2)

Зададим на отрезке [xmin, xmax] равномерную координатную сетку с шагом ∆х:

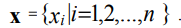szl7ncea-n2cb6qpgpooef9rrlc.png (3)

Граничные условия первого рода (условия Дирихле) для рассматривае­мой задачи могут быть представлены в виде:

wzd1ohqzrvar1rxwzbpuzvskgas.png (4)

где х1, xn — координаты граничных точек области [xmin, xmax]; g1, g2 — некоторые
константы.

Граничные условия второго рода (условия Неймана) для рассматривае­мой задачи могут быть представлены в виде:

v7e_jsncffbgg7oj0qgcfxhkoq8.png (5)

Проводя дискретизацию граничных условий Дирихле на равномерной координатной сетке (3) с использованием метода конечных разностей, по­лучим:

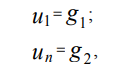qlz7rh-dairli3upqpepucctqq8.png (6)

где u1, un — значения функции u (x) в точках x1, xn соответственно.

Проводя дискретизацию граничных условий Неймана на сетке (3), по­лучим:

wbiaabrixia416dswku9qdrb0ew.png (7)

Проводя дискретизацию уравнения (2) для внутренних точек сетки, по­лучим:

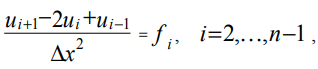lbx91o4els8rbssi999ixiup3hq.png (8)

где ui, fi — значения функций u (x), f (x) в точке сетки с координатой xi.

Таким образом, в результате дискретизации получим систему линейных алгебраических уравнений размерностью n, содержащую n — 2 уравнения вида (8) для внутренних точек области и уравнения (6) и (7) для двух граничных точек [1].

Ниже приведен листинг на Python численного решения уравнения (2) с граничными условиями (4) — (5) на координатной сетке (3).

Листинг решения 
from numpy import*
from numpy.linalg import solve
import matplotlib.pyplot as plt
x0=0#Начальная координата области решения
xn=5#Конечная координата области решения
n=100#Число точек координатной сетки
dx=(xn-x0)/(n-1)#Задание равномерной координатной сетки с шагом dx
x=[i*dx+x0 for i in arange(0,n,1)]#Задание равномерной координатной сетки с шагом dx
def f(i):#Функция правой части уравнения
         return 2*sin(x[i]**2)+cos(x[i]**2)
v1=1.0#Вид ГУ на левой границе (1 - Дирихле, 2 - Неймана)
g1=0.0#Значение ГУ на левой границе
v2=2.0#'Вид ГУ на правой границе (1 - Дирихле, 2 - Неймана)
g2=-0.5#Значение ГУ на правой границе
a=zeros([n,n])#Задание матрицы коэффициентов СЛАУ размерностью n x n
b=zeros([1,n])# Задание матрицы-строки свободных членов СЛАУ размерностью 1 x n
 #Определение коэффициентов и свободных членов СЛАУ,
# соответствующих граничным условиям и проверка корректности
#значений параметров v1, v2
b[0,n-1]=g1;
if v1==1:
         a[0,0]=1
elif v1==2:
         a[0,0]=-1/dx
         a[0,1]=1/dx;
else:
         print('Параметр v1 имеет неправильное значение')
b[0,n-1]=g2;
if v2==1:
         a[n-1,n-1]=1         
elif v2==2:
         a[n-1,n-1]=1/dx
         a[n-1,n-2]=-1/dx;
else:
         print('Параметр v2 имеет неправильное значение')
#Определение коэффициентов и свободных членов СЛАУ,
# соответствующих внутренним точкам области         
for i in arange(1, n-1,1):
         a[i,i]=-2/dx**2
         a[i,i+1]=1/dx**2
         a[i,i-1]=1/dx**2
         b[0,i]=f(i)
u=linalg.solve(a,b.T).T#Решение СЛАУ
def viz(v1,v2):
         if v1==v2==1:
                  return "ГУ  Дирихле на левой и ГУ Дирихле на правой  границе "
         elif v1==1 and v2==2:
                  return "ГУ  Дирихле на левой и ГУ Неймана на правой  границе "
         elif v2==1 and v2==1:
                  return "ГУ  Неймана на левой и ГУ Дирихле  на правой  границе "
plt.figure()
plt.title("График функции правой части уравнения Пуассона")
y=[f(i) for i in arange(0,n,1)]
plt.plot(x,y)
plt.grid(True)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.figure()
plt.title("График искомой функции уравнения Пуассона")
plt.xlabel('x')
plt.ylabel('u(x)')
plt.plot(x,u[0,:],label='%s'%viz(v1,v2))
plt.legend(loc='best')
plt.grid(True)
plt.show()


Получим:

rgcbsnh0xas1izeutmg48zpjoj4.png

eva3wn1cnai0vctjeuphffruzds.png

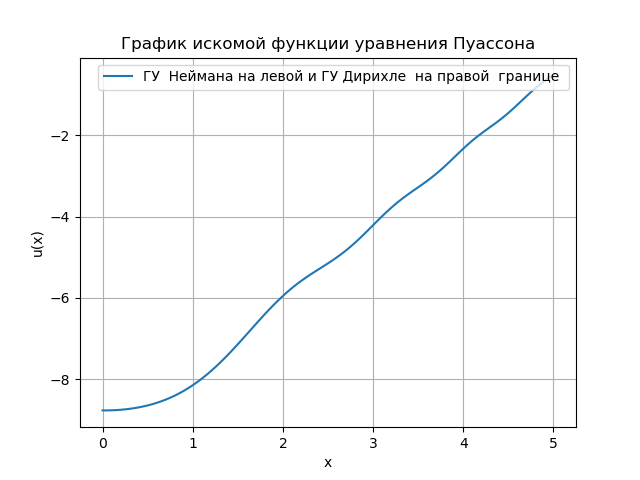
ie3gsqcgut9b9oaou1p1wlziduu.png

px4dsds2c4l1cpvzt3xfo9magvk.png

Разработанная мною на Python программа удобна для анализа граничных условий.Приведенный алгоритм решения на Python использует функцию Numpy — u=linalg.solve (a, b.T).T для решения системы алгебраических уравнений, что повышает быстродействие при квадратной матрице {a}. Однако при росте числа измерений необходимо переходить к использованию трех диагональной матрицы решение для которой усложняется даже для очень простой задачи, вот нашёл на форуме такой пример:

Пример решения с трёх диагональной матрицей 
from __future__ import print_function 
from __future__ import division 
import numpy as np 
import time 
ti = time.clock() 
m = 1000 
A = np.zeros((m, m)) 
B = np.zeros((m, 1))  
A[0, 0] = 1 
A[0, 1] = 2 
B[0, 0] = 1 
for i in range(1, m-1): 
    A[i, i-1] = 7 
    A[i, i] = 8  
    A[i, i+1] = 9 
    B[i, 0] = 2 
A[m-1, m-2] = 3 
A[m-1, m-1] = 4 
B[m-1, 0] = 3 
print('A \n', A) 
print('B \n', B) 
x = np.linalg.solve(A, B)  # solve A*x = B for x 
print('x \n', x) 
print('NUMPY time', time.clock()-ti, 'seconds')


Программа численного решения на равномерной по каждому направлению сетки задачи Дирихле для уравнения конвекции-диффузии

[2]

lwok-wgeshkjl9btqblywy2reoa.png (9)

Используем аппроксимации центральными разностями для конвективного слагаемого и итерационный метод релаксации.для зависимость скорости сходимости от параметра релаксации при численном решении задачи с /(х) = 1 и 6(х) = 0,10. В сеточной задаче:

_hmio5lokrlapgkzphgkej3jv_a.png (10)

Представим матрицу А в виде суммы диагональной, нижней треугольной и верхней треугольных матриц:

qkmdcimjicx_yvmpzz_-i92cuuy.png (10)

Метод релаксации соответствует использованию итерационного метода:

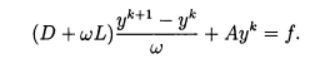r4zzum2ylgsk9813-24n1g_lvhg.png (11)

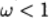При yuht8mbyk9lnpkeuaaohiyri6ls.png\ говорят о верхней релаксации, при yk_rp384zddromi8jgnmmtw_ijy.png — о нижней релаксации.

Листинг програмы 
from numpy import *
""" Численное решение задачи Дирихле
для уравнения конвекции-диффузии в
прямоугольнике.Метод релаксации."""
def relaxation(b, f, I1, I2, n1, n2, omega, tol = 1.e-8):
         h1 = I1 / n1
         h2 = I2 / n2
         d = 2. / h1**2 + 2. / h2**2
         y = zeros([n1+1, n2+1])
         ff = zeros([n1+1, n2+1])
         bb = zeros([n1+1, n2+1])
         for j in arange(1,n2,1):
                  for i in arange(1,n1,1):
                           ff [i,j] = f(i*h1, j*h2)
                           bb[i,j] = b(i*h1, j*h2)                           
         #максимальное число итераций - 10000
         for k in arange(1, 10001,1):
                  rn = 0.
                  for j in arange(1,n2,1):
                           for i in arange(1,n1,1):                                    
                                    rr = - (y[i-1,j] - 2.*y [i, j] + y[i+1,j]) / h1**2 \
                                         - (y[i,j-1] - 2.*y [i,j] + y[i,j+1]) / h2**2 \
                                         + bb[i,j]*(y [i+1,j] - y [i-1,j]) / (2.*h1) - ff [i,j]                                    
                                    rn = rn + rr**2
                                    y[i,j] = y[i,j] - omega * rr / d
                  rn = rn*h1*h2
                  if rn < tol**2: return y, k                  
         print ('Метод релаксации не сходиться:')
         print ('после 10000 итерации остаток=',sqrt(rn))
import matplotlib.pyplot as plt
bcList = [0., 10.]
sglist = ['-','--']
kk = 0
for bc in bcList:         
         I1 = 1.
         I2 = 1.
         def f(x,y):
                  return 1.
         def b(x,y):                 
                  return bc
         n1 = 25
         n2 = 25
         m = 20
         om = linspace(1., 1.95, m)
         it = zeros(([m]))
         for k in arange(0,m,1):
                  omega = om[k]
                  y, iter = relaxation(b, f, I1, I2, n1, n2, omega, tol=1.e-6)
                  it[k] = iter
         s1= 'b =' + str(bc)
         sg = sglist[kk]
         kk = kk+1
         plt.plot( om,it, sg, label = s1)
plt.title("Число итераций метода релаксации\n для приближённого решения эллиптической задачи\n с использованием заданного параметра релаксации $\\omega$")
plt.xlabel('$\\omega$')
plt.ylabel('iterations')
plt.legend(loc=0)
plt.grid(True)
plt.show(
)


Получим:

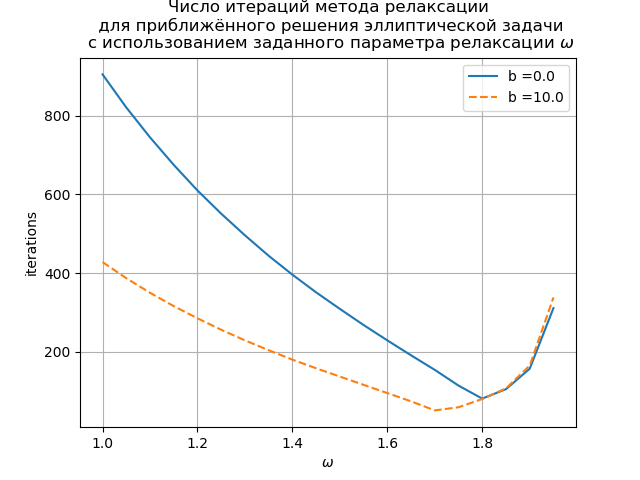
uwl5kestbhuztbnsnmh8joy8o2m.png

На графике показана зависимость числа итераций от параметра релаксации для уравнения Пуассона (b (х) = 0) и уравнения конвекции-диффузии (b (х) = 10). Для сеточного уравнения Пуассона оптимальное значении параметра релаксации находится аналитически, а итерационный метод сходиться при 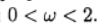hytqbzpded7xzlvqkdhxjdnhr_w.png.

Выводы:

  1. Приведено решение эллиптической задачи на Python с гибкой системой установки граничных условий
  2. Показано что метод релаксации имеет оптимальный диапазон (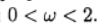hytqbzpded7xzlvqkdhxjdnhr_w.png) параметра релаксации.


Ссылки:

  1. Рындин Е.А. Методы решения задач математической физики. — Таганрог:
  2. Изд-во ТРТУ, 2003. — 120 с.
  3. Вабищевич П.Н. Численные методы: Вычислительный практикум. — М.: Книжный дом
  4. «ЛИБРОКОМ», 2010. — 320 с.

© Habrahabr.ru