Библиотека алгоритмов на графах на языке Go. Часть 111.12.2022 12:46

Предисловие

Приветствую тебя, дорогой читатель! Мне 21, я студент и младший Go-разработчик, а это — мой первый пост на Хабре. Недавно в компании с одногруппником мы решили взяться за амбициозный проект и я решил, что он, как никакой другой, подходит под первую статью. Проект заключается в создании библиотеки, содержащей основные алгоритмы на графах.

Библиотеку мы пишем на чистом Go по двум причинам:

Во-первых, нам нравится Go — это прекрасный язык без лишних усложняющих деталей и с минимум необходимого синтаксического сахара, ИМХО.

Во-вторых, мы не нашли по-настоящему удобной библиотеки для работы с графами на этом языке. Интересно попробовать без шпаргалок.

Введение

Для начала непосредственного погружения в реализации алгоритмов, нам необходимо быстренько пройтись по матчасти и напомнить, а кому-то рассказать о базовых понятиях.

Граф — это набор рёбер и вершин. — Самое простое определение, которое нам предлагает математика.

В принципе, если упростить, это правда так. Граф — это действительно математический объект, представляющий собой набор вершин и ребер, которые связывают эти вершины.

Рис.1 Ненаправленный граф, содержащий 8 вершин и 8 рёбер.Рис. 1 Ненаправленный граф, содержащий 8 вершин и 8 рёбер.

Видов графов есть масса, но в этой статье мы ограничимся четырьмя категориями:

  1. Взвешенный граф — у рёбер которого есть вес, означающий, например, расстояние между вершинами.

  2. Невзвешенный граф — вес рёбер не имеет значения и обычно в математических задачах берётся равным за единицу.

  3. Направленный граф — у рёбер которого есть направления.

  4. Ненаправленный граф — направлений у рёбер нет.

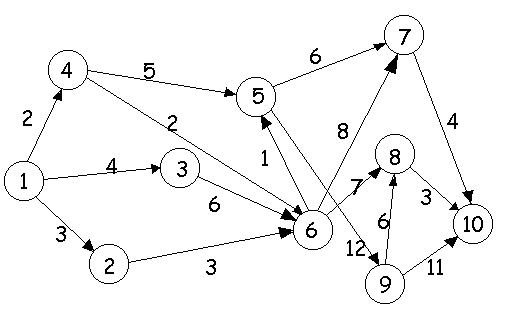Рис.2 Направленный взвешенный граф.Рис. 2 Направленный взвешенный граф.

Способы задания графа.

Кратко рассмотрим способы задания графа с помощью более примитивных математических объектов. Самые распространённые способы — список смежности и матрица смежности. Остановимся на первом подробнее.

Список смежности — один из способов представления графа в виде коллекции списков вершин. Каждой вершине графа соответствует список, состоящий из «соседей» этой вершины. — Определение из Википедии. Для полной ясности приведу пример. Список смежности для графа на Рис. 1 будет выглядеть следующим образом:

  • 1 — (2,5)

  • 2 — (1,3)

  • 3 — (2, 4)

  • 4 — (3,5,6)

  • 5 — (1,4)

  • 6 — (4,7)

  • 7 — (6,8)

  • 8 — (7)

Программная реализация

Итак, ознакомившись с матчастью я предлагаю перейти непосредственно к программной реализации, а именно — покажу, как наша реализация графа эволюционировала со временем.

Первый этап. Простейшая map.

Да, первым делом мы представили граф в виде обычной карты/словаря/отображения/мапы. Выглядело это следующим образом: 

package graph

type AbstractGraph struct {
  Graph map[string]map[string]int
}

Здесь в map ключом является строка — имя вершины, а значением — map, где ключ — имя вершины, а значение — вес ребра от родителя до данной вершины. В принципе, все стандартно, но при первом же детальном рассмотрении возникают вопросы и желание расширения: что, если мы захотим задать имя вершины целым числом, как в первом примере? Или точкой на карте? — это проблема номер 1.

Проблема номер 2 — в некоторых алгоритмах, которые будут рассмотрены далее в цикле статей, нам необходимо постоянно считать какие-то значения для наших вершин, например, её степень — количество её вершин-потомков или булевское/численное значение о том, что мы «прошли» эту вершину (например, в обходах), а также нам всё ещё необходимо хранить её имя.

З.Ы. конечно, можно решать эти проблемы непосредственно в алгоритмах. Например, «пройденные» вершины записывать в слайс и тд, но мы хотели максимально «выиграть» по памяти, или хотя бы постараться.

К чему мы пришли.

В итоге, наша структура переросла в нечто подобное: 

package graph

// T  comparable - имя ноды может быть только типом, поддерживающим операции сравнения
type Node[T comparable] struct {
    // Имя вершины
	Name  T
    // Флаг - 1 - помечена, 0 - не помечена 
	Mark  byte
    // Степень вершины.
	Power int
}

// AbstractGraph Абстрактное представление графа. Граф задан списком смежности в виде отображения (map) вершин. Вершины заданы структурами Node.
type AbstractGraph[T comparable] struct {
	Graph      map[*Node[T]]map[*Node[T]]int
	Vertexes   []*Node[T]
}

Да-да, мы решили использовать дженерики, введённые в Go 1.18 для использования в качестве имени вершины любой тип данных, поддерживающий операцию сравнения (comparable — сравнимый). Почему именно сравнимый — станет понятно далее.

Также, нам показалось, что не будет лишним написать функцию сборки такой структуры из map и отмены «пройденности» вершины. Для этого были написаны функции New и метод Unmark: 

package graph

// New - создаёт новую структуру AbstractGraph из переданной map.
func New[T comparable](graph map[T]map[T]int) *AbstractGraph[T] {
	output := make(map[*Node[T]]map[*Node[T]]int, len(graph))
	vertexes := make([]*Node[T], len(graph))
	g := &AbstractGraph[T]{Graph: output}
	i := 0
	for vert := range graph {
		n := &Node[T]{Name: vert, Mark: 0, Power: len(graph[vert])}
		vertexes[i] = n
		i++
	}
	for vert, list := range graph {
		var parentNode *Node[T]
		childList := make(map[*Node[T]]int, len(list))
		for _, v := range vertexes {
			if v.Name == vert {
				parentNode = v
				g.Graph[v] = childList
				break
			}
		}
		for vertex, weight := range list {
			for _, n := range vertexes {
				if n.Name == vertex {
					childList[n] = weight
				}
			}
		}
		g.Graph[parentNode] = childList
	}
	return g
}

// Unmark - устанавливает все пройденные вершины в изначальное состояние.
func (g *AbstractGraph[T]) Unmark() {
	for _, v := range g.Vertexes {
		v.Mark = 0
	}
}

Как-то так мы и начали наш путь, дальше — алгоритмы, из которых в данной статье мы рассмотрим только два самых базовых — обход/поиск в глубину и в ширину.

Алгоритмы обхода

В принципе, каждый разработчик обязан знать оба эти алгоритма обхода хотя бы в теории, но не будет лишним в паре фраз объяснить суть.

И начнем мы с обхода (поиска) в глубину.

При поиске/обходе в глубину, мы идем по вершинам «вглубь» графа (неожиданно, не правда ли?). Проще говоря, мы на каждом шаге просматриваем одну вершину, смежную данной и переходим к ней. В случае, когда мы наталкиваемся на пройденную ранее вершину, мы возвращаемся и идем по другому ребру.

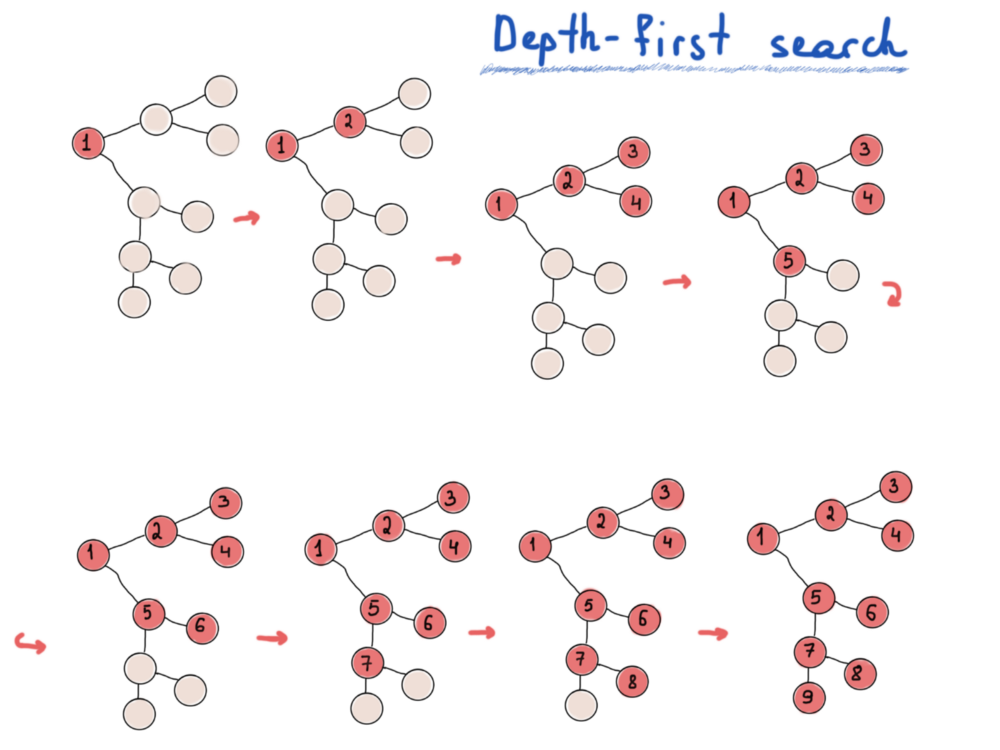Рис.3 Иллюстрация поиска / обхода в глубину.Рис. 3 Иллюстрация поиска / обхода в глубину.

Сразу стоит пояснить, поиск отличается от обхода заданием условия. При поиске мы обходим граф в поиске какой-то конкретной вершины, а при обходе…просто обходим все вершины графа. В качестве «условия» будем передавать в сигнатуру метода добавим функцию compare, возвращающую bool. При обходе просто будет передавать функцию, возвращающую false.

Обход в глубину основан на стеке. Смысл простой: мы добавляем в стек стартовую вершину, после чего запускаем цикл, пока не опустеет стек. на каждом этапе мы берём из стека его вершину и применяем к данной вершине переданную функцию compare. Если if отрабатывает, то мы возвращаем список (слайс) пройденных вершин и true — вершина найдена. В обратном случае, добавляем в стек все вершины, смежные данной, добавляем эту вершину в список пройденных и, наконец, помечаем её как пройденную.

Собственно, сам код: 

// DFS Поиск в глубину.
func (g *AbstractGraph[T]) DFS(start T, compare func(want T) bool) ([]*Node[T], bool) {
	var searchStack []*Node[T]
	for vert := range g.Graph {
		if vert.Name == start {
			searchStack = append(searchStack, vert)
			break
		}
	}
	for len(searchStack) != 0 {
		var vertex = searchStack[len(searchStack)-1]
		searchStack = searchStack[:len(searchStack)-1]
		if vertex.Mark != 1 {
			if compare(vertex.Name) {
				g.Unmark()
				g.Vertexes = append(g.Vertexes, vertex)
				return g.Vertexes, true
			}
			vertex.Mark = 1
			g.Vertexes = append(g.Vertexes, vertex)
			searchStack = append(searchStack, g.GetAdjacentVertices(vertex)...)
		}
	}
	g.Unmark()
	return nil, false
}

Обход/поиск в глубину:

В общем-то, в алгоритме происходит всё то же самое, только вместо того, чтобы идти «вглубь» графа, мы сначала идем по всем вершинам, смежным данной, после чего переходим к следующей, и вместо стека используем очередь.

Рис.4 Иллюстрация поиска / обхода в ширину.Рис. 4 Иллюстрация поиска / обхода в ширину.

Ну и сам код: 

// BFS Поиск в ширину
func (g *AbstractGraph[T]) BFS(start T, compare func(want T) bool) ([]*Node[T], bool) {
	var searchQueue []*Node[T]
	for vert := range g.Graph {
		if vert.Name == start {
			searchQueue = append(searchQueue, vert)
			break
		}
	}
	for len(searchQueue) != 0 {
		var vertex = searchQueue[0]
		searchQueue = searchQueue[1:]
		if vertex.Mark != 1 {
			if compare(vertex.Name) {
				g.Unmark()
				g.Vertexes = append(g.Vertexes, vertex)
				return g.Vertexes, true
			}
			vertex.Mark = 1
			g.Vertexes = append(g.Vertexes, vertex)
			searchQueue = append(searchQueue, g.GetAdjacentVertices(vertex)...)
		}

	}
	g.Unmark()
	return nil, false
}

Заключение

Было бы очень приятно услышать фидбэк от сообщества: какие есть недочеты в проекте, что мы упустили или сделали неправильно. Хочется создать хороший опенсорс проект, который не стыдно будет представить публике.

Ссылка на GitHub-репозиторий

© Habrahabr.ru