Белый шум рисует черный квадрат. Часть 2. Решение
В первой публикации рассказывалось о том, что есть подзабытая теорема Эрдёша-Реньи, из которой следует, что в случайном ряде, длины N, с вероятностью близкой к 1 существует подряд из одинаковых значений длиной \log_2{N}. Указанное свойство случайной величины можно использовать для ответа на вопрос: «После обработки больших данных, подчиняется ли остаточный ряд закону случайных чисел или нет?»
Ответ на такой вопрос определялся не на основании тестов соответствия нормальности распределения, а на основании свойств самого остаточного ряда.
По присутствию или отсутствию, либо смещению частотности подрядов одинаковых символов. Попытался в публикации, показать возможности применения этого инструмента, хотя возникало много вопросов, как это работает в реальности, при проведении анализа в больших данных. Но дискуссия была результативной, а пользователь VDG, даже представил реальный пример:»… Дендритные ветки нейрона можно представить как битовую последовательность. Ветка, а затем и весь нейрон, срабатывает, когда в любом её месте активируется цепочка синапсов. У нейрона есть задача не срабатывать на белый шум, соответственно, минимальная длина цепочки, насколько помню было у Нументы, равна 14 синапсам у пирамидального нейрона с его 10 тысячами синапсов. И по формуле получаем: \log_2{10000} = 13,287. То есть, цепочки длиной меньше 14 будут возникать из-за естественного шума, но не будут активировать нейрон. Прямо вот идеально легло».
Попробуем рассмотреть представленный механизм в этом материале.
В первой публикации было поставлено много вопросов. Попробуем уточнить механизм работы теоремы Эрдёша-Реньи в этой статье.
Решение обнаружилось в связи с парадоксом «Игра Пенни». Игра заключается в следующем — два игрока А и Б собираются выбрасывать пять раз монету, присваивая, допустим, «орлу» — 1, «решке» — 0. Игрок А выбирает последовательность из трех значений и озвучивает ее, предположим — 001.
Игрок Б выбирает свою последовательность, предположим 100. Выигрывает тот игрок, последовательность которого выпадает первой. Допустим, выпало 01001, то есть 0–100–1, что соответствует выбору Б. Парадокс «Игры Пенни» заключается в том, что какую бы не выбрал последовательность игрок А, у игрока Б всегда есть возможность выбора последовательности, вероятность выпадения которой, больше чем у последовательности выбранной игроком А. Матрица выигрыша игрока Б представлена на рисунке 1.

Рис. 1. Матрица выигрышей игрока Б в «Игре Пенни» при пяти бросаниях.
Эффект этого парадокса заключается в том, что случайный ряд не транзитивен, то есть если U>R, а R>Q, то это не означает, что Q>U.
Следствие этого парадокса, заключаются в следующих обыденных вещах, если игрок играет по правилам и соблюдает законы теории вероятности:
- В азартных играх обычно побеждает, тот чья касса больше — «задавить банком».
- В казино выигрывает только казино.
- При игре на бирже только удача определяет, сколько времени продержится трейдер, пока не проиграет свой капитал.
Физический смысл этого закона, на котором основан парадокс «Игры Пенни» заключается в том, что преимущество имеет тот, кто больше может продолжать случайную последовательность. Как в первом примере — игрок, у которого наличности больше. Во втором варианте — казино играет с сотнями последовательностей одновременно, и будет продолжать играть после того, как любой из игроков прекратит игру. А игра против биржи одного игрока, не идет в сравнение, с миллионами операций на бирже.
Как видим, первый закон нарисовался — BigData определяет ситуацию в сравнении с локальной информацией.
Второй определяющий момент — отсутствие свойства транзитивности у случайных последовательностей. Следствием этого является невозможность откатить ситуацию обратно.
Дальше выдвину гипотезы при анализе BigData:
1) Понимание развивающихся событий возможно, только на таком объеме, в котором зафиксированы последствия исследуемых событий. Механизм для данного процесса можно представить следующим образом. Поле случайности — это поле, в котором несколько потенциальных процессов пытаются себя реализовать. После реализации себя, процесс оставляет изменения, и степень следов от произошедших процессов мы и пытаемся обнаружить. Зависимости определяются уже по величине доли оставленных результатов. К вышесказанному поясню, что, на мой взгляд, то, как происходят сами преобразования, в настоящий момент, наука не может дать формального определения. Если бы, эти определения были, то некоторые парадоксы Зенона, перестали бы быть парадоксами, да и единство и борьба противоположностей, материалистической диалектики, перестал бы быть, в ней постулатом.
Предполагаю, что не стоит ломать копья утверждений о том, что если мы определяем постфактум процесс, то это бессмысленное занятие, так как следующий процесс будет непредсказуем. Человек видит достаточно локально, а процессы BigData могут длиться миллиардами лет, поэтому возможность увидеть механизм какого-то процесса, из поля BigData, у нас есть. Интересный материал по большим значениям вселенной, представлен тут.
2) Вторая гипотеза, которая может быть выведена из отсутствия свойства транзитивности — это влияния интервала и условий на изучаемый процесс. То есть, с одной стороны, есть координата по времени, которая позиционирует исследуемый процесс, и, шанс повторить условия, в которых формировался наш процесс, и были получены миллионы записей, уже практически невозможно. С другой стороны, законы комбинаторики игнорировать нельзя. Эти законы нам говорят, что вероятность выпадения определенной комбинации должна существовать всегда. На рисунке 2 представлено распределение вариантов цепочек из N сигналов в которых существуют ряды из субрядов длиной k. Общая сумма больше чем \2^N, так как короткие цепочки находятся в сочетании с более длинными.
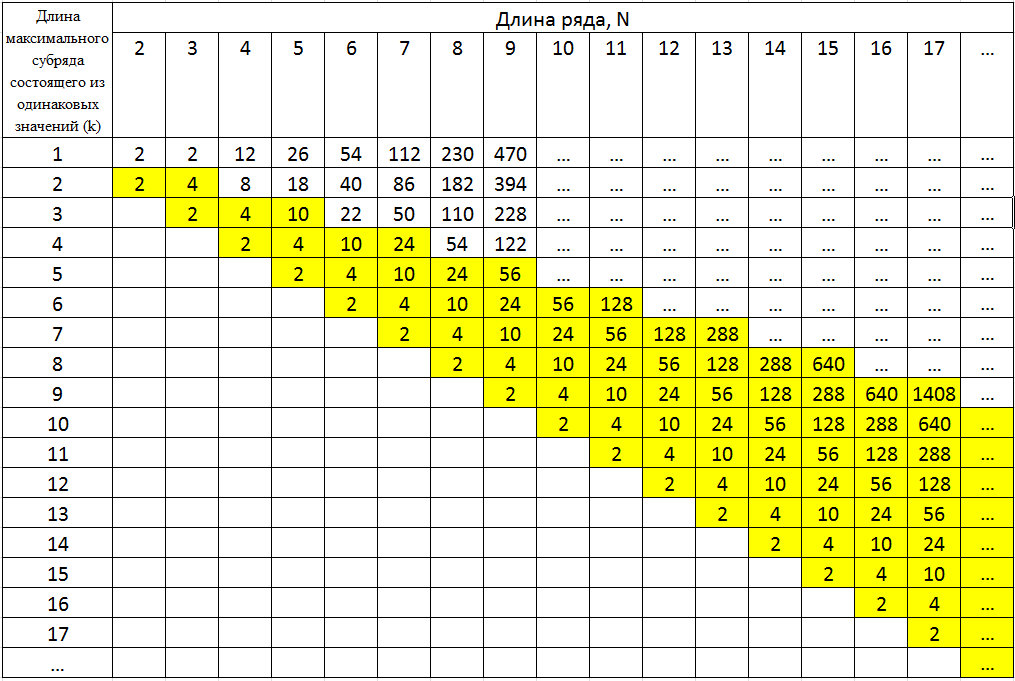
Рис. 2. Число возможных вариантов субряда из k одинаковых сигналов, в последовательности из N значений.
Для вариантов, в которых присутствуют цепочки длиной более N/2, они залиты желтым, их количество определяется достаточно несложным образом по формуле:

То есть соответствующие вероятности, для рядов содержащих цепочки из k>= N/2 одинаковых значений (вероятность ряда состоящего из N значений описывать не будем), будет определяться формулой:
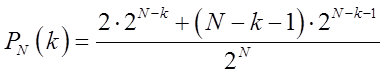
По ходу обсуждения, в первой части, возникали вопросы, суть которых сводилась к следующему: «А где границы белого шума?» Тут рассматривая таблицу рисунка 2, сформировалась гипотеза для обсуждения, по следующей схема.
Опираясь на интегральную теорему Муавра-Лапласа:

Определим интервалы для Ф (1,96 = 95% вероятности:

Если посмотреть, то таблица на рисунке 2 отражает полное поле вероятностей, с другой стороны параметры распределения в каждом случае однозначно определимы, и представлены на рисунке 3, где покажем их на примере ряда из 9 значений. Так как количество вариантов \2^9{= 512}, и для этого числа испытаний и будем находить альфа.

Рис. 3. Границы интервалов вероятности субрядов длин k одинаковых сигналов, в последовательности из 9 значений, с надежностью 2 сигма (95%).
На рисунке 4 представил интервалы для случайной величины, где рис 4 б, транспонированный рисунка 4а.

Рис. 4. Интервалы случайной величины для каждого субряда, с надежностью 95%.
Чтобы каким-то образом структурировать ответы на вопросы где находится белый шум, сформулировал существующие подходы следующим образом:
- Белый шум признан сообществом;
- Данные, которые можно формулировать аналитическими выражениями;
- Информация, структурируемая нейронными сетями;
- Кубиты, квантовых компьютеров;
- BigData;
- Если существуют большие данные, то вполне возможно, что существуют гиперданные.
Для предложенной структуризации подсказкой оказалась идея Филатова О. В. «Определение случайной бинарной последовательности, как комбинаторного объекта. Расчёт совпадающих фрагментов в случайных бинарных последовательностях» о поведении фрагментов последовательности напоминающей поведение частиц в микромире.
Кубиты, которые имеют трехмерную структуру, предполагали, что структурная схема должна иметь трехмерную модель. Несколько слоев, которые признаны сообществом, подразумевали многослойность и соединяя все это, наиболее элегантная схема возможна в форме тороида, рисунок 5.

Рис. 5. Предположение о структуре данных в отображении на пространство случайных величин (картинки взяты из сети Интернет).
Развивая рассуждения дальше обратим внимание, что на рисунке 3, все частоты являются четными числами. Это является следствием симметричности данных »0–1». Симметричность случайных данных отражена в «Постулатах Голомба» Соломона Вольфа Голомба. Опираясь на исследования Филатова О.В. «Вывод формул для постулатов Голомба. Способ создания псевдослучайной последовательности из частот Мизеса. Основы «Комбинаторики длинных последовательностей» используется понятие полуволна. Считаю, что данный аспект существенен при исследовании белого шума, так как связан с такими параметрами как, длина ряда.
С учетом свойств случайных процессов, волна белого шума может приобретать различные свойства, в том числе отсутствие симметричности волн и возможное несоблюдение теоремы Нётер. Но существуют процессы в физическом мире как образование пены волны прибоя, рисунок 6. А значит допускать необычные параметры волн белого шума у нас есть все основания.
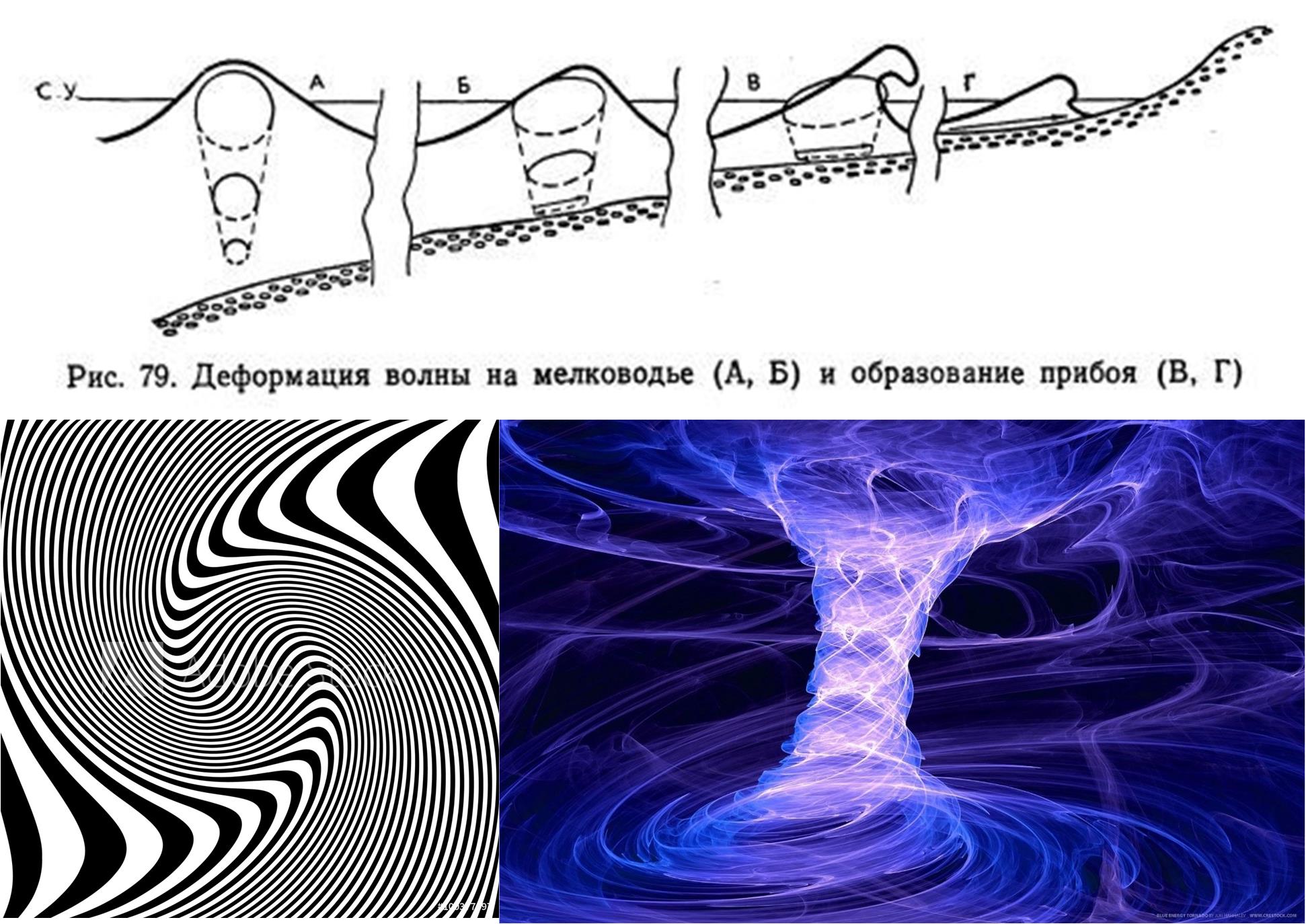
Рис. 6. Механизм деформации волн у берега и примеры процессов, которые при проекции на некоторые гиперплоскости, локальном пространстве, могут выглядеть как отображение случайного процесса (картинки взяты из сети Интернет).
Переходя к практической части, подведу итоги предложенных подходов при работе с белым шумом.
- Отсутствия свойства транзитивности в случайных процессах.
- Предположение, что свойства симметрии в белом шуме являются реализацией свойств симметрии процессов высших, чем рассматриваемый процессов текущей ситуации.
- Локальность случайных процессов. Эта предпосылка явно в публикации не показана, но достаточно хорошо вписывается в рамках конструктивной математики. Вы все пользуетесь ею (конструктивной математикой), когда пишите скрипт, в котором устанавливается требование обратиться к ячейке памяти и прочитать ее содержимое. Так как по умолчанию вы подразумеваете, что в этой ячейке находится определенное значение 0 или 1 и ничего другого там быть не может. Неплохой материал для ознакомления с ее подходами представлен здесь: Н.Н. Непейвода «Конструктивная математика: обзор достижений, недостатков и уроков. Часть I».
Практическая часть
В первой части рассматривался вопрос теоремы Эрдёша-Реньи, который заключался в том, что данная теорема была найдена только в одном источнике, которое является переводным с венгерского, эта книга была опубликована еще в СССР и каких-то подтверждений или упоминаний о ней обнаружено не было. Как следствие этого факта существовала неопределенность вообще ее существования и тем более применения.
В результате поисков было обнаружено в работе Филатова О.В. «Вывод формул для постулатов Голомба. Способ создания псевдослучайной последовательности из частот Мизеса. Основы «Комбинаторики длинных последовательностей» стр. 15 следующее, рисунок 7, привожу оригинал из материала.

Рис. 7. Оригинал части публикации Филатова О.В. «Вывод формул для постулатов Голомба. Способ создания псевдослучайной последовательности из частот Мизеса. Основы «Комбинаторики длинных последовательностей».
Теорема Эрдёша-Реньи сформулирована следующим образом:
При бросании монеты N раз, серия выпадения одинаковых сторон монеты подряд длины \log_2{N} наблюдается с вероятностью, стремящейся к 1, при N стремящемся к бесконечности.
Запишем теорему в формулировках «Комбинаторики длинных последовательностей» для одной стороны монеты:

Проведем доказательство:

Как видно частоты Мизеса для цуги состоящей из цепочки одинаковых сигналов длиной n = \log_2{N} совпадают с выводами теоремы Эрдёша-Реньи о вероятности этой же цепочки в случае случайного ряда. А значит можно отмести сомнения и признать ее существование и возможность применения.
Так как публикация получилась уже больше рекомендуемой маркетологами, то продолжение в следующей части «Белый шум рисует черный квадрат. Часть 3. Применение».
