[recovery mode] Кластерная память с аппроксимацией10.08.2019 02:04

Разработана память с нелинейной аппроксимацией внутри кластеров данных. Кластеры предлагается выделять методом k-средних. Аппроксимацию проводить с помощью обучения ансамбля нейронных сетей. Кластерная память протестирована на примере адаптивного фильтра для преобразования цветов изображения. По результатам компьютерных экспериментов данный вид памяти показал хорошую селективную способность к обучению. На примере адаптивного фильтра удается обучить память к изменению всей цветовой палитры изображения.
Введение

Существенным недостатком нейронных сетей перцептронов является их плохая способность к обобщению многокластерных данных. В частности задача XOR для обучения логической функции не может быть решена с помощью одного перцептрона, поскольку в одном направлении точек данных прослеживается два противоречивых тренда на возрастание и убывание решающей функции нейронной сети. Такие противоречивые зависимости в пределах одного массива обучающих данных не могут быть обобщены одной нейронной сетью вида многомерного перцептрона. Поэтому предлагается разбивать массив обучающих данных на кластеры в пределах которых проводить аппроксимацию отдельными нейросетями. В статье проводится компьютерный эксперимент по апробации данного типа памяти к задаче адаптивного фильтра изображения для селективного преобразования цветовой палитры.

Кластерный анализ: метод k-средних

Метод k-средних является одним из наиболее популярных методов кластеризации. Его целью является получение таких центров данных, которые бы соответствовали бы гипотезе компактности классов данных при их симметричном радиальном распределении. Одним из способов определить положения таких центров, при заданном их количестве k, является EM подход.

В данном методе выполняется последовательно две процедуры.

Определение для каждого объекта данных $X_{i}$ ближайшего центра $C_{j}$ , и назначение данному объекту метки класса $X_{i}^{j}$ . Далее для всех объектов становится определена их принадлежность различным классам.
Вычисление нового положения центров всех классов.

Итеративно повторяя эти две процедуры из начального случайного положения центров k классов, можно добиться разделения объектов на классы, которые бы максимально бы соответствовали гипотезе радиальной компактности классов.

С методом k-средних будет сравниваться новый авторский алгоритм классификации.

Основные цвета изображения

Метод k-средних примененный к пространству цветов пикселей изображения, позволяет выделить основные тона. Для этого предлагается преобразовать цвета пикселей RGB в схему HSB методом платформы Java Color.RGBtoHSB и получить оттенок цвета H и яркость B. Расстояние между пикселями в цветовом пространстве предлагается определять по формуле:

$dist\left(X_{i} ,X_{j} \right)=\sqrt{H_{i} \cdot B_{i} -H_{j} \cdot B_{j} }$

Начальное расположение центров кластеров предлагается вычислять следующим образом.

Найти min и max значения $H_{i} \cdot B_{i}$ для всех пикселей.
Разделить интервал [min, max] на k частей.
Вычислить частоты пикселей в каждом подинтервале по значению $H_{i} \cdot B_{i}$ .
Отсортировать подинтервалы по количеству пикселей по убыванию.
Вычислить центры пикселей в подинтервалах.

Кластерный анализ: карта градиентов

Подход для проведения кластерного анализа на базе метода k-средних обладает недостатком, заключающемся в отсутствии влияния показателей выходного образа. Чтобы учесть изменение показателей выходного образа в зависимости от изменения показателей входного образа предлагается следующий алгоритм.

Отсортировать все входные вектора по величине $H_{i} \cdot B_{i}$
При переходе от одного входного вектора к другому в отсортированном массиве просмотреть изменение монотонности величины $H_{i} \cdot B_{i}$ соответствующих выходных векторов.
Входные вектора с изменением монотонности $H_{i} \cdot B_{i}$ соответствующих выходных векторов не большими выбранного порога p отнести в один класс.
Порог p можно варьировать для разбиения векторов на нужное число кластеров.

Адаптивный фильтр

Для осуществления преобразования изображений возможно применения нейронных сетей. Главным преимуществом нейронных сетей является их автоматическая способность к обучению. В данном случае предлагается для обучения адаптивного фильтра [Шовин 2018] на базе нейронной сети использовать пару изображений, в которой исходное изображение является образцом, а второе является измененным от образца каким либо существующим фильтром или преобразованием. Адаптивному фильтру необходимо восстановить это преобразование. Для этого используется окно размером dx на dy и 3 цветовых канала. В результате в нейронной сети используется dx•dy•3 входных сигналов для входных нейронов. Сеть может дополняться скрытыми слоями из количества нейронов сопоставленных цветовым факторам преобразования фильтра. На выходе нейрона предлагается использовать 3 нейрона, выходные сигналы которых ставятся в соответствие трем цветам (rgb — красный, зеленый, синий) в центральном пикселе окна из выходного изображения. Сигнал цветового канала пикселя приводится линейным преобразованием в диапазон значений [-0,5; 0,5]. Тогда как в качестве передаточной функции нейронов сети используется антисимметричная сигмойдная функция с интервалом значений [-1; 1]. Для граничных пикселей изображений, когда окно выходит за рамки изображений, на входные значения нейронов сети, соответствующие таким пикселям ставятся 0. Нейронная сеть обучается на окнах для всех пикселей выходного изображения по методу обратного распространения ошибки.

Кластерная память

После того когда найдены основные тона изображения, для пикселей каждого тона строится адаптивный фильтр с шириной и высотой окна в 1 пиксель. Фильтры обучаются для каждого кластера отдельно. Тем самым с помощью нейронных сетей адаптивных фильтров осуществляется аппроксимация цветов пикселей в пределах своего кластера (тона).

Численный эксперимент

Проведено обучение кластерной памяти на примере адаптивных фильтров для преобразования цветовой палитры.

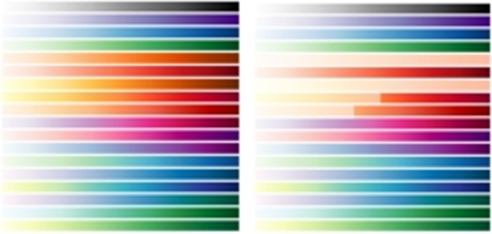
Рис. 1. Оригинальная и измененная палитра.

Адаптивному фильтру требуется научиться селективно отбеливать цвета кожи при этом не изменять других цветов.

В результате применения адаптивного фильтра с кластерной памятью (9 кластеров-тонов и кластеры по карте градиентов) к исходной палитре получены следующие изображения:

Рис. 2. Измененная палитра по основным тонам и по карте градиентов.

Заключение

Предложен подход для обучения сложным функциям на базе кластерной памяти с аппроксимацией с помощью семейства нейронных сетей и проведения кластерного анализа исходных данных. На примере адаптивного фильтра показана возможность селективного преобразования цветов палитры. Использование кластерной памяти с аппроксимацией актуально когда в обучающем наборе данных прослеживаются противоречивые тренды в одинаковых направлениях изменения показателей исходных данных. В частности оказывается возможным решить задачу XOR для обучения логической функции.

Список литературы

Шовин В.А. Адаптивный фильтр изображений на базе нейронной сети. // Математическое и компьютерное моделирование: сборник материалов VI Международной научной конференции. 2018. — 198 с.