Автоматное программирование: определение, модель, реализация
1. Введение
Термин »автоматное программирование» (АП) был введен в широкую практику в 90-х годах прошлого века [1, 2], хотя о применении автоматов в программировании шла речь задолго до этого. R первым упоминаниям уже начала 70-х годов можно отнести метод введения переменной состояния или, по-другому, метод преобразования неструктурированных программ Ашкрофта и Манны [3]. За прошедшее время сформировалось достаточное число его поклонников и не меньшее число критиков. Если говорить об их разногласиях, то в их основе отсутствие формального определения АП и поверхностное восприятие его возможностей. Из-за этого автоматное программирование формируется интуитивно, что и приводит к противоречивым его формам, порой, мало похожим на первоисточник — модель конечного автомата.
Но, несмотря на пробелы в теории, создано множество вариантов технологий автоматного программирования. Это, например, SWITCH-технология, которая известна, в том числе, и по активному продвижению АП, пакет Stateflow [4] системы MATLAB [5], язык UML [6], различные реализации автоматов в рамках программных библиотек типа Qt [7] и т.д. и т.п. Эту же технологию реализует и среда автоматного Визуального Компонентного Программирования — ВКПа[8].
По большому счету автоматному программированию необходим и свой «автоматный язык». Пока же его роль выполняют существующие языки. Реализация АП в них строится на базе достаточно простых, если не сказать — примитивных, программистских приемах и SWITCH-технология тому показательный пример. Но такой, слишком простой, подход влечет утрату важных качеств модели. Подобное программирование, порой, лишь имитирует в той или иной мере возможности АП. Тем не менее, данный вариант наиболее типичен, т.к. позволяет обойтись без специализированного языка.
В наши цели входит определение автоматного программирования, описание его вычислительной модели и принципов ее реализации. Рассматриваемые далее примеры, которые в той или иной мере это демонстрируют, созданы в рамках программных сред MATLAB и ВКПа. Первая — наглядно демонстрирует возможности визуального программирования на базе автоматной модели, вторая — пример наиболее полного воплощения идей автоматного программирования и реализации автоматного языка на базе С++ без утраты каких-либо качеств базовой модели.
2. Формальная модель автоматного программирования
Ответ на наиболее часто задаваемый вопрос, что собой представляет автоматная программа, казалось бы, достаточно прост. Как минимум, в большинстве языков программирования на структурном уровне выделяют: 1) данные, 2) операции и 3) управление. В соответствии с этим схематология [9] представляет модель программы в форме схемы программы тройкой S = (M, A, C), где M — конечное множество элементов памяти, называемых переменными, A — конечное множество операторов, C — управление [10]. Под элементами памяти будем понимать также более сложные объекты — массивы, очереди, множества, стеки и т.п., а к операторам будем относить, кроме простейших операций, программные функции.
Определение 1. Автоматной программой (АП) будем называть программу с моделью управления в форме модели конечного автомата.
Данное определение отличает АП от других определений программ моделью управления. В нашем случае она может быть представлена аналитической, графической, матричной или любой другой формой задания автоматов (подробнее о способах задания см. [11]). Но существенным при этом является реализация всех свойств автоматной модели управления, выраженном в ее законе функционирования, а не только лишь демонстрация «картинок», как это декларирует SWITCH-технология.
Весьма полезным свойством автоматной модели можно считать использование понятия текущего состояния программы в качестве объекта для синхронизации процессов, отслеживания хода вычислений, отладки и т.д. и т.п. Автоматическая его установка упрощает алгоритмы, уменьшает число операторов и повышает надежность программирования. Например, исключаются типовые ошибки, связанные с использованием, так называемых, флагов (достаточно подробно проблему флагов освещает SWITCH-технология).
Для связи модели управления с остальными компонентами структурной модели поставим в соответствие множеству каналов управления С операторы из множества A. Пусть входным каналам соответствуют предикаты — функции, выполняющие [только] анализ элементов множества M и возвращающие булевское значение, а выходным каналам действия — функции, выполняющие преобразования элементов множества М не имеющие возвращаемого значения.
Описанные далее изменения модели КА делают автоматную модель адекватной поставленным задачам, особенно для систем параллельного типа. Более того, именно решение вопросов параллельного программирования определяет, чуть ли не основной смысл внедрения автоматного программирования, т.к. существующее параллельное программирование с этим справляется с весьма большими проблемами.
3. Конечный автомат с абстрактным состоянием. Автоматы Мили и Мура
Для эффективного использования классический конечный автомат (КА) нуждается в изменениях. К ним относится введение в модель вложенной иерархии, которую в обычных программах отражают подпрограммы, описание и реализация параллелизма процессов, представленные нынче многопоточным и многоядерным программированием, корутинами, внедренными буквально насильно в языки программирования. Но такие темы, как вложенная иерархия и параллелизм, классической теорией, к сожалению, фактически не рассматриваются.
Начнем с формулировок, затрагивающих на начальном этапе просто отдельный конечный автомат. Именно он в дальнейшем станет базовой компонентой для более сложной многокомпонентной параллельной модели.
Определение 1. Назовем автоматом с абстрактным состоянием конечный автомат, у которого каналы представлены множеством входных — x1, x2, …, xn и выходных — y1, y2, …, ym булевых переменных, а внутреннее состояние — одной многозначной переменной q (см. также [12]). Его функция переходов определяет следующее состояние q (t+1) в зависимости от текущего значения состояния q и значения двоичной входной переменной, представленной булевой функцией — f (x1, x2, …, xm) от входных переменных в дизъюнктивной нормальной форме (ДНФ). Функция выходов автомата определяет зависимость последующего значения выходной переменной y(t+1), представленной элементарной конъюнкцией — (y1, y2, …, yn) выходных булевых переменных без знаков отрицания, в зависимости от текущего состояния q и текущего состояния входных каналов x(t). Закон функционирования автомата определяется уравнениями:
q (t+1) = j (q (t), x(t)), (1)
y(t+1) = y (q (t), x(t)),
Подобные автоматы будем называть просто конечными автоматами (КА) или, автоматами Мили. Необходимо также отметить, что именно о таком же поведении (законе функционирования) автоматов говорит и М.Минский [14].
Отсутствие входной булевой переменной в простой конъюнкции ДНФ означает игнорирование состояния соответствующего входного канала при вычислении условия перехода. Соответственно при этом не нужно запускать и предикат, который сопоставлен данному каналу. Отсутствие выходной булевой переменной на переходе означает отсутствие соответствующего выходного сигнала и запуска сопоставленной ему функции-действия.
Существенной особенностью приведенного закона функционирования КА является привязка выходных каналов автомата к следующему моменту времени подобно изменению внутреннего состояния. Это исключает мгновенную реакцию автомата на текущее изменение сигналов входных каналов. Так моделируется свойство инерционности, присущее всем реальным системам.
Определение 2. Инерционным законом функционирования автоматов будем называть закон, который связывает выдачу выходного сигнала автомата со следующим по отношению к текущему времени тактом дискретного времени.
В классической теории автоматов входные и выходные сигналы связаны с текущим моментом времени t и из-за этого между ними возникает «мгновенная» связь. Это противоречит признаваемому даже в теории факту, что в реальной ситуации выходной сигнал y (t) автомата всегда появляется после входного сигнала x (t) (см., например, [11]). Инерционный закон устраняет необходимость также различать, как это принято в теории, обычные и сдвинутые функции выходов.
Отметим, что приведенное определение конечного автомата вводит новый вид автоматов, которые по форме ни чем не отличаются от своих классических аналогов, но имеют свой закон функционирования. И, пожалуй, только у автоматов изменение закона функционирования качественным образом влияет на свойства формальной модели.
Качественная сторона нового закона функционирования проявляется в первую очередь в возможностях автоматов для описания и реализации систем параллельного типа. В теоретическом же плане учет инерционности позволяет справиться с проблемами, которые не имеют решения в рамках классической теории автоматов. К ним относится проблема корректности схем, включающих циклические цепи [13].
Определение 3. Назовем автоматом Мура автомат, у которого функции переходов и выходов следующие:
q (t+1) = j (q (t), x(t)), (2)
y(t+1) = y (q (t)).
У автоматов Мура значение выходной переменной зависит только от переменной внутреннего состояния. Подобные автоматы называются правильными (подробнее см. [11]). Напомним, что в классической теории автоматами Мура называют правильные автоматы второго рода, выходной сигнал которых определяется ровно в момент t от состояния q (t), которое, что примечательно, в этот же момент еще только вычисляется (подробнее см. [11]).
Определение 4. Назовем совмещенным автоматом Мили-Мура автомат, функции переходов и выходов которого определяются следующим образом:
q (t+1) = j (q (t), x(t)), (3)
y1(t+1) = y1(q (t), x(t)),
y2(t+1) = y2(q (t)).
Данная модель совмещает в себе, как функции автоматов Мили, которым соответствует функция выходов y1(t+1), так и автоматов Мура — y2(t+1).
Может показаться, что автоматы Мили и Мура имеют разное поведение: автомат Мили выдает сигналы до момента изменения текущего состояния, а автомат Мура — после его изменения. Но на самом деле это не столь принципиально, т.к. выдача выходного сигнала и установление нового состояния должны быть выполнены до наступления следующего момента дискретного времени.
Таким образом, для внешнего наблюдателя, который воспринимает лишь границы дискретных моментов времени отличить работу автоматов Мили от автоматов Мура невозможно. Но, во-первых, это важно с точки зрения описания модели, т.к. форма автоматов Мура исключает повторы сигналов на переходах в текущее состояние. А, во-вторых, на это нужно обратить внимание при реализации данных моделей, когда на текущем дискретном такте необходимо обеспечить завершение всех автоматных операций, связанных с выдачей сигналов и изменением текущего состояния до момента наступления очередного такта автоматного времени.
Веденный закон функционирования автоматов учитывает инерционность, присущую всем реальным объектам, как равно тем же программам. Именно такая форма закона снимает все ограничения на любые структурные схемы, включая алгебраические контура, циклические цепи, обратные связи и их аналоги. Сразу же отметим, что в этом случае речь идет, конечно же, о моделях параллельного типа, детального рассмотрения которых классическая теория, похоже, избегает.
Тем не менее, проблемы не исчезают и в рамках классической теории на примере схемы на рис. 1 (цепь из трех автоматов-инверторов) часто демонстрируют [теоретическую] проблему неоднозначности сигналов [13]. В рамках инерционного закона ее не существует в принципе. Для этого только необходимо, чтобы при реализации параллельной автоматной модели 1) все автоматы схемы, работая в едином дискретном времени, 2) выполняли бы сначала анализ текущих входных сигналов, текущего состояния и только затем их изменяли в соответствии с функциями переходов/выходов.
Рис. 1 Пример циклической цепи
Рассмотрим, как инерционный закон функционирования автоматов позволяет рассматривать схемы с контурами обратной связи. Наличие подобных связей создает множество проблем, в том числе и в [параллельном] программировании, но они почему-то «исключаются из рассмотрения» теорией автоматов (см. правильные логические сети (ППЛС) в [15]).
Заметим, что требование единого времени относится только к автоматным объектам, составляющим единую модель. Она известна под именем синхронных сетей автоматов (ССА) [16]. Единое время также необходимо для создания и применимости операций композиции и декомпозиции автоматов, без которых сложно представить анализ и синтез автоматов. У независимых же моделей дискретное время может вполне различаться и каждая из них в общем случае может иметь свое дискретное время (см. понятие автоматных пространств в ВКПа). Но тогда перестают работать упомянутые алгебраические операции.
Заметим, что управление дискретным временем весьма удобно с практической точки зрения. Малое дискретное время можно назначать быстротекущим процессам, а большое — сервисным, диалогам и/или не столь критичным ко времени получения результата процессам. Такой подход может значительно уменьшить системные потери, связанные с переключением процессов. Особенно это критично в ситуации ограниченных вычислительных ресурсов.
4. Дизъюнктивная форма структурных конечных автоматов
Программирование предъявляет определенные требования к языку программирования или, что точнее, к вычислительной модели, которую он представляет. Поэтому, если стоит задача использовать автоматы в программировании, модель КА необходимо адаптировать. Весьма важно при этом сохранить эквивалентность классической модели автомата. Претензии к АП во многом сводятся к тому, что это важное условие нарушается. А это ведет уже к тому, что сложно или просто невозможно применить результаты классической теории в отношении к используемой программной модели.
Более того, существует даже мнение об ограниченности или даже невозможности использования автоматов для описания и моделирования систем параллельного типа, что прямо или косвенно становится аргументом в пользу других моделей. Примером может служить обоснования преимущества сетей Петри перед автоматами, приведенные в книге Дж. Питерсона (см. п.3.1.1 в [17]). Поэтому расширение возможностей автоматов имеет не только теоретическое, но большое практическое значение.
У обычной конечно-автоматной модели существуют также проблемы с компактным описанием процессов. Структурные автоматы, речь о которых пойдет далее, в сравнении с абстрактными автоматами имеют больше возможностей для описания процессов и отражения их взаимодействия. Они же позволяют получить более компактное описание, начиная с модели отдельного процесса, а также дополняют теорию анализа параллельных систем новыми возможностями анализа и синтеза.
В отличие от абстрактных автоматов, которые оперирую множествами входных и выходных символов, поступающих по единственному входному и выходному каналам, в структурных автоматах данные множества представлены структурными алфавитами, состоящими из элементарных конъюнкций логических переменных. При этом для каждой логической переменной создается свой входной/выходной канал. В этом случае мы на структурном уровне оперируем m, n-полюсником, который имеет уже m входных и n выходных каналов.
Рассматривая подобные структурные автоматы, будем допускать наличие у них «пустых» наборов для входных и выходных логических переменных. Они будут в этом случае представлены символом «прочерк». Переход, помеченный «пустым» входным набором — это безусловный переход в следующее состояние. Такой переход у состояния может быть один и только один. Использование прочерка на месте выходного набора будет соответствовать отсутствию выходных сигналов. Для программ это означает отсутствие каких-либо действий с памятью.
Введем по аналогии с нормальными формами булевых функций нормальную форму описания вполне определенных структурных автоматов. Это даст более компактное их представление, т.к. позволит в явной форме выделить подавтомат, несущий существенную информацию о функционировании автомата. Под существенной информацией понимается смена текущего состояния и/или выдача выходных сигналов даже без перехода в новое состояние. Напомним, что для дизъюнктивных форм булевых функций (БФ) аналогичный подход отделяет единичные значения булевой функции от ее нулевых значений, и нулевые значения функции от единичных для конъюнктивных форм БФ.
Определение 5. Назовем дизъюнктивной нормальной формой структурных конечных автоматов (ДНФ СКА) вполне определенные структурные автоматы, переходы которых помечены элементарными конъюнкциями логических переменных.
Пусть модель ДНФ СКА содержит только результативные переходы, т.е. переходы, помеченные выходными сигналами, или переходы с прочерком на месте выходных сигналов, но изменяющие текущее состояние автомата. Переходы, не включенные в нормальную форму автомата, представляют дополнение ДНФ СКА до вполне определенного автомата. По форме такому дополнению соответствует автомат, состоящий из изолированных состояний с переходами в виде петель с прочерками на месте выходных сигналов. Именно этот подавтомат, как далее будет показано, мы и можем исключить из описания автомата, тем самым минимизировав его.
Определение 6. Автоматы ДНФ СКА, переходы которых помечены конституентами единиц (элементарные конъюнкции ранга m для автомата, имеющего m входных каналов), назовем канонической или совершенной формой представления дизъюнктивных нормальных форм структурных автоматов — ДКФ СКА (СДНФ СКА).
Любой вполне определенный дизъюнктивный структурный автомат M можно представить объединением двух подавтоматов — подавтомата S, который является ДНФ СКА, и подавтомата ^S, состоящего из подмножества состояний автомата M с переходами в форме петель, где
. (4)
Когда все переходы у автомата результативные, имеем M = S.
Покажем на примерах способы задания структурных автоматов в форме ДНФ СКА.
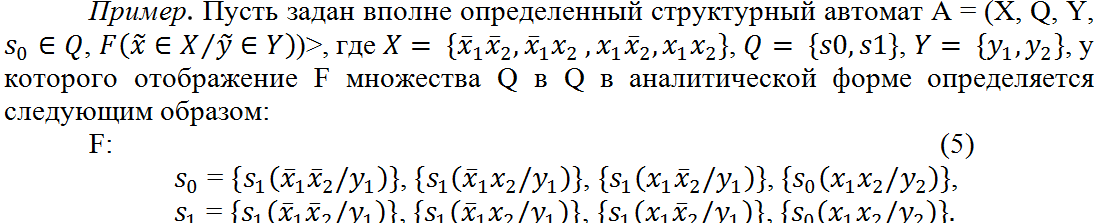
Далее будем использовать упрощенную форму текстового задания, заменяя символ «отрицания» символом ^ или ¬ (далее будем использовать ^). Так, например, элементарная конъюнкция будет записана как ^x1^x2. В этом случае отображение (5) примет следующий вид:
F: (6)
s0 = {s1(^x1^x2/y1), s1(^x1×2/y1), s1(x1^x2/y1), s0(x1×2/y2)},
s1 = {s1(^x1^x2/y1), s1(^x1×2/y1), s1(x1^x2/y1), s0(x1×2/y2)},
Когда выходным сигналам автомата удается поставить в соответствие внутренние состояния (по аналогии с автоматами Мура), то описание может быть дополнительно упрощено. В этом случае идет речь о смешанной модели автоматов Мили-Мура. Для приведенного выше примера состоянию s1 можно поставить в соответствие сигнал y1, а состоянию s0 — y2 и тогда отображение F будет следующим:
F: (7)
s0 = {s1(^x1^x2/-), s1(^x1×2/-), s1(x1^x2/-), s0(x1×2/-)},
s1 = {s1(^x1^x2/-), s1(^x1×2/-), s1(x1^x2/-), s0(x1×2/-)},
В приведенных примерах F является вполне определенным структурным автоматом. Но, начиная с формулы (7), уже можно выделить подавтоматы. Обозначим их F и ^F. В результате получим подавтоматы следующего вида:
F: (8)
s0 = {s1(^x1^x2/-), s1(^x1×2/-), s1(x1^x2/-)},
s1 = {s0(x1×2/-)},
^F: (9)
s0 = {s0(x1×2/-)},
s1 = {s1(^x1^x2/-), s1(^x1×2/-), s1(x1^x2/-)}.
В дальнейшем отображение M будем ассоциировать только с отображением F. Это вполне допустимо, т.к. по нему можно однозначно сначала восстановить отображение ^F и далее, объединив отображения, найти исходный вполне определенный автомат M.
Дизъюнктивные канонические формы структурных конечных автоматов после выполнения операций минимизации переходят в эквивалентные, но более компактные формы ДНФ СКА. Для этого необходимо выполнить минимизацию соответствующих ДКФ булевых функций, построенных из конституент единиц переходов, имеющих общие входное и выходное состояния и помеченных одинаковыми наборами выходных сигналов или символом прочерк.
Для рассматриваемого примера необходимо минимизировать следующую БФ (см. состояние s0):
y = ^x1^x2 ^x1×2 x1^x2 = ^x1 ^x2. (10)
После минимизации отображения F и ^F, представленные формулами (8) и (9), примут вид:
F: (11)
s0 = {s1(^x1/-), s1(^x2/-)},
s1 = {s0(x1×2/-)}.
^F: (12)
s0 = {s0(x1×2/-)},
s1 = {s1(^x1/-), s1(^x2/-)}.
По ДНФ СКА, выполняя действия обратные рассмотренной процедуре минимизации автомата, однозначно находится его каноническое представление — ДКФ СКА. Далее можно найти дополнение до вполне определенного автомата и, следовательно, восстановить исходное представление любого вполне определенного автомата.
5. Сети структурных автоматов
Синхронные сети из структурных автоматов (ССА) представляют адекватную параллельным процессам формальную модель[16]. При этом в качестве модели компонентного автомата сети может быть выбрана модель ДНФ СКА. Однако, если говорить об алгоритмической модели параллельных процессов, то ССА является лишь частью более общей модели параллельных процессов — параллельной алгоритмической машины. Последняя, кроме автоматного управления в форме ДНФ СКА или ССА на базе ДНФ СКА, включает дополнительно модели памяти и операторов (см. определение автоматной программы).
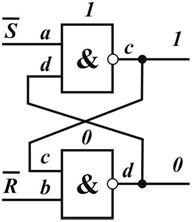Рис. 2. Схема RS-триггера на элементах И-НЕ
Учитывая, что ДНФ СКА, представленный формулой (11), представляет модель элемента И-НЕ, то модель асинхронного RS-триггера (рис. 2), состоящая из двух подобных автоматов, будет следующей:
S: (13)
s0 = {s1(^a/-), s1(^d/-)},
s1 = {s0(ad/-)}.
R:
w0 = {w1(^c/-), w1(^b/-)},
w1 = {w0(cb/-)}.
Здесь логическим переменным a, b, c, d (см. рис. 2) соответствуют входные сигналы, принадлежащие соответствующим компонентным автоматам сети. В этом случае они являются локальными переменными соответствующих структурных автоматов.
Введем логические переменные x1 и x2, соответствующие установочным входам RS-триггера, и свяжем внутренние состояния автоматных моделей элементов И-НЕ с состоянием его выходов. В результате модель RS-триггера (13) можно представить в следующем эквивалентном виде:
S: (14)
s1 = {s0(x1w1/-)},
s0 = {s1(^x1/-), s1(w0/-)}.
R:
w1 = {w0(s1×2/-)},
w0 = {w1(s0/-), w1(^x2/-)}.
Выше автоматы представлены аналитической формой описания. Она удобна для различных математических преобразований, но автоматные графы в определенной ситуации явно нагляднее. На рис. 3 показана эквивалентная аналитической форме двухкомпонентная параллельная графическая модель RS-триггера, дополненная связями в форме, позаимствованной у сетей Петри. На графе двойными кружками выделены начальные состояния автоматов сети, а пунктирные дуги отражают синхронизирующие связи, которым в аналитической форме будут соответствовать входные сигналы.
Рис. 3. Граф сетевой модели RS-триггера на элементах И-НЕ
Синхронизирующие связи связывают автоматы. При этом состояния одних являются источниками входных сигналов для других. Синхронизирующий входной сигнал будет true, если состояние автомата, с которым связан автомат, примет соответствующее значение, и false в случае любого другого значения состояния.
6. Операция умножения структурных автоматов
Параллельные системы характеризуются поведением, которое понять, порой, не просто. Любой [параллельный] программист знаком с этим не понаслышке. В случае автоматных процессов полное представление об алгоритме функционирования модели параллельного типа дает эквивалентный однокомпонентный автомат. Его при необходимости (что само по себе может быть не так уж просто) можно найти путем применения к сетевой модели алгебраической операции умножения автоматов.
Для автоматов в форме ДНФ СКА операция умножения, обозначаемая далее, определяется следующим образом (формулировку аналогичной операции для абстрактных автоматов см. в [11]). Пусть M — бесконечное множество структурных автоматов и — произвольные непустые автоматы в форме ДНФ СКА. Обозначим их через и , где — соответственно входные и выходные структурные алфавиты, — алфавиты состояний, а — отображения соответственно Q и W в себя. ДНФ СКА , обозначаемый , называется произведением автоматов , если
где, причем. Начальным состоянием автомата будет состояние. Поскольку вполне определенные автоматы, то и автомат K также является вполне определенным автоматом.
Исходя из определения ДНФ СКА, вычисление результирующего отображения R можно упростить, исключив операцию умножения дополнений автоматов. В результате получим:
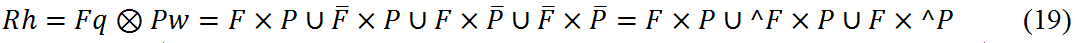
Еще больше упростить процедуру вычисления результирующего отображения можно, если использовать внутренние состояния автоматов. Продемонстрируем это на примере нахождения автомата эквивалентного сетевой модели RS-триггера (14).
С учетом дополнения (12) для каждого из компонентных автоматов, вычисление частичных сумм и отображения Rh (16) будет выглядеть следующим образом.
где дополнения ДНФ СКА R и S до вполне определенных автоматов будут следующими (см. также рис. 3):
^R: (21)
w0 = {w0(s1×2/-)},
w1 = {w1(s0/-), w1(^x2/-)}.
^S: (22)
s0 = {s0(x1w1/-)},
s1 = {s1(w0/-), s1(^x2/-)}.
Рассмотрим подробнее вычисление множества переходов для компонентных состояний {w0s0, w1s0, w0s1, w1s1} эквивалентного автомата подавтомата R: (см. также (14))
Для (26) входное x1w1s1×2 упрощено до x1×2, поскольку текущее компонентное состояние совпадает с именами логических переменных, включенных в условие перехода.
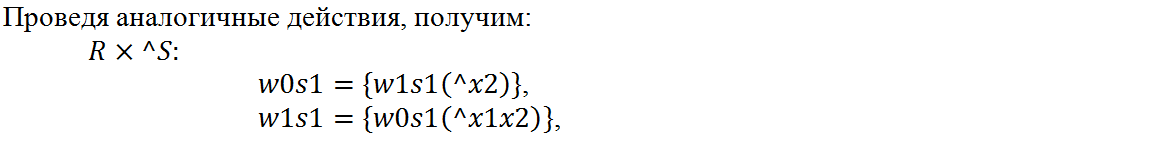
Рис. 4. Граф результирующего автомата сетевой модели RS-триггера
На графе нюансы функционирования RS-триггера совсем уж очевидны. Легко видеть, что переход из одного устойчивого состояние триггера в другое обязательно проходит через, так называемое, запрещенное состояние. Вероятен и совсем парадоксальный для триггера режим — генерация. В реальной жизни он невозможен, т.к. реальные элементы всегда отличаются друг от друга, как минимум, величиной задержек, а этому соответствует уже несколько иная модель (см. далее модели задержек).
7. Теневая модель памяти автоматных программ
Для корректной реализации параллелизма программам необходима модель памяти типа CREW (concurrent read exclusive — write) [18], в которой чтение разрешено любым параллельным операторам, а изменение общих данных — только одному из них. Автоматная модель управления ограничивает исполнение операторов программы границами текущего дискретного такта. В такой ситуации изменение памяти со стороны действий могут фиксироваться в «теневой памяти», чтобы после их завершения стать ее новыми значениями.
Подобное взаимодействие операторов с памятью будем называть теневой моделью памяти. Она является важной частью модели памяти АП, обеспечивая корректность параллельных вычислений. Введение модели памяти упрощает программирование, т.к. становятся во многом не нужными, прямо скажем, не очень надежные механизмы синхронизации процессов (подробнее см. [19]).
Но автоматное программирование в силу эквивалентности автоматов и граф-схем алгоритмов (ГСА) (см. [20]) не запрещает использовать и любые другие механизмы управления параллельными вычислениями. Но ответственность за результат в этом случае будет нести уже программист [19].
8. Вложенная и инерционная модели автоматов
Без подпрограмм, создающих вложенную иерархию в программировании, программирование немыслимо. Но теория автоматов фактически игнорирует вложенные автоматы [21]. Рассмотрим пример, демонстрирующий, с одной стороны, сложность автоматного проектирования на базе обычной модели, а, с другой стороны, его простоту в рамках иерархической модели. Введенная модель вложенных автоматов порождает подкласс автоматов, названный далее инерционными автоматами, и соответствующий ему подкласс инерционных алгоритмов.
Итак, пусть стоит задача создания модели элемента задержки, реализующего без преобразования передачу двоичного сигнала. Пусть при этом времена задержек t01и t10, определяющие задержки переключения элемента в единичное и нулевое состояния, в общем случае не совпадают.
Модель простейшей единичной задержки автомата Мили показана на рис. 5 (ср. с моделью задержки в [21]). Более сложную модель транспортной задержки (о типах задержек подробнее см. [22]) в форме автомата Мили и совмещенной модели Мили-Мура демонстрируют рис. 6а и рис. 6 б.
Рис. 5. Модель единичной задержки в форме автомата Мили
Рис. 6. Модель транспортной задержки Мили (а) и Мили-Мура (б)
У моделей сигнал x3 примет истинное значение при равенстве значения счетчика тактов переменной t (не путать с дискретным временем модели) со значением t01или t10. Переменной t значение присваивается сигналами y4 или y3. Сигналы y1, y2 присваивают значение выходу модели, а сигнал y5 увеличивает счетчик тактов, который сбрасывается сигналом y6.
Модели на рис. 6 демонстрируют отличие автоматов Мили от автоматов Мура. Модель Мили считается удобнее, но модель Мура в определенном смысле надежнее. В нашем случае она точнее инициирует счетчик тактов, установку выходного значения и подсчет тактов, т.к. исключает повтор сигналов на переходах в состояния »0» и »1».
Механизм вложения автоматов формирует технологию модульного проектирования программ. При этом реализовать программное вложение автоматов много проще, чем аппаратное (см. [23]). Для этого
