Arend – язык с зависимыми типами, основанный на HoTT (часть 1)
В данном посте мы поговорим о только что выпущенном JetBrains языке с зависимыми типами Arend. Этот язык разрабатывался JetBrains Research на протяжении последних нескольких лет. И хотя репозитории уже год назад были выложены в открытый доступ на github.com/JetBrains, полноценный релиз Arend случился лишь в июле этого года.
Мы попробуем рассказать, чем Arend отличается от существующих систем формализованной математики, основанных на зависимых типах, и о том, какая функциональность уже сейчас доступна его пользователям. Мы предполагаем, что читатель настоящей статьи в целом знаком с зависимыми типами и слышал хотя бы про один из языков, основанных на зависимых типах: Agda, Idris, Coq или Lean. При этом мы не рассчитываем, что читатель владеет зависимыми типами на продвинутом уровне.
Для простоты и конкретности наш рассказ об Arend и гомотопических типах будет сопровождаться реализацией на Arend простейшего алгоритма сортировки списков — даже на этом примере можно почувствовать отличие Arend от Agda и Coq. На Хабре уже есть ряд статей, посвященных зависимым типам. Скажем, про реализацию сортировки списков методом QuickSort на Agda есть вот такая статья. Мы будем реализовывать более простой алгоритм сортировки вставками. При этом основное внимание уделим конструкциям языка Arend, а не самому алгоритму сортировки.
Читать статью
Итак, основным отличием Arend от других языков с зависимыми типами является логическая теория, на которой он основан. В Arend в качестве таковой используется открытая недавно В. Воеводским гомотопическая теория типов (HoTT). Если точнее, то Arend основан на разновидности HoTT под названием «теория типов с интервалом». Напомним, что Coq основан на так называемом исчислении индуктивных конструкций (Calculus of Inductive Constructions), а Agda и Idris — на интенциональной теории типов Мартин-Лёфа. Тот факт, что Arend основан на HoTT, существенно влияет на его синтаксические конструкции и работу алгоритма проверки типов (тайпчекера). Эти особенности мы и собираемся обсудить в настоящей статье.
Попробуем ещё коротко описать состояние инфраструктуры языка. Для Arend существует плагин для IntelliJ IDEA, который можно установить прямо из репозитория IDEA-плагинов. В принципе, установки плагина достаточно для полноценной работы с Arend, скачивать и устанавливать что-нибудь ещё не требуется. Помимо проверки типов, Arend-плагин предоставляет привычную для пользователей IDEA функциональность: имеется подсветка и выравнивание кода, различные рефакторинги и подсказки. Существует также возможность использования консольной версии Arend. Более подробное описание процесса установки можно найти здесь.
Примеры кода, приведенные в настоящей статье, основаны на стандартной библиотеке Arend, поэтому мы рекомендуем скачать ее исходный код из репозитория. После скачивания директорию с исходным кодом нужно импортировать как IDEA-проект при помощи команды Import Project. На Arend уже удалось формализовать некоторые разделы гомотопической теории типов и теории колец. Например, в стандартной библиотеке присутствует реализация кольца рациональных чисел Q вместе с доказательствами всех требуемых теоретико-кольцевых свойств.
Подробная документация к языку, в которой многие моменты, затрагиваемые в настоящей статье, объяснены более развернуто, также находится в открытом доступе. Напрямую задавать вопросы разработчикам Arend можно в телеграм-канале.
1. Краткий обзор HoTT/Arend
Гомотопическая теория типов (или коротко HoTT) — это разновидность интенциональной теории типов, отличающаяся от классической теории типов Мартин-Лёфа (MLTT, на которой основана Agda) и исчисления индуктивных конструкций (CIC, на котором основан Coq) тем, что в ней наряду с утверждениями и множествами присутствуют так называемые типы более высокого гомотопического уровня.
В данной статье мы не ставим себе цели в деталях объяснить основания HoTT — для подробного изложение этой теории потребовалось бы пересказать целую книгу (см. этот пост). Отметим лишь, что теория, основанная на аксиоматике HoTT, получается в некотором смысле гораздо элегантнее и интереснее классической теории типов Мартин-Лёфа. Так, ряд аксиом, которые раньше приходилось дополнительно постулировать (например, функциональная экстенсиональность), доказываются в HoTT как теоремы. Кроме того, в HoTT можно внутренним образом определить многомерные гомотопические сферы и даже посчитать некоторые их группы гомотопий.
Однако эти аспекты HoTT интересны в первую очередь математикам, а цель данной статьи — объяснить, чем основанный на HoTT Arend выгодно отличается от Agda/MLTT и Coq/CIC на примере представления таких простых и привычных любому программисту сущностей, как упорядоченные списки. При чтении этой статьи достаточно относиться к HoTT как к разновидности интенциональной теории типов с более развитой аксиоматикой, дающей удобства при работе с вселенными и равенствами.
1.1 Зависимые типы, соответствие Карри — Ховарда, вселенные
Напомним, что языки с зависимыми типами отличаются от обычных функциональных языков программирования тем, что в них помимо привычных типов данных, таких как списки или натуральные числа, присутствуют типы, зависящие от значения параметра. Простейшими примерами таких типов являются векторы заданной длины n или сбалансированные деревья заданной глубины d. Несколько дальнейших примеров таких типов упомянуто здесь.
Напомним, что соответствие Карри — Ховарда позволяет интерпретировать утверждения логики как зависимые типы. Основная идея этого соответствия заключается в том, что пустой тип соответствует ложному утверждению, а населенные типы соответствуют истинному утверждению. Об элементах типа можно думать как о доказательствах соответствующего логического утверждения. Например, о любом элементе типа целых чисел можно думать как о доказательстве того факта, что целые числа существуют (то есть тип целых чисел населен).
Различные естественные конструкции над типами соответствуют различным логическим связкам:
- Произведение типов A × B, иногда называется типом пары Pair A B. Так как этот тип населен тогда и только тогда, когда оба типа A и B населены, то эта конструкция соответствует логическому «и».
- Сумма типов A + B. В Haskell этот тип называется Either A B. Так как этот тип населен тогда и только тогда, когда один из типов A или B населен, то эта конструкция соответствует логическому «или».
- Функциональный тип A→B. Любая функция такого типа преобразует элементы A в элементы B. Таким образом, такая функция существует в точности тогда, когда существование элемента типа A влечет существование элемента типа B. Следовательно, эта конструкция соответствует импликации.
Пусть теперь дан некоторый тип A и семейство типов B, параметризованное элементом a типа A. Приведем примеры более сложных конструкций над зависимыми типами.
- Зависимый функциональный тип Π(a: A) (B a). Данный тип совпадает с привычным функциональным типом A → B в случае, если B не зависит от A. Функция типа Π(a: A) (B a) преобразует любой элемент a типа A в элемент типа B a. Таким образом, такая функция существует тогда и только тогда, когда для любого a : A существует элемент B a. Следовательно, эта конструкция соответствует квантору всеобщности ∀. Для зависимого функционального типа в Arend используется синтаксис
\Pi (x : A) -> B a, а населяющий данный тип терм можно построить при помощи лямбда-выражения\lam (a : A) => f a. - Тип зависимых пар Σ(a: A) (B a). Данный тип совпадает с привычным типов пар A×B, если B не зависит от A. Тип Σ(a: A) (B a) населен в точности когда существует некоторый элемент a: A и элемент типа B a. Таким образом, этот тип соответствует квантору существования
∃. Тип зависимых пар в Arend обозначается\Sigma (a : A) (B a), а населяющие его термы строятся при помощи конструктора (зависимой) пары(a, b). - Тип равенства a = a», где a и a» — два элемента некоторого типа A. Такой тип населен, если a и a» равны, и пуст иначе. Очевидно, этот тип является аналогом предиката равенства в логике.
В этом месте мы отсылаем читателя к источникам, в которых соответствие Карри — Ховарда разбирается более подробно (см., например, курс лекций или статьи здесь или здесь).
Все выражения, рассматриваемые в теории типов, должны обладать некоторым типом. Так как выражения, обозначающие типы, также рассматриваются в рамках данной теории, им тоже необходимо присвоить некоторый тип. Возникает вопрос, что это должен быть за тип?
Первое наивное решение, которое приходит в голову, — приписать всем типам некоторый формальный тип \Type, называемый вселенной (он так называется, потому что содержит вообще все типы). Если мы воспользуемся этой вселенной, то упомянутые выше конструкции суммы и произведения типов получат сигнатуру \Type → \Type → \Type, а более сложные конструкции зависимого произведения и зависимой суммы — сигнатуру Π (A : \Type) → ((A → \Type) → \Type).
В этот момент возникает вопрос, какой тип должна иметь сама вселенная \Type? Наивная попытка сказать, что типом вселенной \Type, по определению, является сама \Type приводит к парадоксу Жирара, поэтому вместо одной вселенной \Type рассматривают бесконечную иерархию вселенных, т.е. вложенную цепочку вселенных \Type 1 < \Type 2 < …, уровни которых занумерованы натуральными числами, а типом вселенной \Type i, по определению, является вселенная \Type (i+1). Для упомянутых выше конструкций типов также приходится вводить более сложные сигнатуры.
Таким образом, вселенные в теории типов нужны для того, чтобы любое выражение обладало некоторым типом. В некоторых разновидностях теории типов вселенные используются и с другой целью: для различения между разновидностями типов. Мы уже видели, что частными случаями типов являются множества и утверждения. Это показывает, что, возможно, имело бы смысл ввести в теорию отдельную вселенную Prop для утверждений и отдельную иерархию вселенных Seti для множеств. Именно такой подход применяется в Calculus of Inductive Constructions — теории, на которой основана система Coq.
1.2 Примеры простейших индуктивных типов и рекурсивных функций
Рассмотрим определения на Arend простейших индуктивных типов данных: булева типа, типа натуральных чисел и полиморфных списков. Для введения новых индуктивных типов в Arend используется ключевое слово \data.
\data Empty -- Пустой тип, не имеющий конструкторов
\data Bool
| true
| false
\data Nat
| zero
| suc Nat
\data List (A: \Set)
| nil
| \infixr 5:-: A (List A)
Как видно из примеров выше, после ключевого слова \data требуется указать имя индуктивного типа и список его конструкторов. И тип данных, и конструкторы при этом могут обладать некоторыми параметрами. Скажем, в примере выше тип List обладает одним параметром A. Конструктор списка nil не имеет параметров, а конструктор :-: имеет два параметра (один из которых имеет тип A, а другой — List A). Вселенная \Set состоит из типов, являющихся множествами (определение множеств будет дано в следующем разделе). Ключевое слово \infixr позволяет использовать инфиксную нотацию для конструктора :-: и, кроме того, сообщает парсеру Arend, что оператор :-: является правоассоциативной операцией с приоритетом 5.
В Arend все ключевые слова начинаются с символа обратной косой черты (»\»), такая реализация вдохновлена LaTeX. Сразу отметим, что лексические правила в Arend весьма либеральны: Circle_HSpace, contrFibers=>Equiv, suc/=0, zro_*-left и даже n:Nat — все эти литералы являются примерами корректных идентификаторов в Arend. Последний пример показывает, насколько важно пользователю Arend не забывать ставить пробелы между идентификаторами и символами двоеточия. Отметим, что в идентификаторах Arend не разрешается использовать символы Unicode (в частности, нельзя использовать кириллицу).
Для определения функций в Arend используется ключевое слово \func. Синтаксис этой конструкции устроен так: после ключевого слова \func нужно указать имя функции, её параметры и тип возвращаемого значения. Последний элемент определения функции — ее тело.
Если возможно явно указать выражение, в которое данная функция должна вычисляться, то, для того чтобы указать тело функции, используется лексема =>. Рассмотрим, например, определение функции отрицания типа.
\func Not (A : \Type) : \Type => A -> Empty
Тип возвращаемого значения у функции не всегда обязательно указывать явно. В примере выше Arend сумел бы самостоятельно вывести тип Not, а мы могли бы опустить выражение »: \Type» после скобок.
Как и в большинстве систем формализованной математики, пользователю не обязательно указывать явный предикативный уровень у вселенной \Type, а определения, в которых вселенные используются без явного указания предикативного уровня, считаются по нему полиморфными.
Попробуем теперь определить функцию, вычисляющую длину списка. Такую функцию легко определить через сопоставление с образцом (pattern matching). В Arend для этого используется ключевое слово \elim. После него необходимо указать переменные, по которым производится сопоставление (если таких переменных больше одной, то их следует писать через запятую). Если сопоставление производится по всем явным параметрам, то \elim вместе с переменными можно опустить. Далее следует блок пунктов сопоставления, отделенных друг от друга вертикальной чертой »|». Каждый пункт в этом блоке представляет собой выражение вида «образцы, сопоставления записанные через запятую» => «выражение».
\func length {A : \Set} (l : List A) : Nat
| nil => 0
| :-: x xs => suc (length xs)
В примере выше параметр A функции length окружен фигурными скобками. Эти скобки в Arend используются для обозначения неявных аргументов, т.е. аргументов, которые пользователь может опустить при вызове функции или использовании типа. Отметим, что в Arend нельзя использовать инфиксную нотацию для обозначения конструкторов при сопоставлении с образцом, поэтому в примере для образцов используется префиксная нотация.
Как и в Coq/Agda, в Arend все функции должны гарантированно завершаться (т.е. в Arend присутствует termination checking). В определении функции length данная проверка проходит успешно, поскольку при рекурсивном вызове происходит строгое уменьшение первого явного аргумента. Если бы такого уменьшения не происходило, то Arend выдал бы сообщение об ошибке.
\func bad : Nat => bad
[ERROR] Termination check failed for function 'bad'
In: bad
В Arend разрешены круговые зависимости и взаимно рекурсивные функции, для которых также выполняется проверка на завершение. Алгоритм этой проверки реализован по мотивам статьи А. Абеля. В ней вы найдете более подробное описание условий, которым должны удовлетворять взаимно рекурсивные функции.
1.3 Чем множества отличаются от утверждений?
Ранее мы уже писали, что примерами типов являются множества и утверждения. Кроме того, мы использовали ключевые слова \Type и \Set для обозначения вселенных в Arend. В этом разделе мы попробуем подробнее объяснить, чем утверждения отличаются от множеств с точки зрения разновидностей интенциональной теории типов (MLTT, CIC, HoTT), а заодно объяснить, в чём состоит смысл ключевых слов \Prop, \Set и \Type в Arend.
Напомним, что в классической теории Мартин-Лёфа нет разделения типов на множества и утверждения. В частности, в теории есть только одна кумулятивная вселенная (которая обозначается либо Set в Agda, либо Type в Idris, либо Sort в Lean). Данный подход наиболее прост, однако существуют ситуации, в которых проявляются его недостатки. Допустим, мы пытаемся реализовать тип «упорядоченный список» как зависимую пару, состоящую из списка и доказательства его упорядоченности. Оказывается, что тогда в рамках «чистой» MLTT не получится доказать равенство упорядоченных списков, состоящих из одинаковых элементов, у которых при этом различаются термы-доказательства упорядоченности. Иметь такое равенство было бы весьма естественно и желательно, так что невозможность его доказать можно рассматривать как теоретический изъян MLTT.
В Agda данная проблема частично решается при помощи так называемых аннотаций несущественности (см. источник, в котором пример со списком разбирается более подробно). Эти аннотации, однако, не являются конструкцией из теории MLTT, также они не являются полноценными конструкциями над типами (невозможно пометить такой аннотацией тип, используемый не в аргументе функции).
В Coq, основанном на CIC, есть две различные вложенные друг в друга вселенные: Prop (вселенная утверждений) и Set (вселенная множеств), которые погружены в объемлющую иерархию вселенных Type. Основное отличие между Prop и Set состоит в том, что на переменные, тип которых принадлежит Prop, в Coq накладывается ряд ограничений. Например, их нельзя использовать в вычислениях, а сопоставление с образцом для них возможно лишь внутри доказательств других утверждений. С другой стороны, все элементы типа, принадлежащего вселенной Prop, равны по аксиоме несущественности доказательств, см. формулировку в Coq.Logic.ProofIrrelevance. При помощи этой аксиомы мы легко смогли бы доказать равенство упомянутых выше упорядоченных списков.
Рассмотрим, наконец, подход Arend/HoTT к утверждениям и вселенным. Основное отличие состоит в том, что HoTT обходится без аксиомы несущественности доказательств. То есть в HoTT нет специальной аксиомы, постулирующей, что все элементы утверждений равны. Зато в HoTT, тип, по определению, является утверждением, если можно доказать, что все его элементы равны друг другу. Мы можем определить предикат на типах, который верен, если тип является утверждением:
\func isProp (A : \Type) => \Pi (a a' : A) -> a = a'
Возникает вопрос: какие типы удовлетворяют этому предикату, то есть являются утверждениями? Легко убедиться, что это верно для пустого и одноэлементного типов. Для типов, где есть по крайней мере два различных элемента, это уже не будет верно.
Разумеется, мы хотим, чтобы над утверждениями были определены все необходимые логические связки. В разделе 1.1 мы уже обсуждали, как их можно было бы определить при помощи теоретико-типовых конструкций. Имеется, однако, следующая проблема: не все введенные нами операции сохраняют свойство isProp. Конструкции произведения типов и (зависимого) функционального типа сохраняют это свойство, в то время как конструкции суммы типов и зависимых пар — нет. Таким образом, мы не можем использовать дизъюнкцию и квантор существования.
Данную проблему можно решить при помощи новой конструкции, которая добавляется в HoTT, так называемого пропозиционального усечения (propositional truncation). Эта конструкция позволяет превратить любой тип в утверждение. Её можно рассматривать как формальную операцию, делающую равными все термы, населяющие данный тип. Данная операция чем-то сходна с аннотациями несущественности из Agda, однако, в отличие от них, является полноценной операцией над типами с сигнатурой \Type -> \Prop.
Последний важный пример утверждений — это равенство двух элементов некоторого типа. Оказывается, что в общем случае тип равенства a = a' не обязан быть утверждением. Типы, для которых он является таковым, называются множествами:
\func isSet (A : \Type) => \Pi (a a' : A) -> isProp (a = a')
Все типы, которые встречаются в обычных языках программирования, удовлетворяют этому предикату, то есть равенство на них является утверждением. Например, это верно для натуральных чисел, целых чисел, произведений множеств, сумм множеств, функций над множествами, списков множеств и других индуктивных типов данных, сконструированных из множеств. Это означает, что если нас интересуют только такие привычные конструкции, то мы можем не задумываться о произвольных типах, которые не удовлетворяют этому предикату. Все типы, встречающиеся в Coq, являются множествами.
Типы, не являющиеся множествами, становятся полезны, если хочется заниматься гомотопической теорией типов. Пока что мы просто отошлем читателя к модулю стандартной библиотеки, содержащему определение n-мерной сферы, — примеру типа, не являющегося множеством.
В Arend имеются специальные вселенные \Prop и \Set, состоящие из утверждений и множеств, соответственно. Если мы уже знаем, что тип A содержится во вселенной \Prop (или \Set), то тогда доказательство соответствующего свойства isProp (или isSet) в Arend может быть получено при помощи встроенной в прелюдию аксиомы Path.inProp (мы приведем пример использования этой аксиомы в разделе 2.3).
\func inProp {A : \Prop} : \Pi (a a' : A) -> a = a'
Мы уже отмечали, что не все естественные конструкции над типами сохраняют свойство isProp. Например, индуктивные типы данных с двумя и более конструкторами никогда не удовлетворяют ему. Как было отмечено выше, мы можем воспользоваться конструкцией пропозиционального усечения, превращающей любой тип в утверждение.
В библиотеке Arend стандартная реализация пропозиционального усечения называется Logic.TruncP. Мы могли бы определить тип логического «или» в Arend как усечение суммы типов:
\data \fixr 2 Or (A B : \Type) -- Sum of types; analogue of Coq's type "sum"
| inl A
| inr B
\func \infixr 2 || (A B: \Type) => TruncP (sum A B) — Logical «or», analogue of Coq’s type »\/»
В Arend существует и другой, более простой и удобный способ определить пропозиционально усеченный индуктивный тип. Для этого достаточно добавить ключевое слово \truncated перед определением типа данных. Например, определение логического «или» в стандартной библиотеке Arend дается следующим образом.
\truncated \data \infixr 2 || (A B : \Type) : \Prop -- Logical "or”, analogue of Coq's type "\/"
| byLeft A
| byRight B
Дальнейшая работа с пропозиционально усеченными типами напоминает таковую с типами, отнесенными ко вселенной Prop в Coq. Например, сопоставление с образцом переменной, тип которой является утверждением, разрешено только в ситуации, когда тип определяемого выражения сам является утверждением. Таким образом, всегда легко определить функцию Or-to-|| через сопоставление с образцом, но обратную к ней функцию —только в случае, если тип A `Or` B является утверждением (что бывает достаточно редко, например, когда типы A и B оба являются утверждениями и взаимно исключают друг друга).
\func Or-to-|| {A B : \Prop} (a-or-b : A `Or` B) : A || B
| inl a => byLeft a
| inr b => byRight
Вспомним также, что особенность механизма вселенных в Coq в том, что если какое-то определение было отнесено ко вселенной Prop, то уже никаким образом не получится использовать его при вычислении. По этой причине, сами разработчики Coq не рекомендуют использовать пропозициональные конструкции, а советуют по возможности заменять их на аналоги из вселенной множеств. Механизм вселенных Arend не имеет данного недостатка, то есть в определенных ситуациях оказывается возможным использовать утверждения в вычислениях. Мы приведем пример такой ситуации, когда будем обсуждать реализацию алгоритма сортировки списков.
1.4 Классы в Arend
Так как наша цель состоит в реализации простейшего алгоритма сортировки, кажется полезным перед этим ознакомиться с имеющейся в стандартной библиотеки Arend реализацией упорядоченных множеств.
В Arend классы используются для того, чтобы инкапсулировать операции и аксиомы, определяющие математические структуры, а также для того, чтобы выделять взаимосвязи между этими структурами при помощи наследования. Также классы являются пространствами имен, внутрь которых удобно помещать подходящие по смыслу конструкции и теории.
Базовым классом, от которого унаследованы все классы порядков в Arend, является класс BaseSet, не содержащий никаких членов помимо обозначения E для множества-носителя (т.е. множества на котором классы-потомки BaseSet уже вводят различные операции). Рассмотрим определение этого класса из стандартной библиотеки Arend.
\class BaseSet (E : \Set) -- определение, заимствованное из стандартной библиотеки
В определении выше носитель E объявляется параметром класса. Можно спросить, отличается ли чем-то приведенное выше определение BaseSet от следующего определения, в котором носитель E определен как поле класса?
\class BaseSet’ -- определение не из стандартной библиотеки
| E : \Set
Немного неожиданный ответ заключается в том, что в Arend нет разницы между этими двумя вариантами определения в том смысле, что любой параметр класса (даже неявный) в Arend, на самом деле, является его полем. Таким образом, для обоих вариантов реализации BaseSet, можно было бы использовать выражение x.E для доступа к полю E. Отличие между приведенными вариантами определения BaseSet всё же есть, но оно более тонкое, мы рассмотрим его подробнее в следующем разделе, когда будем обсуждать экземпляры классов (class instances).
Операция сортировки списка имеет смысл только в случае, когда на типе объектов списка задан линейный порядок, поэтому рассмотрим сначала определения строгого частично упорядоченного множества и линейно упорядоченного множества.
\class StrictPoset \extends BaseSet {
| \infix 4 < : E -> E -> \Prop
| <-irreflexive (x : E) : Not (x < x)
| <-transitive (x y z : E) : x < y -> y < z -> x < z
}
\class LinearOrder \extends StrictPoset {
| <-comparison (x y z : E) : x < z -> x < y || y < z
| <-connectedness (x y : E) : Not (x < y) -> Not (y < x) -> x = y
}
С точки зрения теории типов, классы в Arend можно рассматривать как аналоги сигма-типов с более удобным синтаксисом для проекций и конструкторов. Более точно, любой Arend-класс можно рассматривать как сигма-тип, компонентами которого являются все нереализованные поля класса.
Если тип поля является утверждением, то такое поле называется свойством. Свойства отличаются от полей тем, что их реализации никогда не вычисляются. Например, в StrictPoset поля <-irreflexive и <-transitive являются свойствами, а поля E и < — нет. Свойства дают заметный прирост производительности, так как их реализации (которые, по сути, являются доказательствами этих свойств) часто имеют большой размер, но вычислять их обычно не имеет смысла.
Для реализации алгоритма сортировки недостаточно иметь упорядоченное множество, необходимо еще знать, что этот порядок разрешим. Дело в том, что в Arend используется конструктивная математика, а значит, не все предикаты в нем разрешимы. В частности, равенство элементов разрешимо не для любого типа. Например, это верно для целых чисел, но не для множества функций над целыми числами, так как невозможно алгоритмически определить, равны ли две функции или нет. Мы можем определить класс множеств с разрешимым равенством следующим образом:
\class DecSet \extends BaseSet
| decideEq (x y : E) : Dec (x = y)
Предикат Dec определен над утверждениями таким образом, что Dec E верно тогда и только тогда, когда E разрешимо, то есть когда верно либо E, либо отрицание E.
\data Dec (E : \Prop)
| yes E
| no (Not E)
Рассмотрим, наконец, класс Dec (от слова decidable) из модуля Order.LinearOrder. Класс Dec реализует разрешимые линейные порядки, и, в частности, содержит нужную нам аксиому trichotomy, означающую, что любые два элемента типа E, сравнимы относительно порядка <. Таким образом, Dec можно рассматривать как аналог интерфейса Comparable из Java.
\class Dec \extends LinearOrder, DecSet {
| trichotomy (x y : E) : (x = y) || (x < y) || (y < x)
| <-comparison x y z x
| <-connectedness x y x/
| decideEq x y => {?}
}
Название класса Dec совпадает с названием уже введенного выше типа данных Dec, однако кажущегося конфликта обозначений, на самом деле, не возникает, так как в стандартной библиотеке этот класс содержится в другом пространстве имен. Мы же будем использовать Dec именно для обозначения класса, а не одноименного типа данных.
Аксиомы линейного порядка вытекают из аксиомы трихотомии, поэтому логично сразу же проверить эти аксиомы внутри класса Dec (в листинге выше мы для краткости опустили эти доказательства). Пример Dec показывает, что в Arend разрешено множественное наследование (Dec одновременно является потомком и LinearOrder, и DecSet), более того, разрешено даже ромбовидное наследование (diamond inheritance).
Для ромбовидного наследования имеется следующее естественное ограничение: одно и то же поле может быть реализовано в двух различных предках только в том случае, если эти реализации совпадают (либо если поле является свойством, так как реализация в этом случае игнорируется).
Если выбрать класс Dec в модуле Order.LinearOrder и попросить IDEA показать иерархию классов (обычно это делается при помощи нажатия [Ctrl]+[H]), то получится дерево, похожее на картинку ниже.
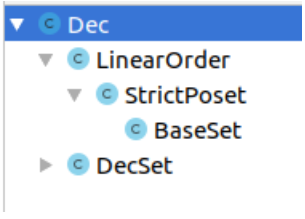
В этом месте мы предлагаем вам самостоятельно изучить полную иерархию классов стандартной библиотеки Arend (для этого достаточно попросить IDEA показать все подтипы BaseSet). Как можно заметить, иерархия эта уже сейчас весьма обширна.
1.5 Экземпляры классов, приведение типов, классифицирующие поля и перегрузка операторов.
Попробуем теперь создать экземпляр класса строгого порядка StrictPoset для типа натуральных чисел Nat. В Arend создать экземпляр класса можно только у классов, у которых реализованы все поля. Если следовать аналогии между классами и сигма-типами, то класс, все поля которого реализованы, соответствует пустому сигма-типу (то есть одноэлементному типу), а создание экземпляра класса соответствует взятию единственного значения этого одноэлементного типа.
Начнем с определения порядка и доказательств его простейших свойств: антирефлексивности и транзитивности. Оба этих свойства достаточно легко доказываются по индукции при помощи сопоставления с образцом.
data \infix 4 < (a b : Nat) \with
| zero, suc _ => zero
\lemma irreflexivity (x: Nat) (p: x < x) : Empty \lemma transitivity (x y z: Nat) (p: x < y) (q : y < z) : x < z В примерах выше вместо ключевого слова В примере выше Теперь мы можем создать экземпляр (instance) класса Выражение Мы уже отмечали выше, что поля классов ничем не отличаются от параметров классов. В частности, с точки зрения внутреннего представления выражение Альтернативный способ определить экземпляр класса Рассмотрим, наконец, ещё один способ определения экземпляра класса через ключевое слово В Arend реализован алгоритм поиска экземпляров классов, аналогичный таковому в языке Haskell. Реализация функции Напомним, что в реализации Мы упоминали, что параметры классов с точки зрения внутренней реализации Arend ничем не отличаются от полей классов. Однако в Arend имеется соглашение, что первый явный аргумент класса по умолчанию конвертируется не в обычное поле, а в так называемое классифицирующее поле (это соглашение работает, если »классифицирующее поле» не выбрано пользователем явно при помощи ключевого слова
| suc a, suc
| zero, suc y', suc z', zero\func мы использовали \lemma. Леммы относятся к функциям так же, как свойства классов относятся к полям классов, то есть выражения для них никогда не вычисляются, и это даёт прирост производительности. Как и в случае свойств классов, ключевое слово \lemma можно использовать, только если тип результата функции принадлежит вселенной \Prop.x'x' < y'. Мы будем и дальше использовать подобные названия для переменных-образцов (т.е. названия, которые совпадают с записью без пробелов утверждений, доказательством которых эти переменные являются). StrictPoset. В Arend для этого есть несколько различных вариантов синтаксиса. Первый способ создания экземпляра класса состоит в использовании ключевого слова \new внутри любого выражения. В этом случае будет создан «анонимный экземпляр класса».\func NatOrder => \new StrictPoset {
| E => Nat
| < => <
| <-irreflexive => irreflexivity
| <-transitive => transitivity
}StrictPoset { … } имеет смысл и без ключевого слова \new: в этом случае оно обозначает анонимный класс-расширение StrictPoset. В анонимных классах-расширениях необязательно реализовывать все поля, однако, как было сказано выше, применить к не полностью реализованному классу операцию \new не получится. Выражение вида \new C { … } имеет тип C { … }. Так как этот тип является наследником C, то оно также имеет тип C. Соответственно, в примере выше верно, что NatOrder является экземпляром класса StrictPoset.StrictPoset Nat ничем не отличается от выражения StrictPoset { | E => Nat }. Заметим, что мы могли бы указать тип функции NatOrder как StrictPoset, и это не считалось бы ошибкой благодаря привычным правилам подтипирования (наследник класса может использоваться вместо родителя).NatOrder заключается в использовании ключевого слова \cowith в заголовке функции (при этом тип функции обязательно должен быть указан и являться каким-то классом).\func NatOrder : StrictPoset \cowith {
| E => Nat
| < => <
| <-irreflexive => irreflexivity
| <-transitive => transitivity
}\instance. \instance NatOrder : StrictPoset {
| E => Nat
| < => <
| <-irreflexive => irreflexivity
| <-transitive => transitivity
}NatOrder через ключевое слово \instance аналогична реализации через \cowith и отличается от неё только тем, что эта функция будет использоваться во время поиска экземпляров класса StrictPoset (мы обсудим экземпляры чуть ниже).BaseSet из стандартной библиотеки множество-носитель E определяется как параметр класса (а не как поле), и мы в прошлом разделе сказали, что такая реализация обладает некоторым отличием от реализации E как поля класса. Сейчас мы прокомментируем это отличие подробнее. \classifying \field, у класса в Arend может быть только одно классифицирующее поле). Классифицирующие поля классов имеют следующие свойства: X имеет тип StrictPoset, то выражение List X полностью корректно и совпадает по значению с выражением List X.E.
