Анализ временных рядов, или как предсказать погоду на завтра05.08.2023 16:01

Введение

статья подготовлена UltraGeoPro

В данной статье будут рассмотрены способы анализа временных рядов и применение их на практике. Разберем основные методы прогнозирования упорядоченных данных.

Простыми словами, временной ряд — это данные, упорядоченные по времени (например, курс доллара).
Анализ временных рядов позволяет находить основные закономерности в данных и прогнозировать их.

Пример временного ряда (зависимость продаж от времени)

На текущий момент было изобретено большое кол-во методов работы со структурированными данными, так что мы рассмотрим лишь некоторые из них на примере данных о погоде с 2013 года по 2017.

Обработка данных

Для анализа временных рядов и их прогнозирования будет использован язык Python в связке со сторонними библиотеками (pandas, numpy, tensorflow, matplotlib). Статья содержит достаточное кол-во визуализаций и пояснений для понимания ее содержания.

Загрузка датасета

# Импорт библиотек
from datetime import datetime

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt

# Выгрузка данных из таблицы с тренировочными данными
train_data: np.ndarray = pd.read_csv("DailyDelhiClimateTrain.csv").values

# Выгрузка данных из таблицы с тестовыми данными
test_data: np.ndarray = pd.read_csv("DailyDelhiClimateTest.csv").values

Изображение первых строк тестовой таблицы:

Ссылка на таблицу

Нормализация данных

В этой статье для удобства мы рассмотрим только температуру, но вы можете взять любой другой столбец датасета. Или даже все сразу.

Естественно, ни одна модель не сможет понять, что значит строковое представление даты »2017–01–01», так что давайте приведем значения первого столбца к целым числам (кол-во дней с начала отсчета)

Функция перевода даты в кол-во дней от 2013–01–01 (самая первая дата в таблице):

def days_since_zero_date(date_str: str) -> int:
	# Преобразование строки в объект datetime
	date_format: str = "%Y-%m-%d"
	date_obj = datetime.strptime(date_str, date_format)
	
	# Нулевая дата
	zero_date = datetime.strptime("2013-01-01", date_format)
	
	# Вычисление разницы в днях
	delta = date_obj - zero_date
	days = delta.days
	 
	return days

Теперь переведем все даты в загруженных таблицах в дни и выведем результат:

# Применяем ранее определенную функцию ко всем датам датасета
train_data[:, 0] = np.vectorize(days_since_zero_date)(train_data[:, 0])
test_data[:, 0] = np.vectorize(days_since_zero_date)(test_data[:, 0])

train_data = train_data.astype("float")
test_data = test_data.astype("float")

print(train_data[0])
# Вывод - [0 10.0 84.5 0.0 1015.6666666666666]
# Видно, что все даты превратились в дни

Далее необходимо нормализовать данные по формуле (метод Z-Нормализация)

$x_{i}' = \frac{x_{i} - \overline{X}}{\sigma_{x}}$

Где:

$\overline{X}$ — среднее значение выборки
$\sigma_{x}$ — стандартное отклонение выборки
$x_{i}$ — ненормализованное значение
$x_{i}'$ — нормализованное значение

class Normalize:
	def __init__(self, data: np.ndarray) -> None:
		self.data: np.ndarray = np.copy(data) # Записываем копию данных
		
		# Вычисляем среднее по каждому столбцу
		self.__mean: np.ndarray = data.mean(axis=0)
		# Вычисляем стандартное отклонение по каждому столбцу
		self.__std_dev: np.ndarray = data.std(axis=0)
		
	def normalizeData(self) -> np.ndarray:
		# Возврат нормализованных даннах по формуле
		return (self.data - self.__mean) / self.__std_dev
		
	def DeNormalizeData(
		self, normalized_data: np.ndarray, axes: list[int] = [0, 1, 2, 3]
	) -> np.ndarray:
		# Денормализация днанных по указанной оси
		return normalized_data * self.__std_dev[axes] + self.__mean[axes]

# Нормализация температуры
train_normalize_class = Normalize(train_data[:, 1:])
train_data[:, 1:] = train_normalize_class.normalizeData()

В данном фрагменте мы создали класс, реализующий логику нормализации данных. В двух последних строках нормализовали обучающую выборку (кроме значений дней). Метод DeNormalizeData позволяет интерпретировать любые данные, полученные с помощью модели, в привычной нам форме.

Построим график температуры для наглядности.

# Создаем поле графика
fig, ax = plt.subplots(1, 2)

# Лимиты на осях
ax[0].set_ylim([-10, 40])
ax[1].set_ylim([-10, 40])

# Подписи осей
ax[0].set_ylabel("Темперетура")
ax[0].set_xlabel("День")
ax[1].set_xlabel("День")

ax[0].set_title("Нормализованная температура")
ax[1].set_title("Реальная температура")

# Сетка на осях
ax[0].grid()
ax[1].grid()

# Отображение нормализованных и ненормализованных данных
ax[0].plot(train_data[:, 1], c="b", linewidth=1)
ax[1].plot(
	train_normalize_class.DeNormalizeData(train_data[:, 1], axes=[0]),
	c="r",
	linewidth=1,
)

plt.show()

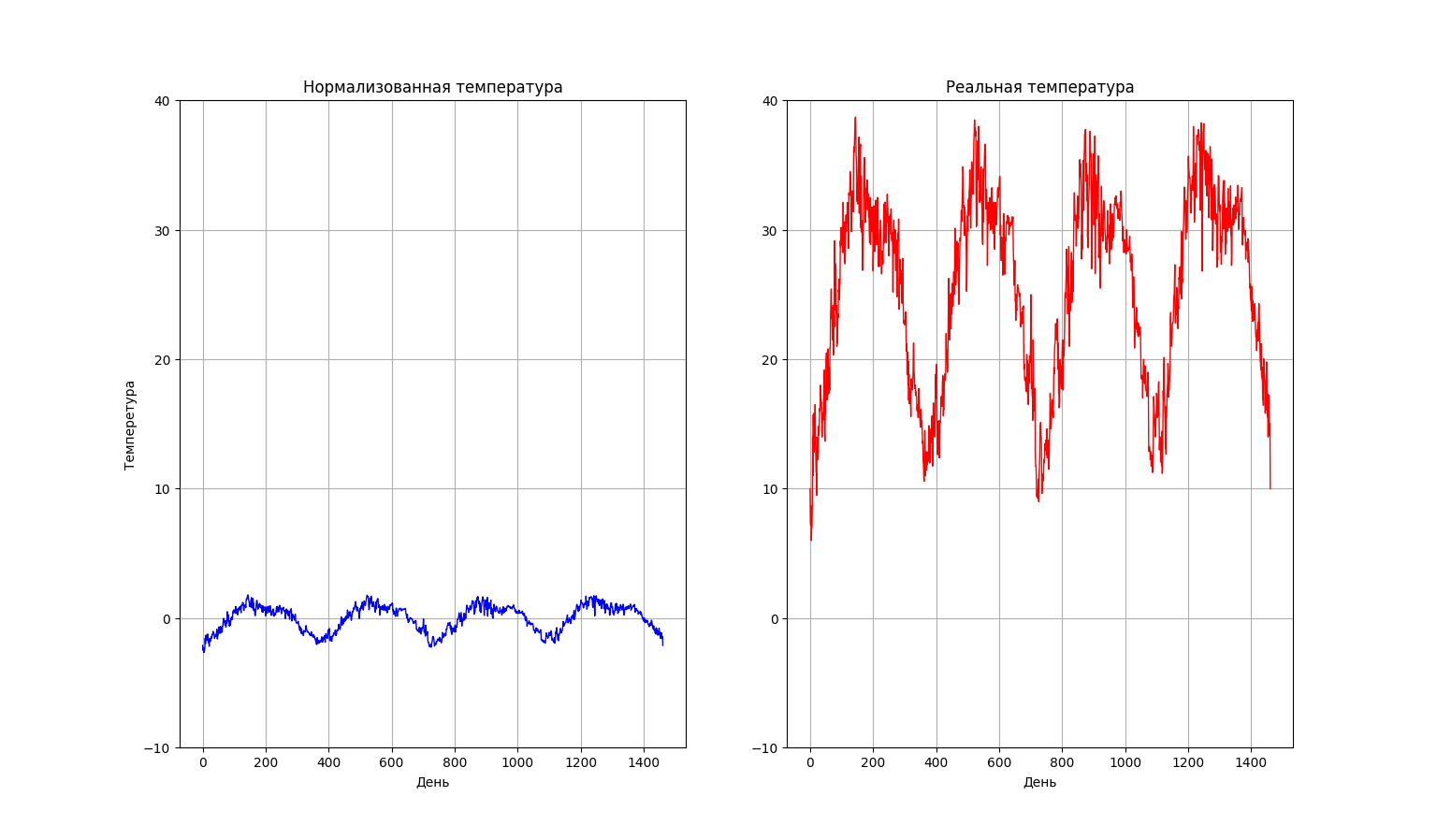
Видно, что нормализованные данные не потеряли свою информационную ценность, легко восстанавливаются в реальные данные (второй график) и более удобны для анализа с помощью моделей машинного обучения. О пользе нормализации

Сглаживание шума

Сглаживать шум будем методом скользящей средней. Суть метода в том, что мы проходимся по всему графику «окном» определенного размера. Перемещая окно, вычисляем среднее всех значений, которые в него попали. Таким образом мы сглаживаем весь шум графика, так как он компенсирует сам себя.
На самом деле, для решения нашей задачи применение данного метода не является обязательным, в статье он приведен скорее в образовательных целях

$SMA_{t}=\frac{1}{n}\sum^{n-1}_{i=0}p_{t-i}$

$SMA_{t}$ — значение простого скользящего среднего в точке
— количество значений исходной функции для расчёта скользящего среднего (размер «окна»)
$p_{t-i}$ — значение исходной функции в точке t-i

Пример использования (взято из интернета)

Реализация в коде с помощью pandas:

window_size = train_data.shape[0] // 70
denoised_data: np.ndarray = (
	pd.Series(train_data[:, 1])
	.rolling(window=window_size)
	.mean()
	.iloc[window_size - 1 :]
	.values
)

Результат:

Я не буду прикреплять код построения графика, так как ничего нового вы там не найдете.

Прогнозирование данных

Видно, что график температуры обладает ярко выраженной периодичностью и сильно напоминает синусоиду.
Из этого вытекает цель — подобрать наиболее подходящую синусоиду (или сумму синусоид), которая будет наилучшим образом соответствовать температуре.

Подбор подходящей кривой с помощью преобразования Фурье и градиентного спуска.

Преобразование Фурье

Преобразование Фурье — операция, которая сопоставляет первой функции вторую: вторая функция описывает коэффициенты («амплитуды») при разложении первой функции на элементарные составляющие — гармонические колебания с разными частотами. То есть фактически данное преобразование раскладывает функцию на сумму синусов разной частоты.

Формально преобразование определяется так:

$G(t) = \int_{-\infty}^{\infty} g(t) e^{-2\pi ift} \, dt$

Где — исследуемый диапазон частот, а G(t) — амплитуда синусоиды частоты , которая является слагаемым исходной функции.
Для более подробного ознакомления с концепцией преобразования Фурье советую посмотреть данное видео

Визуализация преобразования

Таким образом, если мы возьмем несколько синусоид максимальной амплитуды (те, которые лучше всего аппроксимируют наши данные) и построим график их суммы, то мы получим неплохую аппроксимацию температуры (в нашем случае).

Но, к сожалению, преобразование Фурье не выдает нам все веса идеальной функции, но и нам нужна только частота, ведь остальные параметры мы получим с помощью метода градиентного спуска. Но давайте по порядку и в коде:

# Значения на оси X (абсциссе), на основе которых модель будет делать предсказания
x_data:np.ndarray = np.linspace(0, len(denoised_data), len(denoised_data))

# Дискретное Преобразование Фурье, список амплитуд
mfft:np.ndarray = np.fft.fft(denoised_data)

# Получаем индексы частот, которые соответствуют самым значимым (с высокой амплитудой) синусоидам.
imax:np.ndarray = np.argsort(np.absolute(mfft))[::-1]

Для простоты мы будем раскладывать наши данные на сумму пяти синусоид. Не будем брать слишком много слагаемых, чтобы модель не потеряла обобщающую способность.

# Кол-во синусов, которые мы будем суммировать
number_of_sinuses: int = 5

# Берем первые number_of_sinuses самых высоких амплитуд (они соответствуют частотам)
imax = imax[:number_of_sinuses]

# Вычисляем частоту каждой синусоиды
frequency:np.ndarray = np.array(imax) / len(denoised_data)

Оптимизация параметров

Для начала определим функцию, которая будет аппроксимировать наши данные о температуре. Из-за того, что мы рассматриваем сумму пяти синусов, то определение нашей модели напрашивается само:

$Y(w, x) = b + \sum_{i=0}^{4} w_{3i}\sin(w_{3i+1}x + w_{3i+2})$

Теперь нужно инициализировать наши параметры так, чтобы их получилось верно оптимизировать (большинство моделей плохо оптимизируют параметры тригонометрических функций со случайно инициализированной частотой).

Параметр $w_{3i}$ будем инициализировать значением стандартного отклонения всей выборки ( $w_{3i} = \sigma_{x}$ ).
Параметр $w_{3i+1}$ (самый важный) будем инициализировать полученной частотой (умноженной на $2\pi$ ) для каждого синуса соответственно ( $w_{3i+1}=2\pi f_{i}$ ). Это нужно сделать, чтобы модель не подбирала частоту волны, в противном случае параметры не будут оптимизированы.
Параметр сдвига по абсциссе мы инициализируем
Параметр мы инициализируем математическим ожиданием выборки ( $b = \overline{X}$ )

# Начальные параметры
init_params: np.ndarray = np.array(
	[
		np.array([np.std(denoised_data), frequency[i] * 2 * np.pi, 0.0])
		for i in range(number_of_sinuses)
	]
)

bias: float = np.mean(denoised_data)

Оптимизируем наши параметры путем градиентного спуска в связке с оптимизатором Adam. В качестве функции ошибки модели используем MSE .

Функция ошибки (MSE), которую наш алгоритм будет пытаться минимизировать

$MSE = \frac{1}{n}\sum_{i=1}^{n}(y-\overline y)^{2}$

— реальное значение целевой переменной (метка)
$\overline y$ — предсказание модели

Градиентный спуск
Градиентный спуск заключается в том, что по мере обучения модели мы вычитаем из каждого веса значение его локальной частной производной от функции ошибки. Данный алгоритм приводит к ее минимизации, то есть к наиболее точным ответам модели. Определение:

$w_{n} = w_{n} - \frac{\delta E}{\delta w_{n}}\cdot \eta$

— функция ошибки
$w_{n}$ — данный вес
$\eta$ — коэффициент скорости обучения (чем больше, тем агрессивнее обучается модель, часто выбирают $10^{-3}$ )

Оптимизатор Adam (необязательно для прочтения)
Идея Adam заключается в том, чтобы адаптивно изменять скорость обучения для каждого веса на основе двух моментов первого и второго порядков градиента. Веса с большим градиентом получают меньший шаг, а веса с меньшим градиентом получают больший шаг.

Оптимизатор работает по данному алгоритму:
$m_t = \beta_1 m_{t-1} + (1 - \beta_1)g_t$
$v_t = \beta_2 v_{t-1} + (1 - \beta_2)g_t^2$
$\hat{m_t} = \frac{m_t}{1 - \beta_1^t}$
$\hat{v_t} = \frac{v_t}{1 - \beta_2^t}$

Оптимизация весов:

$w_t = w_{t-1} - \frac{\eta}{\sqrt{\hat{v_t}}+\epsilon} \hat{m_t}$

Где:
— номер итерации
w_t — вектор весов в момент времени
g_t — вектор градиентов в момент времени
m_t — оценка первого момента (среднего значения) градиента в момент времени
v_t — оценка второго момента (среднего квадрата) градиента в момент времени
$\beta_1$ и $\beta_2$ — параметры, обычно равные 0.9 и 0.999 соответственно
$\eta$ — скорость обучения
$\epsilon$ — малое число, используемое для стабилизации деления

Пример поиска минимумов функции методом градиентного спуска

Модель

Создадим модель с помощью библиотеки tensorflow. Остальные популярные варианты (например, scipy) представляют скудные возможности для определения и визуализации обучения, так что напишем собственную модель и обучим ее.

Важно! Так как оптимизатор Adam обладает стохастической природой, нужно выполнить команду tf.random.set_seed(), чтобы все, кто запустит код получили одинаковые результаты.

Определение функционала модели и ее параметров (с помощью keras.layers.Layer)

# Импорт модулей
import tensorflow as tf
from keras import layers
from keras.optimizers import Adam

tf.random.set_seed(8)

# Определяем слой
class SinLayer(layers.Layer):
	def __init__(self): # Инициализируем методы и атрибуты родительского класса
		super(SinLayer, self).__init__()
		
	def build(self, _): # Задаем начальные параметры
		self.kernel = self.add_weight(
			"kernel", shape=(number_of_sinuses, 3), trainable=True
		) # Веса модели
		
		# Свободный коэффициент
		self.bias = self.add_weight(name="bias", shape=(), trainable=True) 
		
	def call(self, inputs): # Реализация функционала нашей модели (ранее в статье)
		result: float = 0
		for i in range(number_of_sinuses):
			result += self.kernel[i][0] * tf.sin(
				self.kernel[i][1] * inputs + self.kernel[i][2]
			)
		return result + self.bias # Результат работы модели

Теперь определим саму модель и скомпилируем ее:

# Определение модели
model = tf.keras.Sequential(
	[
		layers.Input(shape=(1,)),
		SinLayer(),
	]
)

# Компилируем модель оптимизатором Adam (с наиболее подходящими параметрами)
# и ошибкой MSE
model.compile(Adam(0.001, 0.8, 0.9), "mean_squared_error")

# Задаем модели ранее определенные веса для правильной оптимизации весов
model.set_weights([init_params, bias])

Теперь обучим нашу модель на тренировочных данных и построим график изменения ошибки по мере обучения.

# Получаем историю ошибки модели
history = model.fit(x_data, denoised_data, epochs=70)

# Отображаем ее на графике
plt.plot(history.history["loss"])
plt.grid()
plt.xlabel("Эпоха")
plt.ylabel("Значение ошибки MSE на данной эпохе")
plt.show()

Эпоха — это количество полных прохождений всего датасета. Чем больше эпох, тем лучше натренирована нейросеть.

Видно, что ошибка модели сильно уменьшилась, значит, она натренировалась

Важное замечание! К ответу регрессионной модели принято добавлять случайный шум (мы тоже так будем делать):

$y = Y(w, x) + \epsilon$

Теперь посмотрим, как наша модель предсказывает данные тренировочной выборки. Для этого также построим график (но перед отображением нужно обязательно денормализовать данные с помощью ранее определенного метода DeNormalizeData):

Видно, что наша модель успешно уловила все тренды и периодизацию. Хороший результат.

Вычисление ошибки модели на тестовой выборке

Для вычисления ошибки модели будем использовать функцию MAE:

$MAE(y, \overline{y}) = \frac{1}{n}\sum\mid y-\overline{y}\mid$

Фактически, данная ошибка — среднее отклонение предсказанных данных от действительных.

Вычислим ошибку на тестовой выборке (на денормализованных, реальных данных):

# Определяем функцию ошибки
def MAE(predictions: np.ndarray, labels: np.ndarray) -> float:
	return np.mean(np.abs(predictions - labels))

# Выводим значение ошибки
print(
	MAE(
		train_normalize_class.DeNormalizeData(
			model(test_data[:, 0]).numpy().T[0], axis=[0]
		) + np.random.normal(size=test_data[:, 0].shape),
		test_data[:, 1],
	)
)

Мы выполняем преобразование data.numpy().T[0] из-за того, что модель выводит тензор Tensorflow формы (114, 1). Данное преобразование переводит ответ модели в вектор numpy и выделяет 114 элементов, которые являются ответом

После выполнения кода ошибка модели составила 2.2743354568119476 градусов цельсия. То есть наша регрессионная модель предсказывает температуру на 114 дней (длина тестовой выборки) вперед с погрешностью чуть более 2 градусов.

Заключение

Кроме методов, рассмотренных выше, существует множество различных способов анализировать и прогнозировать временные ряды. К ним относятся нейросети и прочие математические приемы.

Материалы из статьи:

Тем, кому интересна концепция прогнозирования временных рядов, могу посоветовать: