Анализ класса нестационарных процессов со стационарными приращениями на фондовых рынках07.02.2017 14:48

Цель данной статьи — поделиться результатами исследования по выявлению структуры в значениях цен акций, которые торгуются на Московской Бирже и на NYSE, методом их проверки на стационарность с помощью теста Дики-Фуллера.

Есть небольшой класс акций, который представляет собой нестационарный процесс со стационарными приращениями и распределение t-статистики которого ведёт себя довольно любопытным образом, а именно не стремится к стандартному нормальному распределению при увеличении количества наблюдений. Как такие акции выявлять?

Сбор данных

Первая вещь, которая нам потребуется — это список тикеров, которыми реально можно торговать через одного из брокеров. Тикер — это краткое название в биржевой информации котируемых инструментов (в данном случае, акций). Я начну с российского фондового рынка. У нас самая популярная биржа — московская, поэтому поговорим про неё.

В какой-то момент своей жизни я пошла в офлайн и заключила со Сбербанком договор брокерского обслуживания. При таком раскладе список тикеров можно получить довольно просто. Достаточно загрузить систему QUIK, заказать поток котировок для акций:

затем вывести их на вкладку Торговля и сохранить таблицу в файл. Всего получается 296 тикеров. Если не очень хочется устраивать себе квест, то список тикеров можно найти в разделе Примеры данных на сайте Московской биржи. Единственное, возможно, этот список устарел.

Вторая вещь, которая нам нужна, — это данные о ценах акций. Сколько их нужно для составления адекватной картины рынка и за какой именно промежуток их брать — это предмет споров. Техническое ограничение, с которым мы столкнёмся дальше — это минимум 10 значений для каждой акции.

Мне захотелось по полученным ранее тикерам взять данные о ценах закрытия акций за 2016 год (252 торговых дня), но можно брать данные и за меньший промежуток, можно вообще проводить исследования внутри дня. По большому счёту, нам сейчас не так важно, какие именно данные мы возьмём. Единственное, если мы пойдём на Московскую Биржу и запросим у неё архивные данные за 2016 год, то она нам скажет, что за всё это дело нужно заплатить 32 400 рублей (раньше, кстати, данные стоили ещё дороже). Я из вредности написала парсер.

На самом деле, гораздо быстрее достать данные с финама или с Yahoo Finance, но почему-то это не так весело. Я в своё время даже связалась с руководителем группы информационного аудита и спросила, могу ли я парсить их сайт для научных исследований. Мне разрешили.

[Здесь было много букв и кода про парсер, но я всё удалила, потому что это, наверное, не очень интересно. Если я ошибаюсь, пишите, — опубликую парсер отдельной статьёй.]

У меня получилось собрать данные для 289 акций (по остальным данных не было). Для удобства тикеры и цены были сохранены в базе данных Microsoft SQL Server. Теперь перейдёт к математике.

Про стационарность

Если говорить про стационарность без каких-либо формул и сложных понятий, то смысл в том, что стационарный ряд не меняет со временем свои характеристики, такие как матожидание, дисперсия и ковариации.

Цену акции можно рассматривать как авторегрессионный процесс порядка 1:
$(1)$

$y_{t} = \phi y_{t-1}+\varepsilon_{t},$

где $\phi$ — параметр модели, $\varepsilon_{t} \sim iid(0,\sigma^2)$ — белый шум, $t=1,...,n$ . Такой процесс является стационарным при условии $|\phi|<1$ .

Допустим, у нас есть цены акции за 252 торговых дня. Как нам по имеющимся наблюдениям определить, является ли такой авторегрессионный процесс стационарным или нет? Необходимо провести стандартную процедуру тестирования гипотезы $H_0$ : $\phi = 1$ (то есть процесс не стационарный) против альтернативной гипотезы $H_1$ : $\phi < 1$ (то есть процесс стационарный).

Про распределение Дики-Фуллера

На самом деле, с тестированием гипотезы не всё так просто, потому что если истинное значение $\phi = 1$ , t-статистика не распределена по закону Стьюдента и её распределение не стремится к стандартному нормальному при увеличении количества наблюдений. В таком случае мы не можем просто взять таблицу критических значений Стьюдента и проверить по ней гипотезу.

Под t-статистикой здесь понимается отношение отклонения оценки параметра авторегрессионной модели от его истинного значения к стандартной ошибке оценки коэффициента:

$t = \frac{\hat{\phi} - \phi}{s_{\hat{\phi}}},$

где $\hat{\phi}$ — оценка параметра авторегрессионной модели (1), $s_{\hat{\phi}}$ — стандартная ошибка оценки $\hat{\phi}$ . Оценка коэффициента $\hat{\phi}$ в альтернативной модели может выполняться с помощью обычного метода наименьших квадратов (МНК).

Впервые о том, что с t-статистикой не всё нормально, начал в 1976 году говорить Уэйн Фуллер. Потом в 1979 году они вместе с Дэвидом Дики написали любопытную статью под названием «Distribution of the Estimators for Autoregressive Time Series with a Unit Root».

На трезвую голову разобрать её почти невозможно, но именно там они представили распределение t-статистики при условии $\phi = 1$ , то есть при $t = \frac{\hat{\phi} - 1}{s_{\hat{\phi}}}$ (которое получило название статистики Дики-Фуллера), для уравнения (1) и двух его модификаций:
$(2)$

$y_{t} = a + \phi y_{t-1}+\varepsilon_{t},$

$(3)$

$y_{t} = a + \phi y_{t-1}+ct+\varepsilon_{t}.$

Для уравнения (1) распределение Дики-Фуллера имеет вид:

$\lim t_1 = \frac{W^2(1)-1}{2\sqrt{\int_{0}^{1}W^2(s)ds}},$

где $t_1$ — t-статистика для процесса (1), $W(s)$ — стандартный винеровский процесс.

Критические значения статистики Дики-Фуллера приведены в книге Фуллера «Introduction to Statistical Time Series». Таким образом, для проверки авторегрессионного процесса на стационарность необходимо использовать стандартную процедуру тестирования гипотезы с тем отличием, что вместо таблицы критических значений для распределения Стьюдента необходимо использовать таблицу критический значений для распределения Дики-Фуллера.

Также важно отметить, что уравнения (1), (2) и (3) можно переписать в виде:

$y_{t} - y_{t-1} = \phi y_{t-1} - y_{t-1}+\varepsilon_{t},$

$\Delta y_{t} = (\phi - 1) y_{t-1} +\varepsilon_{t},$

$(4)$

$\Delta y_{t} = \beta y_{t-1} +\varepsilon_{t},$

$y_{t} - y_{t-1} = a + \phi y_{t-1} - y_{t-1}+\varepsilon_{t},$

$\Delta y_{t} = a + (\phi - 1) y_{t-1} +\varepsilon_{t},$

$(5)$

$\Delta y_{t} = a + \beta y_{t-1} +\varepsilon_{t},$

$y_{t} - y_{t-1} = a + \phi y_{t-1} - y_{t-1}+ ct +\varepsilon_{t},$

$\Delta y_{t} = a + (\phi - 1) y_{t-1}+ ct +\varepsilon_{t},$

$(6)$

$\Delta y_{t} = a + \beta y_{t-1}+ ct +\varepsilon_{t},$

где $\Delta y_{t} = y_{t} - y_{t-1}$ , а $\beta = \phi - 1$ . Процессы (4), (5) и (6) могут быть оценены и протестированы при $\beta = 0$ аналогично тестированию гипотезы при $\phi = 1$ . Следовательно, статистика Дики-Фуллера позволяет осуществлять проверку на стационарность не только самого процесса, но и его разностей первого порядка.

Про тест Дики-Фуллера

Тест Дики-Фуллера есть во всех стандартных пакетах, поэтому мы можем проверить цены акций, полученные на этапе сбора данных, на стационарность, например, в MATLAB. Ниже приведён код, в котором устанавливается соединение с базой данных Microsoft SQL Server (где хранятся значения цен акций и тикеры) и создаются два массива. Первый — непосредственно для цен, второй — только для тех тикеров, для которых есть данные о ценах:

conn = database.ODBCConnection('uXXXXXX.mssql.masterhost.ru', 'uXXXXXX', 'XXXXXXXXXX');
curs = exec(conn, 'SELECT ALL PriceId, StockId, Date, Price FROM StockPrices');
curs = fetch(curs);
data = curs.Data
idsArr = unique(cell2mat(data(:,2)));
sqlquery = 'SELECT ALL StockId, ShortName, Code FROM Stocks WHERE StockId IN (';
for i=1:length(idsArr)
    if i==length(idsArr)
        sqlquery = strcat(sqlquery,int2str(idsArr(i)),')');
    else
        sqlquery = strcat(sqlquery,int2str(idsArr(i)),',');
    end
end
curs = exec(conn, sqlquery);
curs = fetch(curs);
names = curs.Data
close(conn);

Тест Дики-Фуллера выполняется с помощью функции adftest, которая на вход принимает одномерный временной ряд, а на выходе возвращает логическое значение, равное 1, если нулевая гипотеза отвергается в пользу альтернативной, и 0 — иначе. Выполним тест Дики-Фуллера при 5%-ном уровне значимости для модели вида (1):

for i = 1:length(names)
    % Indexes with current stock's data
    indexes = find(cell2mat(data(:,2)) == cell2mat(names(i,1)));
    isStat(i) = adftest(cell2mat(data(indexes,4)));
end
% Indexes with stationary stocks
stat = find(isStat == 1);

Программа 5 раз отвергает нулевую гипотезу в пользу альтернативной модели. Изобразим эти временные ряды:

for i=1:length(stat)
    indexes = find(cell2mat(data(:,2)) == cell2mat(names(stat(i),1)));
    figure
    plot(datetime(data(indexes,3)), cell2mat(data(indexes,4)))
    legend(names(stat(i),3));
end

Посмотрим на график изменения цены одной из акций.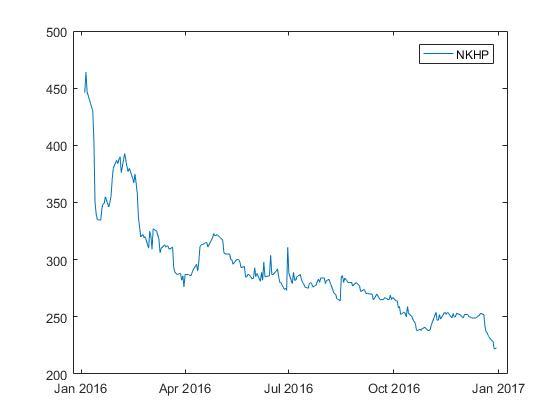

Здесь видно, что временной ряд цены акции не является стационарным.

Построим разности первого порядка для данного временного ряда.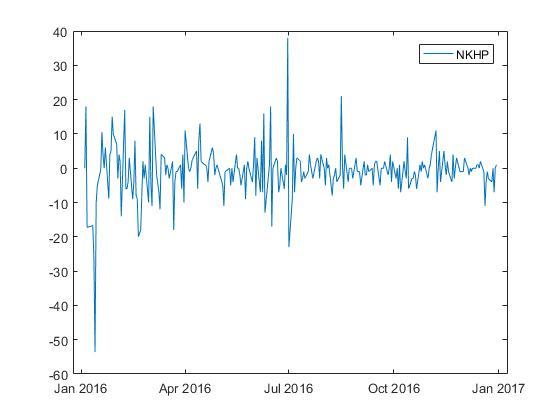

Похоже, разности первого порядка для временного ряда цены акции действительно удовлетворяют условию стационарности.

Результаты на NYSE

Те же самые исследования были проведены и для американского фондового рынка, а именно для Нью-Йоркской фондовой биржи. Список тикеров был взят с сайта NASDAQ. Там на данный момент 2714 адекватных тикеров. Данные о ценах были взяты с Yahoo Finance. Нашлось 2647 тикеров, для которых есть данные о ценах акций за 2016 год, и в результате тестирования на стационарность получилось 26 акций со стационарными приращениями.

Выводы

На фондовых рынках существует небольшое количество акций, для которых изменение цены является процессом со стационарными приращениями первого порядка. Наличие таких процессов даёт почву для дальнейших исследований и стабильного извлечения прибыли, но об этом мы поговорим в следующий раз.

Что почитать по теме?

Магнус, Я.Р. Эконометрика. Начальный курс / Я.Р. Магнус, П.К. Катышев, А.А. Пересецкий. — М.: Дело, 2004. — 576 с.

Это очень хороший учебник по эконометрике, ничуть не хуже чем буржуйский, и написан нормально, так что можно разобраться.