Анализ безопасности хранения и хеширования паролей при помощи алгоритма MD5
С появлением компьютерных технологий стало более продуктивным хранить информацию в базах данных, а не на бумажных носителях. Веб-приложения, нуждающиеся в аутентификации пользователя, обычно проверяют входные пароли, сравнивая их с реальными паролями, которые обычно хранятся в частных базах данных компании. Если злоумышленники получат доступ к вышеупомянутой базе данных личные данные пользователей будут утеряны. В настоящее время базы данных используют хеш-алгоритмы для защиты хранящихся паролей, но проблемы, связанные с безопасностью все еще актуальны. Каждый год хакеры опубликовывают большой список взломанных паролей от известных социальных сетей или же хранилищ данных. Подобные атаки оказались успешными благодаря использованию слабого алгоритма хеширования.
Криптографические хеш-функции, чаще называемые просто хешем, — незаменимый и повсеместно распространенный инструмент, используемый для выполнения целого ряда задач, включая аутентификацию, проверку целостности данных, защиту файлов и даже обнаружение зловредного ПО. Это математический алгоритм, преобразовывающий произвольный массив данных в состоящую из букв и цифр строку фиксированной длины. Причем при условии использования того же типа хеша эта длина будет оставаться неизменной, вне зависимости от объема вводных данных [2]. Существует масса алгоритмов хеширования, отличающихся криптостойкостью, сложностью, разрядностью и другими свойствами. Считается, что идея хеширования принадлежит сотруднику IBM, появилась около 50 лет назад и с тех пор не претерпела принципиальных изменений. В наши дни хеширование обрело массу новых свойств и используется в очень многих областях информационных технологий.
Алгоритм хеширования сообщений MD5 — это 5-я версия алгоритма хеширования сообщений, разработанного Роном Ривестом в 1991 году для получения 128-битного выходного сообщения. Эта версия [5] была представлена как улучшенная c точки зрения надежности относительно предыдущего алгоритма MD4.
Преобразование сообщения произвольной длины в хеш-значение подразумевает работу пяти шагов алгоритма, каждый из которых имеет свою определенную задачу. Рассмотрим подробнее шаги алгоритма:
Шаг 1: Выравнивание потока
Необходимо добавление дополнительных битов к исходному сообщению, выполненное таким образом, чтобы длина исходного сообщения с добавочными битами была эквивалентна 448 по модулю 512. Добавление выполняется даже в том случае, если длина исходного сообщения уже сравнима с 448. В битах заполнения только первый бит равен 1, а остальные биты равны 0.
Шаг 2. Добавление длины сообщения
В конец сообщения дописывают 64-битное представление длины данных (количество бит в сообщении) до выравнивания. На этом этапе полученное сообщение имеет длину, кратную 512 битам. Вычисления будут основываться на представлении этого потока данных в виде массива слов по 512 бит.
Шаг 3: инициализация MD-буфера
Буфер из четырех слов (A, B, C, D) используется для вычисления значений для дайджеста сообщения. Здесь A, B, C, D являются 32 — разрядными регистрами, состоящие из шестнадцатеричных чисел и инициализируются следующим образом
Word A | 01 | 23 | 45 | 67 |
Word B | 89 | AB | CD | EF |
Word C | FE | DC | BA | 98 |
Word D | 76 | 54 | 32 | 10 |
Шаг 4: обработка сообщения в цикле
MD5 использует четыре вспомогательные функции, которые принимают на вход три 32-битных числа и производят 32-битный вывод [1].

Эти функции используют логические операторы типа OR, XOR, AND, NOT. Содержимое четырех буферов смешивается с входными данными (из предыдущего шага) с помощью вспомогательного буфера, который строится на основе вычислений со вспомогательными функциями. Выполняется четыре раунда, в каждом из которых используется своя вспомогательная функция.
Шаг 5. Результат вычислений
После выполнения всех раундов буфер A, B, C, D содержит вывод MD5, это и есть хеш.
Для того чтобы повысить безопасность хранения паролей алгоритм MD5 может использоваться для хеширования исходных паролей. Таким образом в базе данных будут храниться значения хеш-функции соответствующего алгоритма, а не открытого текста. Во время аутентификации входной пароль также хешируется алгоритмом MD5 на стороне клиента аналогичным образом, и результирующее хеш-значение сравнивается с значением в базе данных для конкретного пользователя.
Криптоанализ алгоритма MD5 говорит о том, что на данный момент существуют несколько видов «взлома» хешей MD5:
1) атаки переборного типа
В криптографии атака полного перебора или исчерпывающий поиск — ключей- это стратегия, которая теоретически может быть использована против любых зашифрованных данных. Злоумышленник, который не может воспользоваться слабостью в системе шифрования, реализовывает атаку подобного типа. Она включает в себя систематическую проверку всех возможных ключей, пока не будет найден правильный. В худшем случае для взлома сообщения потребуется задействовать всю вычислительную мощность.
Перебор по словарю — атака на систему защиты, применяющая метод полного перебора предполагаемых паролей, используемых для аутентификации, осуществляемого путём последовательного пересмотра всех слов (паролей в чистом виде) определённого вида и длины из словаря с целью последующего взлома системы и получения доступа к секретной информации [7].
Как видно из определения атаки по словарю являются атаками полного перебора. Единственное отличие состоит в том, что данные атаки обычно более эффективны так как становится не нужным перебирать все комбинации символов, чтобы добиться успеха. Злоумышленники используют обширные списки наиболее часто используемых паролей таких как, имена домашних животных, вымышленных персонажей или конкретно характерных слов из словаря — отсюда и название атаки. Однако если пароль действительно уникален (не является комбинацией слов), атака по словарю не сработает. В этом случае использование атаки полного перебора — единственный вариант.
Для полного перебора или перебора по словарю можно использовать программы PasswordsPro, MD5BFCPF, John the Ripper.
2) атаки в которых применяются радужные таблицы
Радужные таблицы состоят из хеш-цепочек и более эффективны, чем предыдущий упомянутый тип атак, поскольку они оптимизируют требования к хранению, хотя поиск выполняется немного медленнее. Радужные таблицы отличаются от хеш-таблиц тем, что они создаются с использованием как хеш-функций, так и функций редукции [4].
Пусть существует хеш-функция H с длиной хеша n и конечное множество паролей P. Хеш-таблица должна справляться с главной задачей: содержать структуру данных, которая для любого значения хеша h может либо найти такой элемент p из P, что H (p)=h, либо определить, что такого элемента не существует. Простейший способ сделать это — вычислить H (p) для всех p из P, но для хранения такой таблицы, как выяснилось ранее потребуется слишком много памяти поэтому стоит обратиться к хеш-цепочкам.
Цепочки хешей — метод для уменьшения требования к объёму памяти. Главная идея — определение функции редукции R, которая сопоставляет значениям хеша значения из P. Стоит отметить, что R не является обращением хеш-функции. Рассмотрим подробнее построение хеш-цепочки [11]:
1) Каждое звено именуется результатом хэш-функции над полями данных этого звена;
2) Каждое звено кроме первого обязательно имеет поле данных с именем предыдущего звена.

Таким образом вся цепочка имеет сквозную зависимость, направленную к первому звену, хеш последнего звена фактически является цифровым отпечатком всей цепочки.
Начиная с исходного пароля и попеременно применяя к каждому полученному значению H и R, получается цепочка перемежающихся паролей и хешей.
Для каждого хеша h, значение которого нужно хотим обратить (найти соответствующий ему пароль), вычисляем последовательность R (…R (H (R (h)))…). Если какое-то из промежуточных значений совпадёт с каким-нибудь концом какой-либо цепочки, следует взять начало этой цепочки и восстанавливаем её полностью. С высокой вероятностью полная цепочка будет содержать значение хеша h, а предшествующий ему пароль будет искомым.
Радужные таблицы являются развитием идеи таблицы хеш-цепочек. Функции редукции применяются по очереди, перемежаясь с функцией хеширования: H, R1, H, R2, …, H, Rk.
Использование последовательностей функций редукции изменяет способ поиска по таблице. Поскольку хеш может быть найден в любом месте цепочки, необходимо сгенерировать k различных цепочек.
Существует множество систем взлома паролей и веб-сайтов, которые используют подобные таблицы. Основная идея данного метода — достижение компромисса между временем поиска по таблице и занимаемой памятью. Конечно, использование радужных таблиц не гарантирует 100% успеха взлома систем паролей. Однако, чем больше набор символов, используемый для создания радужной таблицы, и чем продолжительнее хеш-цепочки, тем больше будет шансов получить доступ к базе данных исходных паролей.
Коллизии MD5
Одно из главных свойств и требований к хеш-функциям это относительная невозможность (с точки зрения вычислений) по получению одинакового значения хеша для разных входных сообщений и идентичного начального буфера. Коллизии существуют для большинства хеш-функций, но для «хороших» функций частота их возникновения близка к теоретическому минимуму.
MD5 был тщательно изучен криптографическим сообществом с момента его первоначального выпуска и до 2004 года демонстрировал лишь незначительные недостатки. Однако летом 2004 года криптографы Ван Сяоюнь и Фэн Дэнго продемонстрировали алгоритм способный генерировать MD5-коллизии с использованием стандартного вектора инициализации.
Исследование [10] показало, что можно создать два 512-битных входных блока и изменить определенные биты внутри этих блоков, чтобы создать два слегка отличающихся сообщения с одинаковым хэш-значением. Время создания пары сообщений MD5 составляло в среднем 1 час. Пример подобной пары сообщений, дающий одинаковый хеш представлен ниже (различающиеся разряды выделены):
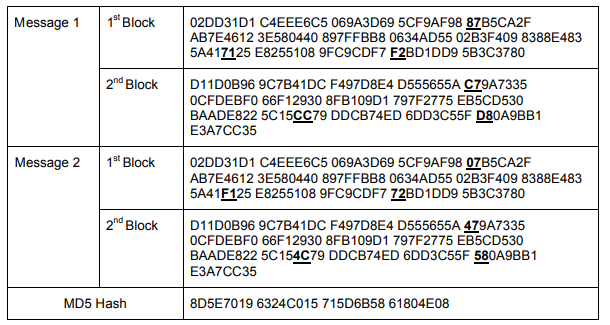
Позже данный алгоритм был усовершенствован, как следствие время поиска пары сообщений значительно уменьшилось, что позволило находить коллизии с приемлемой вычислительной сложностью. Как оказалось, в MD5 вопрос коллизий не решается.
Факторы, влияющие на безопасность пароля и возможные решения
Информационная энтропия
Надежность и сложность пароля в сфере информационных технологий обычно измеряется в терминах теории информации. Чем выше информационная энтропия, тем надежнее пароль и, следовательно, тем труднее его взломать.
где N и L — количество возможных символов и количество символов в пароле соответственно. H измеряется в битах. [9]
Как видно, чем длиннее пароль и чем больше набор символов, из которого он получен, тем он надёжнее. Правда вместо количества попыток, которые необходимо предпринять для угадывания пароля, принято вычислять логарифм по основанию 2 от этого числа, и полученное значение называется количеством «битов энтропии» в пароле. При увеличении длины пароля на один бит количество возможных паролей удвоится, что сделает задачу атакующего в два раза сложнее. В среднем атакующий должен будет проверить половину из всех возможных паролей до того, как найдет правильный. В качестве наилучшей практики должно выполняться предварительное требование: приложение настаивает на том, чтобы пользователь использовал надежный пароль в процессе регистрации.
Добавление «соли» к паролю
Одна из наиболее распространенных причин успешных атак заключается в том, что компании не используют добавление соли к исходному паролю. Это значительно облегчает хакерам взлом системы с помощью атак типа радужных таблиц, особенно учитывая тот факт, что многие пользователи используют очень распространенные, простые пароли, имеющие одинаковые хеши. Соль-это вторичный фрагмент информации, состоящий из строки символов, которые добавляются к открытому тексту (исходному паролю пользователя), а затем хешируется [8]. Соление делает пароли более устойчивыми к атакам типа радужных таблиц, так как подобный пароль будет иметь более высокую информационную энтропию и, следовательно, менее вероятное существование в предварительно вычисленных радужных таблицах. Как правило, соль должна быть не менее 48 бит. Добавление соли можно осуществить следующими способами:
1) Использование единой соли для всех паролей: учитывая, что соль достаточно длинная и сложная, стандартная радужная таблица не может быть использована для расшифровки соленых хешей. Однако два одинаковых пароля все равно будут иметь один и тот же хеш.
2) Использование различной (случайной) соли для каждого пароля и хранение соли в самой базе данных: если мы используем разные соли для каждого пароля, то два одинаковых пароля будут иметь разные хеши. Злоумышленник должен генерировать различные радужные таблицы для каждого отдельного пользователя, что делает его вычислительно сложнее для взлома. Соли могут храниться в открытом виде в базе данных. Цель соли не в том, чтобы быть неизвестной, а в том, чтобы быть достаточно случайной, чтобы препятствовать использованию радужных таблиц.
3) Использование существующего значения столбца. Существующее значение столбца, например, username, можно использовать в качестве соли. Это решение аналогично второму решению, рассмотренному выше. Оно препятствует использованию стандартной радужной таблице, но тем не менее хакер может создать радужную таблицу для определенного имени пользователя, например, «root» или «admin».
Заключение
Как уже отмечалось ранее, основная задача любой функции хеширования сообщений − производить образы, которые можно считать относительно случайными. Чтобы считаться криптографически безопасной, хэш-функция должна отвечать двум основным требованиям: во-первых, злоумышленник не может сгенерировать сообщение, соответствующее определенному хеш-значению и во-вторых, невозможно создать два сообщения, которые производят одно и то же значение. К сожалению, выяснилось, что алгоритм MD5 не способен отвечать данным требованиям. IETF (Internet Engineering Task Force) рекомендовала новым проектам протоколов не использовать MD5 так как исследовательские атаки предоставили достаточные основания для исключения использования алгоритма в приложениях, которым требуется устойчивость к различного рода коллизиям.
Хеши MD5 больше не считаются безопасными, и их не рекомендовано использовать для криптографической аутентификации.
Ссылки на источники и литература:
1. MD5 // wikipedia.org URL: https://ru.wikipedia.org/wiki/MD5#:~: text=MD5%20%E2%80%94%20%D0%BE%D0%B4%D0%B8%D0%BD%20%D0%B8%D0%B7%20%D1%81%D0%B5%D1%80%D0%B8%D0%B8%20%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC%D0%BE%D0%B2,%D0%9E%D0%BF%D0%B8%D1%81%D0%B0%D0%BD%20%D0%B2%20RFC%201321. (дата обращения: 20.11.2020).
2. A.П. Алферов, А.Ю. Зубов, А.С. Кузьмин, А.В. Черемушкин. Основы криптографии. 2-е издание, М. Гелиос АРВ-2006.
3. Коллизия хеш-функции // wikipedia.org URL: https://ru.wikipedia.org/wiki/MD5#:~: text=MD5%20%E2%80%94%20%D0%BE%D0%B4%D0%B8%D0%BD%20%D0%B8%D0%B7%20%D1%81%D0%B5%D1%80%D0%B8%D0%B8%20%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC%D0%BE%D0%B2,%D0%9E%D0%BF%D0%B8%D1%81%D0%B0%D0%BD%20%D0%B2%20RFC%201321. (дата обращения: 5.12.2020).
4. Радужная таблица // wikipedia.org URL: https://ru.wikipedia.org/wiki/%D0%A0%D0%B0%D0%B4%D1%83%D0%B6%D0%BD%D0%B0%D1%8F_%D1%82%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D0%B0 (дата обращения: 2.12.2020).
5. Rivest, R. (1992, April). The MD5 Message Digest Algorithm. Request for Comments (RFC) 1321. Retrieved from https://www.rfceditor.org/rfc/rfc1321.txt
6. Kioon M. C, Wang Z. S, Shubra D.D Security Analysis of MD5 Algorithm in Password Storage // Scientific.Net. 2013. С. 2706–2711.
7. Нечаев В.И. Элементы криптографии (Основы теории защиты информации): Учеб. Пособие для ун-тов и пед. вузов./ Под ред. В.А. Садовничьего — М.: Высш. шк., 1999.
8. John Black, Martin Cochran, Trevor Highland Fast Software Encryption. FSE изд. 2006. С. 262–277.
9. Информационная энтропия // ru.wikipedia.org/ URL: https://ru.wikipedia.org/wiki/%D0%98%D0%BD%D1%84%D0%BE%D1%80%D0%BC%D0%B0%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D0%B0%D1%8F_%D1%8D%D0%BD%D1%82%D1%80%D0%BE%D0%BF%D0%B8%D1%8F (дата обращения: 12.11.2020).
10. How to Break MD5 and Other Hash Functions // https://link.springer.com/chapter/10.1007/11426639_2 (дата обращения: 17.10.2020).
11. Структуры данных / Хэш-цепочки // medium.com URL: https://medium.com/dtechlog/%D1%81%D1%82%D1%80%D1%83%D0%BA%D1%82%D1%83%D1%80%D1%8B-%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B%D1%85-%D1%85%D1%8D%D1%88-%D1%86%D0%B5%D0%BF%D0%BE%D1%87%D0%BA%D0%B8–659439754831 (дата обращения: 10.12.2020).
