Аналитическое вычисление производных на шаблонах C++20.09.2016 15:48

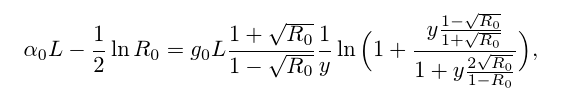
В чём профит? Ответ прост: мне нужно было запрогать нахождение минимума достаточно сложной функции, считать производные этой функции по её параметрам ручкой на бумажке было лень, проверять потом, что я не опечатался при написании кода, и поддерживать этот самый код — лень вдвойне, поэтому было решено написать штуковину, которая это сделает за меня. Ну, чтобы в коде можно было написать что-то такое:

using Formula_t = decltype (k * (_1 - r0) / (_1 + r0) * (g0 / (alpha0 - logr0 / Num<300>) - _1));    // сама формула
const auto residual = Formula_t::Eval (datapoint) - knownValue;    // регрессионный остаток

// производные по параметрам:
const auto dg0 = VarDerivative_t::Eval (datapoint);
const auto dalpha0 = VarDerivative_t::Eval (datapoint);
const auto dk = VarDerivative_t::Eval (datapoint);

Ещё неплохо быть достаточно уверенным, что компилятор это соптимизирует так, как если бы соответствующие производные и функции были написаны руками. А уверенным быть бы хотелось — находить минимум нужно было очень много раз (действительно много, где-то от сотни миллионов до миллиарда, в этом была суть некоего вычислительного эксперимента), поэтому вычисление производных было бы бутылочным горлышком, происходи оно во время выполнения через какую-нибудь рекурсию по древообразной структуре. Если же заставить компилятор вычислять производную, собственно, во время компиляции, то есть шанс, что он по получившемуся коду ещё пройдётся оптимизатором, и мы не потеряем по сравнению с ручным выписыванием всех производных. Шанс реализовался, кстати.

Под катом — небольшое описание, как оно там всё работает.

Начнём с представления функции в программе. Почему-то так получилось, что каждая функция — это тип. Функция — это ещё и дерево выражений, и узел этого дерева представляется типом Node:

template
struct Node;

Здесь NodeClass — тип узла (переменная, число, унарная функция, бинарная функция), Args — параметры этого узла (индекс переменной, значение числа, дочерние узлы).

Узлы умеют себя дифференцировать, печатать и вычислять для данных значений свободных переменных и параметров. Так, если определен тип для представления узла с обычным числом:

using NumberType_t = long long;

template
struct Number {};

template
struct Node>
{
	template
	using Derivative_t = Node>;

	static std::string Print ()
	{
		return std::to_string (N);
	}

	template
	static typename Vec::value_type Eval (const Vec&)
	{
		return N;
	}

	constexpr Node () {}
};

Переменная представляется похожим образом:

template
struct Variable {};

Узел для переменной определяется чуть интереснее, чем для числа:

template
struct Node>
{
	template
	using Derivative_t = std::conditional_t>,
			Node>>;

	static std::string Print ()
	{
		return std::string { Family, '_' } + std::to_string (Index);
	}

	template
	static typename Vec::value_type Eval (const Vec& values)
	{
		return values (Node {});
	}

	constexpr Node () {}
};

Вычисление значения функции, состоящей из одной переменной сводится к её нахождению в словаре значений values, который передаётся в функцию Eval(). Словарь сам умеет находить значение нужной переменной по её типу, поэтому ему мы просто передадим тип нашей переменной и вернём соответствующее значение. Как словарь это делает, мы рассмотрим позже.

С унарными функциями всё становится ещё интереснее.

enum class UnaryFunction
{
	Sin,
	Cos,
	Ln,
	Neg
};

template
struct UnaryFunctionWrapper;

В специализации UnaryFunctionWrapper мы запихнём логику по взятию производных каждой конкретной унарной функции. Чтобы минимально дублировать код, будем брать производную унарной функции по её аргументу, за дальнейшее дифференцирование аргумента по целевой переменной через chain rule будет отвечать вызывающий код:

template<>
struct UnaryFunctionWrapper
{
	template
	using Derivative_t = Node;
};

template<>
struct UnaryFunctionWrapper
{
	template
	using Derivative_t = Node>;
};

template<>
struct UnaryFunctionWrapper
{
	template
	using Derivative_t = Node>, Child>;
};

template<>
struct UnaryFunctionWrapper
{
	template
	using Derivative_t = Node>;
};

Тогда сам узел выглядит следующим образом:

template
struct Node, Node>
{
	using Child_t = Node;

	template
	using Derivative_t = Node::template Derivative_t,
			typename Node::template Derivative_t>;

	static std::string Print ()
	{
		return FunctionName (UF) + "(" + Node::Print () + ")";
	}

	template
	static typename Vec::value_type Eval (const Vec& values)
	{
		const auto child = Child_t::Eval (values);
		return EvalUnary (UnaryFunctionWrapper {}, child);
	}
};

Кстати, отдельную унарную операцию отрицания можно было бы и не вводить, заменив её на умножение на минус единицу.

С бинарными узлами всё аналогично, только производные выглядят совсем страшно. Для деления, например:

template<>
struct BinaryFunctionWrapper
{
	template
	using Derivative_t = Node,
						V
					>,
					Node
						>
					>
				>,
				Node
			>;
};

Тогда искомая метафункция VarDerivative_t определяется довольно просто, ибо по факту лишь вызывает Derivative_t у переданного ей узла:

template
struct VarDerivative;

template
struct VarDerivative>>
{
	using Result_t = typename Expr::template Derivative_t;
};

template
using VarDerivative_t = typename VarDerivative>::Result_t;

Если теперь определить вспомогательные переменные и типы, например:

// алиасы для типов унарных и бинарных функций:
using Sin = UnaryFunctionWrapper;
using Cos = UnaryFunctionWrapper;
using Neg = UnaryFunctionWrapper;
using Ln = UnaryFunctionWrapper;

using Add = BinaryFunctionWrapper;
using Mul = BinaryFunctionWrapper;
using Div = BinaryFunctionWrapper;
using Pow = BinaryFunctionWrapper;

// variable template из C++14 для определения переменной в общем виде:
template
constexpr Node> Var {};

// определим переменную x0 для удобства, авось, ей часто пользоваться будут:
using X0 = Node>;
constexpr X0 x0;
// и так далее для других переменных

// константа для единицы, единица часто встречается в формулах:
constexpr Node> _1;

// перегрузки операторов, им даже не нужно тело, достаточно типа:
template
Node, std::decay_t> operator+ (T1, T2);

template
Node, std::decay_t> operator* (T1, T2);

template
Node, std::decay_t> operator/ (T1, T2);

template
Node, Node>> operator- (T1, T2);

// не совсем операторы, но тоже чтобы удобно писать было:
template
Node> Sin (T);

template
Node> Cos (T);

template
Node> Ln (T);

Что осталось?

Во-первых, разобраться с тем типом, который передаётся в функцию Eval(). Во-вторых, упомянуть про возможность преобразований искомого выражения с заменой одного поддерева на другое. Начнём со второго, оно проще.

Мотивация (можно пропустить): если немного попрофилировать код, который получится с текущей версией, то в глаза бросится, что довольно много времени уходит на вычисление , который, вообще говоря, один и тот же для каждой экспериментальной точки. Не беда! Введём отдельную переменную, которую посчитаем один раз перед расчётом значений нашей формулы на каждой из экспериментальных точек, и заменим все вхождения на эту переменную (собственно, в мотивационном коде в самом начале это уже и сделано). Однако, когда мы будем брать производную по , нам придётся вспомнить, что , вообще говоря, не свободный параметр, а функция от . Вспомнить очень просто: заменим на  (для этого используется метафункция ApplyDependency_t, хотя правильнее было бы её назвать Rewrite_t или вроде того), продифференцируем, вернём на  обратно:

using Unwrapped_t = ApplyDependency_t;
using Derivative_t = VarDerivative_t;
using CacheLog_t = ApplyDependency_t;

Реализация многословна, но идейно проста. Рекурсивно спускаемся по дереву формулы, подменяя элемент дерева, если он в точности совпадает с шаблоном, иначе ничего не меняем. Итого три специализации: для спуска по дочернему узлу унарной функции, для спуска по дочерним узлам бинарной функции, и собственно для замены, при этом специализации для спуска по дочерним узлам должны проверять, что шаблон не совпадает с поддеревом, соответствующим рассматриваемой подфункции:

template
struct ApplyDependency
{
	using Result_t = Formula;
};

template
using ApplyDependency_t = typename ApplyDependency, std::decay_t, Formula>::Result_t;

template
struct ApplyDependency, Child>,
		std::enable_if_t, Child>>::value>>
{
	using Result_t = Node<
				UnaryFunctionWrapper,
				ApplyDependency_t
			>;
};

template
struct ApplyDependency, FirstNode, SecondNode>,
		std::enable_if_t, FirstNode, SecondNode>>::value>>
{
	using Result_t = Node<
				BinaryFunctionWrapper,
				ApplyDependency_t,
				ApplyDependency_t
			>;
};

template
struct ApplyDependency
{
	using Result_t = Expr;
};

Ффух. Осталось разобраться с передачей значений параметров.

Вспомним, что каждый параметр имеет свой собственный тип, поэтому если мы построим семейство функций, перегруженных по типу параметров, каждая из которых возвращает соответствующее значение, то снова (прямо как с вычислением унарных функций чуть ранее) есть шанс, что компилятор это дело свернёт и соптимизирует (а он, кстати, и соптимизирует, умница такой). Ну, что-то вроде

auto GetValue (Variable<'x', 0>)
{
    return value_for_x0;
}

auto GetValue (Variable<'x', 1>)
{
    return value_for_x1;
}

...

Только мы хотим сделать это красиво, чтобы можно было написать, например:

BuildFunctor (g0, someValue,
        alpha0, anotherValue,
        k, yetOneMoreValue,
        r0, independentVariable,
        logr0, logOfTheIndependentVariable);

Как мы можем скрестить ужа и ежа, сделав в общем виде функцию, тип параметра которой задаётся в компил-тайме, а значение — в рантайме? Лямбды спешат на помощь!

template
auto BuildFunctor (NodeType, ValueType val)
{
    return [val] (NodeType) { return val; };
}

Пусть у нас есть две таких функции, как мы можем получить семейство функций в одном пространстве имён, чтобы нужная выбиралась перегрузкой? Наследование спешит на помощь!

template
struct Map : F, S
{
	using F::operator();
	using S::operator();

	Map (F f, S s)
	: F { std::forward (f) }
	, S { std::forward (s) }
	{
	}
};

template
auto Augment (F&& f)
{
	return f;
}

template
auto Augment (F&& f, S&& s)
{
	return Map, std::decay_t> { f, s };
}

template
auto BuildFunctor ()
{
	struct
	{
		ValueType operator() () const
		{
			return {};
		}

		using value_type = ValueType;
	} dummy;
	return dummy;
}

template
auto BuildFunctor (NodeType, ValueType val, Tail&&... tail)
{
	return detail::Augment ([val] (NodeType) { return val; },
			BuildFunctor (std::forward (tail)...));
}