Аналитическое решение уравнений Максвелла: собственные моды оптоволокна (любителям «матана»)12.04.2017 08:39

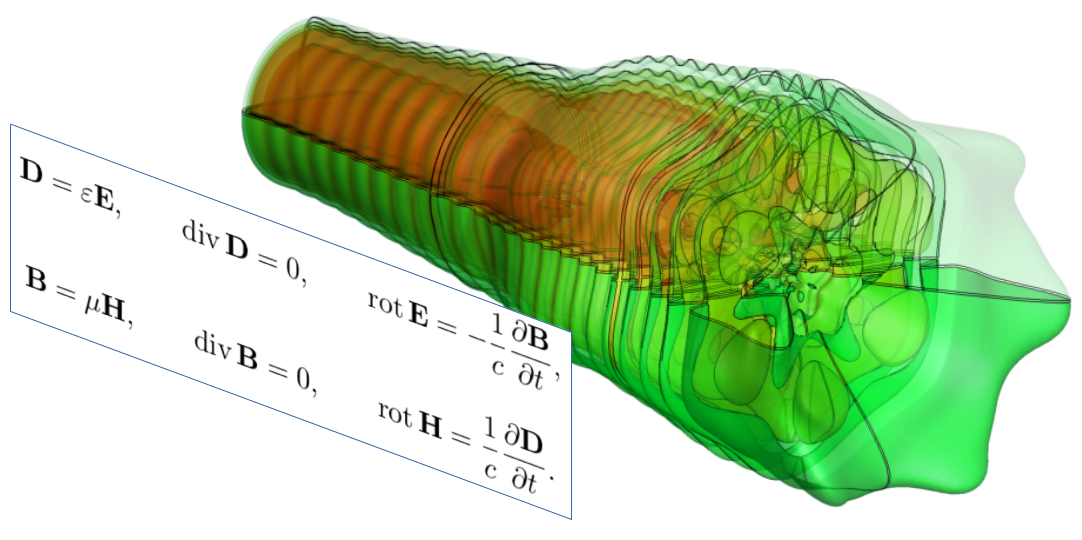
Как-то мне понадобилась »собственная мода оптоволокна». Но я нигде не нашел аналитического выражения электромагнитного поля. Ну и «сделал сам», раз не нашел, и оформил для всех тут, в статье. Так что, скорее всего, нигде больше вы такого не встретите — уникальнейшая вещь! В книжках это не пишут, потому что оно длинное — обычно пишут самое простое, а про общий случай упоминают вскользь. Ну вот он, общий случай, под катом.

Решить уравнения Максвелла с условиями:
— оптоволокно состоит из сердцевины радиуса $a$ с диэлектрической проницаемостью $\varepsilon_1$ и оболочки бесконечного внешнего радиуса с диэлектрической проницаемостью $\varepsilon_2$ ,
— поле периодично по $z$ , пространственная частота всех компонент поля едина: $k_z$ ,
— компоненты поля на оси $O_z$ — без особенностей,
— компоненты поля при $r \rightarrow\infty$ интегрируемы с квадратом,
— тангенциальные компоненты поля на поверхности цилиндра $r=a$ — непрерывны:

$E_{z,1}\bigg|_{r=a}=E_{z,2}\bigg|_{r=a},$

$E_{\varphi,1}\bigg|_{r=a}=E_{\varphi,2}\bigg|_{r=a},$

$H_{z,1}\bigg|_{r=a}=H_{z,2}\bigg|_{r=a},$

$H_{\varphi,1}\bigg|_{r=a}=H_{\varphi,2}\bigg|_{r=a}$

Подставив в уравнения Максвелла периодическую зависимость по $z$ :

$\textbf{E}(x,y,z,t) = \left( \begin{array}{c} e_x(x,y)\\ e_y(x,y)\\ e_z(x,y) \end{array} \right) \exp\left\lbrace ik_zz - i\omega t \right\rbrace, \quad \textbf{B}(x,y,z,t) = \left( \begin{array}{c} b_x(x,y)\\ b_y(x,y)\\ b_z(x,y) \end{array} \right) \exp\left\lbrace ik_zz - i\omega t \right\rbrace,$

получаются уравнения на $z$ -компоненты поля:

$\Delta_{\bot}e_z + \gamma^2e_z=0,\,\Delta_{\bot}b_z + \gamma^2b_z=0,\,\text{где }\Delta_{\bot}=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2},\quad \gamma^2 = \varepsilon\mu\frac{\omega^2}{c^2}-k^2_z.$

При этом остальные компоненты выражаются через $z$ -компоненты по закону:

$\textbf{b}_{\bot} = \frac{i}{\gamma^2}\left\lbrace k_z \operatorname{grad}_{\bot}b_z + \varepsilon\mu\frac{\omega}{c}\left[ \hat{\textbf{z}}\times\operatorname{grad}_{\bot}e_z\right] \right\rbrace, \, \textbf{e}_{\bot} = \frac{i}{\gamma^2}\left\lbrace k_z \operatorname{grad}_{\bot}e_z - \frac{\omega}{c}\left[ \hat{\textbf{z}}\times\operatorname{grad}_{\bot}b_z\right] \right\rbrace,$

где $\hat{\textbf{z}}$ — единичный вектор вдоль оси $O_z$ , $\operatorname{grad}_{\bot} = \hat{\textbf{x}} \partial_x+\hat{\textbf{y}}\partial_y$ , $\textbf{e}_{\bot} = \hat{\textbf{x}}e_x + \hat{\textbf{y}} e_y,\,\textbf{b}_{\bot} = \hat{\textbf{x}}b_x +\hat{\textbf{y}}b_y$ .

Уравнения на $e_z,\,b_z$ имеют один вид, решения одинаковы, поэтому естественно переобозначение искомой функции:

$\Delta_{\bot}\psi + \gamma^2\psi=0.$

В полярных координатах уравнение имеет вид:

$r^2\frac{\partial^2}{\partial r^2}\psi + r\frac{\partial}{\partial r}\psi + \frac{\partial^2 }{\partial \varphi^2}\psi + r^2\left( \frac{\varepsilon\mu}{c^2}\omega^2 - k_z^2 \right) \psi = 0.$

Подстановкой в уравнение зависимости $\psi(r,\varphi) = u(r)v(\varphi)$ переменные разделяются:

$\frac{1}{u(r)}r^2\frac{\partial^2}{\partial r^2}u(r) + \frac{1}{u(r)}r\frac{\partial}{\partial r}u(r) + r^2\left( \frac{\varepsilon\mu}{c^2}\omega^2 - k_z^2 \right) = - \frac{1}{v(\varphi)}\frac{\partial^2 }{\partial \varphi^2}v(\varphi).$

Обозначив константу равенства символом $\nu^2$ выписываются обе части равенства:

$$display$$- \frac{1}{v (\varphi)}\frac{\partial^2 }{\partial \varphi^2}v (\varphi) = \nu^2,$$display$$

$\frac{1}{u(r)}r^2\frac{\partial^2}{\partial r^2}u(r) + \frac{1}{u(r)}r\frac{\partial}{\partial r}u(r) + r^2\left( \frac{\varepsilon\mu}{c^2}\omega^2 - k_z^2 \right) = \nu^2.$

Первое уравнение имеет решения: $v = С_1\exp\left\lbrace i\nu \varphi \right\rbrace$ .

Из периодического граничного условия $v(\varphi)=v(\varphi+2\pi)$ , следует, что $\nu$ — целое: $\exp\left\lbrace i\nu \varphi \right\rbrace=\exp\left\lbrace i\nu (\varphi+2\pi) \right\rbrace\rightarrow 1=\exp\left\lbrace i\nu2\pi \right\rbrace = \cos(2\pi\nu)+ i\sin(2\pi\nu) \Rightarrow$ $\Rightarrow\cos(2\pi\nu)=1, \sin(2\pi\nu)=0 \Rightarrow \nu =\ldots -2,-1,0,1,2\ldots$

Второе уравнение сводится либо к уравнению Бесселя, либо к модифицированному уравнению Бесселя:
1. Уравнение Бесселя:

$\rho_1^2\frac{d^2u}{d\rho_1^2} + \rho_1\frac{du}{d\rho_1} + (\rho_1^2 - \nu^2)u = 0,\text{ при }\rho_1 = r \sqrt{ \frac{\varepsilon_1\mu}{c^2}\omega^2 - k_z^2 },$

2. Модифицированное уравнение Бесселя:

$\rho_2^2\frac{d^2u}{d\rho_2^2} + \rho_2\frac{du}{d\rho_2} - (\rho_2^2 + \nu^2)u = 0,\text{ при }\rho_2 = r \sqrt{ k_z^2 - \frac{\varepsilon_2\mu}{c^2}\omega^2 }.$

Уравнению Бесселя удовлетворяют функции Бесселя $J_{\nu}(\rho_1)$ и функции Неймана $Y_{\nu}(\rho_1)$ . Модифицированному уравнению Бесселя удовлетворяют функции Инфельда $I_{\nu}(\rho_2)$ и функции Макдональда $K_{\nu}(\rho_2)$ .

В силу граничных условий: при $r=0$ — функция без особенностей, при $r=\infty$ — функция интегрируема с квадратом, при $r=a$ — тангенциальные компоненты поля непрерывны, — в качестве решения предлагается следующая комбинация: при $r < a$ — функция Бесселя $J_{\nu}(\rho_1)$ , при $r > a$» /> — функция Макдональда <img src= .

Из предложенной комбинации следует, что сердцевина должна быть более оптически плотной, чем оболочка, $$\varepsilon_1 > \varepsilon_2$» />: <img src=$ компоненты $e_z,\,b_z$ записываются в виде:

$e_{z,1} = A_eJ_{|\nu|}(\gamma r)\exp\left\lbrace i\nu \varphi \right\rbrace,\text{ при }r<a,$

$$e_{z,2} = B_eK_{|\nu|}(\kappa r)\exp\left\lbrace i\nu \varphi \right\rbrace,\text{ при }r>a,$» /> <img src=$

$$b_{z,2} = B_bK_{|\nu|}(\kappa r)\exp\left\lbrace i\nu \varphi \right\rbrace,\text{ при }r>a. $» /> Здесь полагается, что <img src=$ (может принимать отрицательные значения), потому в индексах функций присутствует знак модуля (в уравнении Бесселя имеет место $\nu^2$ , знак индекса предполагается неотрицательный). Далее знак модуля в индексах функций опускается, но подразумевается.

Кроме того, введен индекс для магнитной проницаемости: $\mu_1$ — в сердцевине, $\mu_2$ — в оболочке.

Используя закон

находятся компоненты $e_{\varphi,1},\,e_{\varphi,2},\,h_{\varphi,1},\,h_{\varphi,2}$ , имея при этом в виду, что $\textbf{h}=\textbf{b}/\mu$ .
Компоненты подставляются в граничное условие непрерывности тангенциальных компонент:

$e_{z,1}\bigg|_{r=a}=e_{z,2}\bigg|_{r=a},$

$e_{\varphi,1}\bigg|_{r=a}=e_{\varphi,2}\bigg|_{r=a},$

$h_{z,1}\bigg|_{r=a}=h_{z,2}\bigg|_{r=a},$

$h_{\varphi,1}\bigg|_{r=a}=h_{\varphi,2}\bigg|_{r=a}.$

Получается система линейных уравнений, суть соотношения на константы $A_e,\,A_b,\,B_e,\,B_b$ , которая имеет вид:

$\left( \begin{array}{cccc} J_{\nu}(\gamma a) & -K_{\nu}(\kappa a) & 0 & 0 \\ 0 & 0 & \frac{1}{\mu_1}J_{\nu}(\gamma a) & -\frac{1}{\mu_2}K_{\nu}(\kappa a) \\ \frac{\nu k_z}{a\gamma^2} J_{\nu}(\gamma a) & \frac{\nu k_z}{a\kappa^2} K_{\nu}(\kappa a) & \frac{i}{\gamma^2}\frac{\omega}{c}\gamma J^{\prime}_{\nu}(\gamma a) & \frac{i}{\kappa^2} \frac{\omega}{c} \kappa K^{\prime}_{\nu}(\kappa a) \\ i\frac{\varepsilon\mu}{\gamma^2\mu_1}\frac{\omega}{c}\gamma J^{\prime}_{\nu}(\gamma a) & \frac{i}{\mu_2\kappa^2}\varepsilon\mu\frac{\omega}{c}\kappa K^{\prime}_{\nu}(\kappa a) & -\frac{k_z \nu}{a\gamma^2 \mu_1} J_{\nu}(\gamma a) & - \frac{\nu k_z}{\mu_2a\kappa^2}K_{\nu}(\kappa a) \end{array} \right) \left( \begin{array}{c} A_e\\ B_e\\ A_b\\ B_b \end{array} \right) = 0,$

Для существования нетривиального решения системы линейных уравнений, определитель матрицы должен равняться нулю:

$\left( \frac{\varepsilon_1\mu_1}{x^2}+\frac{\varepsilon_2\mu_2}{y^2}\right) \left( \frac{1}{x^2} + \frac{1}{y^2}\right)\nu^2 = \left[ \mu_2 g(y)+\mu_1 f(x)\right] \left[ \varepsilon_2g(y) + \varepsilon_1 f(x)\right] .$

В этой записи нулевого детерминанта использованы обозначения: $f(x) = \frac{J^{\prime}_{\nu}(x)}{xJ_{\nu}(x)}, \, g(y) = \frac{K^{\prime}_{\nu}(y)}{yK_{\nu}(y)},$ $x=\gamma a,\,y=\kappa a$ и соотношения: $\frac{\omega^2}{c^2} = \frac{\kappa^2+\gamma^2}{\varepsilon_1\mu_1 - \varepsilon_2\mu_2},\,k_z^2 = \frac{\varepsilon_1\mu_1\kappa^2+\varepsilon_2\mu_2\gamma^2}{\varepsilon_1\mu_1 - \varepsilon_2\mu_2}$ , которые следуют из введенных ранее определений: $\gamma^2 = \frac{\varepsilon_1\mu_1}{c^2}\omega^2 - k_z^2, \, \kappa^2 = k_z^2 - \frac{\varepsilon_2\mu_2}{c^2}\omega^2$ .

Величины $x,\,y$ — связаны еще одним равенством, следующим из двух последних определений и утверждения, что $k_z$ — едина для всех компонент:

$x^2+y^2 = (\varepsilon_1\mu_1 - \varepsilon_2\mu_2)a^2\frac{\omega^2}{c^2}.$

Для нахождения $x,\,y$ из системы уравнений:

$x^2+y^2 = (\varepsilon_1\mu_1 - \varepsilon_2\mu_2)a^2\frac{\omega^2}{c^2},$

необходимо задать: $\nu,\,\omega,\,\varepsilon_1,\,\mu_1,\,\varepsilon_2,\,\mu_2,\,a$ .

Связь $x$ и $y$ первым уравнением представляет собой серию линий на плоскости (граница раздела между синим и красным цветами, см. рис. ниже). Характер линий зависит от $\nu$ .

Связь $x$ и $y$ вторым уравнением представляет собой окружность с радиусом, линейно зависящим от $a$ . Точки пересечения линий являются решениями системы уравнений.

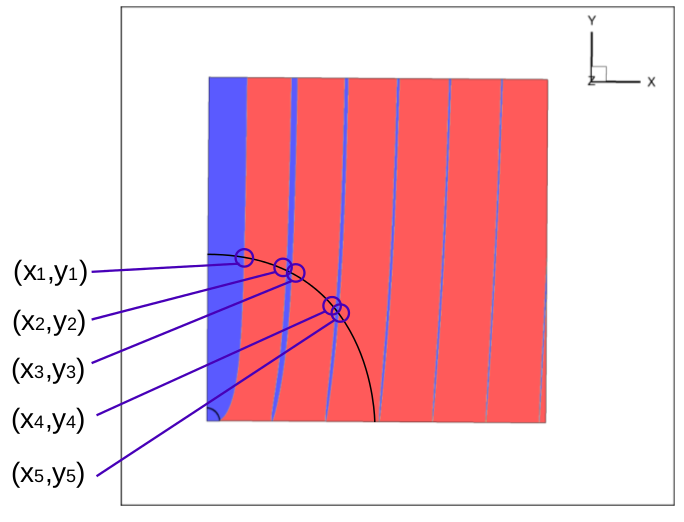
Набор решений составляет конечное число пар чисел $(x_i,y_i)$ . Каждой такой паре чисел соответствует конфигурация электромагнитного поля, называемой «собственной модой».

Моду оптоволокна принято обозначать следующим образом: две буквы ( $E,\,H$ ) — на первом месте буква с наибольшей $z$ -компонентой и два индекса: на первом месте $\nu$ , на втором номер ветви (на рисунке обозначена синим цветом).

Примеры обозначения:
$HE_{11}$ говорит о том, что $H_z$ больше, чем $E_z$ , $\nu=1$ , выбрана пара (см.рис. выше) $(x_1,y_1)$ ,
$EH_{13}$ говорит о том, что $E_z$ больше, чем $H_z$ , $\nu=1$ , выбрана пара (см.рис. выше) $(x_5,y_5)$ (третья синяя ветвь).

Подготовительные вычисления:

01. Задать $\nu,\,\omega,\,\varepsilon_1,\,\mu_1,\,\varepsilon_2,\,\mu_2,\,a$ ;
02. Найти наборы $(x,y)$ , выбрать один, (п.9);
03. Вычислить $k_z,\,\gamma,\,\kappa$ , (п.8);
04. Вычислить $A_e,\,A_b,\,B_e,\,B_b$ , (п.7).

Выражения в цилиндрических координатах компонент поля:

$e_z = A_eJ_{\nu}(\gamma r)\exp\left\lbrace i\nu \varphi \right\rbrace,\text{ при }r<a,$

$$e_z = B_eK_{\nu}(\kappa r)\exp\left\lbrace i\nu \varphi \right\rbrace,\text{ при }r>a, $» /> <img src=$

$$b_z = B_bK_{\nu}(\kappa r)\exp\left\lbrace i\nu \varphi \right\rbrace,\text{ при }r>a. $» /> Далее, при <img src=$ :

$\left( \begin{array}{c} b_r\\ b_{\varphi} \end{array} \right) = \frac{i}{\gamma^2}\left\lbrace k_z \left( \begin{array}{c} A_b \gamma J^{\prime}_{\nu}(\gamma r) \\ \frac{1}{r} i \nu A_b J_{\nu}(\gamma r) \end{array} \right) + \varepsilon\mu\frac{\omega}{c} \left( \begin{array}{c} -\frac{1}{r} i\nu A_e J_{\nu}(\gamma r)\\ A_e \gamma J^{\prime}_{\nu}(\gamma r) \end{array} \right) \right\rbrace \exp(i\nu \varphi) ,$

$\left( \begin{array}{c} e_r\\ e_{\varphi} \end{array} \right) = \frac{i}{\gamma^2}\left\lbrace k_z \left( \begin{array}{c} A_e \gamma J^{\prime}_{\nu}(\gamma r)\\ \frac{1}{r} i\nu A_e J_{\nu}(\gamma r) \end{array} \right) - \frac{\omega}{c} \left( \begin{array}{c} -\frac{1}{r}A_b i\nu J_{\nu}(\gamma r)\\ A_b \gamma J^{\prime}_{\nu}(\gamma r) \end{array} \right) \right\rbrace \exp(i\nu \varphi).$

При $r > a$» />:


<img src=

$\left( \begin{array}{c} e_r\\ e_{\varphi} \end{array} \right) = -\frac{i}{\kappa^2}\left\lbrace k_z \left( \begin{array}{c} B_e \kappa K^{\prime}_{\nu}(\kappa r)\\ \frac{1}{r} i\nu B_e K_{\nu}(\kappa r) \end{array} \right) - \frac{\omega}{c} \left( \begin{array}{c} -\frac{1}{r}B_b i\nu K_{\nu}(\kappa r)\\ B_b \kappa K^{\prime}_{\nu}(\kappa r) \end{array} \right) \right\rbrace \exp(i\nu \varphi).$

$\textbf{E}(x,y,z,t) = \left( \begin{array}{c} e_r(x,y)\\ e_{\varphi}(x,y)\\ e_z(x,y) \end{array} \right) \exp\left\lbrace ik_zz - i\omega t \right\rbrace, \quad \textbf{B}(x,y,z,t) = \left( \begin{array}{c} b_r(x,y)\\ b_{\varphi}(x,y)\\ b_z(x,y) \end{array} \right) \exp\left\lbrace ik_zz - i\omega t \right\rbrace.$

При этом замыкающие соотношения стандартные: $\textbf{D}=\varepsilon_{1,2} \textbf{E},\, \textbf{B}= \mu_{1,2} \textbf{H}$ (индексы указывают на соответствующие среды).

Выражение поля в декартовой системе координат через цилиндрические для электрических компонент:

$\left( \begin{array}{c} E_x\\ E_y\\ E_z \end{array} \right) = \left( \begin{array}{ccc} \cos\varphi & -\sin\varphi & 0\\ \sin\varphi & \cos\varphi & 0\\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} E_r\\ E_{\varphi}\\ E_z \end{array} \right).$

Для магнитных компонент матрица та же.

Выбирая $a$ можно добиться единственности решения:

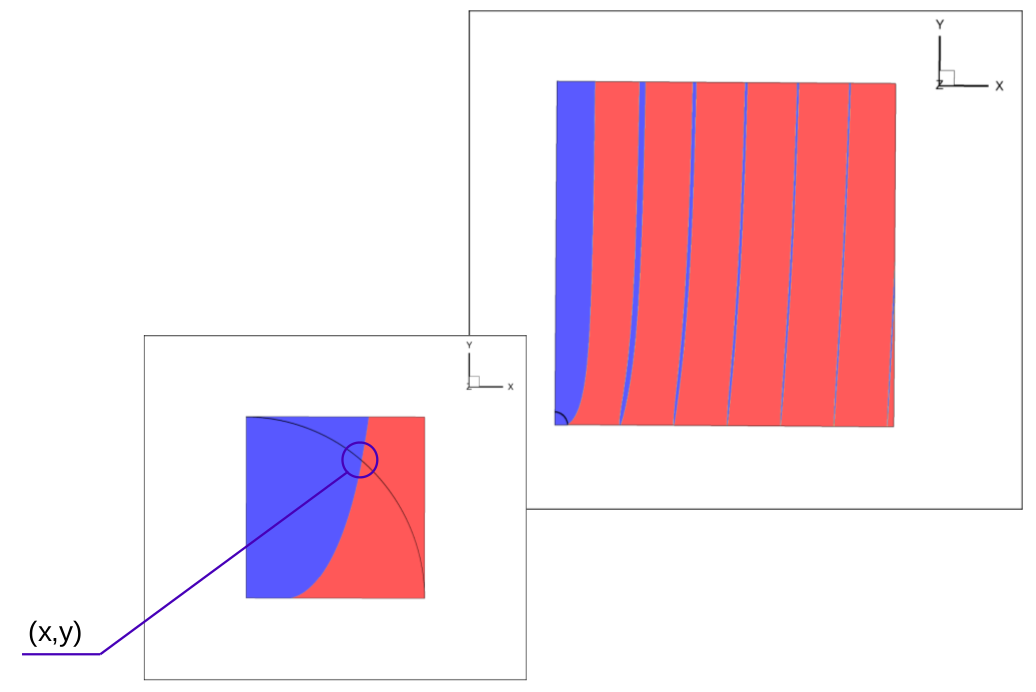
Такое оптоволокно называется одномодовым. Однако следует заметить, что «одномодовость» зависит от частоты — более высокие частоты распространяются в «одномодовом» волокне в виде набора мод.

Иногда говорят о сохранении поляризации в оптоволокне, имея в виду перпендикулярные компоненты поля моды $HE_{11}$ : векторы компонент поля в плоскости практически соправлены. Однако, общая картина вращается во времени (см. видео ниже), — о сохранении поляризации в таком оптоволокне говорить не приходится.

[embedded content]

Для интереса ниже показана эволюция в течении временного периода моды $HE_{11}$

[embedded content]

и моды $HE_{31}$

[embedded content]