Алгоритмы компрессии данных: принципы и эффективность03.07.2023 19:17

Автор статьи: Артем Михайлов

В современном информационном обществе объем данных стремительно растет, и с каждым годом все больше информации генерируется и обрабатывается. В связи с этим, важным аспектом стало умение эффективно управлять данными, чтобы не только сохранить информацию, но и оптимизировать ее использование и передачу. Одним из основных инструментов для достижения этой цели является компрессия данных.

Компрессия данных — это процесс сокращения объема данных без потерь или с минимальной потерей информации. Путем применения алгоритмов и методов компрессии, мы можем существенно уменьшить размер данных, сохраняя при этом их суть и основные характеристики. Это может быть полезно во множестве ситуаций, начиная от экономии места на хранилище и ускорения передачи данных до минимизации затрат на интернет-трафик и повышения производительности систем обработки и анализа информации.

Главная цель алгоритмов компрессии данных — уменьшить размер данных, сохраняя при этом их информационную значимость. Компрессия данных активно применяется во множестве областей, включая сжатие аудио и видеофайлов, сжатие изображений, архивирование файлов и многое другое.

В аудио и видео сжатие позволяет свести к минимуму размер файлов, необходимых для их хранения и передачи онлайн. Это особенно актуально для стриминговых платформ и мессенджеров, где важно обеспечить высокое качество воспроизведения при минимальных затратах на трафик.

Сжатие изображений играет важную роль в сфере визуального контента, где быстродействие и отображение графических элементов на различных устройствах имеют первостепенное значение. Благодаря алгоритмам сжатия данных, изображения могут быть оптимизированы для различных ос и экранов, минимизируя размер файлов без потери качества визуального отображения.

Архивирование файлов также является важным аспектом компрессии данных. Благодаря сжатию, мы можем упаковывать несколько файлов в один архив и таким образом сэкономить место на хранилище или сократить время передачи данных.

Однако, важно понимать, что каждый алгоритм компрессии имеет свои особенности и область применения. В данной статье мы рассмотрим различные алгоритмы компрессии данных и их преимущества в разных сферах, а также обсудим некоторые основные принципы, на которых они основаны.

Основные принципы алгоритмов компрессии данных

Рассмотрим основные принципы алгоритмов компрессии данных.

1. Удаление избыточности

Первый принцип компрессии данных заключается в удалении избыточности. Избыточность включает повторяющиеся данные и линейные зависимости. Повторяющиеся данные возникают, когда одна и та же информация появляется несколько раз. Для удаления повторяющихся данных, можно использовать методы, такие как метод Лемпеля-Зива-Велча или алгоритм RLE (Run-Length Encoding).

Линейные зависимости возникают, когда одна последовательность данных может быть представлена в виде линейной комбинации других последовательностей данных. Такие зависимости можно использовать для сжатия информации. Например, в методе предсказательного алгоритма сжатия данных, используется линейная зависимость между предыдущими данными и текущими данными для определения оптимального представления текущих данных.

2. Замена данных более короткими представлениями

Второй принцип компрессии данных заключается в замене данных более короткими представлениями. Это включает использование словарей и замену символов и символьных последовательностей.

Использование словарей является эффективным способом сжатия данных, особенно когда в данных присутствует много повторений. Словарь содержит набор уникальных символьных или более длинных последовательностей данных и их соответствующих сокращенных кодов. При сжатии данных, заменяются повторяющиеся символьные или последовательностей данных их кодами из словаря.

Замена символов и символьных последовательностей основывается на частотности их появления. Часто используемые символы или последовательности заменяются более короткими кодами, тогда как редкие символы или последовательности заменяются более длинными кодами. Для определения оптимальных замен используется алгоритм Хаффмана или алгоритм адаптивного арифметического кодирования.

3. Использование арифметического кодирования

Арифметическое кодирование — это принцип компрессии данных, основанный на представлении всего входного потока данных одним числом, попадающим в определенный интервал. В арифметическом кодировании, каждому символу или символьной последовательности присваивается определенный интервал вещественных чисел, пропорционально их вероятности. При декодировании, входной поток делят на интервалы, каждый из которых соответствует символу или символьной последовательности, восстанавливая исходные данные.

4. Использование сжатия с потерями

Последний принцип компрессии данных — использование сжатия с потерями. В некоторых случаях, возможна потеря некоторого качества данных, но при этом можно достичь более высокой степени сжатия. Примерами алгоритмов сжатия с потерями являются алгоритмы JPEG для сжатия изображений и алгоритм MP3 для сжатия аудио.

Виды алгоритмов компрессии данных

Одним из важных аспектов компрессии данных является выбор алгоритма, который будет применен для этой цели. рассмотрим две основные категории алгоритмов компрессии данных: алгоритмы без потерь и алгоритмы с потерями.

Без потерь
Алгоритмы компрессии данных без потерь предназначены для сокращения объема данных без изменения их содержимого. Они основываются на поиске и использовании закономерностей и повторяющихся структур в данных.

1. Алгоритм Хаффмана
Алгоритм Хаффмана является одним из наиболее известных и широко используемых алгоритмов компрессии данных без потерь. Он был разработан Дэвидом Хаффманом в 1952 году и стал мощным инструментом для сжатия текстовых данных, а также других типов данных с неравномерным распределением символов.

Алгоритм основывается на построении оптимального префиксного кода для каждого символа в исходных данных. Префиксный код представляет собой такую систему кодирования, где для каждого символа нет никакого кодового слова, являющегося префиксом другого кодового слова. Такое свойство кода позволяет эффективно сжимать данные без потери информации при декодировании.

Алгоритм Хаффмана начинается с подсчета частоты встречаемости каждого символа в исходных данных. Затем эти частоты используются для строительства дерева Хаффмана. Дерево Хаффмана представляет собой двоичное дерево, где каждый узел содержит символ и его частоту, а листья представляют отдельные символы.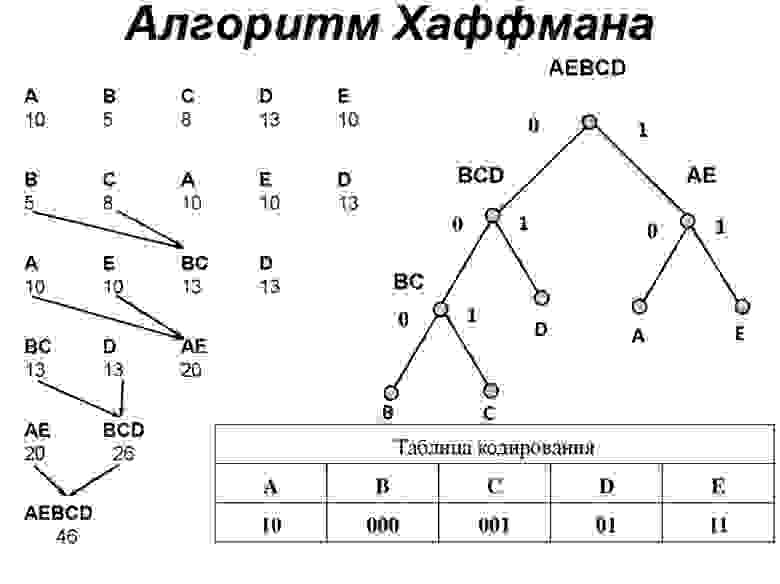

В процессе построения дерева Хаффмана, символы сочетаются вместе с их частотами и объединяются в новый узел. Новый узел имеет суммарную частоту двух объединяемых символов и не имеет явного символа. Этот процесс повторяется до тех пор, пока все символы не объединятся в одном корневом узле дерева.

После построения дерева Хаффмана, каждый символ получает свой префиксный код, пройдя по соответствующему пути от корня до листа. Путь к левому наследнику представляет »0», а путь к правому наследнику — »1». Таким образом, получается кодирование каждого символа без возможности двусмысленности декодирования.

Получив префиксные коды для всех символов, данные кодируются путем замены каждого символа его кодовым словом. Полученный код является результатом сжатия данных алгоритмом Хаффмана. При декодировании, эти кодовые слова снова преобразуются в исходные символы, используя дерево Хаффмана.

Преимуществами алгоритма Хаффмана являются его простота и эффективность сжатия для данных с неравномерным распределением символов. Он широко применяется в различных областях, включая сжатие текстовых данных, аудиофайлов и изображений.

2. Алгоритм Лемпеля-Зива-Велча (LZW)
Алгоритм Лемпеля-Зива-Велча (LZW) является еще одним важным алгоритмом компрессии данных без потерь. Он был разработан Абрахамом Лемпелем и Яаковом Зивом в 1977 году, а позже его улучшенная версия была предложена Терри Велчем.

LZW основывается на идее построения словаря, состоящего из уже встреченных входных данных строк. Он начинает с инициализации словаря базовыми символами, такими как отдельные символы или короткие строки. Затем LZW сканирует входные данные и сравнивает текущую строку с существующими элементами словаря.

Если текущая строка уже присутствует в словаре, LZW переходит к следующему символу и повторяет процесс. Если текущая строка не найдена в словаре, LZW добавляет ее в словарь и заменяет текущую строку ссылкой на предыдущий подходящий элемент словаря. Это позволяет уменьшить объем данных, заменяя повторяющиеся последовательности более короткими ссылками.

LZW продолжает сканирование и построение словаря до тех пор, пока не достигнет конца входных данных или до достижения заданного предела словаря. Затем полученные ссылки и окончательный словарь используются для восстановления исходных данных при декомпрессии.

При сжатии данных алгоритм LZW эффективно удаляет повторяющиеся участки информации и заменяет их более компактными ссылками. Благодаря этому, объем данных значительно сокращается без потери информации. Однако для корректной декомпрессии необходимо сохранить информацию о словаре или использовать специальные механизмы, позволяющие восстановить исходный словарь при декомпрессии.

Алгоритм LZW широко применяется для сжатия текстовых данных, а также в других областях, где встречается неравномерное распределение символов или повторяющиеся структуры данных. Он обладает высоким уровнем сжатия и высокой скоростью выполнения, что делает его особенно полезным для решения задач сжатия данных без потерь.

С потерями
Алгоритмы компрессии данных с потерями используются в случаях, когда незначительная потеря некоторой информации может быть допустима для достижения более значительного сжатия данных. Такие алгоритмы широко применяются в областях, где важна экономия пространства, например, в мультимедиа и аудио-видео сжатии.

1. JPEG
Алгоритм компрессии JPEG (Joint Photographic Experts Group) является одним из самых широко используемых алгоритмов с потерями для сжатия изображений. JPEG был разработан группой специалистов в области фотографии и изображений в 1986 году и стал международным стандартом.

Основная идея алгоритма JPEG заключается в разделении изображения на частоты и квантование каждой из них. Алгоритм использует преобразование косинусного ряда (DCT) для перевода пространственного представления изображения в частотное представление. Преобразование DCT представляет каждый блок пикселей изображения амплитуды различных частотных компонент, от наиболее низких частот до наиболее высоких.

После выполнения DCT каждый блок пикселей подвергается квантованию, что позволяет удалить менее значимые частоты с большей точностью. Он основан на разделении блоков на квантовых таблицах, где каждая таблица предоставляет величину кванта для соответствующих частотных компонент. Более низкие таблицы имеют больший квант и могут значительно снизить поток данных, тогда как более высокие таблицы имеют меньший квант и сохраняют больше деталей.

После этапа квантования, данные проходят через последовательное применение кодирования Хаффмана для дальнейшего уменьшения размера файла. Кодирование Хаффмана основано на использовании более коротких кодов для более частых символов и длинных кодов для редких символов, что позволяет достичь эффективного сжатия.

Хотя алгоритм JPEG с «потерями», он дает возможность установить параметр качества, который определяет степень потерь информации. Чем выше качество, тем меньше потерь, но и размер файла остается большим, а чем ниже качество, тем больше потерь, но файл становится меньше.

JPEG является основным форматом сжатия для фотографий и изображений на веб-страницах, в цифровых фотоаппаратах, мобильных устройствах и других средствах хранения и передачи изображений.

2. MP3
Алгоритм компрессии MP3 используется для сжатия аудиофайлов с потерями. Он работает на основе психоакустической модели, которая анализирует свойства звуковых сигналов и их восприятия человеком. Затем, используя эту информацию, алгоритм удаляет малозаметные компоненты аудиофайла, которые субъективно не воспринимаются человеком. В результате этого, размер аудиофайла существенно сокращается без ухудшения качества звучания воспроизведения.

Оценка эффективности алгоритмов компрессии данных

В наше время, когда объемы данных растут с неимоверной скоростью, возникает острая необходимость в эффективных методах сжатия информации. Коэффициент сжатия является одним из главных параметров, определяющих эффективность алгоритмов компрессии данных. В этом разделе мы рассмотрим его определение и расчет, а также проведем сравнительный анализ различных алгоритмов сжатия.

Коэффициент сжатия

1. Определение и расчет

Коэффициент сжатия — это показатель, отражающий степень уменьшения объема данных после применения алгоритма сжатия. Он вычисляется как отношение исходного объема данных к объему данных после сжатия и измеряется в процентах или в коэффициентах.

Формула для расчета коэффициента сжатия выглядит следующим образом:
Коэффициент сжатия = (Исходный объем данных - Объем данных после сжатия) / Исходный объем данных

Пример:
Предположим, что у нас есть файл размером 10 МБ (мегабайт) и после сжатия его размер уменьшился до 2 МБ. Тогда коэффициент сжатия можно рассчитать следующим образом:
Коэффициент сжатия = (10 — 2) / 10 = 0.8 или 80%

2. Сравнение различных алгоритмов

Важным этапом при выборе алгоритма сжатия данных является сравнительный анализ их эффективности. В данном случае, наиболее важным фактором является коэффициент сжатия, который позволяет оценить, насколько успешно каждый алгоритм уменьшает объем данных.

Примеры алгоритмов сжатия данных и их коэффициенты сжатия:

— Алгоритм A: Коэффициент сжатия — 0.9 или 90%
— Алгоритм B: Коэффициент сжатия — 0.7 или 70%
— Алгоритм C: Коэффициент сжатия — 0.85 или 85%.

Из приведенных примеров видно, что алгоритм A обладает лучшей эффективностью сжатия, поскольку он уменьшил размер данных на 90%. Однако, выбор алгоритма сжатия должен основываться на различных факторах, включая не только коэффициент сжатия, но и время, требуемое для сжатия и распаковки данных, а также требования по сохранению качества.

Потери качества при сжатии с потерями

1. Виды потерь качества

Сжатие данных с потерями является одним из основных подходов к сжатию информации. При этом происходит потеря некоторой части исходных данных, что может привести к снижению качества воспроизведения. Однако, в некоторых случаях потери качества незначительны и поэтому такой тип компрессии широко применяется.

Виды потерь качества при сжатии с потерями:
— Потеря детализации: при сжатии изображения, некоторые детали могут быть потеряны, что может привести к размытию изображения.
— Потеря точности: при сжатии числовых данных, точность значения может быть снижена, что может вызвать незначительные погрешности при восстановлении данных.
— Потеря данных: при использовании алгоритмов сжатия данных с потерями, некоторые информационные биты могут быть утеряны окончательно.

2. Баланс между сжатием и сохранением качества

При выборе алгоритма сжатия, необходимо найти оптимальный баланс между степенью сжатия и сохранением качества данных. Это особенно важно в случае работы с мультимедийными данными, где потери качества могут быть более заметными.

Реализация алгоритма компрессии Хаффмана на Python

Алгоритм Хаффмана основан на построении оптимального префиксного кода для сжатия данных. Префиксный код означает, что ни одно кодовое слово не является префиксом другого кодового слова. Это позволяет нам однозначно определить, какую последовательность бит представляет каждый символ данных.

Прежде чем начать, вам понадобится библиотека heapq, которая позволит нам создать минимальную кучу (min-heap) для реализации алгоритма Хаффмана. Установите ее, выполнив следующую команду:

pip install heapq

Перейдем к коду.

import heapq
from collections import defaultdict

class Node:
    def __init__(self, frequency, value):
        self.frequency = frequency
        self.value = value
        self.left = None
        self.right = None

    def __lt__(self, other):
        return self.frequency < other.frequency

def build_huffman_tree(data):
    frequencies = defaultdict(int)
    for char in data:
        frequencies[char] += 1

    heap = []
    for char, freq in frequencies.items():
        heapq.heappush(heap, Node(freq, char))

    while len(heap) > 1:
        node1 = heapq.heappop(heap)
        node2 = heapq.heappop(heap)
        merged = Node(node1.frequency + node2.frequency, None)
        merged.left = node1
        merged.right = node2
        heapq.heappush(heap, merged)

    return heap[0]

def build_code_table(root):
    code_table = {}

    def traverse(node, code):
        if node.value is not None:
            code_table[node.value] = code
        else:
            traverse(node.left, code + '0')
            traverse(node.right, code + '1')

    traverse(root, '')
    return code_table

def compress_data(data):
    root = build_huffman_tree(data)
    code_table = build_code_table(root)

    encoded_data = ''
    for char in data:
        encoded_data += code_table[char]

    return encoded_data

def decompress_data(encoded_data, root):
    current_node = root
    decoded_data = ''

    for bit in encoded_data:
        if bit == '0':
            current_node = current_node.left
        else:
            current_node = current_node.right

        if current_node.value is not None:
            decoded_data += current_node.value
            current_node = root

    return decoded_data

# Пример использования
data = "example data for compression"
encoded_data = compress_data(data)
print('Encoded data:', encoded_data)

decoded_data = decompress_data(encoded_data, build_huffman_tree(data))
print('Decoded data:', decoded_data)

Давайте пошагово проанализируем этот код.

1. Мы начинаем с определения класса Node, который представляет узел дерева Хаффмана. Узел содержит поле frequency для хранения частоты символа и поле value для хранения символа данных. Кроме того, у узла есть левый и правый потомки, представляемые полями left и right.

2. В функции build_huffman_tree мы сначала создаем словарь frequencies, где ключами являются символы данных, а значениями — их частоты. Затем мы создаем пустую кучу heap и помещаем каждый символ в виде экземпляра Node соответствующей частотой в эту кучу. Мы продолжаем объединять два узла с наименьшей частотой, пока не останется только один узел — корень дерева Хаффмана.

3. Функция build_code_table строит таблицу кодов для каждого символа, начиная от корневого узла дерева.

4. В функции compress_data мы используем созданную таблицу кодов для преобразования исходных данных в строку битов, представляющих сжатые данные.

5. Функция decompress_data выполняет обратный процесс, используя корень дерева и строку битов сжатых данных, чтобы восстановить исходные данные.

6. Для примера мы создаем строку data и сжимаем ее с помощью функции compress_data. Затем мы декомпрессируем сжатые данные, используя функцию decompress_data и выводим на экран.

Это простой пример использования алгоритма Хаффмана для сжатия данных с помощью Python. Вы можете дальше исследовать этот алгоритм, чтобы сделать его более эффективным или реализовать другие алгоритмы сжатия данных.

Заключение

В заключение, алгоритмы компрессии данных являются неотъемлемой частью современных информационных технологий, обеспечивая более эффективное использование ресурсов и повышая скорость передачи данных. Они представляют собой важный инструмент для оптимизации хранения и передачи данных, и их применение может быть весьма выгодным для различных областей, включая интернет-сервисы, мультимедийные приложения и информационные системы.

Хотите узнать про алгоритмы больше? Регистрируйтесь на бесплатный вебинар от моих коллег из OTUS, где вас познакомят с маленьким чудом — алгоритмом поиска подстроки в строке Кнута-Морриса-Пратта. Это маленький, но очень непростой для понимания алгоритм, поэтому, чтобы в нём разобраться вы сначала построите конечный автомат для поиска шаблона, а потом оптимизируете его: замените двумерную матрицу перехода префиксным Пи-вектором и узнаете, как решить эту задачу за линейное время.

Зарегистрироваться на вебинар

© Habrahabr.ru