Алгоритмы для веб-разработчиков простыми словами

Здравствуйте, друзья! Данным постом мы открываем цикл статей об алгоритмах и структурах данных.
В этой статье мы поговорим о том, зачем вообще их нужно знать веб-разработчикам, и затронем тему оценки сложности алгоритмов и Big O нотации.
Зачем мне алгоритмы? Я фронтендер!
Вы наверняка задумались: «А зачем мне нужно тратить своё время на изучение этих сложных алгоритмов, если я работаю с фронтендом? Как знание графов и бинарных деревьев поможет мне лучше отцентровать одну div-ку внутри другой div-ки?»
С одной стороны, знание алгоритмов и структур данных действительно напрямую не пригодится вам в практической работе. Но с другой стороны, существует одна весомая причина инвестировать немного своего времени в их изучение: знание алгоритмов и структур данных сделает вас лучше как разработчика.
Многие веб-разработчики на таких форумах, как Reddit и Stack Overflow, отмечали, что, освоив даже на базовом уровне эти фундаментальные основы программирования, чувствовали себя увереннее, профессиональнее и писали более чистый и структурированный код.
Также это помогло им прокачать главный скилл разработчика — умение логически думать и решать сложные технические задачи.
Кстати, именно по этой причине многие крупные IT-компании требуют от своих потенциальных сотрудников знания фундаментальных основ computer science, к которым как раз относятся алгоримты и структуры данных, и с пристрастием спрашивают их на собеседованиях (даже на позицию фронтенд-разработчика!).
Ведь они ищут лучших из лучших, и знание алгоритмов как раз делает вас лучше как разработчика. Тем более, лучше инвестировать свое свободное время в новые знания и навыки, чем в сериалы на Netflix.
И на этой прекрасной ноте давайте перейдем к основной теме статьи.
Что такое алгоритмы и структуры данных
Алгоритм — это совокупность последовательных операций, направленных на решение определенной задачи.
Структуры данных — это особый способ организации и хранения данных в компьютере, который обеспечивает эффективный доступ к этим данным и их изменение. Для оценки сложности и скорости работы алгоритма используют так называемую «О-нотацию» или «О-большое».
Эта запись имеет вид O(n), где n — это количество операций, которое предстоит выполнить алгоритму. Важное замечание: O(n) всегда описывает худший возможный случай выполнения алгоритма. Это дает нам гарантию, что наш алгоритм никогда не будет работать медленнее O(n).
Скорость работы алгоритмов измеряется не в секундах, а в темпе роста количества операций. Т.е. нас интересует, насколько быстро возрастает время выполнения алгоритма с увеличением размера входных данных.
Вот так выглядит время работы некоторых алгоритмов:
O(1) — константное время. Например, чтение данных из ячейки в массиве.
O(log n) — логарифмическое время. Например, бинарный поиск.
O(n) — линейное время. Например, поиск наименьшего или наибольшего элемента в неотсортированном массиве.
O(n * log n) — линейно-логарифмическое время. Например, быстрая сортировка.
O(n2) — квадратичное время. Например, сортировка пузырьком.
O(n!) — факториальное время. Например, решение задачи коммивояжера полным перебором.
Алгоритм линейного поиска
Давайте для начала рассмотрим такой простейший алгоритм, как линейный поиск элемента в массиве, и реализуем его на JavaScript.
Итак, есть массив чисел, и нам нужно найти в нем конкретное число.

Создадим функцию линейного поиска и назовем ее linearSearch. Эта функция будет принимать в себя два параметра: array (т.е. сам массив элементов, в котором ведется поиск) и item (элемент, который мы ищем в этом массиве).
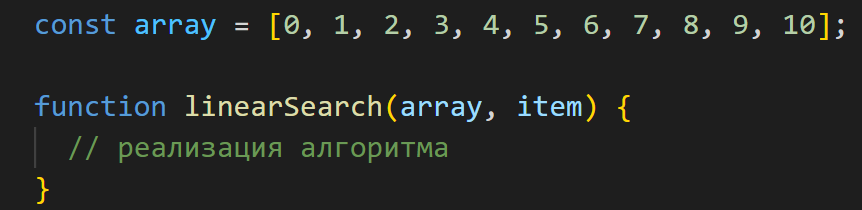
Линейный поиск происходит достаточно предсказуемо: мы используем цикл for, в котором пробегаемся по элементам массива и сравниваем каждый элемент с искомым.
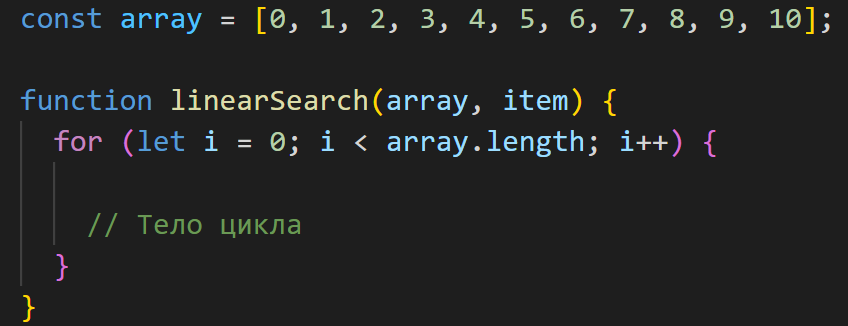
Далее инициализируем счётчик и установим его исходное значение, которое будет равно нулю, так как мы собираемся проверять массив с самого первого элемента.
let i = 0;
Наш цикл будет выполняться до тех пор, пока не пройдет по всем элементам массива. В качестве конечной точки мы используем значение array.length, которое возвращает количество элементов в массиве. Так как массив array начинается с нулевого индекса, то мы используем при сравнении знак »<».
i < array.length;
После каждой итерации цикла увеличиваем значение переменной i на единицу.
i++
Далее с помощью условной конструкции if будем проверять на истинность одно условие. Данная проверка будет выполняться при каждой итерации цикла, но код внутри нее сработает только один раз, после чего функция завершится.
Здесь мы сравниваем каждый элемент массива (array[i]) c искомым элементом (item) и, если эти элементы совпадают, то возвращаем i (индекс массива, по которому находится этот искомый элемент item).

Если же искомый элемент не был найден, то по завершении работы цикла мы возвращаем -1.

Дальше нам остается только вызвать функцию linearSearch, первым параметром передать в нее массив элементов, а вторым параметром — искомое число.
Затем, с помощью функции console.log, выводим результат в консоль.

Продублируем код для копирования:
const array = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
function linearSearch(array, item) {
for (let i = 0; i < array.length; i++) {
if (array[i] === item) {
return i;
}
}
return -1;
}
console.log(linearSearch(array, 5)); // Вызываем функцию и получаем 5.Как видите, алгоритм линейного поиска довольно прост в реализации. Сложность данного алгоритма: линейное время или O(n).
Давайте теперь рассмотрим более сложный и интересный алгоритм, который еще называют алгоритмом бинарного поиска.
Алгоритм бинарного поиска
Бинарный (или двоичный) поиск — это алгоритм, при котором массив данных будет последовательно делиться пополам до тех пор, пока не будет обнаружен искомый элемент.
Важное замечание: данный алгоритм будет работать только для отсортированного массива.
Бинарный поиск может быть реализован следующим образом:
0. Берём исходный массив отсортированных данных (например, по возрастанию).
1. Делим его на две части и находим середину.
2. Сравниваем элемент в середине с искомым элементом.
3. Если искомое число меньше этого центрального элемента — продолжаем искать элемент в левой части массива. Для этого мы делим левую часть массива на 2 части. Если искомый элемент больше центрального элемента, то мы отбрасываем левую часть массива и продолжаем поиск в правой.
И повторяем данную процедуру до тех пор, пока не найдем искомый элемент. Как только мы его нашли, то возвращаем индекс в массиве, по которому он находится. Если же данный элемент не будет найден, то возвращаем -1.
Давайте сначала взглянем на реализацию данного алгоритма, а потом разберем ее детально.
const arr = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
const binarySearch = (arr, value) => {
let start = 0;
let end = arr.length - 1;
while (start <= end) {
let middle = Math.floor((start + end) / 2);
if (value === arr[middle] ) return middle;
if (value < arr[middle]) {
end = middle - 1;
} else {
start = middle + 1;
}
}
return -1;
};
console.log(binarySearch(arr, 5)); // 5Итак, у нас есть массив чисел arr, отсортированный по возрастанию. Как вы помните, если заранее не отсортировать массив, то бинарный поиск не будет работать.

Создаем функцию binarySearch и передаем в нее два параметра: отсортированный массив arr и искомый элемент value.
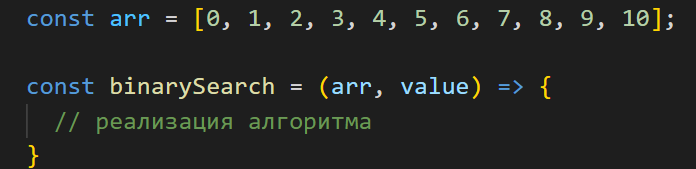
Затем определяем следующие переменные:
let start = 0;
Так как мы должны найти центральный элемент, то сначала необходимо определить начальный и конечный элементы.
Задаем таким образом начальный элемент и устанавливаем его значение равным нулю, так как наш массив начинается с нулевого индекса.
let end = arr.length - 1;
Затем определяем конечный элемент. Его позиция будет вычисляться по длине массива arr.length - 1.
Далее мы создадим цикл while, который будет работать до тех пор, пока начальная и конечная позиция массива не сравняются (start <= end).
let middle;
Внутри цикла мы будем высчитывать позицию центрального элемента в массиве и сохранять ее в переменную middle. Для этого мы складываем начальную позицию с конечной и делим результат на две части.
Результат обернем в функцию Math.floor(), так как в результате деления у нас может получиться дробное число. С помощью данной функции мы округляем полученное число до нижней границы.

Далее с помощью условной конструкции if создаем проверку: если центральный элемент в массиве по индексу middle равен искомому элементу, то мы возвращаем индекс найденного элемента, сохраненный в переменной middle. И на этом наша функция завершает свою работу.
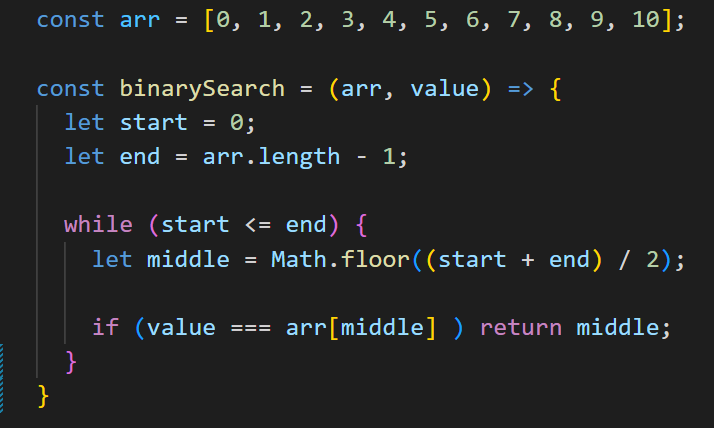
Если на данной итерации цикла мы не нашли искомый элемент, то необходимо выполнить еще одну проверку с помощью условной конструкции if. Если искомый элемент меньше, чем элемент, находящийся в середине, то это значит, что нам нужно продолжить поиск в левой части массива, а правую можно отбросить.
Для этого нам нужно изменить значение переменной end. В итоге мы получим end = middle + 1. А в блоке else мы прописываем такое же условие, только для случая, если искомый элемент будет больше, чем элемент, находящийся в середине. Тогда мы отбрасываем левую часть массива и продолжаем поиск в правой.

После завершения цикла while возвращаем -1 на случай, если искомое число не будет найдено в массиве. Далее вызываем функцию binarySearch и передаем в нее два параметра: массив элементов и искомое число.
И выводим результат в консоль.

Что касается оценки сложности приведенных алгоритмов: бинарный поиск эффективнее линейного, поскольку массив данных на каждом шаге разделяется надвое и одна половина сразу отбрасывается.
Последовательная сложность бинарного поиска в худшем и среднем случаях равна O(log n), в лучшем — O(1) (если обнаруживаем искомый элемент на первой итерации). Для сравнения: вычислительная сложность линейного поиска, как вы помните, равна O(n).
На этом мы закончили первую статью из нашего цикла статей по алгоритмам. Спасибо за внимание.
