Алгоритмы быстрого возведения в степень08.12.2023 21:00

Автор статьи — Виктория Ляликова

В настоящее время мы уже так привыкли пользоваться готовыми решениями, что при написании высокоуровневого кода, даже не задумываемся над тем, а как вообще реализованы те или иные инструменты. И уж конечно, при возведении чисел в степень, мы никогда не задумываемся о том, а как вообще все это реализовано. И какие существуют алгоритмы для этого?

Возведение числа в степень является одной из основных операций в математике. Что вообще такое возведение в степень? Как нам известно еще со школы — это многократное умножение числа на себя. Но проблема кроется в том, что при возведении больших чисел в очень большие степени вычисления могут занять много времени.

Многие из алгоритмов быстрого возведения в степень основаны на том, что для возведения в степень n числа x не обязательно перемножать x на само себя n раз, а можно перемножать уже вычисленные степени. Также некоторые алгоритмы используют тот факт, что операции возведения в квадрат быстрее операции умножения за счет того, что при возведении в квадрат цифры в сомножителе повторяются. Однако некоторые алгоритмы не всегда оптимальны.

Зачем нам нужны алгоритмы быстрого возведения в степень? Например в криптографии быстрое возведение в степень используется для шифрования и расшифровки данных. Криптографические алгоритмы оперируют числами длиной в тысячи бит. В машинном обучении быстрое возведение в степень используется при обучении и тестировании различных моделей: статистических, нейросетевых, обработке изображений и др. Программы для защиты паролей и других конфиденциальных данных тоже не обходятся без возведения в степень. И этот список можно продолжать дальше. Можно переходить к рассмотрению алгоритмов.

Рекурсивное возведение в степень

Можно заметить, что для любого четного числа x и n выполнимо очевидное тождество

x^n=(x^{n/2})^2=x^{n/2}\cdot{x^{n/2}}

То есть всего за одну операцию умножения можно свести задачу к вдвое меньшей степени.

Таким образом, показатель степени в четном представляется в виде

x^{2^m}=(((x^2)^2)^2…)^2.

Если n нечетна, тогда можно перейти к степени (n-1), которая уже будет четной.

x^n=x^{n-1}\cdot{x}

Таким образом, у нас есть реккурентная формула: от степени n мы переходим, если она четна к n/2, а иначе — к n-1.

И тогда потребуется всего лишь m умножений, точнее возведений в квадрат.

Распространим это полезное наблюдение на общий случай, воспользовавшись очевидным равенством

\color{blue}{x}^\color{green}n=\begin{cases}\color{blue}{x}(\color{blue}{x}^2)^{(\color{green}{n}-1)/2} &\text {если $\color{green}{n}$ нечетное} \ (\color{blue}x^2)^{\color{green}{n}/2}, &\text{если $\color{green}{n}$ четное} \ 1, &\text {если $\color{green}{n}=0$ } \end {cases}

Если показатель степени n<0, тогда

\color{blue}{x}^{\color{green}{-n}}=\Big (\frac{1}{\color{blue}{x}}\Big)^\color{green}{n}=\frac{1}{\color{blue}{x}^\color{green}{n}}

Всего будет не более 2logn переходов, прежде чем мы придем к n=0. Таким образом, мы получили алгоритм, работающий за O (log n) умножений.

Количество умножений, которое следует выполнить для возведения в степень в соответствии с описанной рекурсивной процедурой, вычисляется по формуле \mu_n=\xi_n+2\varepsilon_n-2, где \xi_n и \varepsilon_n — количество соответственно нулей и единиц в двоичной записи числа n.Эта величина растет крайне медленно с ростом n.

Например, если нам придется возводить число в 10000000000-ю степень, то мы обошлись бы всего 43 умножениями. Посмотрим на рекурсивный алгоитм

def my_power(val,p):
    if p<0:
        return my_power(1/val, -p)
    if p==0:
        return 1
    if p%2 == 0:
        return my_power(val*val, p/2)
    else:
        return val*power(val*val,(p-1)/2)

При каждом рекурсивном вызове в этом алгоритме удаляются младшие цифры двоичного представления степени n. Получается, что количество рекурсивных вызовов равно количеству битов двоичного представления n. Таким образом этот алгоритм вычисляет количество квадратов равное количеству рекурсивных вызовов и требует меньшего количество умножений, которое равно количеству 1 в двоичном представлении n.

Но есть ограничение для этого алгоритма связанное с требуемым объем вспомогательной памяти, который примерно пропорционален количеству рекурсивных вызовов — или, возможно больше, если объем на итерацию увеличивается.

Бинарный алгоритм возведения в степень

Один из самых популярных и эффективных способов возведения в степень. Данный алгоритм основан на двоичной записи показателя степени и свойстве возведения в квадрат, что позволяет ускорить вычисления при работе с большими числами. За счет использования двоичной записи показателя степени, бинарное возведение позволяет провести минимально возможное количество операций умножения, вследствие чего время вычисления степени существенно сокращается. Также данный алгоритм гарантирует правильность результата при любых значениях входных данных.

Суть бинарного метода заключается в том, что степень, в которую необходимо возвести число представляется в двоичном виде. И далее начинается проход по битам этого двоичного числа. Такой проход повторяется до тех пор, пока все биты не будут обработаны.

Существует бинарные алгоритмы, использующие схему «слева направо» и схему «справа налево». Для всех этих схем количество операций возведения в квадрат одинаково и равко k, где k — длина показателя степени в n битах, k\sim{ln (n)}. Количество же операций умножения равно количеству ненулевых элементов в двоичной записи числа n. В среднем требуется \frac{1}{2}\cdot{ln (n)} операций умножения. Например, для возведения числа в сотую степень этим алгоритмом потребуется всего лишь 8 операций умножения и возведений в квадрат. Для сравнения, при стандартном способе возведения в степень требуется n-1 операций умножения, то есть количесвто операций может быть оценено как O (n).

Схема «слева направо»

Название фактически говорит само за себя, в данной схеме биты показателя степени просматриваются слева направо, то есть от старшего к младшему.

Представим показатель степень n в двоичной системе n = (m_km_{k-1}…m_1m_0)2

Тогда

n=\color{green}{m_k}\cdot2^\color{green}{^k}+\color{blue}{m{k-1}}\cdot2^\color{blue}{{k-1}}+…\color{purple}{m_1}\cdot2\color{purple}{^1}+\color{red}{m_0}

где m_i = {0,1}

Тогда число x в степени n можно записать так

x_n=x^{((…((m_k\cdot2+m_{k-1})\cdot2+m_{k-2})\cdot2+…)\cdot2+m_1)\cdot2+m_0}

x_n={((…(((x^{\color{green}{m_k}})^2x^{\color{blue}{m_{k-1}}})^2…)^2x^\color{purple}{m_1})x^\color{red}{m_0}}

И алгоритм возведения в степень при использовании данной схемы можно описать следующим образом

Представить показатель степени n в двоичном коде.
Зафиксировать индекс i и изменять его от k-1 до 0.
Если m_i=1, то текущий результат возводить в квадрат и затем умножать на х.
Если m_i=0, то текущий результат просто возводить в квадрат.

Или можно представить алгоритм так

\begin{cases}s_1=x \ s_{i+1} = s_i^2{\cdot}x^{m_k-i} \ i=1,2,…, k \end {cases}

Применим алгоритм, вычислив 21_{11}, x=21, n=11

11_{10}=\color{green}{1}\color{blue}{0}\color{purple}{1}\color{red}{1}2

\color{green}{m_3} = 1, \color{blue}{m_2} = 0, \color{purple}{m_1} = 1, \color{red}{m_0} =1

21{11}=(((1\cdot21^\color{green}{m_3})^2\cdot21^\color{blue}{m2})^2\cdot21^\color{purple}{m_1})^2\cdot21^\color{red}{m_0}=

0=(((1\cdot21^\color{green}{1})^2\cdot21^\color{blue}{0})^2\cdot21^\color{purple}1)^221^\color{red}{1}=

=(((1\cdot21)^2\cdot1)^2\cdot21)^2\cdot21=

=(((21)^2)^2\cdot21)^2\cdot21=

=(((441)^2\cdot21)^2\cdot21=

=(194 481\cdot21)^2\cdot21=

=4084101^2\cdot21=

=350277500542221

Реализация в Python

def my_power(val, p):
    res, v, c = 1, val, p
    if c &1:
        res = v
    c>>=1    
    while c>0:
        v = v * v
    	   if c&1:
            res = v*res
    	   c = c>>1
    return res

или

def my_power(val, p):
    res, v, c = 1, val, p
    bin_k = list(map(int,bin(p)[2:]))
    for i in range(len(bin_k)):
        res = res * res
        if bin_k[i] == 1:
            res = res*v
    return res

Схема «справа налево»

Здесь, в отличие от схемы «слева направо» биты показателя степени просматриваются от младшего к старшему.

Алгоритм возведения в степень при использовании данной схемы можно описать следующим образом

Представить показатель степени n в двоичном коде.
Ввести вспомогательную переменную y равной числу x.
Зафиксировать индекс i и изменять его от 0 до k-1.
Если m_i =1, то текущий результат умножается на y, а само число y возводится в квадрат.
Если m_i=0, то требуется только возвести y в квадрат.

Данная схема содержит столько же умножений и возведений в квадрат, сколько и схема слева направо.

В, общем виде схему можно записать

x^n=x^\color{red}{m_0}\cdot (x^2)^\color{purple}{m_1{}}\cdot ({x^{2^2}})^{\color{blue}m_2}\cdot…\cdot (x^{2^k})^\color{green}{m_k}

или

x^n=\prod\limits_{i=0}^k (a^{2^i})^{m_i}

Воспользовавшись формулой схемы возведения в степень справа налево посчитаем 21_{11}

В данном случае m_\color{red}{m_0} = 1, \color{purple}{m_1} =1, \color{blue}{m_2} = 0, \color{green}{m_3} = 1

21^{11}=21^{\color{red}{m_0}}\cdot (21^2){^{\color{purple}{m_1}}}\cdot (21^{2^2}){^{\color{blue}{m_2}}}\cdot (21^{2^{2^2}})^\color{green}{m_3}=

=21^\color{red}{1}\cdot (21^2){^\color{purple}{1}}\cdot (21^{2^2}){^\color{blue}{0}}\cdot (21^{2^{2^2}})^\color{green}{1}=

=21^{11}=21\cdot21^2\cdot21^{2^{2^2}}=21\cdot441\cdot37822859361=

=9261\cdot37822859361=350277500542221

Реализация в Python

def fast_pow(val, p):
    s, v,c =1,val,p
    while (c!=0):
        if (c %2==1):
            s = s* v
        c = c>>1  
        v = v*v
    return s

Лестница Монтгомери

Данный алгоритм часто используется в криптографии, так как обеспечивет защиту от актак по побочным каналам и позволяет сохранить показатель степени в секретности. Основная идея лестницы в том, что умножения происходят независимо от конкретного значения бита, то есть от того, что именно в показателе степени 0 или 1. Это дает то, что постоянно происходят разные вычисления и извне сложно понять что именно вообще происходит.

Для возведения числа х в степень n алгоритм можно представить следующим образом.

Ввести вспомогательные переменные x_1 и x_2. x_1=x, x_2=x^2
Зафиксировать индекс i и изменять его от k-1 до 0.
Если m_i=0, тогда x_2=x_1\cdot{x_2}, x_1=x^2_1.
Если m_i=1, тогда x_1=x_1\cdotx_2, x_2=x^2_2.
В переменной x_1 будет храниться результат возведения числа x в степень n.

Алгоритм выполняет фиксированную последовательность операций (от до log n): умножение и возведение в квадрат имеют место для каждого бита в степени независимо от конкретного значения бита.

Рассмотрим пример возведения числа 21 в степень 11. Представим показатель степени в двоичной системе.

11_{10}=\color{green}{1}\color{blue}{0}\color{purple}{1}\color{red}{1}_2

x_1=1, x_2=21
\color{green}{m_3}=1

x_1=21\cdot1=21, x_2 = 21^2=441

\color{blue}{m_2} = 0

x_2 = 21\cdot441=9261

x_1=21^2=441

\color{purple}{m_1} = 1

x_1 = 441cdot9261=4084101

x_2 = 9261^2 = 85766121

\color{red}{m_0} = 1

x_1=4084101cdot85766121 = 350277500542221

x_2=85766121^2

Результат 21^{11} = 350277500542221

def powers(val,p):
    x1 = 1
    x2 = val
    bin_k = list(map(int,bin(p)[2:]))
        for i in range(len(bin_k)):
            if bin_k[i]==0:
        	    x2 = x1*x2
        	    x1 = x1*x1
            else:
        	    x1 = x1*x2
        	    x2 = x2*x2   
    return x1

Метод множителей

Данный метод основан на представлении показателя степени в виде произведения множителей. Для этого метода необходимо раскладывать показатели степени в произведение простых множителей и возводить число в каждую из них. Таким образом, можно значительно ускорить процесс возведения в степень. Данный метод широко используется в задачах, связанных с криптографией и шифрованием данных, а также в задачах вычислительной математики. Известно, что любое натуральное число можно разложить на произведение простых чисел и такое разложение называется факторизацией. Например

11 = 11^1

100=2\cdot2\cdot5\cdot5=2^2\cdot5^2

126=2\cdot3\cdot3\cdot7 = 2^1\cdot3^2\cdot7^1

Разложение числа на простые множители в общем виде можно представить так

n=p^{a_1}_1\cdot{p^{a_2}_2}\cdot…\cdot{p^{a_k}_k}.

Для того, чтобы разложить число на множители воспользуемся методом перебора делетелей. Будем перебирать простой делитель от 2 до корня из n и если n делится на этот делитель, то будем на него делить. И возможно нам понадобится делить несколько раз. Так мы сможем набрать простые делители и остановимся в тот момент, когда n станет либо 1, либо простым.

def factorize(n):
    factors = []
    i =2
    while i*i<=n: # перебираем простой делитель
        while n%i==0: # пока n на него делится
        	n//=i # делим на этот делитель
        	factors.append(i)
    	i +=1
# возможно n стало простым числом
# и его тоже надо добавить в разложение    
        if n>1:
            factors.append(n)
    return factors

После того, как получили разложение, можно возводить число в степень

def power_fact(n,p):
    lists = factorize(p)
    result = n
    for el in lists:
        result = result**el
    return result

Бином Ньютона

Скорее бином Ньютона не совсем относится к алгоритмам бстрого возведения в степень, но считаю, что в рамках статьи его можно рассмотреть. Бином Ньютона является формулой разложения произвольной натуральной степени суммы двух чисел в многочлен. То есть он поможет посчитать сумму двух чисел, возведенных в любую степень. Магия Бинома заключается в простоте и скорости.

Из уроков математики мы все помним такую формулу

(a+b)^2=a^2+2ab+b^2.

И это тоже бином Ньютона, а точнее его частный случай.

В общем виде формула принимает вид

(a+b)^n=C^0_n\cdot{a^n}+C^1_n\cdot{a^{n-1}}\cdot{b}+…+C^{n-1}n\cdot{a}\cdot{b^{n-1}}+C^n_n\cdot{b^n}

или

(a+b)^n=\sum{k=0}^{n}C_n^k\cdot{a^{n-k}}\cdot{b^k}

числа С^n_m — биномиальные коэффициенты

C^m_n=\frac{n!}{m!(n-m)!} — число сочетаний из n по m.

C^0_n=1, C^n_n=1

Исходя из формулы для расчета бинома нам много раз надо будет посчитать факториал, то есть произведение всех чисел целых чисел от единицы до заданного числа. А факториалы в силу рекурсивности едят очень много оперативной памяти. Может так случиться, что при подсчете факториалов закончится оперативная память. И для этого на помощь приходит треугольник Паскаля.

Треугольник Паскаля — это специальный треугольник, в котором каждое число равно сумме двух чисел расположенных над ним. На вершине и по ребрам треугольника расположены единицы. Строки треугольника симметричны относительно вертикальной оси. Такой треугольник можно продолжать бесконечно.

Например, биномиальные коэффициенты для n=4

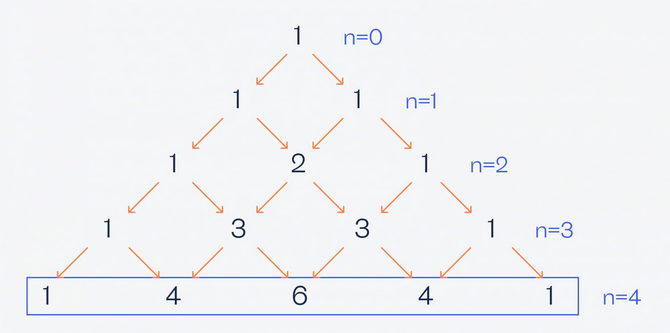
Тогда получим следующий бином

(x+y)^\color{blue}{4}=\color{red}{1}x^\color{blue}{4}+\color{green}{4}x^\color{blue}{3}y\color{blue}{^1}+\color{purple}{6}x^\color{blue}{2}y^\color{blue}{2}+\color{green}{4}x^\color{blue}{1}y^\color{blue}{3}+\color{red}{1}y^\color{blue}{4}.

Из полученного многочлена можно заметить, что сумма степеней всегда равна n, а биномиальные коэффициенты симметричны.

Таким образом с помощью такого треугольника можно обойтись без всех этих факториалов, а просто быстро находить нужные коэффициенты, подставлять их в формулу бинома и получать ответ.

Используя бином Ньютона можно возводить очень большие числа в заданную степень раскладывая их на сумму двух чисел поменьше, а слагаемые считать через бином. Также бином Ньютона применяется в алгоритмах сжатия данных, криптографии и задачах связанных с комбинаторикой и вероятностями. Биномиальные коэффициенты часто применяются в матрицах и операциях с векторам, а на матрицах построены почти все нейронные сети.

Найдем коэффициенты в разложении Бинома

def my_binom(n):
    res=[1]
    for i in range(n):
        res=[1]+[res[i]+res[i+1] for i in range(len(res)-1)]+[1]
    return res

И посчитаем разложение бинома

def binoms(a,b,n):
    res = 0
    k = 0
    koef = my_binom(n)
    while k<= n:
        res = res+koef[k]*a**(n-k)*b**k
        k = k+1
    return res

За рамками статьи остались некоторые методы, которые являются еще более оптимальными, чем алгоритмы бинарного возведения в степень. К ним можно отнести алгоритмы с названием «метод окна», «метод скользящего окна». Смысл этих методов заключается в том, за один проход можно просмотреть не один, а несколько бит показателей степени, а также во время выполнения процесса можно изменять ширину окна, то есть количество просматриваемых битов.

Как еще можно ускорить вычисления. Если нужно многократно возводить одно и тоже число в разные степени, то можно использовать таблицу предвычисленных значений и обращаться к ней по индексу. Также можно использовать кэширование результатов вычислений, чтобы не повторять уже сделанные вычисления. Например, в Pyton для этого можно использовать декоратор @lru_cache из модуля functools. Если необходимо возводить в степень комплексные числа, тогда можно использовать функцию cmath.exp (), которая возводит его в заданную степень. Также важно учитывать особенности языка программирования и выбирать подходящие структуры.

Материал подготовлен для будущих студентов онлайн-курса OTUS «Математика для программистов». 13 декабря в рамках курса пройдет открытый урок «Разработка своего языка программирования с помощью ANTLR», на который приглашаем всех желающих. На занятии определим синтаксис и семантику Тьюринг-полного языка программирования. Записаться можно здесь.