Алгоритм триангуляции Делоне методом заметающей прямой24.03.2019 17:20

Доброго времени суток!

В этой статье я подробно опишу алгоритм, который у меня получился в результате использования идеи «заметающей прямой» для построения триангуляции Делоне на плоскости. В нем есть несколько идей, которые я нигде не встречал, когда читал статьи про триангуляцию.
Возможно, кто-то тоже найдет их необычными. Я постараюсь сделать все в лучших традициях и включить в рассказ следующие вещи: описание используемых структур данных, описание шагов алгоритма, доказательство корректности, временные оценки, а также сравнение с итеративным алгоритмом, использующим kD-дерево.

Определения и постановка задачи

Триангуляция

Говорят, что на множестве точек на плоскости задана триангуляция, если некоторые пары точек соединены ребром, любая конечная грань в получившемся графе образует треугольник, ребра не пересекаются, и граф максимален по количеству ребер.

Триангуляция Делоне

Триангуляцией Делоне называется такая триангуляция, в которой для любого треугольника верно, что внутри описанной около него окружности не находится точек из исходного множества.

Замечание: для заданного множества точек, в котором никакие 4 точки не находятся на одной окружности, существует ровно одна триангуляция Делоне.

Условие Делоне

Пусть на множестве точек задана триангуляция. Будем говорить, что некоторое подмножество точек удовлетворяет условию Делоне, если триангуляция, ограниченная на это подмножество, является триангуляцией Делоне для него.

Критерий для триангуляции Делоне

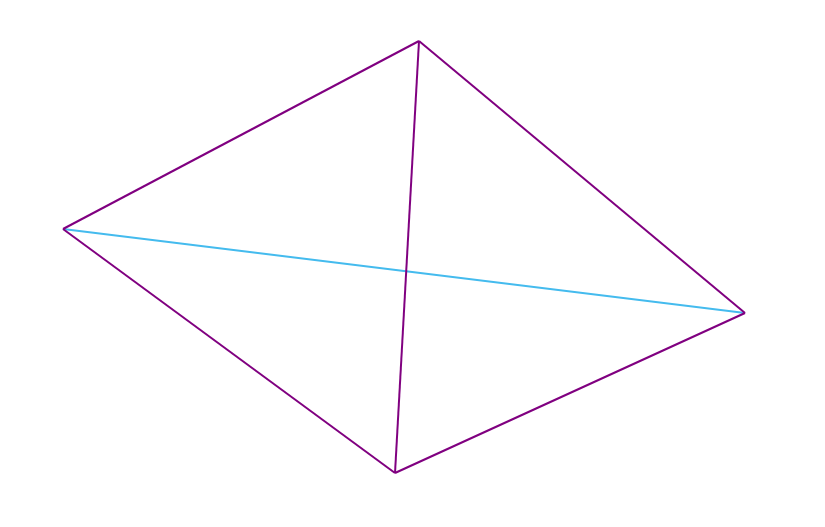
Выполнение условия Делоне для всех точек, образующих четырехугольник в триангуляции, эквивалентно тому, что данная триангуляция является триангуляцией Делоне.

Замечание: для невыпуклых четырехугольников условие Делоне всегда выполнено, а для выпуклых четырехугольников (вершины которого не лежат на одной окружности) существует ровно 2 возможные триангуляции (одна из которых является триангуляцией Делоне).

Задача заключается в том, чтобы для заданного множества точек построить триангуляцию Делоне.

Описание алгоритма

Видимые точки и видимые ребра

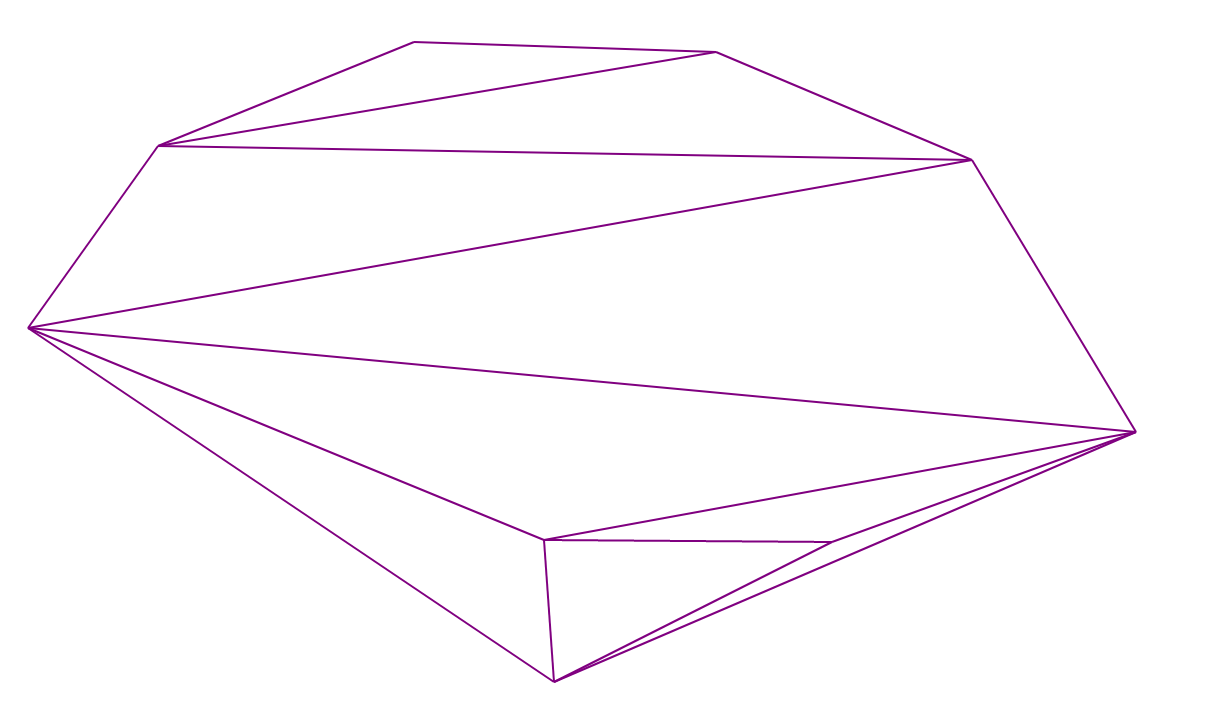
Пусть задана минимальная выпуклая оболочка (далее МВО) конечного множества точек (ребра, соединяющие некоторые из точек так, чтобы они образовывали многоугольник, содержащий все точки множества) и точка A, лежащая вне оболочки. Тогда точка плоскости называется видимой для точки А, если отрезок, соединяющий ее с точкой А, не пересекает МВО.

Ребро МВО называется видимым для точки А, если его концы видимы для А.

На следующей картинке красным помечены ребра, видимые для красной точки:

Замечание: контур триангуляции Делоне является МВО для точек, на которых построена.

Замечание 2: в алгоритме видимые для добавляемой точки А ребра образуют цепочку, то есть несколько подряд идущих ребер МВО

Хранение триангуляции в памяти

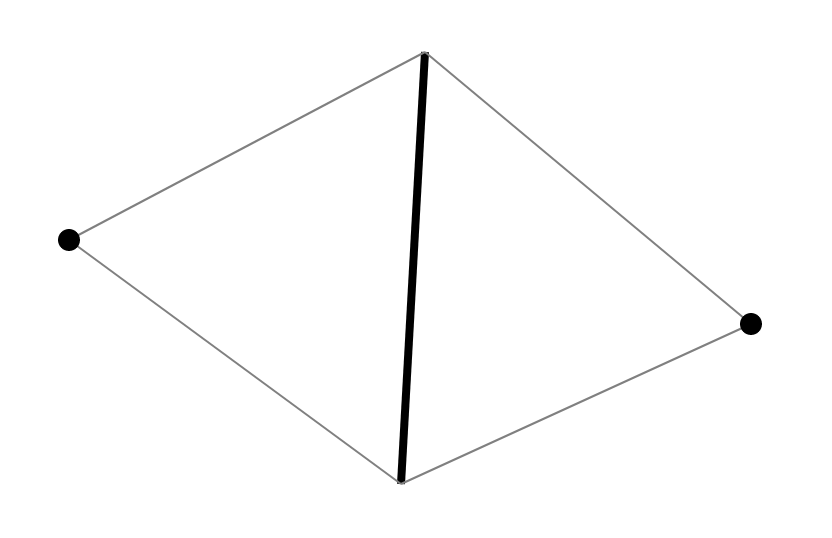
Есть некоторые стандартные способы, неплохо описанные в книге Скворцова [1]. Ввиду специфики алгоритма, я предложу свой вариант. Так как хочется проверять 4-угольники на условие Делоне, то рассмотрим их строение. Каждый 4-угольник в триангуляции представляет из себя 2 треугольника, имеющих общее ребро. У каждого ребра есть ровно 2 треугольника, прилегающих к нему. Таким образом, каждый четырехугольник в триангуляции порождается ребром и двумя вершинами, находящимися напротив ребра в прилегающих треугольниках.
Так как по ребру и двум вершинам восстанавливаются два треугольника и их смежность, то по всем таким структурам мы сможем восстановить триангуляцию. Соответственно предлагается хранить ребро с двумя вершинами в множестве и выполнять поиск по ребру (упорядоченной паре вершин).

Алгоритм

Идея заметающей прямой заключается в том, что все точки сортируются по одному направлению, а затем по очереди обрабатываются.

Отсортируем все точки вдоль некоторой прямой (для простоты по координате ).
Построим треугольник на первых 3 точках.
Далее для каждой следующей точки будем выполнять шаги, сохраняющие инвариант, что имеется триангуляция Делоне для уже добавленных точек и, соответственно, МВО для них.
Добавим треугольники, образованные видимыми ребрами и самой точкой (то есть добавим ребра из рассматриваемой точки во все концы видимых ребер).
Проверим на условие Делоне все четырехугольники, порожденные видимыми ребрами. Если где-то условие не выполнилось, то перестроим триангуляцию в четырехугольнике (напоминаю, что их всего две) и рекурсивно запустим проверку для четырехугольников, порожденных ребрами текущего четырехугольника (ибо только в них после изменения условие Делоне могло нарушиться).

Замечание: в шаге (4) при рекурсивном запуске можно не проверять четырехугольники, порожденные ребрами, исходящими из рассматриваемой на данной итерации точки (их всегда два из четырех). Чаще всего они будут невыпуклыми, для выпуклых доказательство чисто геометрическое, оставлю его на читателя. Далее будем считать, что выполняется только 2 рекурсивных запуска на каждое перестроение.

Проверка условия Делоне

Способы проверки четырехугольников на условие Делоне можно найти в той же книжке [1]. Подмечу лишь, что при выборе метода с тригонометрическими функциями оттуда при неаккуратной реализации могут получаться отрицательные значения синусов, есть смысл брать их по модулю.

Поиск видимых ребер

Осталось понять, как эффективно находить видимые ребра. Заметим, что предыдущая добавленная точка S находится в МВО на текущей итерации, так как имеет наибольшую координату $x$ , а также видима для текущей точки. Тогда, замечая, что концы видимых ребер образуют непрерывную цепочку видимых точек, мы можем идти от точки S в обе стороны по МВО и собирать ребра, пока они видимы (видимость ребра проверяется с помощью векторного произведения). Таким образом удобно хранить МВО как двусвязный список, на каждой итерации удаляя видимые ребра и добавляя 2 новых из рассматриваемой точки.

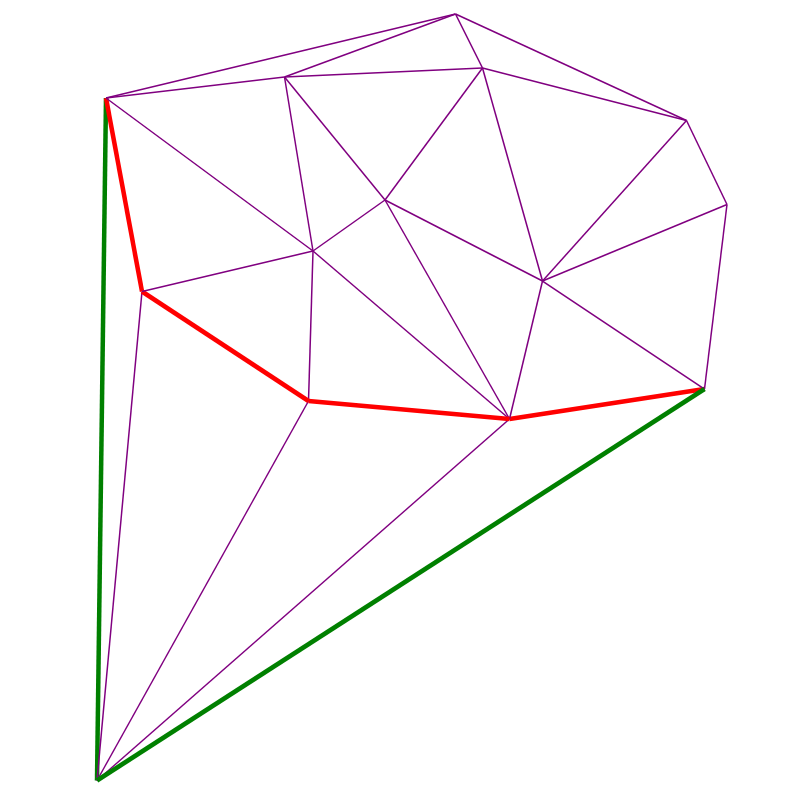
Визуализация работы алгоритма

Две красные точки — добавляемая и предыдущая. Красные ребра в каждый момент составляют стек рекурсии из шага (4):

Корректность алгоритма

Чтобы доказать корректность алгоритма, достаточно доказать сохранение инварианта в шагах (3) и (4).

Шаг (3)

После шага (3), очевидно, получится некоторая триангуляция текущего множества точек.

Шаг (4)

В процессе выполнения шага (4) все четырехугольники, не удовлетворяющие условию Делоне, находятся в стеке рекурсии (следует из описания), а значит, по окончании шага (4) все четырехугольники удовлетворяют условию Делоне, то есть действительно построена триангуляция Делоне. Тогда осталось доказать, что процесс в шаге (4) когда-нибудь закончится. Это следует из того, что все ребра, добавленные при перестроении, исходят из текущей рассматриваемой вершины (то есть на шаге $k$ их не больше, чем $k-1$ ) и из того, что после добавления этих ребер мы не будем рассматривать четырехугольники, порожденные ими (см. предыдущее замечание), а значит, добавим не более одного раза.

Временная сложность

В среднем на равномерном, нормальном распределениях алгоритм работает довольно неплохо (результаты приведены ниже в табличке). Есть предположение, что время его работы составляет $O(NlogN)$ . В худшем случае имеет место оценка $O(N^2)$ .

Давайте разберем время работы по частям и поймем, какая из них оказывает самое большое влияние на итоговое время:

Сортировка по направлению

Для сортировки будем использовать оценку $O(NlogN)$ .

Поиск видимых ребер

Для начала покажем, что время, суммарно затраченное на поиск видимых ребер, есть $O(N)$ . Заметим, что на каждой итерации мы находим все видимые ребра и еще 2 (первые не видимые) за линейное время. В шаге (3) мы добавляем в МВО новые 2 ребра. Таким образом, всего в меняющейся на протяжении алгоритма МВО побывает не более $2N$ ребер, значит, и различных видимых ребер будет не более $2N$ . Еще мы найдем $2N$ ребер, не являющихся видимыми. Таким образом, в общей сложности найдется не более $4N$ ребер, что соответствует времени $O(N)$ .

Построение новых треугольников

Суммарное время на построение треугольников из шага (3) с уже найденными видимыми ребрами, очевидно, $O(N)$ .

Перестроение триангуляции

Осталось разобраться с шагом (4). Сначала заметим, что проверка условия Делоне и перестроение в случае его не выполнения являются довольно дорогими действиями (хоть и работают за $O(1)$ ). Только на проверку условия Делоне может уйти около 28 арифметических операций. Посмотрим на среднее количество перестроений в течение этого шага. Практические результаты на некоторых распределениях приведены ниже. По ним очень хочется сказать, что среднее количество перестроений растет с логарифмической скоростью, однако оставим это как лишь предположение.

Здесь еще хочется подметить, что от направления, вдоль которого производится сортировка, может сильно варьироваться среднее число перестроений на точку. Так на миллионе равномерно распределенных на длинном низком прямоугольнике с отношением сторон 100000:1 это число варьируется от 1.2 до 24 (эти значения достигаются при сортировке данных по горизонтали и вертикали соответственно). Поэтому я вижу смысл выбирать направление сортировки произвольным образом (в данном примере при произвольном выборе в среднем получалось около 2 перестроений) или выбрать его вручную, если данные заранее известны.

Таким образом, основное время работы программы обычно уходит на шаг (4). Если же он выполняется быстро, то есть смысл задуматься над ускорением сортировки.

Худший случай

В худшем случае на $k$ -ой итерации происходит $k-1$ рекурсивный вызов в шаге (4), то есть, суммируя по всем i, получаем асимптотику в худшем случае $O(N^2)$ . Следующая картинка иллюстрирует красивый пример, на котором программа может работать долго (1100 перестроений в среднем при добавлении новой точки при входных данных в 10000 точек).

Сравнение с итеративным алгоритмом построения триангуляции Делоне с использованием kD-дерева

Описание итеративного алгоритма

Коротко опишу вышеуказанный алгоритм. При поступлении очередной точки мы с помощью kD-дерева (советую почитать про него где-нибудь, если вы не знаете) находим довольно близкий к ней уже построенный треугольник. Затем обходом в глубину ищем треугольник, в который попадает сама точка. Достраиваем ребра в вершины найденного треугольника и фактически выполняем шаг (4) из нашего алгоритма для новых четырехугольников. Так как точка может быть вне триангуляции, то для упрощения предлагается накрыть все точки большим треугольником (построить его заранее), это решит проблему.

Сходство алгоритмов

На самом деле, если точки добавляются в отсортированном по направлению порядке, то наш алгоритм фактически работает также, как итеративный, разве что количество перестроений меньше. Следующая анимация это отлично демонстрирует. На ней точки добавлялись справа налево, и все они накрыты большим треугольником, который впоследствии удаляется.

Различия алгоритмов

В итеративном алгоритме локализация точки (поиск нужного треугольника) происходит в среднем за $O(logN)$ , на вышеуказанных распределениях в среднем происходит 3 перестроения (как показано в [1]) при условии произвольного порядка подачи точек. Таким образом заметающая прямая выигрывает время у итеративного алгоритма в локализации, но проигрывает его в перестроениях (которые, напомню, довольно тяжелые). Ко всему прочему итеративный алгоритм работает в режиме онлайн, что также является его отличительной особенностью.

Заключение

Здесь я просто покажу некоторые интересные триангуляции, получившиеся в результате работы алгоритма.

Красивый узор

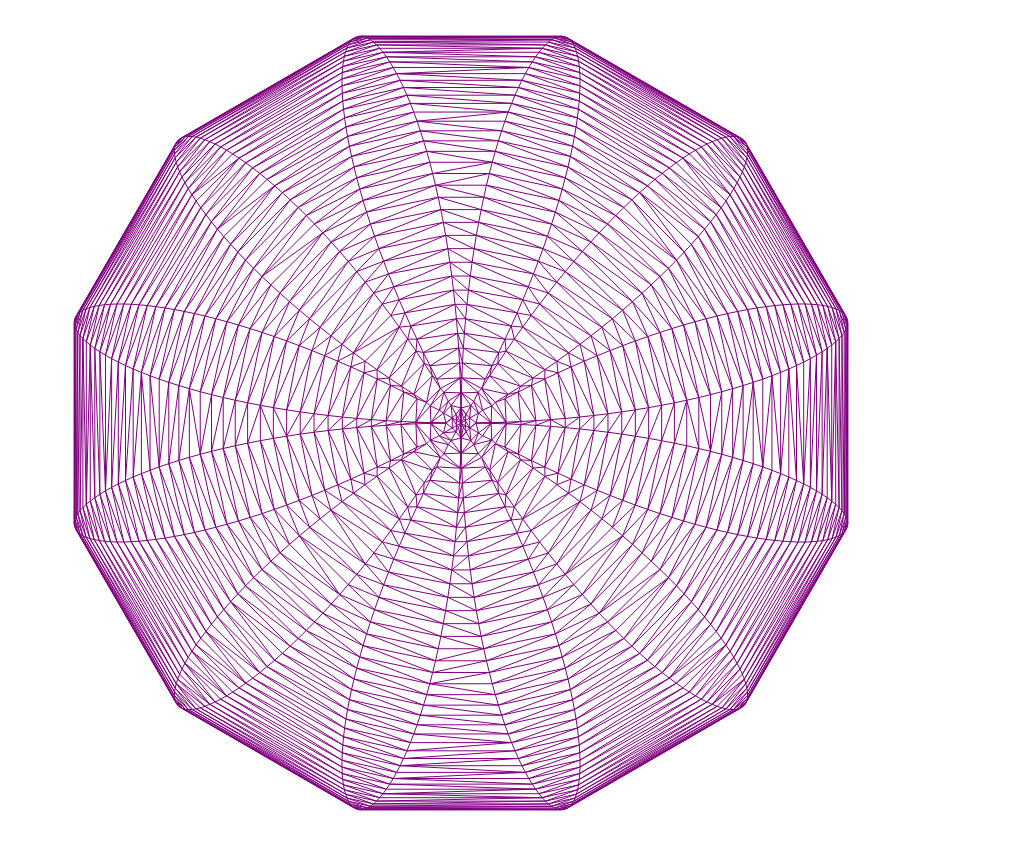
Нормальное распределение, 1000 точек

Равномерное распределение, 1000 точек

Триангуляция, построенная на местоположениях всех городов России

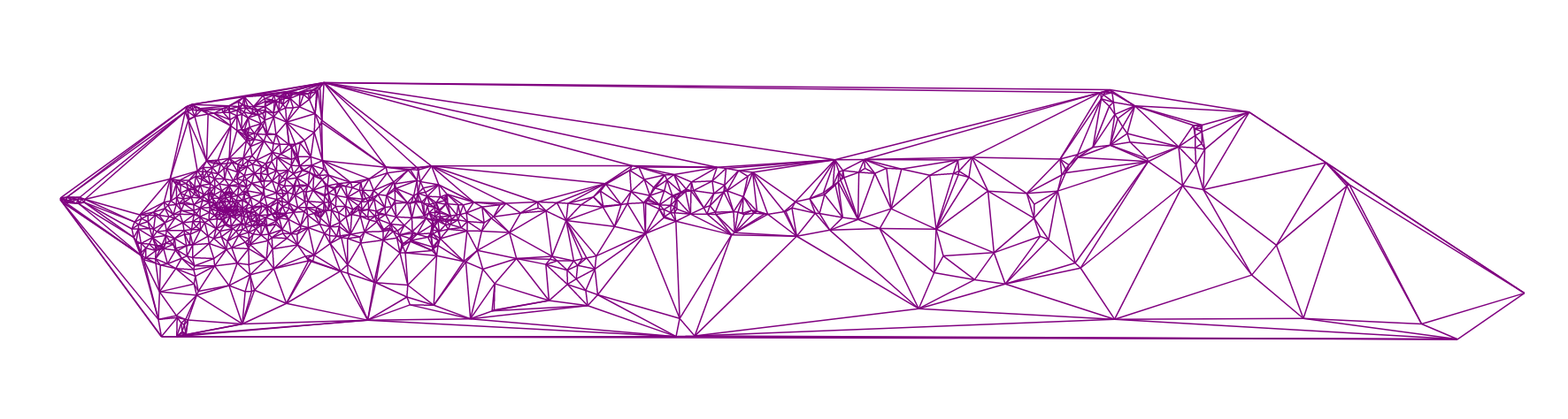
Спасибо за внимание!

Литература

[1] Скворцов А.В. Триангуляция Делоне и её применение. — Томск: Изд-во Том. ун-та, 2002. — 128 с. ISBN 5–7511–1501–5