Алгоритм Quickhull для нахождения выпуклой оболочки
Как гласит определение, выпуклая оболочка некоторого множества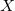 
— это наименьшее выпуклое множество 
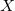, содержащее в себе это множество . Выпуклой оболочкой конечного множества попарно различных точек является многогранник.Для реализации одномерного случая алгоритма Quickhull годится функция std: minmax_element. В сети можно найти множество реализаций алгоритма Quickhull для плоского случая. Однако, для случая произвольной размерности сходу находится лишь одна тяжёловесная реализация с сайта qhull.org. В скобках рядом с терминами я буду давать перевод на английский (в стиле Туґбо, уж извините). Это может быть полезно для тех, кто ещё не знаком с терминами и будет читать англоязычные тексты по ссылкам, либо решит разобраться с текстами исходного кода.Упомянутая выше «каноническая» реализация написана на C (есть C++ биндинги), используется давно и широко (в составе пакетов GNU Octave и MATLAB) и, следовательно, хорошо проверена. Но если вы решите изолировать код, относящийся только лишь к одному алгоритму Quickhull, то столкнётесь со сложностями. Для простейших применений хотелось бы иметь возможность обходится чем-то более компактным. Немного постаравшись, я написал свою реализацию (https://bitbucket.org/tomilov/quickhull/): это единственный класс, без зависимостей. Всего порядка 750 строк.Геометрические понятия.Начиная работать с многомерными сущностями, понимаешь, что справедливы какие-то аналогии с привычными двухмерными и трёхмерными объектами. Необходимо несколько упорядочить знания: ввести некоторые новые термины и прояснить отношения между ними.Для программиста геометрические объекты — это прежде всего структуры данных. Для начала я дам геометрические определения (не очень строгие). Дальше по тексту будут приведены описания соответственных структур данных, удобных для того, чтобы хранить данные и оперировать с ними достаточно эффективно.Обозначим размерность пространства как 
.Симплекс (англ. simplex) задаётся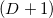 
аффинно независимой (англ. affinely independent) точкой. Об аффинной независимости поясню далее. Эти точки называются вершинами (англ. ед. vertex, мн. vertices).
Многогранник (син. политоп, многогранник, полиэдр, англ. polytope, polyhedron) определяется как минимум 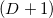аффинно независимой точкой (вершиной); симплекс (англ. simplicial polytope) — простейший случай -мерного тела, многогранники с меньшим числом вершин обязательно будут иметь нулевой -мерный объём. Параллелотоп (англ. parallelotope) — обобщение плоского параллелограмма и объёмного параллелепипеда. Для симплекса можно построить 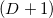соответственных параллелотопов (все они будут иметь одинаковый объём, равный 
объёмам симплекса), взяв в качестве образующих (векторов) параллелотопа вектора, выходящие из одной фиксированной вершины в остальные вершины.
Понятие выпуклого многогранника (англ. convex polytope, convex polyhedron) я здесь приводить не буду, сгодится ваше интуитивное представление о нём. Симплекс, как частный случай многогранника, всегда является выпуклым.
Понятие плоскости я также приводить не буду. Только замечу, что она имеет на единицу меньшую размерность, чем пространство, в которое вложена.
Симплициальная грань (англ. simplicial facet) определяется аффинно независимыми точками (вершинами). Далее речь будет идти только о симплициальных объектах (кроме выпуклого многогранника), так что определение «симплициальный» я буду опускать. Многие утверждения в дальнейшем будут справедливы только для невырожденных (все точки попарно различны) случаев симплициальных геометрических объектов.
Ребро (англ. ridge) определяется как пересечение двух граней и имеет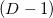 
вершину. Две грани могут иметь только одно общее ребро. Одна грань, таким образом, может иметь соседей через рёбра.
Пик (англ. peak) определяется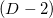 
точками. Здесь интуитивная аналогия с трёхмерным пространством может поплыть, так как понятие пика и вершины не совпадают, но такими объектами мы не будем оперировать. Грань может иметь любое количество соседних граней через пик, отсюда можно сделать вывод, что хранить граф смежности граней через пики накладно и по памяти и по затратам на поддержку актуальности структур данных при каких-либо преобразованиях.
Грань многогранника, её границы, границы её границ и т.д. на английском именуются face. Дам ссылку на хороший ресурс, где логически обосновывается, что в -мерном пространстве видимыми или наблюдаемыми объектами могут являться только лишь 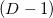-мерные объекты, то есть границы (англ. boundaries) -мерных объектов. Английский термин facet — это именно наблюдаемая грань. Прямая (англ. straight line) — это всегда одномерная сущность. Точку (вершину) можно в этой градации считать нуль-мерной.Имея дело с некоторым набором из 
точек, мы можем перейти к рассмотрению соответственного набора из 
векторов, вычтя одну из точек из всех других. Таким образом мы как бы назначим эту точку началом координат (англ. origin). Если все точки лежали в одной плоскости, то плоскость смещается таким образом, что начинает проходить через начало координат. Аффинная независимость точек выполняется, когда выполняется линейная независимость -го соответственного вектора. Определение линейной независимости векторов вам скорей всего уже знакомо. Таким образом в -мерном пространстве нельзя выбрать больше 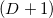точки так, чтобы все они были аффинно независимы. Поясню это: в трёхмерном пространстве треугольник (грань трёхмерного симплекса — тетраэдра) задан тремя точками (не лежащими на одной прямой, конечно); через эти три точки проходит единственная плоскость; любая точка этой плоскости, добавленная ко множеству из трёх вершин треугольника превратит можнество трёх аффинно независимых точек в множество 4 аффинно зависимых. Аналогия справедлива для других размерностей.Кроме всего прочего необходимо ввести понятие гиперобъёма (англ. hypervolume).Гиперобъём. Любой рассмотреный объект из ряда симплекс, грань, ребро, пик и т.д. ограничены в соответственном подпространстве. «Количество места», которое такой объект занимает, можно измерить/определить/задать. Для одномерной прямой мера называется длиной; для двумерной плоскости, мера называется площадью; для трёхмерного тела — объём. Понятие можно обобщить, назвав D-мерным объёмом или D-гиперобъёмом. Для симплекса, образованного попарно различными точками 
(порядок перечисления точек важен), гиперобъём вычислить можно так: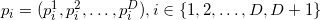 
Здесь мы выписали координаты векторов в строки. Аналогичные формулы и рассуждения можно привести и для векторов-столбцов (т.е. если мы транспонируем все матрицы, то на результат и выводы это не повлияет).Делитель детерминанта в формуле выше — это количество симплексов (все они имеют одинаковый объём), на который можно разбить параллелотоп 
, построенный на векторах 
. Соответственно сам детерминант — это гиперобъём параллелотопа. Интересующимся основаниями, лежащими в основе этого утверждения, рекомендую прочитать про определитель матрицы Грама и о его геометрической интерпретации.Следует отметить, что данная мера для «объёмных» объектов будет иметь ненулевое значение, а также может быть как положительной, так и отрицательной величиной. Понять смысл знака нетрудно из следующих соображений: при обмене местами двух точек симплекса мы получаем смену знака детерминанта; порядок точек — это «лево- и право- ориентированность» симплекса. На плоскости это несложно себе представить: если стороны треугольника 
перечислены против часовой стрелки 
, то определитель положителен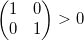 
, иначе 
— отрицателен 
. Для тетраэдра знак будет зависеть от того, в каком порядке (по часовой стрелке или против) первые 3 точки будут перечисляться при взгляде на них из последней. Таким образом, в дальнейшем, при задании геометрических объектов, мы должны принять, что порядок перечисления точек должен быть фиксированным.Множитель перед детерминантом мы можем опустить, так как в алгоритме будет использоваться лишь информация о знаке величины ориентированного гиперобъёма.Детерминант равен нулю, если хотя бы две строки линейно зависимы (помним, что точки попарно различны, то есть ни одна строка не нулевая). Несложно проверить соответствие приведённых выше рассуждений об аффинно зависимых точках и линейно зависимых векторах, соответствующих им.На абсолютное значение детерминанта не будет влиять то, какую именно точку вычитаем при переходе к векторам, — только на знак. Следует вычитать всегда последнюю точку из первых, иначе для одинаково ориентированных аналогичных объектов, используемых в дальнейшем, знак меры будет разным в чётных и нечётных размерностях.Что же делать с мерой для объектов, вложенных в пространство слишком большой размерности, например, с гранями? Если мы сконструируем матрицу так же, как это показано выше, то она будет прямоугольная. Детерминант от такой матрицы взять не получится. Оказывается формулу можно обобщить (это обобщение связано с формулой Бине-Коши), используя всё ту же матрицу составленную из векторов-строк:
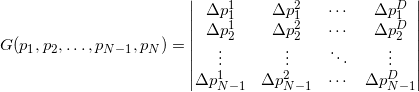
Для аффинно независимых попарно различных точек матрица под детерминантом всегда получается квадратной положительно определённой, а сам детерминант такой матрицы — число всегда положительное. Для аффинно зависимых точек матрица получится сингулярной (т.е. её определитель равен нулю). Ясно, что мера всегда неотрицательная и информации об ориентации мы не имеем.С одной стороны детерминант произведения квадратных матриц равен произведению детерминантов, с другой — детерминант транспонированной квадратной матрицы совпадает с детерминантом исходной, таким образом последняя формула сводится к формуле для 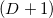точки, за исключением корня из квадрата, т.е. модуля, который мы можем опустить, с целью получить дополнительную информацию об относительной ориентации точек в пространстве.
Алгоритм.
Сам алгоритм Quickhull для случая произвольной размерности был предложен в труде Barber, C. Bradford; Dobkin, David P.; Huhdanpaa, Hannu (1 December 1996). «The quickhull algorithm for convex hulls». ACM Transactions on Mathematical Software 22 (4): 469–483. «Каноническая» реализация на C от авторов располагается на уже упомянутом сайте http://qhull.org/, репозиторий с C++ интерфейсом https://gitorious.org/qhull/qhull. Процитирую алгоритм из первоисточника:
create a simplex of d + 1 points
for each facet F
for each unassigned point p
if p is above F
assign p to F`s outside set
for each facet F with a non-empty outside set
select the furthest point p of F`s outside set
initialize the visible set V to F
for all unvisited neighbours N of facets in V
if p is above N
add N to V
the set of horizon ridges H is the boundary of V
for each ridge R in H
create a new facet from R and P
link the new facet to its neighbours
for each new facet F'
for each unassigned point q in an outside set of a facet in V
if q is above F'
assign q to F'`s outside set
delete the facets in V
Выпуклая оболочка представляет собой список граней.Стартовый симплекс.
Как видно, мы должны начать с некоторого стартового симплекса. Для этого можно выбрать любые 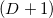аффинно независимые точки, но лучше использовать какую-нибудь дешёвую эвристику. Основное требование на этом шаге — чтобы наш симплекс по возможности не получился «узким» (англ. narrow). Это важно в случае, если используется арифметика с плавающей точкой (англ. floating-point arithmetic). В оригинальной реализации используются точки с максимальными и минимальными значениями координат (очевидно они же войдут во множество вершин выпуклой оболочки). Начав со стартового симплекса, на каждом последующем шаге мы будем получать всё больший и больший многогранник, неизменным свойством которого всегда будет его выпуклость. Я буду называть его временный многогранник.Эвристика поиска вершин для стартового симплекса.
Моя эвристика основана на последовательном выборе точек таким образом, чтобы каждая следующая находилась от всех предыдущих как можно дальше. «Дальше» — в некотором определённом смысле, который проясню далее.Ведётся два списка точек: исходный список 
(изначально в нём находятся все точки со входа алгоритма) и список точек симплекса 
(изначально — пустой). В соответствие множествам и можно поставить множества векторов 
и 
. Для этого мы мысленно на каждом шагу данного алгоритма выбираем любую точку 
из множества (д.б. не пустое), запомним её, затем проведём из неё вектора во все остальные точки из (получив при этом , которое будет содержать меньше на один элемент, чем ) и во все точки из (получив ). Вначале берём первую (или любую другую) точку из и перемещаем её в . Далее ищем вектор из с самым большим модулем и перемещаем соответственную точку из в . Первую же точку из перемещаем обратно в (она была выбрана без какого-либо критерия). На каждом из следующих шагов ищем точку 
из , которая максимально далека от аффинного пространства с базисом и перемещаем её из в . Для этого ищем соответствующий точке вектор 
из , модуль проекции которого на ортогональное дополнение 
векторного подпространства 
максимален. Здесь — линейная оболочка , то есть — векторное пространство, т.к. вектора в получаются линейно независимыми (по построению), то — базис этого векторного пространства.Формула расстояния от до : 
Так как вектор непосредственно раскладывается в сумму проекций на любое подпространство и на ортогональное дополнение этого подпространства, то: 
Имея ортонормированный базис 
векторного подпространства , мы можем вычислить модуль проекции на это подпространство: 
Координаты векторов 
мы можем получить, произведя QR-разложение прямоугольной матрицы (например, методом Хаусхолдера), составленной из (координат) столбцов-векторов из множества . В результате мы получим ортогональную (прямоугольную) матрицу Q (
) и верхнетреугольную R (не используется). Столбцы Q — это координаты векторов , образующих ортонормированный базис векторного пространства .После завершения алгоритма в находится 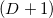точка.
Далее мы должны распределить оставшиеся точки в так называемые списки внешних точек (англ. outside sets) граней — это такие списки точек, которые ведутся для каждой грани и в которые попадают ещё не рассмотренные (далее — неназначенные, англ. unassigned) точки, находящиеся относительно плоскости грани по другую сторону, нежели внутренность симплекса (или временного многогранника в дальнейшем). Здесь мы пользуемся тем свойством выпуклого многогранника (и симплекса в частности), что весь он лежит целиком только в одном из двух полупространств, получаемых при разбиении всего пространства плоскостью каждой грани. Из этого свойства следует тот факт, что если точка не попала ни в один из списков внешних точек граней выпуклой оболочки, то она достоверно находится внутри неё. В дальнейшем в алгоритме понадобится информация о том, какая из точек, содержащихся в списке внешних точек и наиболее удалена от плоскости грани, поэтому, добавляя точки в список внешних точек, необходимо сохранять информацию о том, которая из них самая дальняя. Любая точка попадает только в один список внешних точек. На асимптотическую сложность не влияет то как именно распределяются точки по спискам.На данном этапе мне необходимо сделать отступление и рассказать о том, как задать грань, как вычислять расстояние до неё, как определить ориентацию точки относительно грани.Грань. Ориентированное расстояние от плоскости грани до точки.
Для задания грани нам необходимо иметь точек — вершин грани. По приведённым выше соображениям хранить мы эти точки будем упорядоченным образом. Причём упорядоченность нам нужна не абсолютно строгая. Например, совершив два обмена в любых двух не обязательно различных парах попарно различных точек, мы получим точно так же ориентированную грань в том смысле, что в любых операциях в дальнейшем (а это обычно будет взятие детерминантов от матриц, сформированных из констант и координат вершин) такие парные перестановки не влияют на результат. Двум возможным ориентациям соответствует два возможных направления нормали к плоскости (грани).Только лишь единожды — в самом начале — нам понадобится вычислить значение гиперобъёма стартового симплекса чтобы по знаку определить его ориентацию. Все дальнейшие операции касательно граней будут заключаться только лишь в вычислении ориентированного расстояния (англ. directed distance) до точки. Здесь мы можем вспомнить школьную формулу, допускающую обобщение на случай произвольной размерности, а именно: «площадь треугольника равна половине произведения основания, на высоту» или «объём пирамиды равен одной третьей от произведения площади основания на высоту». Меру тела и грани мы высилять умеем, следовательно мы можем выразить высоту (одномерную длину): 
В алгоритме нам понадобится вычислять ориентированное расстояние от фиксированной плоскости (грани) до точек, которых может быть много. В этом случае мы можем заметить, что в знаменателе стоит положительная константа. От положения точки («над» или «под») зависит лишь гиперобъём в числителе. — тоже константа. Таким образом мы можем рассматривать только относительные величины гиперобъёмов симплексов (а точнее, соответственных параллелотопов) построенных из грани и точки. Если определитель считать не самым медленным способом (по определению за 
) и не самым быстрым (
), а способом через LUP-разложение (англ. LUP-decomposition), то можно добиться сложности 
и приличной численной устойчивости (англ. numerical stability). Не берусь оценивать как сложность вычисления детерминанта влияет на конечную сложность всего алгоритма, но экспериментируя я заключил, что в худшем случае (например, случай точек расположенных на сфере (англ. cospherical points)) даже при малых размерностях пространства (
) вычисление детерминантов для оценки расстояния слишком вычислительно затратно.Другой подход — это использование нормированного уравнения плоскости (англ. hyperplane equation). Это уравнение первой степени, которое связывает координаты точки 
плоскости, координаты нормированного вектора нормали 
(
— ненормированная нормаль) к плоскости (англ. normalized normal vector) и её смещения 
от начала координат (англ. offset): 
Координаты нормали : 
Величина — смещение плоскости от начала координат: 
Невязка , получаемая при подстановке произвольной точки в нормированное уравнения плоскости, — это как раз ориентированное расстояние от плоскости до точки.
Если точка лежит по ту же сторону от плоскости, куда направлена нормаль, то величина 
будет положительной, иначе — отрицательной.Отличие матрицы под детерминантом в выражениях для 
и 
только лишь в замене 
-ой координаты (столбца) на единицы.Таким образом для плоскости грани необходимо вычислить и хранить 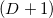число: координат нормированной нормали и смещение от начала координат. Вычисление расстояния сводится к вызову функции std: inner_product, в которую передаются итераторы начала и конца массива координат нормированной нормали, начало массива координат точки, а последним параметром — значение 
. Так как везде далее в алгоритме используются лишь относительные значения расстояний, то, вообще говоря, можно и не нормировать, но это довольно дешёвая операция, а правильное значение расстояния может понадобиться и при работе с выпуклой оболочкой после действий алгоритма.
Теперь описывать плоскость грани мы умеем, но осталась одна неясность: как же выбрать порядок перечисления точек в списках вершин граней стартового симплекса? Авторы не хранят список вершин упорядоченным. Они поступают иначе. Задав уравнение плоскости для произвольного, но фиксированного порядка вершин, они выясняют ориентацию какой-либо внутренней точки (англ. inner point) относительно этой плоскости. То есть вычисляют ориентированное расстояние. В случае, если расстояние отрицательное они меняют знак у координат нормали к гиперплоскости и у её смещения от начала координат. Либо задают значение флага, сигнализирующее о том, что грань перевёрнута (англ. flipped). Внутренней точкой для выпуклого многогранника будет среднее арифметическое хотя бы 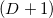его вершин (т.н. центр масс, если взять все вершины).Переориентация граней стартового симплекса.
В моей реализации на любом этапе алгоритма грани временного многогранника (а равно и стартового симплекса и финальной выпуклой оболочки) ориентированы вовне. Для стартового симплекса я вычисляю его гиперобъём, причём строки матрицы я формирую из координат векторов, проведённых из последней вершины (
) в первые (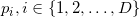
). Если таким образом вычесленный гиперобъём отрицателен, то точка находится «под» гранью с вершинами 
и порядок точек правильный, иначе мы должны обменять любые две точки местами (например первую и последнюю). Так как необходимо произвести обмен двух обязательно различных точек, то такой приём не сработает для случая 
(ограничение на 
как раз отсюда). В этом случае нужно менять знак координат нормали и смещения.Первая грань и следующая грань с вершинами имеют общее ребро 
. Если мысленно взглянуть на симплекс снаружи и обойти сначала первую грань в порядке возрастания номеров точек, а затем так же вторую, то общее ребро при этом будет пройдено в противоположных направлениях. Следовательно решение о том, обменивать ли местами две вершины должно быть противоположным аналогичному решению для первой грани. И так далее (решение о смене знака/порядка каждый раз меняется).Следует отметить, что в массиве точек, с целью сформировать наборы из вершин для граней симплекса, мы движемся из конца в начало, исключая очередную точку и начиная именно с последней точки. Это жёстко связано с тем, что мы решили вычитать именно последнюю точку из первых при вычислении гиперобъёма симплекса.
Для каждой грани кроме задания списка вершин, списка внешних точек необходимо задать список соседних (англ. adjacency list) граней. Для каждой грани он будет содержать ровно элементов. Так как стартовый симплекс содержит 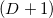грань, то очевидно, что для любой его грани в список соседних граней попадут все остальные грани ( штук).Главный цикл.
Теперь есть временный многоугольник с которым можно работать в главном цикле. В главном цикле этот временный многоугольник достраивается, «захватывая» всё больше и больше пространства, а вместе с ним и точки исходного множества, пока не настанет такой момент, когда вовне многогранника не останется ни одной точки. Далее опишу этот процесс более подробно. А именно, то, как он устроен в моей реализации.Главный цикл — это цикл по граням. На каждой итерации среди граней с непустыми списками внешних точек выбирается самая лучшая грань 
(англ. best facet); лучшая в том смысле, что самая дальняя точка из списка внешних точек находится дальше от грани, чем у других граней. Цикл завершается, когда граней с непустыми списками внешних точек не осталось.В теле главного цикла выбранная грань удаляется как заведомо не являющаяся гранью выпуклой оболочки. Но предварительно она «разбирается на составляющие». Из списка внешних точек извлекается самая дальняя точка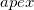 
(англ. furthest point) — она наверняка является вершиной выпуклой оболочки. Остальные точки перемещаются в отдельный временный список неназначенных точек 
. Далее по спискам соседних граней, начиная со списка грани , обходится граф смежности граней временного многогранника и каждая грань добавляется в список уже посещённых (англ. visited) граней и тестируется на видимость (англ. visibility) из точки 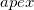. Если грань невидимая из точки 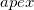, то её соседние грани далее не обходятся, иначе обходятся. Если у очередной видимой грани среди соседних граней есть невидимые из точки 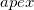, то она попадает в список граничных видимых граней (англ. before-the-horizon как противоположность over-the-horizon — «загоризонтный»). Но если все соседние грани являются видимыми, то такая грань добавляется в список граней на удаление. После обхода графа смежности граней список граничных видимых граней и список граней на удаление в сумме содержат все видимые из точки 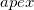грани. Теперь удаляются все грани из списка на удаление. Причём каждая удаляемая грань не удаляется из списков соседних граней у своих соседей. Так делать безопасно, потому что даже в случае если соседняя грань является граничной видимой гранью, из списка её соседних граней в дальнейшем используется только информация о соседстве с невидимыми из точки гранями. Следом за списокм граней на удаление просматривается список граничных видимых граней. Каждая граничная видимая грань «разбирается» (далее понадобится её список соседних граней и список вершин) и удаляется. Для каждой граничной видимой грани создаются новые грани (от одной до штук), которые добавляются в список новых граней. При этом просматривается список её соседних граней и для каждой грани из этого списка, являющейся невидимой, ищется общее ребро с данной граничной видимой гранью. В список ве
