Алгоритм поиска смещения объекта на изображении
В прошлой статье я описал простой алгоритм распознавания движущихся объектов на динамической картинке. А сейчас я опишу несколько другую ситуацию. Допустим, у нас уже есть координаты объекта и нам надо определить, в какую сторону он сместился. Под координатами я подразумеваю координаты какой-либо условной точки на объекте, для простоты принимая допущения, что объект не меняет ориентацию в пространстве. То, что сам объект сместился, можно определить путем вычитания определенной области кадра из области другого кадра. В прошлой статье я как раз это и делал, только для целого кадра.
Может возникнуть соблазн решить эту задачу «в лоб» перебирая всю картинку. Однако, такая операция может быть слишком затратная по времени. Напрашивается какой-то другой алгоритм.
Итак, небольшой эксперимент, те же самые картинки, я предполагаю, что автомобиль двигался по прямой. Беру область размером 25 на 25 пикселей, смещаю его вдоль предполагаемой траектории движения автомобиля и подсчитываю суммарное отклонение яркости пикселей, вот программный код:
private void tsmiFindShift_Click(object sender, EventArgs e)
{
ImageMatrix matrix1 = create_matrix("D:\\3\\1.png");
ImageMatrix matrix2 = create_matrix("D:\\3\\2.png");
Bitmap picture = new Bitmap(matrix1.picture);
using (var wrapper = new ImageWrapper(picture, true))
{
int x1 = 110;
int x2 = x1+25;
int y1 = 140;
int y2 = y1+25;
int dx = 0;
int dy = 0;
StringBuilder sb = new StringBuilder();
for (dx = -100; dx < 200; dx++)
{
Int64 res = 0;
for (int i = x1; i < x2; i++)
{
for (int j = y1; j < y2; j++)
{
int light1 = matrix1.matrix[i, j];
int light2 = matrix2.matrix[i + dx, j + dy];
int light = Math.Abs(light2 - light1);
res = res + light;
}
}
sb.AppendFormat("{0}; {1};\n", res, dx);
}
System.IO.File.WriteAllText("D:\\3\\1.txt", sb.ToString());
pbImage.Image = picture;
}
Смотрим полученный график:
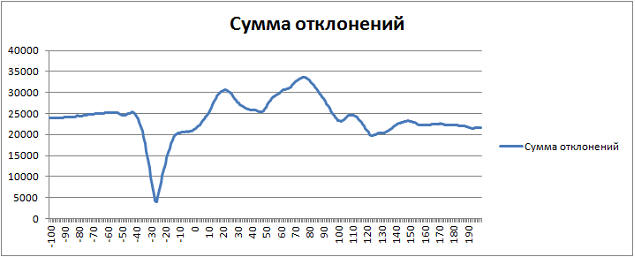
Что у нас получается? В некоторой точке эта сумма отклонений минимальная, но не нулевая. Почему не нулевая? Возможно, направление автомобиля было не совсем по прямой, также это могли быть различные шумы (например, капли дождя, дрожание руки и так далее). Чтобы проверить эту гипотезу, я все-таки провел эксперимент с поиском «в лоб», путем перебирания координат на большой области картинки. Оказалось, мое предположение было верно, автомобиль действительно двигался по прямой, так как наименьшее значение целевой функции оказалось именно при нулевом смещение по оси y, то есть, только горизонтально перемещение. Остается все списать на шумы. Хотя, еще не мешало бы посмотреть маску вычитания кадров в найденной точке:

В области вычитания видны края фар, видимо, просто какие-то блики.
Возникает вопрос: а можно ли применить для поиска нового положения объекта что-то вроде спуска по градиенту или поиск минимума целевой функции? Если внимательно посмотреть на график, то мы видим, что у функции довольно много локальных экстремумов, и пока непонятно, как сделать так, чтобы алгоритм локальный экстремум не спутал с главным.
Возникает вот такая идея: а что если воспользоваться бинарным поиском? Берем сначала функцию по оси x, затем по y, находим квадрант, где функция минимальная, делаим его на четыре таких же квадранта и так пока не найдем искомую точку. Это гораздо быстрее, чем обходить все точки области поиска.
Для эксперимента выбрана другая картинка: эллипс, смещающиеся одновременно и по горизонтали, и по диагонали:
Строим график целевой функции по оси x:
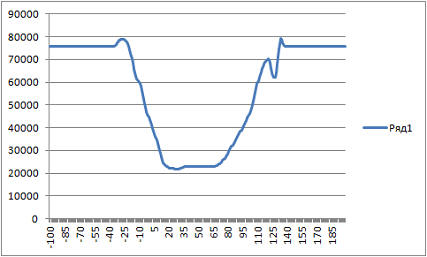
Экстремум функции при dx=24
И по оси y:
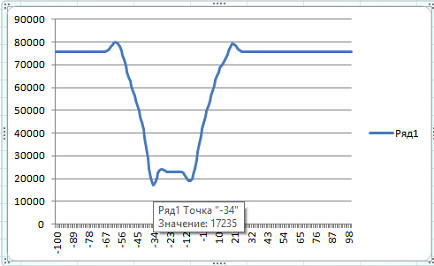
Экстремум в точке -34.
Как видим. по оси dy экстремум найден правильно, а по x — у нас оказалось, что объект смещен совсем в другой квадрант, экстремум в области dx>0, хотя на самом деле смещения было в сторону уменьшения x. Значит, нам нужен какой-то другой алгоритм.
Можно попробовать провести перпендикулярную прямую через точку экстремума и искать экстремум по ней. А потом через точку экстремуму на этой же прямой провести перпендикулярную линию. Таким образом, у нас прямая, на которой мы ищем экстремум, будет то параллельная оси Ox, то Oy. Итак, пробуем, нашли экстремум на Ox, ищем на оси, параллельной Oy при dx=24:

Экстремум при dy=-1. Проводим прямую через точку dx=24, dy=-1, параллельную уже оси Ox. получаем вот такой результат:

Теперь у нас экстремум уже в точке dx=18. Уже чуть ближе к истине. Вопрос только в чем: будет ли найден экстремум таким образом и насколько это будет эффективней, чем «тупым перебором»?
Итак, сначала тупой перебор. Алгоритм нашел экстремум в точке dx=-12, dy=-23 за 15556 итераций:
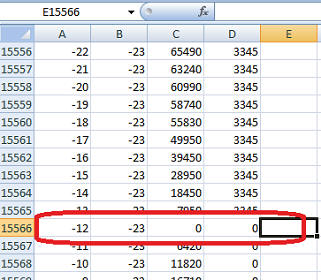
Всего итераций в данном примере возможно 40401. Время выполнения на моем ноутбуке примерно 0.7 секунд. Для обработки потокового видео такая скорость, разумеется, неприемлемая.
Теперь попробуем реализовать приведенную выше идею с постепенным приближением:
private ResStruct search(ImageMatrix matrix1, ImageMatrix matrix2, int x1, int y1, int x2, int y2, StringBuilder sb, int x_beg, int y_beg, int x_end, int y_end)
{
Int64 min_res = 999999999999999999;
ResStruct result = new ResStruct();
int min_dx = 999999999;
int min_dy = 999999999;
for (int dy = y_beg; dy <= y_end; dy++)
{
for (int dx = x_beg; dx <= x_end; dx++)
{
Int64 res = 0;
for (int i = x1; i < x2; i++)
{
for (int j = y1; j < y2; j++)
{
int light1 = matrix1.matrix[i, j];
int light2 = matrix2.matrix[i + dx, j + dy];
int light = Math.Abs(light2 - light1);
res = res + light;
}
}
if (res < min_res)
{
min_res = res;
min_dx=dx;
min_dy=dy;
}
//sb.AppendFormat("{0}; {1}; {2}; {3};\n", dx, dy, res, min_res);
}
}
result.dx = min_dx;
result.dy = min_dy;
result.res = min_res;
return result;
}
private void tsmiFastFindShift_Click(object sender, EventArgs e)
{
ImageMatrix matrix1 = create_matrix("D:\\3\\11.png");
ImageMatrix matrix2 = create_matrix("D:\\3\\12.png");
Bitmap picture = new Bitmap(matrix1.picture);
using (var wrapper = new ImageWrapper(picture, true))
{
int x1 = 140;
int x2 = x1 + 25;
int y1 = 110;
int y2 = y1 + 25;
Random rnd=new Random();
StringBuilder sb = new StringBuilder();
DateTime dt1 = DateTime.Now;
Int64 min_res = 999999999999999999;
int min_dx = 0;
int min_dy = 0;
int k=0;
bool flag = false;
do
{
ResStruct res;
if (flag)
{
res = search(matrix1, matrix2, x1, y1, x2, y2, sb, min_dx, -100, min_dx, 100);
}
else
{
res = search(matrix1, matrix2, x1, y1, x2, y2, sb, -100, min_dy, 100, min_dy);
}
flag = !flag;
if (res.res < min_res)
{
min_res = res.res;
min_dx = res.dx;
min_dy = res.dy;
}
else
{
//Если у нас не получилось найти минимум меньше текущего (не приблизились к цели ни на сколько)
//то просто сдвинем оси на несколько случайных пикселей
if (flag) min_dy = min_dy + rnd.Next(10) - 5; else min_dx=min_dx + rnd.Next(10) - 5;
}
sb.AppendFormat("{0}; {1}; {2}; {3}; {4}\n", res.dx, res.dy, res.res, min_res, k);
k++;
} while (k < 1000 && min_res>=1);
DateTime dt2 = DateTime.Now;
MessageBox.Show(dt1.ToString() + " " + dt2.ToString());
System.IO.File.WriteAllText("D:\\3\\1.txt", sb.ToString());
for (int i = x1; i < x2; i++)
{
for (int j = y1; j < y2; j++)
{
int light1 = matrix1.matrix[i, j];
int light2 = matrix2.matrix[i + min_dx, j + min_dy];
int light = Math.Abs(light2 - light1);
wrapper[i, j] = Color.FromArgb(light, light, light);
}
}
pbImage.Image = picture;
}
}
Данный алгоритм нашел смещения за 12600 итераций (63 по 200):
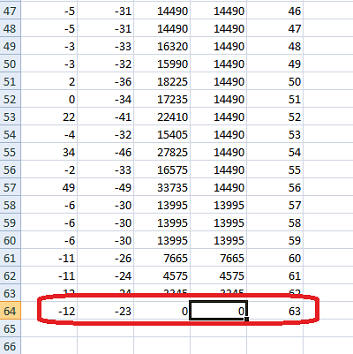
Это несколько быстрее. Правда, сам алгоритм — не самый оптимальный, его можно и дальше оптимизировать. Другой его недостаток: если неправильно выбрать начальные точки — зависнет и ничего не найдет. Например, выбрал сначала -100, -100, и поиск не получился.
Если эта тема вам будет интересна, то далее я расскажу о том, как еще улучшить этой алгоритм и устранить его недостатки, а также о том, как работать с ним на реальных, а не рисованных картинках.
