Алгоритм MiniMax. Использование минимакса в Unity на примере игры Поймай Овечку
Минимакс — популярный алгоритм для принятия решений в играх с нулевой суммой (один выиграл — другой проиграл). Казалось бы, раз он так популярен, то всё что можно было про него сказать уже сказано? Не совсем. Информация сильно раздроблена, иногда ошибочна, а найти какие-либо примеры в играх довольно сложно. Поэтому в этой статье я постараюсь прояснить процесс разработки ИИ на основе минимакса для игры «Поймай Овечку», разумеется все ссылки и код будут в конце статьи.
Зачем нужен Минимакс?
Как я и сказал ранее, этот алгоритм часто используется для игр с нулевой суммой, по другому говоря: когда выгода одного игрока, приводит к такой же невыгоде другого. К таким играм можно отнести: крестики-нолики, шахматы, шашки, и многие другие классические игры. В их числе игра Поймай Овечку.
Что из себя представляет игра?
Это интерпретация классической игры, которую как только не называют. Но суть одна: есть 1 фигура (овца) в одном конце доски и 4 фигуры (волки) в другом конце доски. Все фигуры ходят только по диагонали, овца может двигаться в любом направлении, волки только вперёд. Задача волков добиться того чтобы у овцы не осталось доступных ходов. Задача овцы в том, чтобы достигнуть противоположного края, или встать на линию с самым нижним волком игра, так как теперь волки её попросту не смогут схватить. Овцой управляется с помощью Минимакса, волками управляет игрок.

Что такое минимакс?
Минимакс это алгоритм принятия решений который основывается на том, что один участник будет выбирать наилучший ход для себя, то есть минимизировать шанс победы другого участника. Минимакс можно представить как рекурсивный метод который совершает ходы от имени обоих игроков, пока не достигнет определённый глубины (количества ходов 'вперёд'), после чего вычисляет насколько хороша текущая позиция (вес позиции). Такое происходит для всех возможных ходов, на выбранной глубине. Алгоритм вычисляет вес только на концах веток ходов (лепестках). Далее исходя из того что игрок будет пытаться выиграть, то есть свести вес хода ИИ к минимальному значению, можно будет найти вес всей ветке ходов. Поэтому каждый вызов метода минимакса можно разделить на максимизацию (ИИ) и минимизацию (игрок), это будет проще представить в виде дерева выбора последовательности ходов. Соответственно если указана очередь хода для игрока (минимизирующего), то узел получит минимальный вес из лепестков и наоборот, в случае ИИ (максимизирующего) он получит максимальный вес. Например, в случае если вес лепестков будет 3 и 5, а текущий узел во время хода ИИ (максимизирующего), то узел получит вес 5, поднимаясь выше по ветке ходов будут сравниваться уже два нижестоящих узла весом 5 и 9, так как ход игрока (минимизирующего), то узел получит минимальный вес — 5. По итогу результат выполнения алгоритма можно представить как обычное дерево, которое отражает оценки для всех возможных веток ходов и позволяет выбрать оптимальный ход.
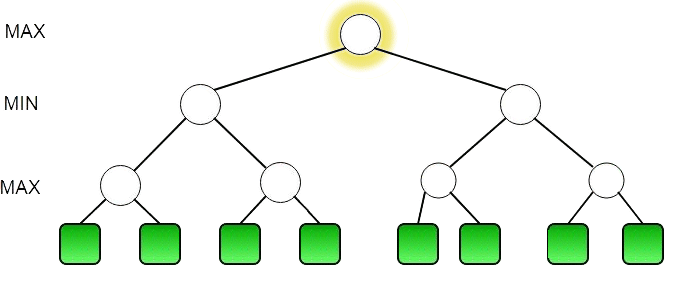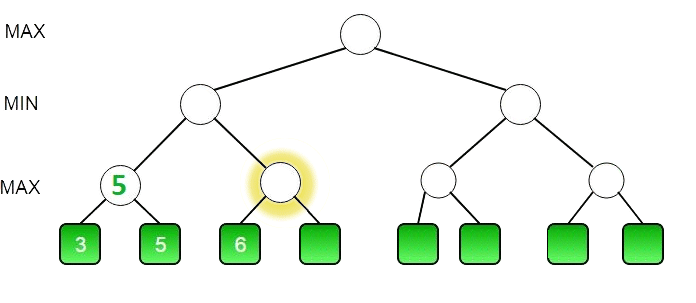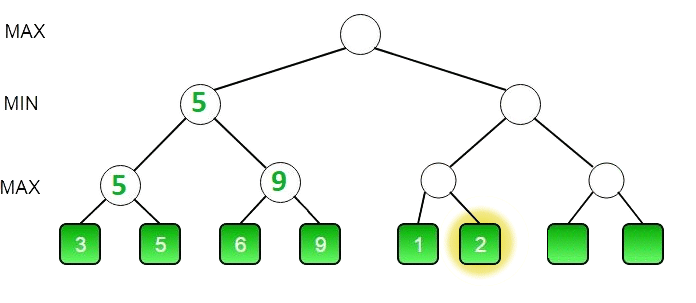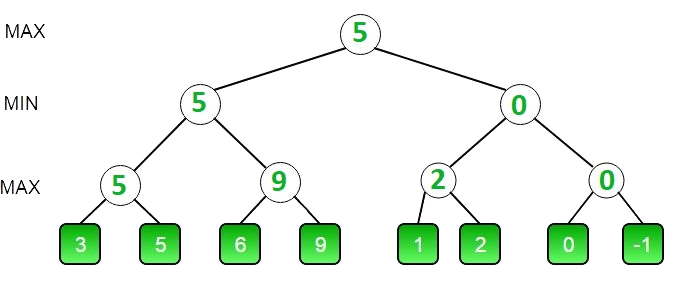
Работа алгоритма наглядно
Как это работает?
У нас есть метод «RunMinMax», который принимает в себя несколько обязательных аргументов:
bool AI — регулирует чей сейчас ход (ИИ если верно, игрок если ложь)
sbyte recursiveLevel — текущий уровень глубины (количество ходов совершённых ходов с момента вызова первичной функции)
SbyteVector2[] startPositions — массив структур которые содержат в себе позицию всех фигур на доске в виде sbyte значений (x, y)
необязательный аргумент sbyte aiLevel = 3 — регулирует уровень максимальной глубины для поиска ходов по формуле (aiLevel*2)
Метод проходится по всем возможным ходам для овцы (ИИ) и волков (игрока), которые представляют из себя массив структур, в случае если ход возможен, то текущая позиция обновляется и вновь вызывается функция минимакса в которую уже передаётся: ! AI — в случае если текущий вызов функции был совершён для ИИ (AI = true), следующий вызов будет для игрока (AI = false) и наоборот, recursiveLevel + 1 — так же увеличиваем уровень глубины для нового вызова, а так же новая позиция.
private short[] RunMinMax(bool AI, sbyte recursiveLevel, in SbyteVector2[] startPositions, in sbyte aiLevel = 3)
{
///если уровень глубины удовлетворяет условию, то вернуть вес
///нужно просчитать вес хода после того как волк сделает ход, то есть когда будет AI == true, до момента хода овцы
///так как ходы идут в порядке: овца - волк -овца - волк - просчёт, этого требует текущая реализацию просчёта веса хода
if ((recursiveLevel >= aiLevel * 2) && AI)
{
return new short[2] { -1, GetMoveWeight(startPositions) };
}
//объявляем переменные и так это простые типы их можно сразу инициализировать
short indexBestMove = -1;
short bestMoveWeight = -1500;
short badMoveWeight = 1500;
//сделать ход существом на все доступные ходы и вызвать на этих позициях RunMinMax()
//positions: 0-3 wolf, 4 sheep
for (int moveIndex = 0; moveIndex < (AI ? _possibleSheepMoves.Length : _possibleWolfMoves.Length * _wolfCount); moveIndex++)
{
SbyteVector2[] positions; //объявляем позицию сейчас, иницилизируем только если проходит проверку на CanMove()
if (AI)
{
//делаем ход за существо и создаём его новую позицию
SbyteVector2 newSheepPosition = startPositions[4] + _possibleSheepMoves[moveIndex];
//проверяем можно ли сделать ход на новую позицию
if (!CanMove(newSheepPosition, startPositions)) continue;
///создаём "клон" массива позиций.
///используется сторонний метод так как Array.Clone() выделяет намного больше мусора из за множества приведений типов,
///используемый метод в свою очередь создаёт новый массив который заполняет структурами с данными как и во входном массиве.
positions = SbyteVector2.CloneSbyteVectorArray(startPositions);
//устанавливаем новую позицию для овцы
positions[4] = newSheepPosition;
}
else
{
//получаем индекс волка в массиве позиций
int wolfIndex = moveIndex / _possibleWolfMoves.Length;
//делаем ход за существо и создаём его новую позицию
SbyteVector2 newWolfPosition = startPositions[wolfIndex] + _possibleWolfMoves[moveIndex % _possibleWolfMoves.Length];
if (!CanMove(newWolfPosition, startPositions)) continue;
positions = SbyteVector2.CloneSbyteVectorArray(startPositions);
//устанавливаем новую позицию для волка
positions[wolfIndex] = newWolfPosition;
}
//вызвать метод, передать в него новую позицию и увеличить уровень рекурсии
short moveWeight = RunMinMax(!AI, (sbyte)(recursiveLevel + 1),
positions, aiLevel)[1];
//на нулевой рекурсии если вес больше лучшего то установить этот ход как лучший для овцы
if (recursiveLevel <= 0 && moveWeight >= bestMoveWeight)
{
//немного случайности если веса одинаковые
if (moveWeight == bestMoveWeight)
{
if (GetRandomBool())
{
indexBestMove = (short)moveIndex;
}
}
else
{
indexBestMove = (short)moveIndex;
}
}
//установить лучший и худший вес хода
if (moveWeight > bestMoveWeight) bestMoveWeight = moveWeight;
if (moveWeight < badMoveWeight) badMoveWeight = moveWeight;
}
//если овца то она выберет лучший ход для себя, если волк то он выберет худший ход для овцы
return AI ? new short[2] { indexBestMove, bestMoveWeight } : new short[2] { -1, badMoveWeight };
}Так происходит вплоть до лепестков, где вызывается метод просчёта веса — «GetMoveWeight», который возвращает вес текущей позиции. Далее результат метода минимакса возвращается в формате массива из двух элементов, где 0 индекс — индекс, для массива с ходами, лучшего первого хода, а 1 — вес хода, в вызывающий метод. После того как все цепочки ходов найдены и просчитаны, метод, который был вызван напрямую, а не рекурсивно (нулевой вызов функции), возвращает массив в котором уже для 0 индекса будет указан номер лучшего хода для овцы (ИИ).
Сам же метод «GetMoveWeight» представляет собой цепочку расчётов, которые на основе позиции SbyteVector2[] positions, а так же на основе значений в enum _moveWeight возвращает short значения веса для текущей позиции овцы. Обычно для вычислений веса хода используют только условие победы и проигрыша. Однако в случае если нельзя сразу просчитать на такую глубину, где можно найти победную цепочку ходов или если победа невозможна без ошибки игрока, тогда необходимо дополнительное условие. В моём случае первая прибавка веса (5 строка) является дополнительным условием, на 23 строке прибавка является условием победы, а на 39 — условием поражения.
private enum _moveWeight : sbyte
{
VerySmall = 1,
Small = 2,
Medium = 3,
Normal = 4,
Big = 6,
VeryBig = 8,
ExstraBig = 12,
Max = 127
}private short GetMoveWeight(in SbyteVector2[] positions)
{
short moveWeight = 0;
//прибавить вес тем больше, чем ближе овца к краю доски
moveWeight += (short)((_mapHeight - 1 - positions[4].y) * (sbyte)_moveWeight.Normal);
bool sheepLover = true;
for (sbyte i = 0; i < _wolfCount; i++)
{
//если волк ниже овцы
if (positions[i].y < positions[4].y)
{
sheepLover = false;
break;
}
}
///если клетка на краю доски или овца на одной линии с самым нижни волком,
///то дать максимальный вес для этого шага, так как это условие победы
if (positions[4].y == 0 || sheepLover)
{
moveWeight += (sbyte)_moveWeight.Max;
}
//посчитать клетки для возможных ходов
sbyte moveCell = 0;
for (sbyte sheepMoveIndex = 0; sheepMoveIndex < _possibleSheepMoves.Length; sheepMoveIndex++)
{
if (!CanMove(positions[4] + _possibleSheepMoves[sheepMoveIndex], positions)) continue;
moveCell++;
}
//если ходов нет то сильно убавить вес хода, так как это означает поражение для овцы
if (moveCell == 0)
{
moveWeight -= (sbyte)_moveWeight.Max;
}
return moveWeight;
}Теперь можно перейти к методу «CanMove». Метод принимает два обязательных аргумента: новую позицию для хода в форме структуры, а так же массив структур которые представляют собой текущее положение персонажей. Метод возвращает истину если ход на новую позицию возможен, ложь в ином случае. Для того чтобы понять возможен ли ход на новую позицию нужно проверить: находятся ли координаты newPosition на доске, а так же не занято ли это место другим существом.
private bool CanMove(in SbyteVector2 newPosition, in SbyteVector2[] position)
{
//вернуть false если x или y находится за границей карты
if (!(newPosition.x < _mapWidth && newPosition.y < _mapHeight && newPosition.x >= 0 && newPosition.y >= 0)) return false;
//проверяем есть ли какое существо на новой позиции
for (sbyte i = 0; i < position.Length; i++)
{
if (position[i] == newPosition) return false;
}
return true;
}В результате вызова метода «RunMinMax» возвращается массив из 2 значений: индекс лучшего хода овцы и вес этого хода. Индекс хода можно использовать чтобы получить из массива структур _possibleSheepMoves нужную структуру которая будет обозначать ход. Соответственно уже после это можно преобразовать в обычный Vector2 и передвинуть существо на это значение относительно текущей позиции.
_possibleSheepMoves = new SbyteVector2[]
{
new SbyteVector2(-1, -1),
new SbyteVector2(+1, -1),
new SbyteVector2(-1, +1),
new SbyteVector2(+1, +1)
};
_possibleWolfMoves = new SbyteVector2[]
{
new SbyteVector2(-1, +1),
new SbyteVector2(+1, +1)
};Приведённого выше кода достаточно для реализации самого алгоритма минимакса, но если использовать это в текущем виде, можно разочароваться.
Первая проблема Минимакса
Алгоритм минимакса сам по себе довольно медленный и ресурсозатратный. Ведь возможных комбинаций ходов, казалось бы на такой маленькой доске 8×8, миллионы и это при том, что всего возможных состояний фигур на доске только 4368. Рассчитать максимально возможное количество комбинаций ходов можно по формуле:
Тут конечно стоит заметить что формула верна только в случае когда у всех существ доступны все ходы, чего в реальности конечно не будет. Но даже так количество возможных ходов поражает, а это только просчёт на 5 очереди шагов вперёд.
Использование Альфа-Бета отсечения
Альфа-Бета отсечение — алгоритм который позволяет без влияния на качество вычислений существенно сократить количество просчётов. Для сравнения можно посмотреть сколько раз происходит вычисление веса хода (вызов метода «GetMoveWeight») без использования Альфа-Бета отсечения и с ним. Без отсечения метод вызывается до 340000 раз, используя Альфа-Бета отсечение до 6500 раз.
Почему же такая огромная разница и почему это не влияет на качество вычислений?
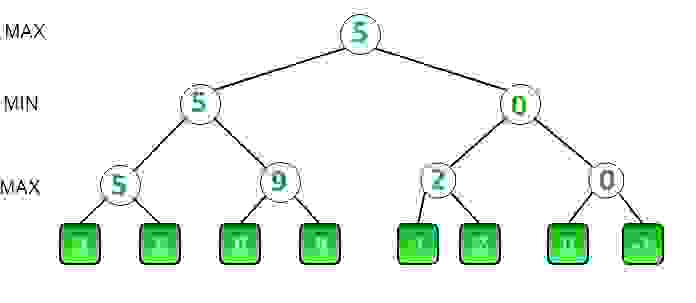
Исходя из того, что каждая глубина делится на максимизацию (ИИ) и минимизацию (игрок), можно использовать этот принцип, чтобы сократить количество вычислений. Для примера возьмём узел с весом 5 на глубине минимизации. Нужно вычислить его вес, для этого необходимо вычислить вес нижестоящих узлов, алгоритм вычисляет вес лепестков первого узла и устанавливает вес узла 5, теперь можно вычислить вес лепестка другого нижестоящего узла, который составит 6. Так как узел, которому принадлежит этот лепесток, находится на глубине максимизации, мы точно знаем что будет выбран лепесток с наибольшим весом, поэтому можно сразу предположить что вес этого узла будет 6 или больше. Так как вышестоящий узел на глубине минимизации, то в любом случае будет выбран узел с наименьшим весом, а так как вес нижестоящего узла уже как минимум равен 6, то рассчитывать последний его лепесток не имеет смысла, так как другой нижестоящий узел имеет вес 5, поэтому будет выбран он. Такой процесс повторяется во всех узлах и позволяет отбросить ветки, которые не повлияют на результат. Для этого выделяются два понятия: Альфа — максимальный вес узла, который максимизирующий игрок (ИИ) может достичь; и Бета — минимальный вес узла, который может достичь минимизирующий игрок (игрок). Значение Альфы обновляется в момент хода максимизирующего (ИИ), беты — минимизирующего (игрок). Изначально Альфа представляет собой значение минимально возможного веса хода, обычно отрицательную бесконечность, Бета в свою очередь наоборот, представляет положительную бесконечность. В случае который представлен на иллюстрации, в момент когда уже вычислен лепесток с весом 6, для вышестоящего узла Альфа = 6, так как значение переменной было обновлено после вычисления веса лепестка, Бета = 5, так как это значение было передано из вышестоящего узла, который находится на уровне минимизации и установил это значение в момент когда был вычислен вес первого его нижестоящего узла с весом 5. Теперь условие 6>=5 становится верным и последующие лепестки для данного узла найдены не будут.
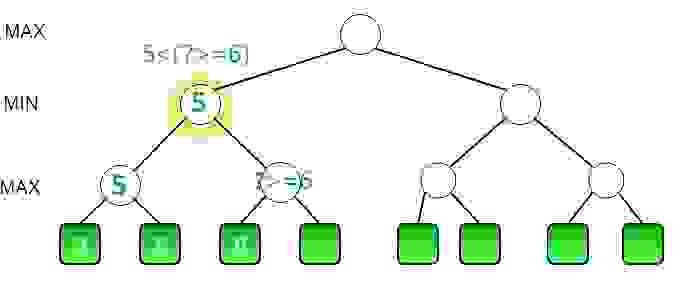
Тут так же стоит заметить некоторые моменты относительно использования Альфа-Бета отсечения: эффективность алгоритма многократно увеличивается с ростом максимальной рекурсии; для эффективной работы алгоритма наилучшие ходы всех существ должны просчитываться первыми, в случае моей реализации Минимакса достаточно установить лучшие ходы на первые позиции в массиве с ходами, в случае с овцой это будут ходы к другому краю доски, то есть те где y = -1.
Реализация в коде
Итак, когда цель понятна, осталось только перенести это в код. Для этого необходимо в метод «RunMinMax» добавить 2 новые переменные, типа short, как необязательный аргумент: «bestMoveWeightAlpha» — вес наилучшего хода овцы, значение по умолчанию = -1500, «badMoveWeightBeta» — наименьший вес хода овцы, значение по умолчанию = 1500, использовать максимальное число для этого типа тут избыточно, так как я точно знаю что вес хода не выйдет за порог этих значений. Значения переменных необходимо передавать при рекурсивном вызове метода. В том же методе в теле цикла добавить условие что цикл будет остановлен в случае если «bestMoveWeightAlpha >= badMoveWeightBeta». Теперь алгоритм минимакса с Альфа-Бета отсечением будет выглядеть так:
private short[] RunMinMax(bool AI, sbyte recursiveLevel, in SbyteVector2[] startPositions, short bestMoveWeightAlpha = -1500, short badMoveWeightBeta = 1500, in sbyte aiLevel = 3)
{
///если уровень глубины удовлетворяет условию, то вернуть вес
///нужно просчитать вес хода после того как волк сделает ход, то есть когда будет AI == true, до момента хода овцы
///так как ходы идут в порядке: овца - волк -овца - волк - просчёт, этого требует текущая реализацию просчёта веса хода
if ((recursiveLevel >= aiLevel * 2) && AI)
{
return new short[2] { -1, GetMoveWeight(startPositions) };
}
//объявляем переменные и так это простые типы их можно сразу инициализировать
short indexBestMove = -1;
short bestMoveWeight = -1500;
short badMoveWeight = 1500;
//сделать ход существом на все доступные ходы и вызвать на этих позициях RunMinMax()
//positions: 0-3 wolf, 4 sheep
for (int moveIndex = 0; moveIndex < (AI ? _possibleSheepMoves.Length : _possibleWolfMoves.Length * _wolfCount); moveIndex++)
{
SbyteVector2[] positions; //объявляем позицию сейчас, иницилизируем только если проходит проверку на CanMove()
if (AI)
{
//делаем ход за существо и создаём его новую позицию
SbyteVector2 newSheepPosition = startPositions[4] + _possibleSheepMoves[moveIndex];
//проверяем можно ли сделать ход на новую позицию
if (!CanMove(newSheepPosition, startPositions)) continue;
///создаём "клон" массива позиций.
///используется сторонний метод так как Array.Clone() выделяет намного больше мусора из за множества приведений типов,
///используемый метод в свою очередь создаёт новый массив который заполняет структурами с данными как и во входном массиве.
positions = SbyteVector2.CloneSbyteVectorArray(startPositions);
//устанавливаем новую позицию для овцы
positions[4] = newSheepPosition;
}
else
{
//получаем индекс волка в массиве позиций
int wolfIndex = moveIndex / _possibleWolfMoves.Length;
//делаем ход за существо и создаём его новую позицию
SbyteVector2 newWolfPosition = startPositions[wolfIndex] + _possibleWolfMoves[moveIndex % _possibleWolfMoves.Length];
if (!CanMove(newWolfPosition, startPositions)) continue;
positions = SbyteVector2.CloneSbyteVectorArray(startPositions);
//устанавливаем новую позицию для волка
positions[wolfIndex] = newWolfPosition;
}
//вызвать метод, передать в него новую позицию и увеличить уровень рекурсии
short moveWeight = RunMinMax(!AI, (sbyte)(recursiveLevel + 1),
positions, bestMoveWeightAlpha, badMoveWeightBeta, aiLevel)[1];
//обновить лучший худший вес для альфа бета отсечения
if (AI)
{
//если овечка то она выберет лучший ход для себя
if (moveWeight > bestMoveWeightAlpha) bestMoveWeightAlpha = moveWeight;
}
else
{
//если волк то он выберет худший ход для овцы
if (moveWeight < badMoveWeightBeta) badMoveWeightBeta = moveWeight;
}
//на нулевой рекурсии если вес больше лучшего то установить этот ход как лучший для овцы
if (recursiveLevel <= 0 && moveWeight >= bestMoveWeight)
{
//немного случайности если веса одинаковые
if (moveWeight == bestMoveWeight)
{
if (GetRandomBool())
{
indexBestMove = (short)moveIndex;
}
}
else
{
indexBestMove = (short)moveIndex;
}
}
//установить лучший и худший вес хода
if (moveWeight > bestMoveWeight) bestMoveWeight = moveWeight;
if (moveWeight < badMoveWeight) badMoveWeight = moveWeight;
//альфа-бета отсечение
if (bestMoveWeightAlpha >= badMoveWeightBeta)
{
break;
}
}
//если овца то она выберет лучший ход для себя, если волк то он выберет худший ход для овцы
return AI ? new short[2] { indexBestMove, bestMoveWeight } : new short[2] { -1, badMoveWeight };
}По итогу мы получаем алгоритм Минимакса, который к тому же работает относительно быстро, благодаря оптимизации в виде Альфа-Бета отсечения. Однако если установить значение aiLevel отличным от 1, то ИИ не сильно будет пытаться выиграть, а в основном ходить кругами с одной клетки на другую, находясь в шаге от победы.
Вторая проблема Минимакса
Текущая реализация алгоритма вычисляет вес хода только на определённом уровне рекурсии, который должен соответствовать условию:»(recursiveLevel >= aiLevel * 2) && AI». Таким образом если aiLevel будет равен 2, а ИИ находится в шаге от победы, то он просто не сможет сделать победный шаг, так как не сможет его просчитать. В свою очередь ИИ встанет на клетку которая находится рядом с победной клеткой, после есть два варианта: либо будет выбрана цепочка ходов в виде: ход на победную клетку — ход назад, либо: ход назад — ход на клетку рядом с победной. То есть для того чтобы ИИ мог сделать завещающий победный ход aiLevel должен быть равен 1, но при этом ИИ так же должен просматривать ходы наперёд, для этого aiLevel должен быть как можно больше.
Итеративное углубление
Решить эту проблему можно если в теле класса объявить переменную «sbyte _aiLevel» которая будет отражать максимальный уровень аргумента «aiLevel» в методе «RunMinMax», сам же метод необходимо вызывать со значением «aiLevel» равным 1, а затем постепенно увеличивать, до значение переменной »_aiLevel». Таким образом получиться некоторое количество первичных вызовов метода «RunMinMax» и соответственно такое же количество результатов выполнения метода, это количество соответствует значению »_aiLevel». После можно выбрать лучший результат и на его основе сделать ход. тут так же стоит заметить что если значение «aiLevel» будет большим, а партия на стадии завершения где возможных ходов мало, то алгоритм Минимакса просто не сможет сделать ход и соответственно посчитать вес хода, в таком случае в качестве результата он вернёт массив {-1, -1500} или {-1, 1500}, где индекс 1 является границей веса хода. Поэтому необходимо пропускать и не учитывать такие результаты.
private sbyte GetIndexBestMove()
{
sbyte bestMoveIndex = -1;
short bestMoveWeight = -1500;
///итеративное углубление
///постепенно увеличиваем максимальный уровень ии и выбираем лучший ход
for (sbyte i = 1; i <= _aiLevel; i++)
{
short[] result = RunMinMax(true, 0, _startPositionsOnMap, aiLevel: i);
///в случае если вес равен границе диапазона веса, это значит что ходы кончились раньше чем был
///получен вес, необходиммо игнорировать эти результаты
if (result[1] != 1500 && result[1] != -1500) break;
//если вес хода больше лучшего, то выбрать его.
if (result[1] > bestMoveWeight)
{
bestMoveIndex = (sbyte)result[0];
bestMoveWeight = result[1];
}
}
return bestMoveIndex;
}Теперь достаточно установить желаемое значение для »_aiLevel» и вызвать метод «GetIndexBestMove» который вернёт индекс лучшего хода.
Проблемы использования Минимакса
Скорость. Даже с учётом использования Альфа-бета отсечения скорость работы алгоритма не радует. Что можно с этим сделать? Помимо Альфа-Бета отсечения можно использовать другие алгоритмы оптимизации. Можно сохранять позиции полученные в ходе выполнения выполнения итеративного углубления и использовать их для вызова метода «RunMinMax», с более высоким значением «aiLevel», вместо новых просчётов с нуля. Так же можно использовать результаты предыдущего хода если получилось предугадать какой ход сделал игрок.
Сложность отладки. Минимакс является рекурсивным алгоритмом и только это сильно увеличивает сложность отладки. Так же если где то в реализации алгоритма ошибка, узнать об этом до её фактического обнаружения в коде, практически невозможно: алгоритм может продолжить выдавать ходы, которые даже могут быть логически хорошими, а каким либо образом проверить правда ли совершённый ход является наилучшем — не получиться.
Нарастающая ошибка. Логика Минимакса в том что ИИ делает наилучший ход для себя и предполагается что игрок будет делать наихудший ход для ИИ, что в корне не верно. Понятное дело человек ошибается, а вместе с тем падает точность алгоритма при увеличении глубины.
