AES против осциллографа14.12.2020 22:47

Слово «хакер» обрело свое нынешнее звучание лишь во второй половине XX века благодаря журналистам. Изначально хакерами именовали специалистов, обладающих обширными знаниями в области компьютерных технологий и умеющих виртуозно применять их. Именно о деятельности одной из групп таких хакеров пойдет речь в данной статье.

Введение

В 2007 году компания Nvidia представила первую версию CUDA — программно-аппаратную архитектуру параллельных вычислений, позволяющую использовать графические ускорители для большего класса задач, нежели только рендеринг изображений. Переведя свои графические процессоры из разряда GPU в разряд GPGPU (General Purpose GPU), Nvidia сделала массивно-параллельные вычисления доступнее для широкого круга задач. В частности, видеопроцессоры оказались применимы к задачам шифрования, и разработчики криптографических библиотек воспользовались возможностью ускорить вычисления. К сожалению, как и любые электронные устройства, видеокарты излучают электромагнитные волны, и характер этого излучения зависит от конкретных действий графического процессора. Пристальное наблюдение за таким излучением позволило группе ученых из UCAS взломать шифр AES, узнав значение секретного ключа.

Краткое напоминание

Прежде чем перейти непосредственно к атаке, нелишним будет вспомнить основы CUDA и AES:

CUDA

CUDA (Compute Unified Device Architecture) — это программно-аппаратная архитектура параллельных вычислений, предложенная компанией Nvidia для своих графических процессоров общего назначения. Давайте посмотрим на CUDA с двух различных ракурсов.

С точки зрения программиста

При написании программ, использующих CUDA, программист имеет дело со следующими сущностями:

ядро (kernel) — функция, исполняемая на GPGPU;
сетка (grid) — группа потоков, исполняющих код одного ядра;
блок (block) — составляющая сетки. Каждый блок --- это совокупность потоков и некоторого количества общей памяти;
нить исполнения (поток, thread) — составляющая блока.

Программист сам определяет число потоков в блоке и блоков в сетке, исходя из особенностей решаемой задачи. Подробнее про программирование с использованием CUDA можно узнать здесь и тут.

Для эффективного управления описанными сущностями необходимо понимать, как они связаны с аппаратной реализацией GPGPU.

С точки зрения CUDA

С точки зрения CUDA, GPGPU выглядит следующим образом (на этот раз движемся снизу вверх):

Скалярный процессор (Scalar Processor, SP) — ядро, исполняющее единомоментно один поток;
Потоковый мультипроцессор (Streaming Multiprocessor, SM) — совокупность нескольких SP, разделяемой памяти, нескольких 32-байтных регистров и общего блока формирования команд (Instruction Unit). Также SM обладает L1-кэшем, общим для всех SP. При назначении работ планировщиком каждому SM достается свой набор блоков сетки, исполняемых по очереди;
GPU — массив из SM, по которому распределяются блоки.

Ещё одна важная особенность работы GPGPU, не выраженная столь явно, связана с исполнением блоков. Каждый блок исполняется группами по 32 нити (warp). Внутри такой группы все потоки выполняют одну инструкцию над разными данными, то есть реализуют так называемую SIMT-архитектуру (Single Instruction Multiple Threads).

Более полное описание архитектуры GPGPU можно найти в Белой книге, на Вики и в официальной документации. Полезным может показаться и это обсуждение.

Для понимания атаки предоставленного описания должно быть достаточно.

AES

Advanced Encryption Standard (AES), также известный как Rijndael — популярный симметричный алгоритм блочного шифрования. Он оперирует блоками данных длины 128 бит при длине ключа 128, 192 или 256 бит. Так как атака демонстрировалась на шифровании с длиной ключа 128 бит, пока уберем прочие размеры из рассмотрения и сфокусируемся на алгоритме для длины ключа 128 бит.

AES-128 представляет входной блок текста в виде матрицы S размером 4 на 4 байта, называемой состоянием (state), и 11 раз последовательно применяет к нему следующие операции:

SubBytes — замена каждого из байтов в матрице состояния на значения, указанные в таблице замен SBox. Это таблица размером 16 на 16, в ячейках которой записаны новые значения байтов. Замена производится по простому правилу: представляя байт в виде $\{x, y\}$ , где и — шестнадцатеричные цифры, мы заменяем его на значение, лежащее на перечесении -ой строки и -ого столбца таблицы SBox. В частности, при построчном хранении таблицы в памяти (Row-Major Ordering) искомое значение будет смещено на позиций от начала таблицы.
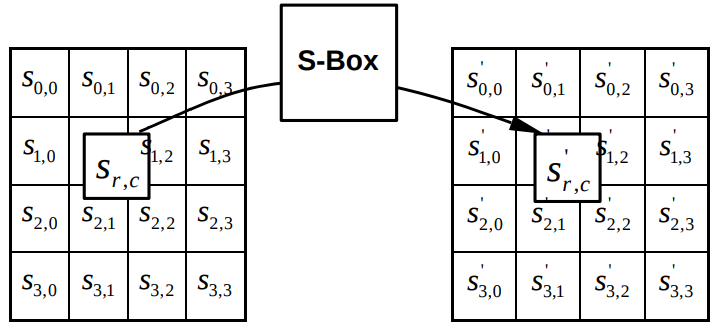
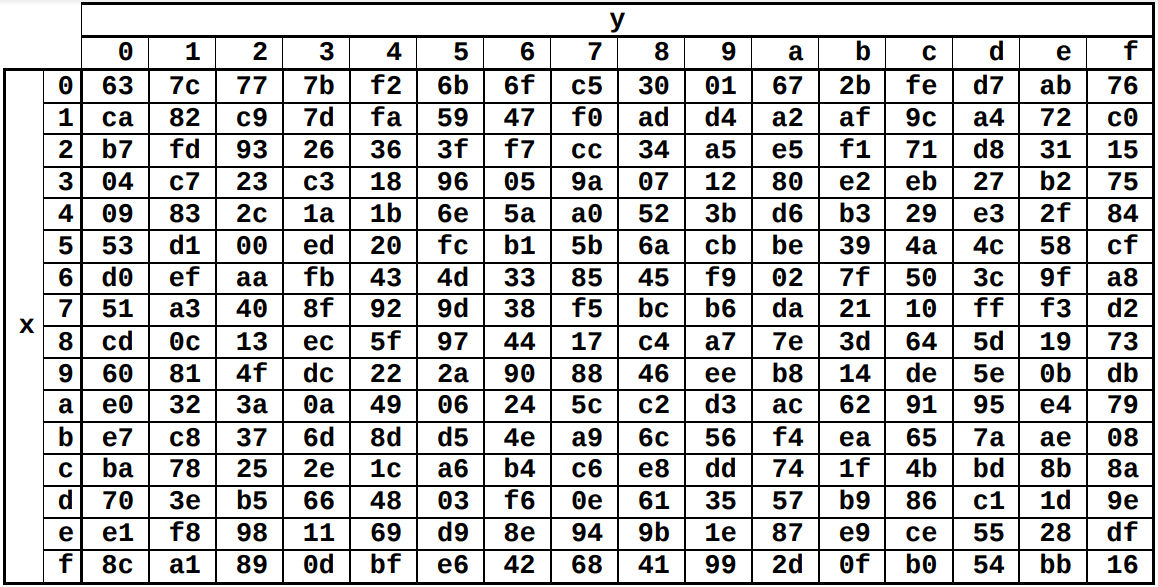
Нам не обязательно понимать, как именно строится таблица замен, поскольку значения в ней постоянны и уже вычислены и явно указаны в стандарте. В целях сокращения общего времени шифрования часто используется уже готовая таблица SBox, которую мы будем называть SBoxLUT (Look Up Table).
ShiftRows — циклический сдвиг строк матрицы состояния. Первая строка не сдвигается, вторая сдвигается на одну позицию, третья на две и четвертая на три.
MixColumns — умножение на фиксированную матрицу, осуществляющее линейные преобразования над стоблцами — сложения столбцов и умножение столбца на константу. Как и в случае с SBox, принцип получения матрицы мы оставим за кадром, поскольку вычислять каждый раз ее не нужно.
AddRoundKey — поэлементное прибавление матрицы RounKey того же размера 4 на 4, содержащей раундовый ключ. Перед началом шифрования алгоритм AES генерирует так называемое «расписание ключей» — набор из 11 матриц, называемых раундовыми ключами, по одной на каждый этап шифрования. Процесс генерации расписания описывается вспомогательной операцией KeyExpansion на основе изначального секретного ключа.

Как уже было замечено выше, описанные преобразования применяются 11 раз. Каждый такой цикл называется раундом. В действительности, 11-ый раунд несколько отличается от предыдущих десяти, так что алгоритм можно представить в следующем виде:

AddRoundKey(0)

for (i = 1; i <= 10; i += 1) {
    SubBytes()
    ShiftRows()
    MixColumns()
    AddRoundKey(i)
}

SubBytes()
ShiftRows()
AddRoundKey(11)

В качестве финального замечания необходимо отметить, что все сложения и умножения производятся в конечном поле GF(2^8) . Простыми словами, сложение двух байтов эквивалентно применению к ним операции ИСКЛЮЧАЮЩЕЕ-ИЛИ, которую мы будем обозначать символом $\oplus$ .

Приведение всех тонкостей и нюансов, равно как и подробного разбора каждого из шагов алгоритма, выходит за рамки данной статьи, однако исчерпывающее описание может быть найдено в стандарте. Альтернативные объяснения с примерами, а также множество программных реализаций могут быть найдены в на Хабре здесь и здесь.

Говоря об AES, нельзя не упомянуть пьесу про AES, в частности — акт третий, сцена вторая.

Описание атаки

Будем рассматривать процесс шифрования сообщения длины 32×16 байтов, при котором задача является чрезвычайно параллельной (Embarrassingly Parallel): для шифрования будет зайдествована единственная группа потоков, каждый из которых будет заниматься шифрованием собственного блока данных. Предположим, что злоумышленник может шифровать любой текст и читать полученный шифротекст, а также обладает физическим доступом к атакуемой видеокарте.

Описываемая атака принадлежит к классу атак по стороннему каналу. В процессе шифрования видеокарта испускает электромагнитное излучение, зависящее от используемых в работе величин. Ниже приведен краткий план атаки.

Локализовать точку над видеокартой, испускающей информативный сигнал;
Подготовить текст для шифрования;
Запустить процедуру шифрования, измерить поле в выбранной точке;
Определить значение секретного ключа, используемого на финальном раунде шифрования, вычисляя по очереди каждый из 16 байтов:
1. Выбрать байт с номером ;
2. Перебрать возможные 256 значений $k^{guess}_l$ :
  1. Рассчитать промежуточные значения и для каждого $k^{guess}_l$ ;
  2. Разделить полученные в пункте 3 измерения на две группы в соответствии с и ;
  3. Рассчитать величину $\Delta$ , соответствующую данному $k^{guess}_l$ ;
3. Определить искомое значение байта как $k_l^{guess}$ , на котором достигается наибольшее значение $\Delta$ ;
Зная все байты последнего раундового ключа, восстановить изначальный секретный ключ.

В приведенном плане используются обозначения, которые будут введены позже. Ознакомившись с планом, давайте перейдем к подробному рассмотрению шагов, после которых предлагаемое описание станет понятнее.

Физические основы

В основе атаки лежит наблюдение за ближним полем — электромагнитным излучением в области, удаленной от источника не более, чем на $1/2\pi$ длины волны. Авторы заметили, что существует явная связь между операциями, выполняемыми GPGPU, и видом электромагнитного поля, излучаемого видеокартой. Результатом одного измерения является набор точек, снятых с электронного осциллографа и характеризующих зависимость напряжения исследуемого поля от времени для последнего раунда шифрования. Каждое такое измерение имеет одинаковое число точек, синхронизированных по времени. В дальнейшем мы будем называть эти точки отсчетами.

Отдельным вопросом является определение места измерений. Печатные платы, коими и являются GPGPU, имеют в своем составе сотни электронных компонент, однако не все они являются источниками утечек информации. Авторы предлагают рассматривать в качестве источников утечек лишь сам чип и емкости на обратной его стороне, что значительно сужает область поиска. Далее в цикле запускается процесс шифрования одного и того же текста и наблюдается вид сигнала на осциллографе в различных точках вблизи GPGPU. Как только злоумышленник увидит повторяющийся сигнал, он может прекратить поиски и проводить дальнейшие измерения в этой точке.

Кэш-коллизии

В качестве операции, надежно генерирующей различимые сигналы, авторы рассматривают одновременную кэш-коллизию (Simultaneous Cache Collision, SCC). В процессе исполнения все потоки, принадлежащие одной warp-группе, могут обратиться к данным, находящимся в одной (происходит SCC) или различных (SCC не происходит) кэш-линиях. При этом генерируемый электромагнитный сигнал будет различаться.

Заметим, что длина кэш-линии GPGPU архитектуры Fermi, рассматриваемой в данной работе, составляет 128 байтов. Размер же таблицы SBoxLUT, используемой на этапе SubBytes, составляет 256 байтов, то есть для размещения таблицы в памяти требуется две кеш-линии, по одной на первую и вторую половину. Отсюда же видно, что наличие SCC говорит об обращении всеми потоками к SBoxLUT по индексам либо из диапазона $D_1 = \{0~..~127\}$ , либо из $D_2 = \{128~..~255\}$ .

Атака

Обработка данных утечки

Рассмотрим последний раунд шифрования текста. Он описывается следующим уравнением:

$c_l = SBox(r_l) \oplus k_l, ~l \in \{0, 1, ..., 15\},$

где $c_{l}$ и $k_{l}$ — -ый байт шифротекста и -ый байт последнего раундового ключа, соответственно, а $r_{l}$ — некоторое промежуточное значение. Злоумышленник может предположить, что использовался ключ $k^{guess}$ . В таком случае, зная $c_{l}$ , можно найти величину промежуточного байта $r_{l}$ :

$r_l = InvSBox(c_l \oplus k^{guess}_l),~l \in \{0, 1, ..., 15\},$

где InvSBox — таблица обратной замены, известная из стандарта и обладающая свойством InvSBox( SBox(i) ) = i , а $k^{guess}_l$ — -ый байт предполагаемого ключа $k^{guess}$ . Мы предположили, что злоумышленник может шифровать любой текст. В частности, он может заготовить текст, состоящий всего из двух типов блоков. При шифровании такого текста значения -го байта $r_{l}$ , полученные каждым из потоков, будут принимать всего два различных значения: $r_{l}^1$ и $r_{l}^2$ . Будучи использованными в качестве индексов для обращения к таблице SBoxLUT, они либо приведут к кэш-коллизии, либо нет. Зная $r_{l}^1$ и $r_{l}^2$ , отличить эти случаи несложно: коллизия происходит только когда обе величины принадлежат одному диапазону: D_1 или D_2 .

Следующим шагом злоумышленника будет разделение полученных измерений ЭМ-поля на две группы G_1 и G_2 согласно вычисленным r_l^1 и r_l^2 : где коллизии были и где их не было. Формально это можно записать так:

$G_1 = \{ \vec{T_i}~|~(r_l^1 \in D_1~\text{и}~r_l^2 \in D_1)~\text{или}~(r_l^1 \in D_2~\text{и}~r_l^2 \in D_2) \},$ $G_2 = \{ \vec{T_i}~|~(r_l^1 \in D_1~\text{и}~r_l^2 \in D_2)~\text{или}~(r_l^1 \in D_2~\text{и}~r_l^2 \in D_1) \},$

где под $\vec{T_i}$ понимается набор точек, соответствующих одному раунду шифрования.

Авторы заметили, что сигналы, соответствующие наличию коллизии, похожи между собой, но сильно отличаются от сигналов в её отсутствие, и наоборот. Соответственно, можно рассмотреть величину

$\vec{\Delta} = \left| \frac{1}{n_1}\sum_{\vec{T_i} \in G_1} \vec{T_i} - \frac{1}{n_2}\sum_{\vec{T_i} \in G_2} \vec{T_i} \right|,$

показывающую, насколько сильно отличаются средние значения сигналов, помещенных в множества G_1 и G_2 . Под операцией суммирования здесь понимается сложение соответствующих отсчетов сигналов, а под переменными n_1 и n_2 — мощности множеств G_1 и G_2 , соответственно. Здесь необходимо отметить, что, поскольку разбиение сигналов на группы зависит от $k^{guess}_l$ , то и $\vec{\Delta}$ является функцией от $k^{guess}_l$ : $\vec{\Delta} = \vec{\Delta}(k^{guess}_l)$ .

Восстановление ключа

Если предполагаемый ключ $k^{guess}$ совпал с ключом, использованным для шифрования, то восстановленные значения r_l^1 и r_l^2 совпадут с действительно использованными при шифровании, и злоумышленник верно распределит сигналы по группам. Наоборот, при ошибочном выборе $k_{guess}$ разделение на группы по вычисленным промежуточным значениям r_l^1 и r_l^2 приведет к равномерно перемешанным сигналам. При этом значения компонент $\vec{\Delta}(k^{guess}_l)$ в первом случае будут заметно превосходить соответствующие компоненты во втором. Таким образом, для вычисления -го байта секретного ключа злоумышленнику достаточно будет перебрать 256 возможных значений и выбрать то, при котором $\vec{\Delta}(k^{guess}_l)$ принимает наибольшее значение. Делать это авторы предлагают следующим образом:

$\DeclareMathOperator*{\argmax}{argmax} k_l^{correct} = \argmax_k \left( \max_{k\in\{0~..~255\}} \left( \max_{i} \Delta_i \right) \right),$

где $\Delta_i$ — -я координата вектора $\vec{\Delta}$ . Формула легко интерпретируется: каждому из значений соответствует вектор $\vec{\Delta}(k)$ с наибольшей -ой координатой. Запомнив абсолютное значение этой координаты, из полученных 256 значений нужно снова выбрать наибольшее. Соответствующее ему принимается за искомый байт ключа $k^{correct}_l$ . Повторив описанную процедуру для каждого $l \in \{ 0~..~15 \}$ , злоумышленник сможет восстановить полное значение последнего раундового ключа в расписании. Алгоритм восстановления исходного секретного ключа, используемого при генерации расписания, из последнего раундового ключа для алгоритма AES-128 известен и уже обсуждался здесь или здесь.

В работе авторы показывают, что для успешного восстановления ключа таким методом достаточно собрать данные порядка 1000 шифрований, что требует порядка 100 миллисекунд. Дополнительное использование алгоритма перечисления ключей KEA позволяет сократить число измерений до 600.

Сейчас, изучив атаку в деталях, стоит ещё раз посмотреть на её план — теперь он будет гораздо понятнее.

Вместо заключения

На данный момент известно лишь об одной успешной атаке, проведенной данным способом. Эту атаку провели сами авторы оригинальной статьи. В качестве атакуемой видеокарты была выбрана Nvidia GeForce GT 620 с объемом видеопамяти 454MiB. Библиотека, реализующая шифрование — PolarSSL. Для детектирования электромагнитных следов авторами использовался осциллограф Agilent KeySight DSO9104A с пробником магнитного поля Rohde&Schwarz RF B.

Данная атака позволяет узнать значение последнего раундового ключа. В случае шифрования AES-128 этого достаточно, чтобы восстановить исходное значение секретного ключа, однако версии AES-192 и AES-256 остаются устойчивыми к взлому данным образом. Например, знание последнего раундового ключа AES-256 лишь сужает область возможных значений исходного с 2256 до 2128, и дальнейший подбор остается вычислительно неосуществим.

Атака впервые применяет изучение ЭМ-утечек информации к взлому шифрования на GPGPU и во многом превосходит другие известные атаки по стороннему каналу. Так, например, она требует на три порядка меньше измерений, чем атака, описанная в похожей работе.

Несмотря на то, что проведение атаки в реальной жизни на данный момент затруднительно, она остается интересной с научной точки зрения и может дать толчок дальнейшему развитию идей в исследуемом направлении.

P.S. На данный момент отличия в форматировании формул в редакторе и при просмотре поста несколько удивиляют, в ближайшее время постараюсь с этим разобраться.