3D ML. Часть 2: функции потерь в задачах 3D ML02.06.2020 17:17

Основной сложностью при выборе функций ошибок для работы с 3D данными является неевклидовость рассматриваемых структур, из-за которой задача определения расстояния в пространстве 3D моделей становится совсем нетривиальной.

В этой заметке мы поговорим о том, какие функции ошибки (Loss functions) алгоритмов используются в 3D ML, какие из них можно использовать в качеств метрик качества (metrics), а какие — в качестве регуляризаторов (regularizers).

Про то, чем евклидовы данные отличаются от неевклидовых, можно узнать здесь.

Серия 3D ML на Хабре:

Формы представления 3D данных
Функции потерь в 3D ML

Заметка от партнера IT-центра МАИ и организатора магистерской программы «VR/AR & AI» — компании PHYGITALISM.

В предыдущей части, мы обозначили, что работа с 3D структурами с привлечением методов машинного обучения приводит нас к новой обширной науке 3D ML. Среди всех задач этой области можно выделить класс подзадач, который мы назовём 2D-to-3D (также эта задача часто в англоязычной литературе имеет название »3D reconstruction from 2D image»). Эти задачи характеризуются тем, что на входе у алгоритма как правило одно или несколько изображений, а на выходе мы хотим получить какую-либо трехмерную структуру.

Например, можно восстанавливать карту глубины для произвольного изображения [2] (RGB-to-RGBD, или же можно было бы назвать такую задачу 2D-to-2.5D).

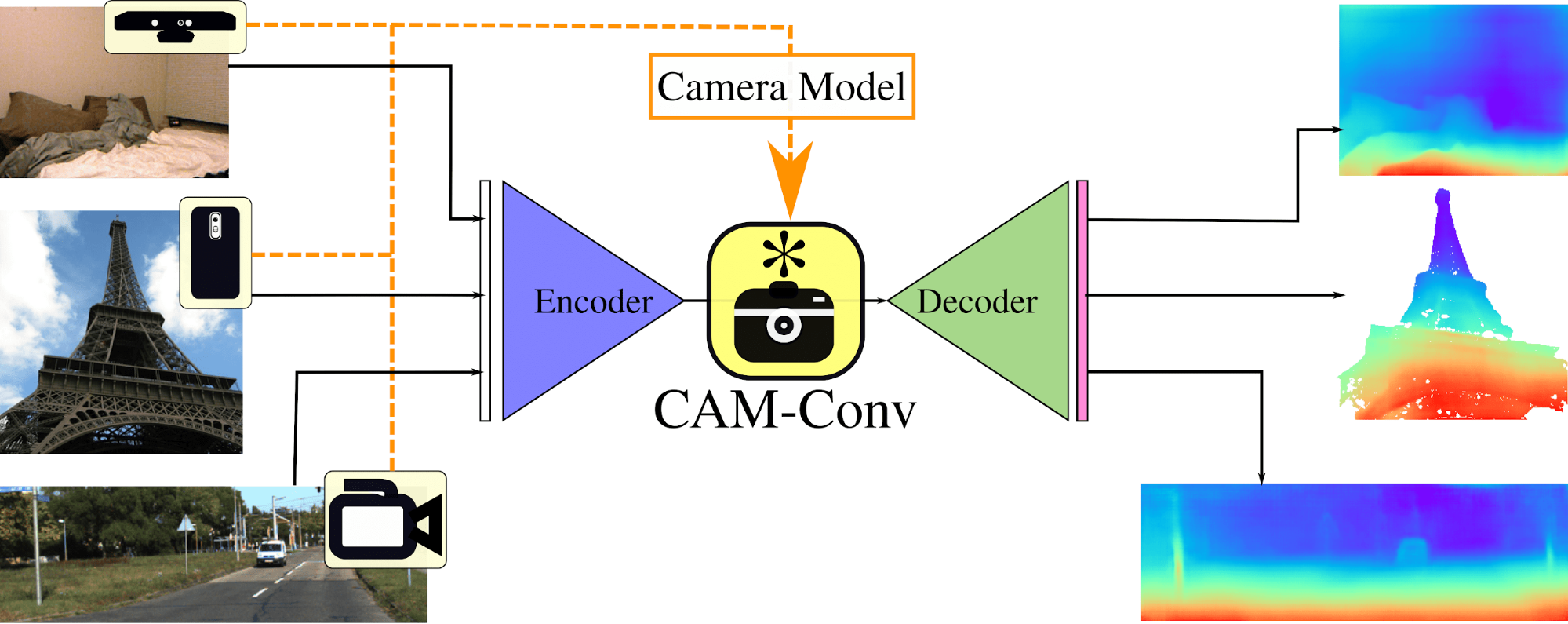
Рис. 1 Архитектура автокодировщика, восстанавливающая depth слой изображения при помощи специализированных сверточных операторов [3].

Другой пример схожего класса задач — восстановление облака точек объекта по его единственному RGB-D изображению [3] (2.5D-to-3D или »3D Shape completion»).

Рис. 2 Архитектура Voxlets [3] восстанавливает пространственную информацию для одного RGBD изображения: a — исходное RGB изображение;
b — воксельная модель, полученная с помощью depth слоя исходного снимка;
c — настоящая пространственная модель объектов; d — пространственная модель, полученная с помощью Voxlets.

В дальнейшем мы подробнее рассмотрим задачу 3D model reconstruction from single RGB image.

Рис. 3 Пример подготовленного входного изображения (слева) и полигональной модели, полученной с помощью Occupancy Net [1] (справа).

Поскольку результатом работы описанных выше алгоритмов являются трехмерные структуры, нам бы хотелось в первую очередь научится понимать, насколько результирующая модель близка к исходной модели из обучающей выборки.

Решение задачи машинного обучения, какая бы она не была (классификация, кластеризация, порождения новых объектов и т.д.) — это зачастую решение оптимизационной задачи. Для фиксированной параметризованной архитектуры алгоритма машинного обучения необходимо найти множество параметров, при которых функция ошибки (при выборе которой во многом отталкиваются от типа конкретной задачи) принимает наименьшее значение. При этом, необходимо следить, чтобы в процессе поиска минимума, обобщающая способность алгоритма возрастала. Подробнее про постановку задач машинного обучения и про классификацию задач можно прочесть здесь.

Оптимизируемые функции в задачах машинного обучения делятся на три категории:

Функции потерь (Loss functions/objectives) — позволяют вычислить ошибку алгоритма на каждом конкретном объекте. Выбираются обычно непрерывными и почти всюду дифференцируемыми для того чтобы применять градиентные методы. Среднее значение функции потерь на датасете (функционал качества алгоритма) оптимизируется в процессе обучения.

Регуляризаторы (Regularizers) — вводятся в функционал качества для того чтобы сделать оптимизационную задачу обучения корректной, процесс обучения устойчивым и получить более качественное решение. Зачастую регуляризация помогает избежать переобучения. В отличие от функции потерь, для вычисления значения регуляризатора зачастую не требуется использование информации об объектах из датасета.
Метрики качества (Metrics) — функции по которым определяется (валидируется) качество обученной модели (как на всем датасете в целом, так и на отдельных моделях), но не происходит непосредственной оптимизации. Используются для контроля переобучения и для сравнения различных моделей.

Далее мы подробнее поговорим про конкретные функции потерь и регуляризаторы, а для большей наглядности будем рассматривать примеры с кодом. Код с примерами к заметке доступен в нашем GitHub репозитории.

Как и в предыдущей части, в качестве тестовых моделей будем рассматривать модель икосферы и кролика, а в качестве рабочего инструмента будем использовать библиотеку pytorch3d.

Загрузка моделей и установка рабочего устройства

import os
import pathlib
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline

# You should work in Jupyter.
from tqdm import tqdm_notebook

from celluloid import Camera

import torch

# untilitis 
from pytorch3d.utils import ico_sphere

# loss functions and regulaziers
from pytorch3d.loss import (
    chamfer_distance,
    mesh_edge_loss,
    mesh_laplacian_smoothing,
    mesh_normal_consistency
)

# io utils
from pytorch3d.io import load_obj

# operations with data
from pytorch3d.ops import sample_points_from_meshes

# datastructures
from pytorch3d.structures import Meshes, Textures

# render 
from pytorch3d.renderer import (
    look_at_view_transform,
    OpenGLPerspectiveCameras,
    DirectionalLights, 
    RasterizationSettings, 
    MeshRenderer, 
    MeshRasterizer,  
    HardPhongShader
)

import trimesh
from trimesh import registration
from trimesh import visual

# If you have got a CUDA device, you can use GPU mode
if torch.cuda.is_available():
  device = torch.device('cuda:0')
  torch.cuda.set_device(device)
else:
  device = torch.device('cpu')

Подготовка моделей

# Bunny mesh in pytorch3d
verts, faces_idx, _ = load_obj(path_to_model)
faces = faces_idx.verts_idx

center = verts.mean(0)
verts = verts - center
scale = max(verts.abs().max(0)[0])
verts = verts / scale

# Initialize each vertex to be white in color.
verts_rgb = torch.ones_like(verts)[None]  # (1, V, 3)

textures = Textures(verts_rgb=verts_rgb.to(device))

# Create a Meshes object for the bunny.
bunny_mesh = Meshes(
    verts=[verts.to(device)],   
    faces=[faces.to(device)], 
    textures=textures
)

# Sphere mesh in pytorch3d
sphere_mesh = ico_sphere(4, device)
verts_rgb = torch.ones_like(sphere_mesh.verts_list()[0])[None]
sphere_mesh.textures = Textures(verts_rgb=verts_rgb.to(device))

# Mesh to pointcloud with normals in pytorch3d
num_points_to_sample = 25000

bunny_vert, bunny_norm = sample_points_from_meshes(
    bunny_mesh,
    num_points_to_sample ,
    return_normals=True
)

sphere_vert, sphere_norm = sample_points_from_meshes(
    sphere_mesh,
    num_points_to_sample,
    return_normals=True
)

def convert_to_mesh(mesh):
    """Trimesh может загружать сцены вместо монолитного объекта
    """
    if isinstance(mesh, trimesh.Scene):
        return mesh.dump(concatenate=True)
    else:
        return mesh

def scale_to_unit(mesh: trimesh.Trimesh):
    length, weight, height = mesh.extents
    scale = 1 / max(length, weight, height)
    mesh.apply_scale((scale, scale, scale))

mesh_target = convert_to_mesh(trimesh.load_mesh(str(path_to_orig)))
mesh_source = convert_to_mesh(trimesh.load_mesh(str(path_to_rot)))

mesh_target.rezero()
mesh_source.rezero()
scale_to_unit(mesh_target)
scale_to_unit(mesh_source)

mesh_source.visual = visual.ColorVisuals(mesh_source, vertex_colors=(255, 0, 0, 255))
mesh_target.visual = visual.ColorVisuals(mesh_target, vertex_colors=(0, 255, 0, 255))

scene = trimesh.Scene([mesh_source, mesh_target])

Подготовка визуализации моделей

# Initialize an OpenGL perspective camera.
cameras = OpenGLPerspectiveCameras(device=device)

# We will also create a phong renderer. This is simpler and only needs to render one face per pixel.
raster_settings = RasterizationSettings(
    image_size=1024, 
    blur_radius=0, 
    faces_per_pixel=1, 
)

# We can add a directional light in the scene. 
ambient_color = torch.FloatTensor([[0.0, 0.0, 0.0]]).to(device)
diffuse_color = torch.FloatTensor([[1.0, 1.0, 1.0]]).to(device)
specular_color = torch.FloatTensor([[0.1, 0.1, 0.1]]).to(device)
direction = torch.FloatTensor([[1, 1, 1]]).to(device)
lights = DirectionalLights(ambient_color=ambient_color,
                           diffuse_color=diffuse_color,
                           specular_color=specular_color,
                           direction=direction,
                           device=device)

phong_renderer = MeshRenderer(
    rasterizer=MeshRasterizer(
        cameras=cameras, 
        raster_settings=raster_settings
    ),
    shader=HardPhongShader(
        device=device, 
        cameras=cameras, 
        lights=lights
        )
)

# Select the viewpoint using spherical angles  
distance = 2.0   # distance from camera to the object`
elevation = 40.0   # angle of elevation in degrees
azimuth = 0.0  # No rotation so the camera is positioned on the +Z axis. 

# Get the position of the camera based on the spherical angles
R, T = look_at_view_transform(distance, elevation, azimuth, device=device,at=((-0.02,0.1,0.0),))

# Render the bunny providing the values of R and T. 
image_bunny = phong_renderer(meshes_world=bunny_mesh, R=R, T=T)
image_sphere = phong_renderer(meshes_world=sphere_mesh, R=R, T=T)

image_sphere = image_sphere.cpu().numpy()
image_bunny = image_bunny.cpu().numpy()

Визуализация моделей

# Source mesh of sphere
plt.figure(figsize=(13, 13))
plt.imshow(image_sphere.squeeze())
plt.grid(False)

# Target mesh of bunny
plt.figure(figsize=(13, 13))
plt.imshow(image_bunny.squeeze())
plt.grid(False)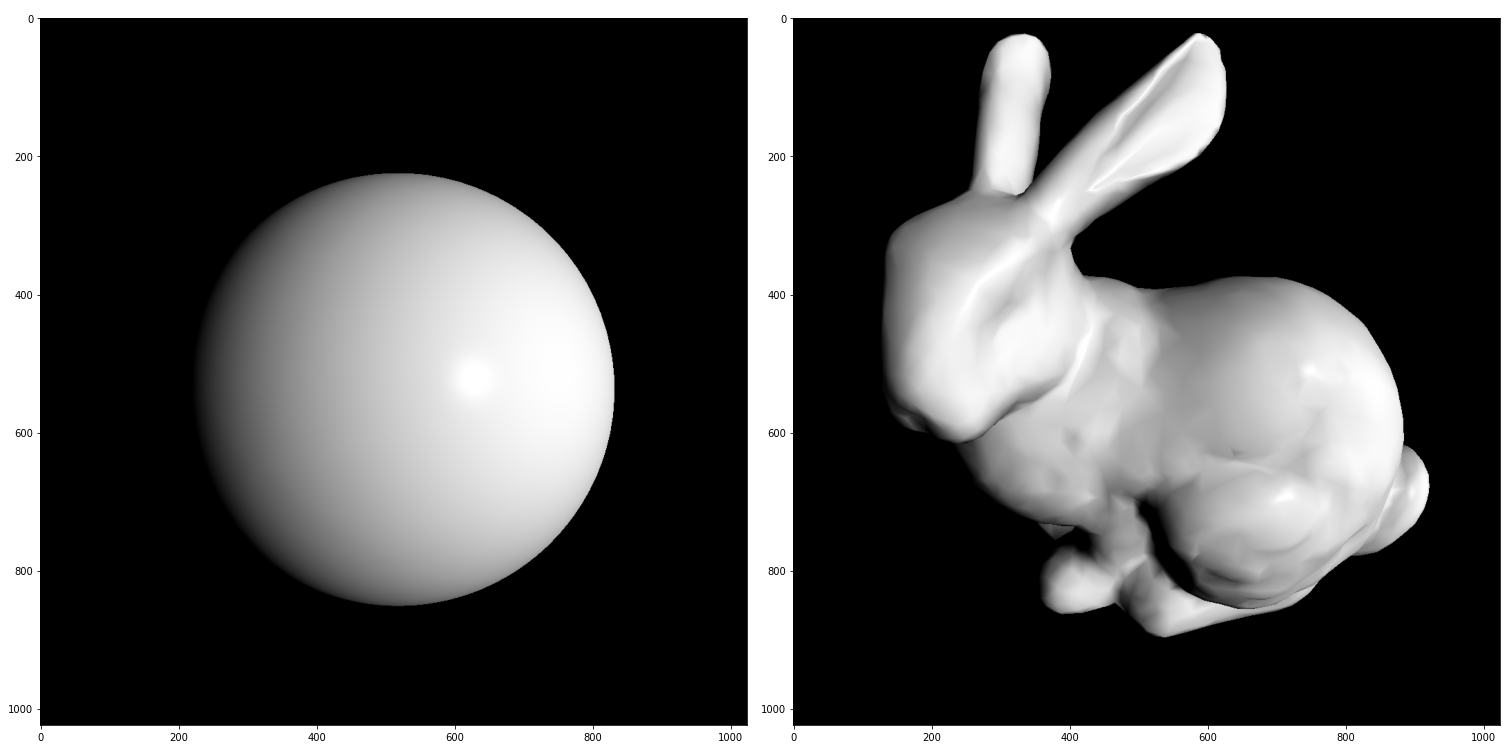

Прежде чем ввести в рассмотрение конкретные функции потерь, отметим, что две сравниваемые модели должны быть предварительно приведены к одинаковому масштабу и ориентированы друг относительно друга таким образом, чтобы функция потерь принимала свое наименьшее значение из всех возможных при различных взаимных ориентациях. Решением задачи по совмещению друг с другом двух трехмерных объектов занимаются алгоритмы регистрации облаков точек, реализации которых можно найти в библиотеках trimesh или pcl.

В качестве примера задачи регистрации рассмотрим совмещение двух полигональных моделей автомобилей (mesh_source.obj и mesh_target.obj из директории data).

scene.show()

В качестве метода регистрации можно взять метод главных осей инерции (principal axes of inertia) — разновидности метода ICP.

transform, cost = registration.mesh_other(mesh_source, mesh_target, samples=2_000, scale=True)
new_scene = scene.copy()
new_scene.geometry["geometry_0"].apply_transform(transform)

print("Величина ошибки регистрации: ", cost)
print("Матрица преобразования модели:")
print(transform)

Out:

>>Величина ошибки регистрации:  2.5801412889832494e-10
>>Матрица преобразования модели:
>>[[-0.97327281  0.33386218 -0.23301026  0.65454393]
 [-0.07505283  0.44631862  0.95298713 -0.01844067]
 [ 0.40015598  0.89574184 -0.38799414  0.28013195]
 [ 0.          0.          0.          1.        ]]

После применения алгоритма можно увидеть, что модели совместились:

new_scene.show()

Помимо рассмотренного метода регистрации в библиотеке trimesh также содержится классический алгоритм icp и метод Procrustes analysis. Пример применения другого метода к данным моделям можно найти в jupyter notebook 3dml_habr_phygitalism_part_2.ipynb.

Заметим, что для практических приложений скорость работы рассматриваемых алгоритмов может быть недостаточно, в силу того, что их реализации написана на языке Python. В случае, если есть необходимость в имплементации более быстрых версий алгоритмов регистрации или иных алгоритмов из trimesh, можно воспользоваться библиотекой trimesh2, написанной на языке C++.

1. IoU metric

Метрика Intersection over Union ( $IoU$ ), также известная как Jaccard index, — число от 0 до 1, показывающее, насколько у двух объектов (эталонного (ground true) и текущего) совпадает внутренний «объем».

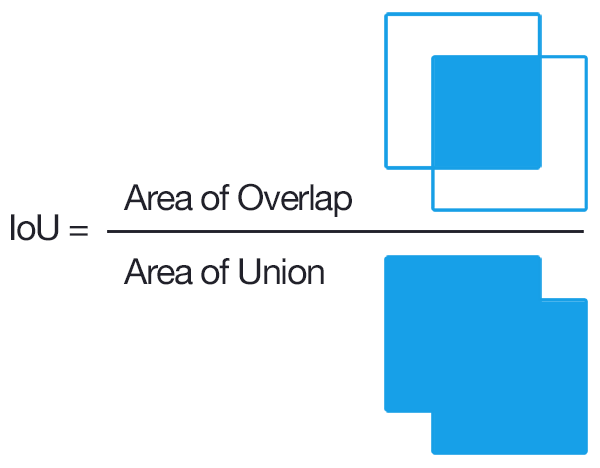
Формально, для двух непустых множеств A и B, функция IoU определяется как:

$IoU(A,B) = \frac{|A \cap B|}{|A \cup B|}.$

Для того чтобы подсчитать $IoU$ необходимо уметь вычислять внутренний объем рассматриваемых объектов. В случаи с полигональными моделями чаще всего прибегают к оценке объема методом Монте-Карло.

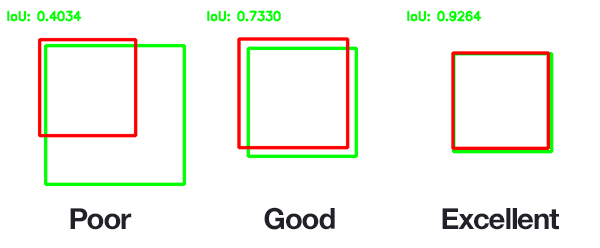
В задачах компьютерного зрения и 3D ML $IoU$ часто используют при оценке того, насколько корректно найден ограничивающий прямоугольник или ограничивающий параллелепипед (bounding box), т.е. в качестве метрики качества алгоритма, но в последнее время появились различные модификации $IoU$ , которые могут использованы и в качестве функции потерь [9].

В случае с трехмерными объектами $IoU$ обычно используется в качестве метрики, однако данная метрика не всегда корректна. Действительно, большая часть информации об объекте определяется его поверхностью. На рисунке ниже продемонстрировано, что две модели могут иметь существенно отличные поверхности, при этом значение $IoU$ будет высоко.

Для воксельных моделей значение данной метрики может быть некорректным ещё и по той причине, что «внутренность» моделей может отличаться, даже если у них схожие поверхности. На изображении ниже, из статьи [1], авторы продемонстрировали то, как при увеличении разрешения воксельной сетки растет качество $IoU$ метрики, но в тоже время растет и количество затрачиваемой памяти, времени обучения и параметров воксельной архитектуры. Для функциональной же модели (в данном случае Occupancy Net) качество не зависит от разрешения, а количество параметров неизменно.

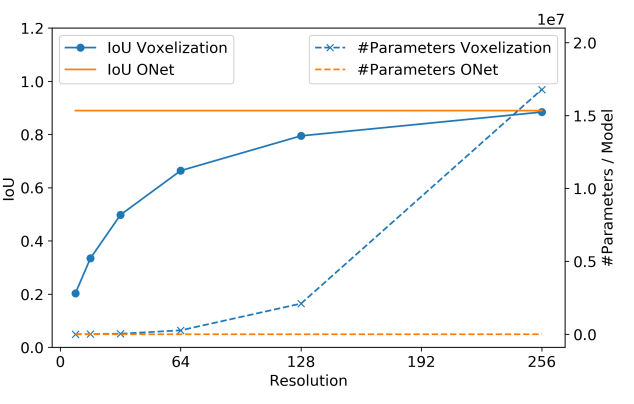
Для работы с облаками точек данная функция обычно не применяется из-за того, что определить понятие объёма пересечения облаков точек достаточно затруднительно, однако такая возможность все равно имеется, так например в [8] авторы преобразуют выходное облако точек для их архитектуры в воксельную модель и сравнивают качество работы полученной модели по $IoU$ метрике. Для оценки качества работы модели на всем датасете обычно подсчитывают средние значения данной функции — $mIoU$ (mean intersection over union) для всего датасета и для отдельных категорий. Метрика $IoU$ в процессе обучения максимизируется.

2. Chamfer loss/distance

Данная функция используется для работы как с полигональными моделями, так и с облаками точек. Она показывает, насколько вершины одной полигональной модели (облака точек) близки к вершинам другой полигональной модели (облаку точек), и следовательно, подлежит минимизации. Обычно сравнивают полигональную модель, полученную в результате работы алгоритма, и аналогичную модель из датасета.

Пусть мы имеем два множества вершин (точек) в трехмерном пространстве $P$ и $Q$ . Введем в рассмотрение множество пар $(p,q)$ , такое, что для $\forall p \in P$ точка $q \in Q$ будет ближайшим соседом, т.е.:

$\Lambda_{P,Q} = \{ (p, \arg \min_{q \in Q}\|p-q \|)\colon p \in P \},$

тогда chamfer loss для данных точечных множеств определяется как:

$\mathcal{L}_{cham}(P,Q) = |P|^{-1} \: \sum_{(p,q) \in \Lambda_{P,Q}}\|p-q\|^2 \: + \: \sum_{(q,p) \in \Lambda_{Q,P}}\|q-p\|^2$

Зачастую для вычисления chamfer loss имеющихся вершин полигональной модели недостаточно, поэтому дополнительно сэмплируют точки на гранях моделей, например так, как это делают авторы в недавно вышедшей работе [5]. Chamfer loss используется в качестве функции потерь. В [17] предложена модификация chamfer loss, использующая семплирования дополнительных точек на полигонах для вычисления значения функции потерь.

3. Normal loss / distance

Пусть аналогично предыдущему пункту мы рассматриваем два точечных множества $P$ и $Q$ , но помимо информации о вершинах мы можем также использовать информацию о нормалях, в частности, можем восстанавливать единичную нормаль $u$ к произвольной точке $p$ — $u_p$ , тогда normal loss для данных точечных множеств определяется как:

$\mathcal{L}_{norm}(P,Q) = -|P|^{-1}\negthickspace \sum_{(p,q) \in \Lambda_{P,Q}}|u_q \cdot u_p| \: - \: |Q|^{-1}\negthickspace \sum_{(q,p) \in \Lambda_{Q,P}}|u_p \cdot u_q|$

Normal loss используется в качестве функции потерь и показывает, насколько сильно различаются поля нормалей у двух полигональных моделей, т.е. по сути, минимизируя данный критерий, мы стараемся сделать углы между соответствующими нормалями как можно меньше.

Вычислим значение chamfer loss и normal loss для наших тестовых моделей:

# Chamfer loss and normal loss
loss_chamfer, loss_normals_chamfer = chamfer_distance(
    bunny_vert, 
    sphere_vert, 
    x_normals=bunny_norm,
    y_normals=sphere_norm
)

print("Chamfer loss =", loss_chamfer.item())
print("Normal loss =", loss_normals_chamfer.item())

Out:

>>Chamfer loss = 0.2609584927558899
>>Normal loss = 0.47336119413375854

4. Edge loss / regularizer

Недостатком chamfer и normal loss является чувствительность к выбросам. На рисунки ниже продемонстрирована ситуация, когда значение chamfer distance (CD) для двух в равной степени непохожих на оригинал объектов может значительно отличаться.

Помимо чувствительности к выбросам, на практике часто наблюдается эффект перекрытия полигонов. Чтобы избежать появления данного эффекта, вместе с chamfer и normal loss используют специальные регуляризаторы формы итогового меша (shape regularizers). Пусть $V$ — множество вершин полигональной модели, а $E$ — множество ребер модели, тогда в качестве регуляризатора формы меша можно использовать среднее значение длины ребер:

$\mathcal{L}_{edge}(V,E) = \frac{1}{|E|}\sum_{(v,v') \in E}\|v-v'\|^2, \: E \subseteq V \times V.$

Авторы в [5], используя данный регуляризатор, улучшили качество итоговых моделей, что можно увидеть на изображениях ниже. Edge normalizer вводится дополнительным слагаемым к основной функции потерь с положительным коэффициентом.

Рис. 4 Пример из статьи [5]: восстановление меша из изображения без использования регуляризатора формы (лучший результат) и с использованием регуляризатора формы (средний результат).

Рис. 5 Пример из статьи [5]: сравнение результатов восстановления меша сетью, использовавшей регуляризатор при обучении (Mesh R-CNN), с сетью, в которой регуляризатор не использовался (Pixel2Mesh+).

Сравним значение данного регуляризатора для наших моделей:

print("Edge loss for bunny.obj:", mesh_edge_loss(bunny_mesh).item())
print("Edge loss for sphere.obj:", mesh_edge_loss(sphere_mesh).item())

Out:

>>Edge loss for bunny.obj: 0.004127349238842726
>>Edge loss for sphere.obj: 0.005724199116230011

5. Smooth loss / regularizer

Для того, чтобы итоговые модели имели более гладкие поверхности без выбросов и шума, часто прибегают к сглаживающим регуляризаторам. Простейшим сглаживающим регуляризатором является Smooth loss. Для его вычисления необходимо провести суммирование по всем «внутренним» двугранным углам между полигонами меша $x$ :

$\mathcal{L}_{sm}(x) = \sum_{\theta_i \in \mathcal{E}} (\cos \theta_i + 1)^2.$

Введенная таким образом функция регуляризатора как бы стремится «распрямить» меш так, чтобы минимизировать поверхностное натяжение.

Рис. 6 Пример из статьи [10]: сравнение работы алгоритма 2D-to-3D без использования smooth regularizer и с использованием данного регуляризатора. Слева направо: входное изображение, восстановленная полигональная модель без использования smooth regularizer, восстановленная полигональная модель c использования smooth regularizer.

Сравним значение данного регуляризатора для наших моделей:

print("Smooth regularizer for bunny.obj:", mesh_normal_consistency(bunny_mesh).item())
print("Smooth regularizer for sphere.obj:", mesh_normal_consistency(sphere_mesh).item())

Out:

>>Smooth regularizer for bunny.obj: 0.03854169696569443
>>Smooth regularizer for sphere.obj: 0.0009780693799257278

6. Hausdorff losses

Проблема определения функции расстояния между двумя поверхностями в пространстве (которая используется для построения функции ошибки) стояла задолго до появления компьютерной графики. Вопрос о том, как находить расстояние между двумя вложенными в некоторое пространство многообразиями, был поставлен в функциональном анализе, и сегодня многие исследователи, при определении функции ошибки в задачах 3D ML, пользуются результатами из этой области. Так, в частности, существуют подходы, основанные на понятии метрики Хаусдорфа. Рассмотрим два таких подхода.

Оба подхода базируются на одинаковых математических понятиях, поэтому сначала опишем их. Во-первых, будем считать, что расстояние между некоторой точкой пространства $p$ и поверхностью $S'$ в этом пространстве определяется с помощью Евклидовой нормы следующим образом:

$d\left(p, \mathcal{S}^{\prime}\right)=\min _{p^{\prime} \in \mathcal{S}^{\prime}}\left\|p-p^{\prime}\right\|_{2},$

тогда «одностороннее» расстояние между двумя поверхностями $S$ и $S^\prime$ можно определить как:

$d\left(\mathcal{S}, \mathcal{S}^{\prime}\right)=\max _{p \in \mathcal{S}} d\left(p, \mathcal{S}^{\prime}\right).$

Под «односторонностью» здесь имеется в виду несимметричность данной функции. Чтобы определить симметричную функцию расстояния между двумя множествами, Хаусдорф предложил следующую конструкцию (называемую сегодня метрикой Хаусдорфа):

$d_{s}\left(\mathcal{S}, \mathcal{S}^{\prime}\right)=\max \left[d\left(\mathcal{S}, \mathcal{S}^{\prime}\right), d\left(\mathcal{S}^{\prime}, \mathcal{S}\right)\right].$

В качестве функции потерь, впрочем, используют не саму метрику, а средние значения расстояний от точки до поверхности. Введем в рассмотрении две функции. Средняя ошибка (mean distance error) между двумя поверхностями определяется как:

$d_{m}\left(\mathcal{S}, \mathcal{S}^{\prime}\right)=\frac{1}{|\mathcal{S}|} \iint_{p \in \mathcal{S}} d\left(p, \mathcal{S}^{\prime}\right) d S ,$

где $|S|$ — означает площадь поверхности $S$ , а среднеквадратичная ошибка (root mean square distance error) между двумя поверхностями определяется как:

$d_{r m s e}\left(\mathcal{S}, \mathcal{S}^{\prime}\right)=\sqrt{\frac{1}{|\mathcal{S}|} \iint_{p \in \mathcal{S}} d\left(p, \mathcal{S}^{\prime}\right)^{2} d S}.$

Существуют различные подходы к тому, как вычислять средние ошибки по Хаусдорфу на полигональном меше. Так, например, в [13] предложено вычислять значения средней ошибки на основании подсчета «ориентированных расстояний» между точкой и поверхностью. Такой подход авторы назвали Metro distance.

Рис. 7 Пример из статьи [13]: сравнение двух мешей одного объекта: высокополигональная исходная модель (слева), оптимизированная низкополигональная модель.

В статье [14] авторы предлагают вычислять среднеквадратичную ошибку и конструируют оптимизированный численный метод для интегрирования по поверхности меша. Такой подход авторы называют Mesh distance.

Рис. 8 Пример из статьи [13]: средняя ошибка, вычисленная по расстоянию Metro, для низкополигональной модели по сравнению с исходной высокополигональной моделью.

Также в статье [14] приведено сравнение этих двух подходов: Mesh distance оказывается более быстрым и экономным с точки зрения затраченной памяти способом вычисления Хаусдорфова расстояния. Данные функции можно использовать в качестве регуляризатора, если на каждой итерации алгоритма обучения хранить меш объекта с предыдущей итерации, и высчитывать значение ошибки приближения текущего меша предыдущим.

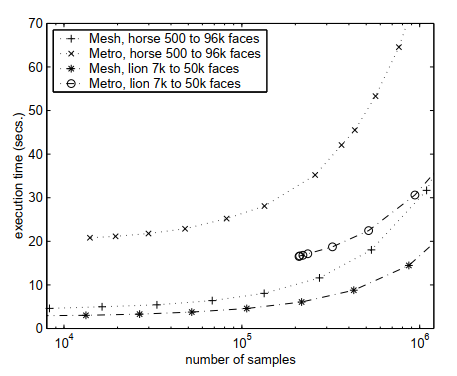
Рис. 9 Пример из статьи [14]: сравнение вычислительной эффективности Mesh distance и Metro distance.

7. Laplacian loss / regularizer

Еще одним примером сглаживающего регуляризатора является Laplacian loss. Для того, чтобы сконструировать этот регуляризатор, используют часто возникающий в 3D ML и в компьютерной графике т.н. umbrella operator [15] — дискретизацию оператора Лапласа, вычисленного в вершинах полигонального меша:

$\mathcal{U}(\mathbf{p})=\frac{1}{n} \sum_{i=0}^{n-1} \mathbf{p}_{i}-\mathbf{p}$

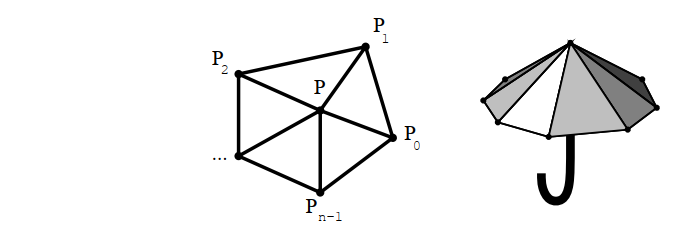
Суммирование производится по вершинам, которые связаны с данной вершиной. В дальнейшем будем использовать обозначение $\mathcal{N}(p)$ для множества вершин, которые связаны с данным ребром. Можно рассматривать применение данного оператора как перевод вершин в новую систему координат. Такие координаты называют Лапласовыми. В [12] и [16] идея использования данного оператора применяется к задачам сглаживания, деформирования и конкатенации меша.

Рис. 10 Пример из статьи [12]: сглаживание меша с помощью применения Laplacian smooth. (а) — исходный меш, (b) — после многократного применения Laplacian smooth.

Если оператор преобразования вершины меша в Лапласовы координаты будет иметь вид:

$\delta_{p}=p-\sum_{k \in \mathcal{N}(p)} \frac{1}{\left\|\mathcal{N}{(p)}\right\|} k,$

тогда Лапласов регуляризатор определяется как:

$\mathcal{L}_{Lap}(x)=\sum_{p}\left\|\delta_{p}^{\prime}-\delta_{p}\right\|_{2}^{2}$

где суммирование производится по всем вершинам меша, а штриховая Лапласова координата обозначает меш на предыдущей итерации. Применительно к решению задачи 2D-to-3D данный регуляризатор применяется, например, в [11].

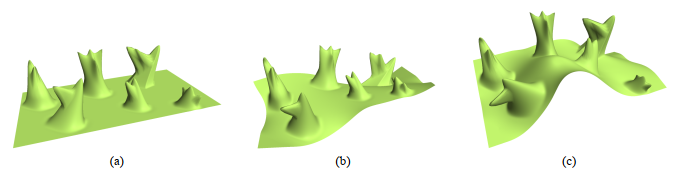
Рис. 11 Пример из статьи [16]: деформирование меша с помощью применения Laplacian smooth.

Рис. 12 Пример из статьи [16]: конкатенация меша с помощью применения Laplacian smooth. (а), (b) — исходные меши, © — конкатенированный меш, полученный с помощью применения Laplacian smooth.

Сравним значение данного регуляризатора для наших моделей:

print("Laplacian smoothing objective for bunny.obj:", mesh_laplacian_smoothing(bunny_mesh).item())
print("Laplacian smoothing objective for sphere.obj:", mesh_laplacian_smoothing(sphere_mesh).item())

Out:

>>Laplacian smoothing objective for bunny.obj: 0.014459558762609959
>>Laplacian smoothing objective for sphere.obj: 0.0040009506046772

Хорошую видеолекцию на тему применения оператора Лапласа в компьютерной графике можно найти здесь.

8. F1 score

Если считать, что количество вершин в восстановленном меше (retrieval) равно количеству вершин в целевом меше (ground true), то каждую вершину восстановленного меша можно отнести либо к правильно восстановленой, либо к неправильно восстановленной. Для этого вводится пороговое значение расстояния между вершинами восстановленного и исходного объектов: если расстояние между соответствующими вершинами меньше порогового, то данную вершину восстановленного меша относят к верно восстановленной. Таким образом, для каждой вершины восстановленного меша можно определить два класса и использовать для всего объекта метрики качества задач классификации. В частности, как это продемонстрировано в работах [5,6], можно использовать F1 метрику, являющуюся средним гармоническим между точностью (precision) и полнотой (recall). Точность в данном случае определяется как отношение количества вершин восстановленного меша, находящихся в пределах порогового расстояния от соответствующих вершин исходного меша. Полнота определяется симметрично, как отношение количества точек исходного меша, лежащих не более чем на пороговом расстоянии от соответствующих точек восстановленного меша.

F1 устойчива к выбросам и лучше отражает качество восстановления формы объекта. F1 метрика максимизируется. Реализацию данной метрики и некоторых других можно найти в библиотеке pytorch geometric — фреймворке для работы с пространственными графами.

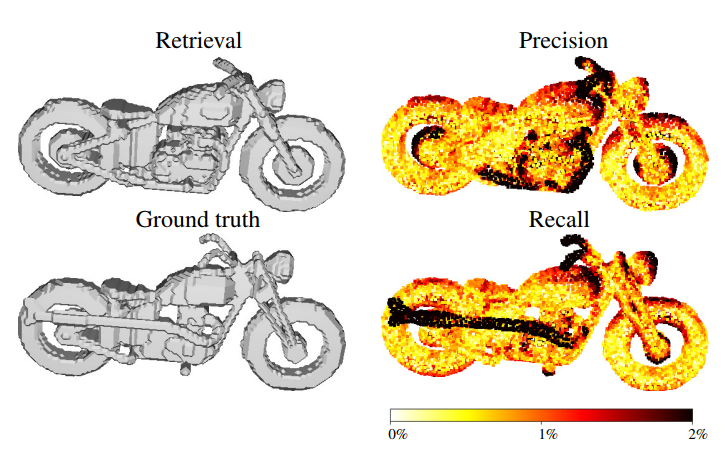
Рис. 13 Пример из статьи [6]: слева сверху — восстановленный меш, слева снизу — исходный меш, справа сверху для восстановленного меша показано, насколько его вершины отличаются от исходного (в % длины ограничивающего параллелепипеда (bounding box)), справа снизу — для исходного меша показано, насколько его вершины отличаются от восстановленного (в % длины ограничивающего параллелепипеда (bounding box)).

9. Earth mover«s distance

Еще одной часто применяемой метрикой, в основном для облаков точек, является Earth mover«s distance (EMD), также известной в более общем виде как Wasserstein metric. Данная метрика возникает в задачах кластеризации изображений. До наступления эпохи глубокого обучения эта метрика часто применялась в области анализа изображений. Вычисление метрики тесно связано с решением оптимизационной транспортной задачи (подробнее про это и про то, как использовать эту метрику для различных типов данных, можно прочитать здесь).

Формально EMD определяется как минимальное значение функционала расстояния в следующей вариационной задаче:

$d_{E M D}\left(S_{1}, S_{2}\right)=\min _{\phi: S_{1} \rightarrow S_{2}} \sum_{x \in S_{1}}\|x-\phi(x)\|_{2},$

$S_{1}, S_{2} \subseteq \mathbb{R}^{3}, \quad s=\left|S_{1}\right|=\left|S_{2}\right|,$

$\phi: S_{1} \rightarrow S_{2}.$

Самое оптимальное биективное отображение в каждой конкретной задаче отличается, но преимуществом данной метрики является то, что оно инвариантно к произвольным инфиниматезиальным преобразованиям облака точек. Честное решение данной оптимизационной задачи обычно очень вычислительно затратно в задачах глубокого обучения, даже при использовании видеокарт, поэтому часто используют аппроксимированное вычисление этой метрики [7], как например это сделали авторы в [8]. Критерий EMD минимизируется в процессе обучения.

Рис. 14 Пример из статьи [8]: сравнение восстановления средней формы (в смысле распределения исходных облаков точек) с помощью расстояний chamfer distance (CD) и Earth mover«s distance (EMD) для различных синтетических двумерных облаков точек (a-d).

Чтобы лучше понять, как изменяются рассмотренные выше функции потерь и регуляризаторы в процессе обучения, рассмотрим модельный пример. Предположим, что модель сферы это исходное приближение, которое может генерировать наша модель машинного обучения, а в качестве целевой модели выступает модель кролика.

В качестве параметров модели машинного обучения возьмем координаты генерируемого меша (в данном случае сферы) и зададим оптимизатор, который будет минимизировать рассогласование между source (sphere) и target (bunny):

deform_verts = torch.full(sphere_mesh.verts_packed().shape, 0.0, device=device, requires_grad=True)
optimizer = torch.optim.SGD([deform_verts], lr=1.0, momentum=0.9)

Зафиксируем параметры оптимизационного процесса:

# Number of optimization steps
Niter = 3000
# Weight for the chamfer loss
w_chamfer = 1.0 
# Weight for mesh edge loss
w_edge = 1.0 
# Weight for mesh normal consistency
w_normal = 0.01 
# Weight for mesh laplacian smoothing
w_laplacian = 0.1 
# Plot period for the losses
plot_period = 50

chamfer_losses = []
laplacian_losses = []
edge_losses = []
normal_losses = []

В цикле будем делать градиентный спуск по функции потерь, представляющей из себя взвешенную сумму функций ошибок и регуляризаторов:

$\mathcal{L} = \omega_c \mathcal{L}_{cham} + \omega_n \mathcal{L}_{norm} + \omega_e \mathcal{L}_{edge} + \omega_l \mathcal{L}_{Lap}$

loop = tqdm_notebook(range(Niter))

fig = plt.figure()
camera = Camera(fig)

for i in loop:
    # Initialize optimizer
    optimizer.zero_grad()

    # Deform the mesh
    new_src_mesh = sphere_mesh.offset_verts(deform_verts)

    # We sample 5k points from the surface of each mesh 
    sample_trg = sample_points_from_meshes(bunny_mesh, 5000)
    sample_src = sample_points_from_meshes(new_src_mesh, 5000)

    # We compare the two sets of pointclouds by computing (a) the chamfer loss
    loss_chamfer, _ = chamfer_distance(sample_trg, sample_src)

    # and (b) the edge length of the predicted mesh
    loss_edge = mesh_edge_loss(new_src_mesh)

    # mesh normal consistency
    loss_normal = mesh_normal_consistency(new_src_mesh)

    # mesh laplacian smoothing
    loss_laplacian = mesh_laplacian_smoothing(new_src_mesh, method="uniform")

    # Weighted sum of the losses
    loss = loss_chamfer * w_chamfer + loss_edge * w_edge + loss_normal * w_normal + loss_laplacian * w_laplacian

    # Print the losses
    loop.set_description('total_loss = %.6f' % loss)

    # Save the losses for plotting
    chamfer_losses.append(loss_chamfer)
    edge_losses.append(loss_edge)
    normal_losses.append(loss_normal)
    laplacian_losses.append(loss_laplacian)

    # Plot mesh
    if i % plot_period == 0 or i==0:

        # Render the bunny providing the values of R and T. 
        image_bunny = phong_renderer(meshes_world=new_src_mesh, R=R, T=T)
        image_bunny = image_bunny.detach().cpu().numpy()

        plt.imshow(image_bunny.squeeze())
        plt.grid(False)
        camera.snap()

    # Optimization step
    loss.backward()
    optimizer.step()

Для того, чтобы лучше понять динамику процесса оптимизации, мы использовали библиотеку celluloid для создании анимации.

Посмотрим, как изменялись функции потерь и регуляризаторы в процессе обучения:

# Losses evaluation
fig = plt.figure(figsize=(13, 5))
ax = fig.gca()
ax.plot(chamfer_losses, label="chamfer loss")
ax.plot(edge_losses, label="edge loss")
ax.plot(normal_losses, label="normal loss")
ax.plot(laplacian_losses, label="laplacian loss")
ax.legend(fontsize="16")
ax.set_xlabel("Iteration", fontsize="16")
ax.set_ylabel("Loss", fontsize="16")
ax.set_title("Loss vs iterations", fontsize="16")

Помимо перечисленных выше метрик используются и другие. Так, например, для воксельного представления моделей, воксели часто «вытягивают» в обычные числовые вектора и пользуются метриками и функциями потерь для векторов [4], например косинусной мерой.

После того, как модель обучена и показывает приемлемый результат по метрикам качества, ее нужно встраивать в общий pipeline обработки данных в конкретном проекте. На этом этапе появляются другие показатели качества используемой модели, такие как: размер памяти, которая занимает модель; размер памяти, необходимой для обработки данных моделью; скорость обработки данных моделью; время, необходимое для пере/дообучения модели. Все эти характеристики относят к внешним метрикам качества, в то время как рассмотренные выше метрики относят к внутренним метрикам качества решаемой задачи. Так же немаловажно, чтобы полученная архитектура и способ ее обучения были воспроизводимы. Обычно в статьях, описывающих новую архитектуру, указывается только алгоритм обучения, его параметры, и на каком датасете производилось обучение. Пример того, как измеряется производительность моделей глубокого обучения и некоторые связанные с этим аспекты, можно посмотр