10 занимательных задач
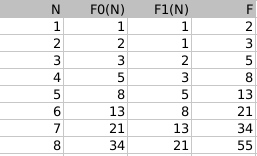
Обозначим F (N) число строк длины N, не содержащих две единицы подряд. Обозначим F0(N) число строк длины N, не содержащих две единицы подряд и заканчивающихся на 0. Обозначим F1(N) число строк длины N, не содержащих две единицы подряд и заканчивающихся на 1.Выведем рекуррентные формулы для F0 и F1.F1(N) = F0(N-1). Так как две единицы подряд идти не может, число строк, заканчивающихся на 1, равно числу строк на 1 меньшей длины, заканчивающихся на 0.F0(N) = F0(N-1) + F1(N-1). Ноль можно дописать к любой корректной строке, не нарушив при этом условия. Значит, число строк, заканчивающихся на 0, равно числу строк на 1 меньшей длины.
F0(N) = F0(N-1) + F1(N-1) = F0(N-1) + F0(N-2). Итак, F0 представляет собой ряд Фибоначчи с неким сдвигом. F1(N) = F0(N-1), значит F1 тоже состоит из чисел Фибоначчи, с «отставанием» на 1 относительно F0.
F (N) = F0(N) + F1(N). Член F (N) получается, когда число из ряда Фибоначчи F0 складывают с числом из ряда Фибоначчи F1, которое является для него предыдущим числом. А сумма числа Фибоначчи с предыдущим числом Фибоначчи — это тоже число Фибоначчи (по формуле чисел Фибоначчи). Итак, мы доказали, что число строк, не включающих две единицы подряд, будет является числом Фибоначчи. Осталось определить значение F (N) для первых двух N. F (1) = 2 (две подходящие последовательности:»0» и »1»), F (2) = 3 (три подходящие последовательности:»00»,»01»,»10»).