10 новых сказок о потерянном времени27.12.2016 10:33

Привет Хабр!

Я решил продолжить серию статей про гипотезу Эйлера, написав несколько улучшенных версий программ для решения диофантова уравнения вида a5 + b5 + c5 + d5 = e5.

22884af5edb445fdaef33cb76624628c.png

Как известно, для того, чтобы решить какую-либо сложную вычислительную задачу, нужно обратить внимание как минимум на следующие пункты:

  1. Эффективный алгоритм
  2. Быстрая реализация
  3. Мощное железо
  4. Распараллеливание

Я уделил больше всего внимания первому пункту. Давайте посмотрим, что из этого получилось.

Сразу отмечу, что код писался на С++, компилировался 32-битный MS Visual C++ 2008 Compiler и запускался в один поток на машине i5–2410M 2.3Ghz. Просто мне так удобнее — писать код лежа на не очень мощном ноутбуке, а 64-битный компилятор ставить лень. Замеры времени не блещут точностью, поскольку код редко запускался более 1 раза на замер, при этом другие процессы вроде браузера могли немного влиять на время работы. Однако для наших целей точность приемлемая.Сказка #1 за O (n5)
Давайте начнем с самого тупого решения, которое может быть. Код:
Код
long long gcd( long long x, long long y )
{
    while (x&&y) x>y ? x%=y : y%=x;
    return x+y;
}

void tale1( int n )
{
    for (int a=1; a<=n; a++)
        for (int b=a+1; b<=n; b++)
            for (int c=b+1; c<=n; c++)
                for (int d=c+1; d<=n; d++)
                    for (int e=d+1; e<=n; e++)
                    {
                        long long a5 = (long long)a*a*a*a*a;
                        long long b5 = (long long)b*b*b*b*b;
                        long long c5 = (long long)c*c*c*c*c;
                        long long d5 = (long long)d*d*d*d*d;
                        long long e5 = (long long)e*e*e*e*e;
                        if (a5 + b5 + c5 + d5 == e5)
                            if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1)
                                printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e );
                    }
}


На самом деле, это не самое тупое, ибо можно все переменные гонять от 1 до n и в конце проверять, что a
n Время
100 1563ms
200 40s
500 74m

Плюсы: простое как валенок, быстро пишется, требует O (1) памяти, находит классическое решение 275 + 845 + 1105 + 1335 = 1445.
Минусы: оно тормознутое.Сказка #2 за O (n4log n)
Давайте немного ускорим наше решение. По сути, этот вариант эквивалентен тому, что предложил товарищ drBasic.
Код
void tale2( int n )
{
    vector< pair< long long, int > > vec;
    for (int a=1; a<=n; a++)
        vec.push_back( make_pair( (long long)a*a*a*a*a, a ) );
    for (int a=1; a<=n; a++)
        for (int b=a+1; b<=n; b++)
            for (int c=b+1; c<=n; c++)
                for (int d=c+1; d<=n; d++)
                {
                    long long a5 = (long long)a*a*a*a*a;
                    long long b5 = (long long)b*b*b*b*b;
                    long long c5 = (long long)c*c*c*c*c;
                    long long d5 = (long long)d*d*d*d*d;
                    long long sum = a5+b5+c5+d5;
                    vector< pair< long long, int > >::iterator
                        it = lower_bound( vec.begin(), vec.end(), make_pair( sum, 0 ) );
                    if (it != vec.end() && it->first==sum)
                        if (gcd( a, gcd( gcd( b, c ), gcd( d, it->second ) ) ) == 1)
                            printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, it->second );
                }
}


Тут мы создаем массив, куда сохраняем пятые степени всех чисел от 1 до n, после чего внутри четырех вложенных циклов двоичным поиском проверяем есть ли число a5 + b5 + c5 + d5 в массиве или нет.
n Время #1 Время #2
100 1563ms 318ms
200 40s 4140ms
500 74m 189s
1000 55m

Этот вариант работает уже быстрее, у меня даже хватило терпения дождаться окончания работы программы для n=1000.

Плюсы: все еще довольно простое, быстрее тупого решения, несложно пишется, находит классическое решение.
Минусы: требует O (n) памяти, все еще тормознутое.

Сказка #3 за O (n4log n), но с O (1) памяти
На самом деле нет смысла хранить все степени в массиве и искать там что-то бинпоиском. Мы же и так знаем какое число в этом массиве на позиции i. Можно просто запустить бинпоиск на «виртуальном» массиве. Сказано — сделано:
Код
void tale3( int n )
{
    for (int a=1; a<=n; a++)
        for (int b=a+1; b<=n; b++)
            for (int c=b+1; c<=n; c++)
                for (int d=c+1; d<=n; d++)
                {
                    long long a5 = (long long)a*a*a*a*a;
                    long long b5 = (long long)b*b*b*b*b;
                    long long c5 = (long long)c*c*c*c*c;
                    long long d5 = (long long)d*d*d*d*d;
                    long long sum = a5+b5+c5+d5;
                    if (sum <= (long long)n*n*n*n*n)
                    {
                        int mi = d, ma = n; // invariant: for mi <, for ma >=
                        while ( mi+1 < ma )
                        {
                            int s = ((mi+ma)>>1);
                            long long tmp = (long long)s*s*s*s*s;
                            if (tmp < sum) mi = s;
                            else ma = s;
                        }
                        if (sum == (long long)ma*ma*ma*ma*ma)
                            if (gcd( a, gcd( gcd( b, c ), gcd( d, ma ) ) ) == 1)
                                printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, ma );
                    }
                }
}


Теперь массив не нужен, у нас чистый бинарный поиск.
n Время #1 Время #2 Время #3
100 1563ms 318ms 490ms
200 40s 4140ms 6728ms
500 74m 189s 352s
1000 55m

К сожалению, время выполнения просело, вероятно, из-за того, что внутри бинпоиска мы каждый раз заново вычисляем пятую степень. Ну и ладно.

Плюсы: требует O (1) памяти, находит классическое решение.
Минусы: тормознее предыдущего решения.

Сказка #4 за O (n4)
Давайте еще раз всмотримся в наше уравнение:

a5 + b5 + c5 + d5 = e5

или, для простоты A = B.

Пусть алгоритм выполняет наши 4 вложенных цикла. Зафиксируем значения a, b и с и посмотрим как себя ведут значения d и e. Пусть для какого-то d=x наименьшее значение e, для которого A<=B, равно y. Для d=x нам нет смысла рассматривать значения e>y. Заметим также, что для d=x+1 наименьшее значение e, для которого A<=B, не меньше y. То есть, мы можем всегда просто аккуратно увеличивать значение e пока идем по d и это гарантирует, что мы ничего не пропустим. Поскольку значения d и e только увеличиваются, общий проход по ним займет время O(n). Это идея называется методом двух указателей.

Код
void tale4( int n )
{
    for (int a=1; a<=n; a++)
        for (int b=a+1; b<=n; b++)
            for (int c=b+1; c<=n; c++)
            {
                int e = c+1;
                for (int d=c+1; d<=n; d++)
                {
                    long long a5 = (long long)a*a*a*a*a;
                    long long b5 = (long long)b*b*b*b*b;
                    long long c5 = (long long)c*c*c*c*c;
                    long long d5 = (long long)d*d*d*d*d;
                    long long sum = a5+b5+c5+d5;

                    while (e


Кода меньше, чем для бинпоиска, а пользы больше.
n Время #1 Время #2 Время #3 Время #4
100 1563ms 318ms 490ms 360ms
200 40s 4140ms 6728ms 4339ms
500 74m 189s 352s 177s
1000 55m 46m

Из-за большой скрытой константы это решение начинает обгонять решение #2 за O (n4log n) только при n порядка 500. Его, конечно же, можно ускорить, вычисляя пятые степени более обдуманно, но мы не будет этого делать.

Плюсы: асимптотически быстрее решения #2, требует O (1) памяти. Да, находит.
Минусы: далеко не самый оптимум, большая скрытая константа.

Сказка #5 за O (n3)
Давайте будем развивать идею с двумя указателями, а все остальное в решении перевернем вверх дном. Пусть у нас есть уравнение A+B=C, причем для каждого из A, B, C у нас есть n (A), n (B), n© способов их выбрать. Давайте зафиксируем какое-нибудь значение C, а все допустимые значения для A и B отсортируем по возрастанию. Тогда мы можем бежать по значениям A и B при помощи двух указателей и за O (n (A)+n (B)) проверить все что нужно для текущего значения С! А именно: для какого-то фиксированного A мы будем уменьшеать значение B, пока A+B>C. Как только станет A+B<=C, дальше B смысла уменьшать нет. Тогда мы увеличиваем A и продолжаем процесс уменьшения B. Весь алгоритм полностью займет время O( n(A) log n(A) + n(B) log n(B) + (n(A)+n(B)) n(С) ).

Для случая, когда A и B — элементы одного множества, алгоритм проверки зафиксированного C можно остановить как только текущие A и B встретятся (поскольку, без ограничения общности, можно считать, что A

Теперь в нашем уравнении обозначим (a5 + b5) за A, (c5 + d5) за B, а e5 за С. И напишем следующий код:

Код
void tale5( int n )
{
    vector< pair< long long, int > > vec;
    for (int a=1; a<=n; a++)
        for (int b=a+1; b<=n; b++)
        {
            long long a5 = (long long)a*a*a*a*a;
            long long b5 = (long long)b*b*b*b*b;
            if (a5 + b5 < (long long)n*n*n*n*n) // avoid overflow for n<=5000
                vec.push_back( make_pair( a5+b5, (a<<16)+b ) );
        }
    sort( vec.begin(), vec.end() );

    for (int e=1; e<=n; e++)
    {
        long long e5 = (long long)e*e*e*e*e;
        int i = 0, j = (int)vec.size()-1;
        while( i < j )
        {
            while ( i < j && vec[i].first + vec[j].first > e5 ) j--;
            if ( vec[i].first + vec[j].first == e5 )
            {
                int a = (vec[i].second >> 16);
                int b = (vec[i].second & ((1<<16)-1));
                int c = (vec[j].second >> 16);
                int d = (vec[j].second & ((1<<16)-1));
                if (b < c && gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1)
                    printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e );
            }
            i++;
        }
    }
}


Поскольку пар (a, b) (и (c, d)) у нас порядка n2, сортировка займет O (n2 log n), а дальшейшая проверка при помощи указателей — O (n3). Итого чистый куб.

Упражнение. Найдите логическую ошибку в коде выше.

Подумайте пару минут перед тем, как смотреть ответ.
В нашем случае в отсортированном массиве теоретически могут попасться одинаковые суммы и тогда два указателя могут пропустить некоторые равенства. Но на самом деле они будут все разные из следующих рассуждений: если будут совпадения, то x^5+y^5 = z^5+t^5 для некоторых x, y, z, t и мы нашли контрпример к этой гипотезе. В качестве исправления самое простое, что можно сделать — это проверить, что все числа действительно различны.

n #1 #2 #3 #4 #5
100 1563ms 318ms 490ms 360ms 82ms
200 40s 4140ms 6728ms 4339ms 121ms
500 74m 189s 352s 177s 516ms
1000 55m 46m 3119ms
2000 22s
5000 328s

Значительное ускорение позволяет затащить n=5000 за приемлемое время. Проверки при добавлении пар в массив нужны для избежания переполнения.

Плюсы: вероятно, самый быстрый алгоритм по асимптотике.
Минусы: большая скрытая константа, работает только до n порядка 5000, жрет аж O (n2) памяти.

Сказка #6 за O (n4 log n) с невероятно маленькой скрытой константой
Внезапно. С подачи пользователя erwins22 из этого комментария, рассмотрим остатки, которые мы можем получить при делении пятой степени на 11. То есть, какие a могут быть в сравнении x5=a mod 11. Оказывается, что возможные значения a — это 0, 1 и -1 (mod 11) (проверьте сами и убедитесь).

Тогда в равенстве a5 + b5 + c5 + d5 = e5 единиц и минус единиц суммарно четное количество (они должны друг друга уравновесить, чтобы четность сошлась), из этого следует, что одно из чисел a, b, c, d, e сравнимо с 0 до модулю 11, то есть делится на 11. Давайте вынесем его отдельно в одну сторону, получим один из двух вариантов:

(a5 + b5) + (c5 + d5) = e5; e = 0 mod 11

(e5 — a5) — (b5 + c5) = d5; d = 0 mod 11

Вы не поверите, но если число x делится на 11, то число x5 делится на 161051. Значит, на 161051 должна делиться и левая часть приведенных выше равенств. Как можно видеть, в уравнениях выше некоторые числа уже заботливо объединены в пары при помощи скобок. Теперь, если мы зафиксируем первую скобку, то вторая скобка может иметь только один из всевозможных 161051 остатков при делении на 161051. Таким образом, на каждую из O (n2) первых скобок в среднем приходится O (n2/161051) вторых. Если мы теперь переберем их все и посмотрим, является ли результат точной пятой степенью (например, биноиском в массиве пятых степеней) — то найдем все решения за O (n4 log n/161051). Код:

Код
void tale5( int n )
{
    vector< pair< long long, int > > vec;
    for (int a=1; a<=n; a++)
        for (int b=a+1; b<=n; b++)
        {
            long long a5 = (long long)a*a*a*a*a;
            long long b5 = (long long)b*b*b*b*b;
            if (a5 + b5 < (long long)n*n*n*n*n) // avoid overflow for n<=5000
                vec.push_back( make_pair( a5+b5, (a<<16)+b ) );
        }

    vector< pair< long long, int > > pows;
    for (int a=1; a<=n; a++)
        pows.push_back( make_pair( (long long)a*a*a*a*a, a ) );

    // a^5 + b^5 + c^5 + d^5 = e^5
    for (int a=1; a<=n; a++)
        for (int b=a+1; b<=n; b++)
        {
            long long a5 = (long long)a*a*a*a*a;
            long long b5 = (long long)b*b*b*b*b;
            long long rem = (z - (a5+b5)%z)%z;
            for (int i=0; i<(int)vec[rem].size(); i++)
            {
                long long sum = a5 + b5 + vec[rem][i].first;
                vector< pair< long long, int > >::iterator
                    it = lower_bound( pows.begin(), pows.end(), make_pair( sum, 0 ) );
                if (it != pows.end() && sum == it->first)
                {
                    int c = (vec[rem][i].second >> 16);
                    int d = (vec[rem][i].second & ((1<<16)-1));
                    int e = it->second;
                    if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1)
                        printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e );
                }
            }
        }

    // e^5 - a^5 - b^5 - c^5 = d^5
    for (int e=1; e<=n; e++)
        for (int a=1; a vec[rem][i].first)
                {
                    long long sum = e5 - a5 - vec[rem][i].first;
                    vector< pair< long long, int > >::iterator
                        it = lower_bound( pows.begin(), pows.end(), make_pair( sum, 0 ) );
                    if (it != pows.end() && sum == it->first)
                    {
                        int b = (vec[rem][i].second >> 16);
                        int c = (vec[rem][i].second & ((1<<16)-1));
                        int d = it->second;
                        if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1)
                            printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e );
                    }
                }
        }
}


Время работы работы данного решения:
n #1 #2 #3 #4 #5 #6
100 1563ms 318ms 490ms 360ms 82ms 129ms
200 40s 4140ms 6728ms 4339ms 121ms 140ms
500 74m 189s 352s 177s 516ms 375ms
1000 55m 46m 3119ms 2559ms
2000 22s 38s
5000 328s 28m

Из таблицы видно, что для n=500 и n=1000 это решение даже обгоняет кубическое. Но затем кубическое решение все же начинает сильно обгонять. Асимптотика она такая — ее не обманешь.

Плюсы: очень мощное отсечение.
Минусы: большая асимптотика, непонятно как прикрутить эту идею к кубическому решению.

Сказка #7 за O (n3) co 128-битными числами
Давайте пока временно забудем про трюки с модулями (мы обязательно из вспомним чуть позже!) и переделаем наше кубическое решение, чтобы оно могло корректно работать для n>5000. Для этого реализуем 128-битные целые числа.
Код
typedef unsigned long long uint64;
typedef pair< uint64, uint64 > uint128;

uint128 operator+ (const uint128 & a, const uint128 & b)
{
    uint128 re = make_pair( a.first + b.first, a.second + b.second );
    if ( re.second < a.second ) re.first++;
    return re;
}

uint128 operator- (const uint128 & a, const uint128 & b)
{
    uint128 re = make_pair( a.first - b.first, a.second - b.second );
    if ( re.second > a.second ) re.first--;
    return re;
}

uint128 power5( int x )
{
    uint64 x2 = (uint64)x*x;
    uint64 x3 = (uint64)x2*x;
    uint128 re = make_pair( (uint64)0, (uint64)0 );
    uint128 cur = make_pair( (uint64)0, x3 );
    for (int i=0; i<63; i++)
    {
        if ((x2>>i)&1) re = re + cur;
        cur = cur + cur;
    }
    return re;
}

void tale7( int n )
{
    vector< pair< uint128, int > > vec = vector< pair< uint128, int > >( n*n/2 );
    uint128 n5 = power5( n );
    int ind = 0;
    for (int a=1; a<=n; a++)
        for (int b=a+1; b<=n; b++)
        {
            uint128 a5 = power5( a );
            uint128 b5 = power5( b );
            if (a5 + b5 < n5)
                vec[ind++] = make_pair( a5+b5, (a<<16)+b );
        }
    sort( vec.begin(), vec.begin()+ind );

    for (int e=1; e<=n; e++)
    {
        uint128 e5 = power5( e );
        int i = 0, j = ind-1;
        while( i < j )
        {
            while ( i < j && vec[i].first + vec[j].first > e5 ) j--;
            if ( vec[i].first + vec[j].first == e5 )
            {
                int a = (vec[i].second >> 16);
                int b = (vec[i].second & ((1<<16)-1));
                int c = (vec[j].second >> 16);
                int d = (vec[j].second & ((1<<16)-1));
                if (b < c && gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1)
                    printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e );
            }
            i++;
        }
    }
}


Операции, которые потребовалось дописать — сложение и возведение в пятую степень. Еще есть вычитание, в этом решении оно не нужно, но оно понадобится позже. Поэтому пусть будет. Так как 128-битное число реализовано как pair, там уже есть операции <, >, =, причем они работают именно так, как нам нужно.

В самом начале мы сразу задаем размер вектора. Не то, чтобы это сделано для оптимизации, просто мне пока лень расчехлять 64-битный компилятор, а на 32 битах доступно только 2Гб памяти. Сейчас для n=10000 требуется около 1.2Гб на вектор. Если расширять вектор через push_back, то он под самый конец захватывает больше 2Гб при реаллокации (чтобы увеличиться с длины N до 2*N нужно 3*N промежуточной памяти).

n #1 #2 #3 #4 #5 #6 #7
100 1563ms 318ms 490ms 360ms 82ms 129ms 20ms
200 40s 4140ms 6728ms 4339ms 121ms 140ms 105ms
500 74m 189s 352s 177s 516ms 375ms 1014ms
1000 55m 46m 3119ms 2559ms 7096ms
2000 22s 38s 52s
5000 328s 28m 13m
10000 89m

Можно видеть, что теперь программа замедлилась почти ровно в 2 раза относительно решения #5, зато мы покорили новую неприступную вершину n=10000!

Плюсы: теперь не переполняется для n>5000.
Минусы: работает в 2 раза медленнее решения #5, жрет кучу памяти.

Сказка #8 за O (n3) с меньшей скрытой константой
Вспомним опять про остатки при делении на 11. Имеем два равенства:

(a5 + b5) + (c5 + d5) = e5; e = 0 mod 11

(e5 — a5) — (b5 + c5) = d5; d = 0 mod 11

Напомним, что пятые степени по модулю 11 всегда имеют остатки 0, 1 или -1. Снимем ограничения вида a < b < c < d и позволим числам произвольно перемещаться из одной скобки в другую. Тогда несложно показать (рассмотрением всех случаев), что их всегда можно переместить так, что каждая из скобок будет равна 0 по модулю 11. Ну и теперь нам нужно будет перебрать все пары чисел от 1 до n, найти сумму и разность их пятых степеней и запомнить только те, которые делятся на 11. А остальные пары можно просто выкинуть.

Можно сформулировать такой факт: число таких пар будет порядка 51/121 от общего числа пар (подумайте почему это так). К сожалению, нам нужно будет сохранить два массива таких пар (для суммы и для разности), что даст выигрыш по памяти только 102/121. Ну, 15% — это тоже сокращение. Зато далее нам по этим массивам надо будет чуть меньше бегать.

Ну и, наконец, самые хорошие новости: теперь нам имеем смысл одну из переменных (которая самая внешняя в кубическом решении) перебирать с шагом в 11. Плохие новости в том, что надо будет отдельно решать оба вида равенств. Самое печальное во всем этом: увы, это ускорит программу всего в 11 раз (на самом деле, пока не факт), вместо 115 раз, как в решении #6.

Код
void tale8( int n )
{
    vector< pair< uint128, pair< int, int > > > vec_p, vec_m;
    uint128 n5 = power5( n );
    for (int a=1; a<=n; a++)
        for (int b=1; b e5 ) j--;
            if ( vec_p[i].first + vec_p[j].first == e5 )
            {
                int a = vec_p[i].second.first;
                int b = vec_p[i].second.second;
                int c = vec_p[j].second.first;
                int d = vec_p[j].second.second;
                if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1)
                    printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e );
            }
            i++;
        }
    }

    // (e^5 - a^5) - (b^5 + c^5) = d^5
    for (int d=11; d<=n; d+=11)
    {
        uint128 d5 = power5( d );
        int i = 0, j = 0, mx_i = (int)vec_m.size(), mx_j = (int)vec_p.size();
        while (i < mx_i && j < mx_j)
        {
            while (j < mx_j && vec_m[i].first > vec_p[j].first && vec_m[i].first - vec_p[j].first > d5) j++;
            if ( j < mx_j && vec_m[i].first > vec_p[j].first && vec_m[i].first - vec_p[j].first == d5 )
            {
                int e = vec_m[i].second.first;
                int a = vec_m[i].second.second;
                int b = vec_p[j].second.first;
                int c = vec_p[j].second.second;
                if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1)
                    printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e );
            }
            i++;
        }
    }
}


Тут с реаллокацией векторов повезло больше и программа для n=10000 укладывается в 2Гб.
n #1 #2 #3 #4 #5 #6 #7 #8
100 1563ms 318ms 490ms 360ms 82ms 129ms 20ms 16ms
200 40s 4140ms 6728ms 4339ms 121ms 140ms 105ms 49ms
500 74m 189s 352s 177s 516ms 375ms 1014ms 472ms
1000 55m 46m 3119ms 2559ms 7096ms 2110ms
2000 22s 38s 52s 13s
5000 328s 28m 13m 161s
10000 89m 20m

Увы и ах, программу ускорилась всего в 4,5 раз. Видать, многочисленные проверки во втором уравнении сильно подпортили скрытую константу. Ну ничего, тут еще есть простор для оптимизаций. Самая большая проблема сейчас: дикое потребление памяти. Если по времени для текущего рекорда n уже терпимо, то по памяти мы уже не влезаем.

Плюсы: наверно, самое быстрое решение из предложенных.
Минусы: все еще проблема с большим потреблением памяти.

Сказка #9 за O (n3log n) с потреблением памяти O (n)
Как же нам уменьшить потребление памяти? Давайте воспользуемся трюком, описанным здесь. А именно: давайте возьмем какое-нибудь простое число p, большее n, но не намного. Рассмотрим первое уравнение, которое у нас есть (второе уравнение рассматривается аналогично):

(a5 + b5) + (c5 + d5) = e5; e = 0 mod 11

Теперь пусть (a5 + b5) = w mod p для какого-то w от 0 до p-1. Тогда число пар (a, b), которые удовлетворяют данному сравнению — линейное количество. Чтобы показать это, давайте переберем параметр a от 1 до n. Тогда, чтобы найти b, нам надо будет решить сравнение b5 = (w — a5) = u mod p. И утверждается, что у этого сравнения всегда будет не более одного решения. Следует это вот из этой страницы на e-maxx. Там нужно обратить внимание на формулу получения всех решений из одного:

90e6c5ea5b674fe382014b8008dcd94f.png

То есть, всего решений у нас gcd (5, phi (p)) = gcd (5, p-1). Отсюда получаем, что если p=5q+1, то у нас 5 решений (или ни одного), а в остальных случаях — решений не более, чем одно.

(Кстати, я понятия не имею откуда эта формула берется и как она работает. Если кто знает источник, где это доходчиво описано — просьба поделиться ссылкой.)

Теперь вопрос — как найти для фиксированного u значение b? Чтобы сделать это единоразово, но быстро — нужно довольно сильно разбираться в теории чисел. Но нам нужны b для всех возможных значений u, поэтому можно просто для каждого b найти u, и записать в табличку: вот для такого u — такое решение b.

Далее, для фиксированного w и фиксированного e5, получаем, что (c5 + d5) = (e5 — w) mod p. Тут тоже линейное количество пар, удовлетворяющих сравнению.

То есть, для фиксированного w и фиксированного e мы получаем линейное количество пар, которые нужно отсортировать (к сожалению, здесь вылезает лишний логарифм в асимптотике), после чего пройтись двумя указателями. Поскольку различных значений w и e порядка O (n), общая асимптотика получается O (n3log n).

Давайте напишем пробный страшный код:

Код
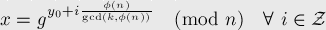
bool is_prime( int x )
{
    if (x<2) return false;
    for (int a=2; a*a<=x; a++)
        if (x%a==0)
            return false;
    return true;
}

void tale9( int n )
{
    int p = n+1;
    while ( p%5==1 || !is_prime( p ) ) p++;

    vector< int > sols = vector< int >( p, -1 );
    for (int i=1; i<=n; i++)
    {
        uint64 tmp = ((uint64)i*i)%p;
        tmp = (((tmp*tmp)%p)*i)%p;
        sols[(unsigned int)tmp] = i;
    }

    for (int w=0; w > > vec1;

        for (int a=1; a<=n; a++)
        {
            uint64 a5p = ((uint64)a*a)%p;
            a5p = ((a5p*a5p)%p*a)%p;
            int b = sols[ (w - a5p + p)%p ];
            if (b!=-1 && b > > vec2;

            for (int c=1; c<=n; c++)
            {
                uint64 c5p = ((uint64)c*c)%p;
                c5p = ((c5p*c5p)%p*c)%p;
                int d = sols[ (q - c5p + p)%p ];
                if (d!=-1 && d= 0 )
            {
                while ( j >= 0 && vec1[i].first + vec2[j].first > e5 ) j--;
                if ( j >= 0 && vec1[i].first + vec2[j].first == e5 )
                {
                    int a = vec1[i].second.first;
                    int b = vec1[i].second.second;
                    int c = vec2[j].second.first;
                    int d = vec2[j].second.second;
                    if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1)
                        printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e );
                }
                i++;
            }
        }

        // (e^5 - a^5) - (b^5 + c^5) = d^5
        // (b^5 + c^5) = w  (mod p)
        // already computed as vec1
        for (int d=11; d<=n; d+=11)
        {
            // (e^5 - a^5) = (d^5 + w) = q  (mod p)
            uint64 d5p = ((uint64)d*d)%p;
            d5p = ((d5p*d5p)%p*d)%p;
            int q = (int)((d5p + w)%p);
            vector< pair< uint128, pair< int, int > > > vec2;

            for (int e=1; e<=n; e++)
            {
                uint64 e5p = ((uint64)e*e)%p;
                e5p = ((e5p*e5p)%p*e)%p;
                int a = sols[ (e5p - q + p)%p ];
                if (a!=-1 && a vec1[j].first && vec2[i].first - vec1[j].first > d5) j++;
                if ( j < mx_j && vec2[i].first > vec1[j].first && vec2[i].first - vec1[j].first == d5 )
                {
                    int e = vec2[i].second.first;
                    int a = vec2[i].second.second;
                    int b = vec1[j].second.first;
                    int c = vec1[j].second.second;
                    if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1)
                        printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e );
                }
                i++;
            }
        }
    }
}


Запускаем эту жестокую жесть:
n #1 #2 #3 #4 #5 #6 #7 #8 #9
100 1563ms 318ms 490ms 360ms 82ms 129ms 20ms 16ms 219ms
200 40s 4140ms 6728ms 4339ms 121ms 140ms 105ms 49ms 1741ms
500 74m 189s 352s 177s 516ms 375ms 1014ms 472ms 25s
1000 55m 46m 3119ms 2559ms 7096ms 2110ms 200s
2000 22s 38s 52s 13s 28m
5000 328s 28m 13m 161s
10000 89m 20m

Господа, добро пожаловать снова в каменный век! Что ж оно так тормозит-то безбожно? Ах да, там же теперь функция power5() на самом дне трех вложенных циклов, внутри которой цикл аж на 63 итерации. Переписывать на интринсики? Спокойно, в следующем решении мы просто будем тащить ответ из предпосчитанной таблички.

Зато теперь оно почти не ест память, а также появилось одно очень полезное свойство: теперь задачу можно разбить на независимые подзадачи, то есть «распараллелить», а точнее — распределить вычисления на несколько ядер. А именно: для каждого ядра давать свои значения параметра w и при покрытии этими w всех чисел от 0 до p-1 мы покроем все случаи в задаче, при этом нагрузка на все ядра будет распределена примерно равномерно.

Плюсы: потребляет очень мало памяти, поддерживает распределенные вычисления.
Минусы: тормозит как сапожник с похмелья.

Сказка #10 за O (n3log n) с хардкорными оптимизациями
Берем решение #9 и добавляем хардкорные оптимизации. Ну, на самом деле, не такие уж они и хардкорные. Но их много:
  • Предпросчитываем все, что только можно предпосчитать и выносим в таблички.
  • Отказываемся от векторов с их push_back-ами и переделываем все на статичные массивы.
  • Везде, где только можно, убираем операции взятия остатка от деления.
  • В массивах для пар теперь храним только сумму (или разность) пятых степеней, а сами пары пытаемся восстановить только если найдено решение (так как решения очень редки — пара ищется втупую за квадрат).
  • Массивы, которые генерируются внутри циклов по e и d теперь в среднем в 2 раза короче. Действительно, для случая (a5 + b5) + (c5 + d5) = e5 нам интересны только (c5 + d5) < e5 (хорошо при малых e), а для (e5 — a5) — (b5 + c5) = d5 нам интересны только (e5 — a5) > d5 (хорошо при больших d).

И получаем код:
Код
#define MAXN 100500

int pow5modp[MAXN];
int sols[MAXN];
uint128 vec1[MAXN], vec2[MAXN];
int vec1_sz, vec2_sz;
uint128 pow5[MAXN];
int pow5mod11[MAXN];

void init_arrays( int n, int p )
{
    for (int i=1; i<=n; i++)
    {
        uint64 i5p = ((uint64)i*i)%p;
        i5p = (((i5p*i5p)%p)*i)%p;
        pow5modp[i] = (int)i5p;
    }

    for (int i=0; i= 0 )
            {
                while ( j >= 0 && vec1[i] + vec2[j] > e5 ) j--;
                if ( j >= 0 && vec1[i] + vec2[j] == e5 )
                {
                    int a=-1, b=-1, c=-1, d=-1;
                    for (int A=1; A<=n; A++)
                        for (int B=1; B d5) vec2[vec2_sz++] = s;
                    }
            }

            sort( vec2, vec2 + vec2_sz );

            int i = 0, j = 0, mx_i = vec2_sz, mx_j = vec1_sz;
            while (i < mx_i && j < mx_j)
            {
                while (j < mx_j && vec2[i] > vec1[j] && vec2[i] - vec1[j] > d5) j++;
                if ( j < mx_j && vec2[i] > vec1[j] && vec2[i] - vec1[j] == d5 )
                {
                    int e=-1, a=-1, b=-1, c=-1;
                    for (int E=1; E<=n; E++)
                        for (int A=1; A


Код стал компактнее, проще и добрее, что ли. А еще он стал быстрее:
n #1 #2 #3 #4 #5 #6 #7 #8 #9 #10
100 1563ms 318ms 490ms 360ms 82ms 129ms 20ms 16ms 219ms 8ms
200 40s 4140ms 6728ms 4339ms 121ms 140ms 105ms 49ms 1741ms 30ms
500 74m 189s 352s 177s 516ms 375ms 1014ms 472ms 25s 379ms
1000 55m 46m 3119ms 2559ms 7096ms 2110ms 200s 2993ms
2000 22s 38s 52s 13s 28m 24s
5000 328s 28m 13m 161s 405s
10000 89m 20m 59m

Мы проверили все варианты для n=10000 за более-менее приемлемое время, используя какие-то жалкие 10 Мб памяти.

Плюсы: достаточно быстрое, ест мало памяти.
Минусы: их нет.

Ни в сказке сказать, ни пером описать
А ТЕПЕРЬ я достаю из широких штанин 64-битный компилятор, 6-ядерный i7–5820K 3.3GHz и 4-ядерный i7–3770 3.4GHz и запускаю решение #10 в 16 независимых потоков на несколько дней.
n Суммарно по ядрам Реального времени Потоков
10000 29m 29m 1
20000 318m 58m 6
50000 105h 7h 16
100000 ожидается ~960h (80% done*) ожидается ~60h (80% done*) 16

* прошу меня простить за мое нетерпение, я напишу точные цифры когда оно досчитает.

64-битная программа на более быстрой машине (напомню, ранее я тестировал код на i5–2410M 2.3Ghz) работает примерно в 2 раза быстрее. В итоге удалось затащить n=100000 и найти** второе решение искомого диофантова уравнения:

555 + 31835 + 289695 + 852825 = 853595

** Перед тем, как начать финальные рассчеты, я вычислил для какого w ответ будет найден, после чего проверил его — и все сошлось.

Сказка — ложь, да в ней намек
Вот так вот не самое быстрое решение с не самой быстрой асимптотикой бывает лучше всего на практике.

По идее, код можно ускорить еще или отрезать логарифм от асимптотики, но на текущий момент мне пока надоело оптимизировать — я уже потерял достаточно времени. Насчет логарифма решения два: заменить быструю сортировку на radix sort (но тогда константа возрастет до космических размеров), либо вместо идеи двух указателей использовать хэш-таблицу (тут уже надо писать и смотреть что действительно быстрее). Профилировка показала, что для n=10000 сортировка занимает примерно половину всего времени, то есть для наших маленьких значений n логарифм довольно терпимый. Насчет ускорения: наверняка есть еще какие-нибудь трюки с модулями, позволяющие ускорить программу в 5–10 раз.

Затащим?
Еще у меня есть дикая идея проверить все n вплоть до миллиона. Ожидаемое время проверки, в принципе, реальное — около миллиона ядрочасов. Но моих мощностей для этого будет явно недостаточно. Затащим вместе? Впрочем, я не нашел информации о том, до какого n уже все перебрали. Может до миллиона искать уже нет смысла, ибо все давно посчитано. Прошу отписаться, если у кого есть информация по этому поводу.

Тут и сказочке конец, кто осилил — молодец!

Комментарии (4)

  • 27 декабря 2016 в 09:26 (комментарий был изменён)

    0

    ↑

    ↓

    Найдите логическую ошибку в коде выше.
    while( i < j )
        {
            while ( i < j && vec[i].first + vec[j].first > e5 ) j--;
            if ( vec[i].first + vec[j].first == e5 )
            {
                bla bla = bla;
            }
            i++;
        }

    Я правильно понимаю, что во втором случае условие выглядит так: 
    while ( 1 && vec[i].first + vec[j].first > e5 ) j--;

    А ещё, не замедляет ли решение printf, как было в одной из предыдущих статей на эту тему?

    • 27 декабря 2016 в 09:51

      0

      ↑

      ↓

      Там же происходит j--, поэтому в процессе выполнения цикла условие i < j может нарушиться.
      По хорошему, i < j надо вставить еще в следующий if, но когда это не выполняется, будет i=j и, в принципе, индекс массива j остается валидный.

      • 27 декабря 2016 в 10:07

        0

        ↑

        ↓

        Да, точно. Не увидел сразу, что весь цикл одной строчкой.
        Ещё я&

        © Habrahabr.ru