[recovery mode] Почему топовым физикам не нравятся голые сингулярности

Роджер Пенроуз стал лауреатом Нобелевской премии по физике 2020 года за теоремы о формировании черных дыр, которые он доказал совместно с Хокингом еще в 1960–70х годах. Поздравляем!
Однако главной заслугой Пенроуза в этом направлении является то, что он в свое время сделал теорию гравитации Эйнштейна (общую теорию относительности) мейнстримом. До Пенроуза считалось, что теорией относительности не стоит заниматься молодым физикам. В ней не осталось интересных проблем. Это старая, созданная еще в 1916 г., теория уже исследована вдоль и поперек.
Пенроуз показал, что это не так. Он развил новые математические методы (диаграммы Пенроуза) и получил множество интересных результатов. Он положил начало золотому веку черных дыр, кульминацией которого принято считать открытие эффекта испарения черных дыр посредством излучения Хокинга. Одним из результатов того плодотворного периода является и его гипотеза космической цензуры, согласно которой голые сингулярности запрещены Природой.
Сингулярности
Сингулярностью называется точка (или область) в которой некоторая величина становится бесконечной. В отличие от нуля, бесконечность с физической точки зрения — это плохо. Бесконечность нельзя измерить никаким прибором, она ненаблюдаема и поэтому нефизична.
Однако с математической точки зрения в бесконечностях нет ничего особенного. Георг Кантор даже создал для них арифметику. Но для нашего последующего изложения целесообразно привести пример математического объекта, имеющего точку с бесконечной кривизной — сингулярностью. Простейшим примером является конус:
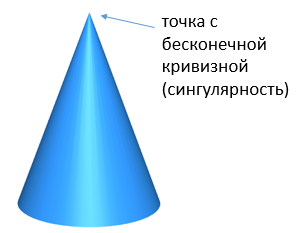
Если найти количественную меру кривизны в виде тензора кривизны Римана, то окажется, что он равен нулю везде кроме одной единственной точки — вершины конуса, где кривизна становится бесконечной. Это и есть сингулярность. В данном случае с физической точки зрения ничего страшного не происходит, поскольку реальные конусы состоят из атомов и идеально острой вершины менее радиуса атома сделать не получится.
Общая теория относительности описывает гравитацию как искривление пространства-времени. Математически гравитационное поле характеризуется метрикой, которая находится решением уравнения Эйнштейна при заданных условиях. Так для сферически-симметричных гравитирующих тел (планеты, звезды, черные дыры) метрика, называемая метрикой Шварцшильда, выглядит следующим образом:
Заметьте, что при радиусе метрика становится сингулярной. Множитель при
обращается в ноль, а при
в бесконечность. Данный радиус называется горизонтом событий черной дыры.
Мы наблюдаем так называемую координатную сингулярность. Если найти тензор кривизны из данной метрики, то он не будет бесконечным на горизонте событий. Вообще-то он будет стремиться к нулю при увеличении массы черной дыры. Данная сингулярность является следствием выбранной системы координат. От нее можно избавиться перейдя к другим координатам.
Но в центре черной дыры () кривизна получится бесконечной. Это и есть сингулярность черной дыры.
До Пенроуза считалось, что это просто особенность математики и в реальных условиях никакой черной дыры не может образоваться. Сам термин «черная дыра» был введен Джоном Уилером только в 1967 г. Однако теоремы Пенроуза и Хокинга показали, что для некоторых звезд формирование черных дыр неизбежно. И как только горизонт событий сформировался, все что находится за ним обречено двигаться по направлению к сингулярности и закончить свое существование там. Избежать попадание в сингулярность всего, что находится за горизонтом событий невозможно.
По аналогии с рассмотренным примером с конусом можно конечно сказать, что появление сингулярности — это математическая особенность общей теории относительности. Квантовые эффекты должны сгладить бесконечную плотность в точке. И это один из возможных вариантов. Однако Пенроуз мыслил по-другому.
Голые сингулярности
Роджер Пенроуз предположил, что в рассмотренной нами метрике Шварцшильда сингулярность оказалась окруженной горизонтом событий не случайно. Горизонт призван скрывать сингулярность от наблюдателей. Согласно общей теории относительности он работает как однонаправленный шлюз, пропуская материю и свет только в одну сторону. Выбраться из черной дыры невозможно. И Пенроуз предположил, что это закон Природы:
Все сингулярности в Природе должны быть скрыты за горизонтами событий
Будучи европейцем, ценящим европейские ценности, Пенроуз решил назвать данную идею принципом космической цензуры.
Для метрики Шварцшильда гипотеза тривиально верна. Однако ценность ее в том, что если предположить ее верность, то она может служить фильтром, позволяющим отделить реально возможные конфигурации пространства-времени от искусственных, не реализуемых в Природе.
При разных конфигурациях начальных условий возможно получить разные сингулярности, например в форме кольца в метрике Керра. Также не составляет труда подобрать такие условия, что сингулярность получится голой — не окруженной горизонтом. Пенроуз надеется, что в реальных условиях Природа не может такого допустить.
Это схоже с тем как Курт Гедель получил решения уравнения Эйнштейна с замкнутыми времениподобными кривыми в которых время течет по кругу. Однако такие траектории в пространстве-времени никогда не получаются в реальных условиях эволюции нашей Вселенной. Другой пример — это начальная конфигурация клеточного автомата, которая не могла быть получена никакой предыдущей эволюцией. Принцип космической цензуры (если верен) позволяет отделить такие фейковые конфигурации от гипотетически возможных.
На данный момент идея Пенроуза остается в статусе гипотезы, то есть еще не доказана и может оказаться ложной. Но, как и в случае гипотезы Римана, имеется множество нетривиальных примеров, говорящих в пользу принципа космической цензуры.
Гипотеза слабой гравитации
В 2007 году молодой гарвардский физик-теоретик Любош Мотль с соавторами опубликовал известную сейчас работу в которой излагается схожая гипотеза, получившая название weak gravity conjecture. Из аргументов теории струн они предположили, что гравитация должна являться наиболее слабой силой Природы.
Любош Мотль — один из авторов гипотезы слабой гравитации
Опять же, с первого взгляда может показаться, что гипотеза тривиально верна. Ведь нам уже известно, что гравитация — это самая слабая из сил Природы. Но ведь нельзя исключить, что существуют и другие, еще не открытые силы. К тому же, как и в случае принципа космической цензуры, несложно придумать такие эффективные квантовые теории поля в которых гипотеза оказывается неверна.
Также как и принцип космической цензуры, гипотеза слабой гравитации в случае верности может служить в качестве фильтра. Она позволяет выбрать из множества допустимых квантовых теорий поля те, которые не противоречат теории струн и, следовательно, заслуживают внимания.
Удивительно, но гипотеза слабой гравитации тесно связана с принципом космической цензуры Пенроуза. Было показано, что последнее следует из первого. Но это не точно)
P.S. Продвижение европейских ценностей и политкорректности в США привело к тому, что Любош Мотль был вынужден покинуть Гарвард и разорвать контакты с научным сообществом на пике своей научной карьеры, в том же 2007 г.
В этом он схож с другим гением — математиком Александром Гротендиком, который оставил мир науки по политическим причинам когда ему было всего 42.
