[Перевод - recovery mode ] Руководство по SQL: Как лучше писать запросы (Часть 2)08.09.2019 12:02

Продолжение статьи Руководство по SQL: Как лучше писать запросы (Часть 1)

От запроса к планам выполнения


0i6sacyjz9j7pwvkqhfnr6ryjby.jpeg Зная, что антипаттерны не статичны и эволюционируют по мере того, как вы растете как разработчик SQL, и тот факт, что есть много, что нужно учитывать, когда вы задумываетесь об альтернативах, также означает, что избежать антипаттернов и переписывания запросов может быть довольно сложной задачей. Любая помощь может пригодиться, и именно поэтому более структурированный подход к оптимизации запроса с помощью некоторых инструментов может быть наиболее эффективным.

Следует также отметить, что некоторые из антипаттернов, упомянутых в последнем разделе, коренятся в проблемах производительности, таких, как операторы AND, OR и NOT и их отсутствие при использовании индексов. Размышление о производительности требует не только более структурированного, но и более глубокого подхода.

Однако этот структурированный и углубленный подход будет в основном основан на плане запроса, который, как вы помните, является результатом запроса, впервые проанализированного в «дерево синтаксического анализа» или «дерево разбора» («parse tree»), и точно определяет, какой алгоритм используется для каждой операции и как координируется их выполнение.

Оптимизация запросов


Как вы прочитали во введении, может потребоваться проверить и настроить планы, которые составляются оптимизатором вручную. В таких случаях вам нужно будет снова проанализировать ваш запрос, посмотрев на план запроса.

Чтобы получить доступ к этому плану, необходимо использовать инструменты, предоставляемые системой управления базами данных. В вашем распоряжении могут быть следующие инструменты:

  • Некоторые пакеты содержат инструменты, которые генерируют графическое представление плана запроса. Рассмотрим следующий пример:

    1yffwafdtmxfgdeanejdy5wjelo.gif

  • Другие инструменты позволят предоставить текстовое описание плана запроса. Одним из примеров является инструкция EXPLAIN PLAN в Oracle, но имя инструкции зависит от СУБД, с которой вы работаете. В другом месте можно найти EXPLAIN (MySQL, PostgreSQL) или EXPLAIN QUERY PLAN (SQLite).


Обратите внимание на то, что при работе с PostgreSQL можно сделать различие между EXPLAIN, где вы просто получаете описание, в котором говорится о том, как плановик намеревается выполнить запрос без его выполнения, в то время как EXPLAIN ANALYZE фактически выполняет запрос и возвращает вам анализ ожидаемых и фактических планов запроса. Вообще говоря, реальный план выполнения — это план, в котором фактически выполняется запрос, в то время как оценочный план выполнения определяет, что он будет делать без выполнения запроса. Хотя это логически эквивалентно, фактический план выполнения намного полезнее, поскольку он содержит дополнительные сведения и статистику о том, что действительно произошло при выполнении запроса.

В остальной части этого раздела вы узнаете больше о EXPLAIN и ANALYZE, а также о том, как использовать их для получения дополнительной информации о плане запроса и его возможной производительности. Для этого начните с нескольких примеров, в которых вы будете работать с двумя таблицами: one_million и half_million.

Вы можете получить текущую информацию из таблицы one_million с помощью EXPLAIN; Обязательно поместите его прямо над запросом, и после его выполнения он вернет вам план запроса: 

EXPLAIN
SELECT *
FROM one_million;

QUERY PLAN
____________________________________________________
Seq Scan on one_million
(cost=0.00..18584.82 rows=1025082 width=36)
(1 row)


В этом случае вы видите, что стоимость запроса равна 0.00..18584.82, а количество строк равно 1025082. Ширина числа столбцов равна 36.

Кроме того, вы можете обновить статистическую информацию с помощью ANALYZE.

ANALYZE one_million;
EXPLAIN
SELECT *
FROM one_million;

QUERY PLAN
____________________________________________________
Seq Scan on one_million
(cost=0.00..18334.00 rows=1000000 width=37)
(1 row)


Помимо EXPLAIN и ANALYZE, вы также можете получить фактическое время выполнения с помощью EXPLAIN ANALYZE: 

EXPLAIN ANALYZE
SELECT *
FROM one_million;

QUERY PLAN
___________________________________________________________
Seq Scan on one_million
(cost=0.00..18334.00 rows=1000000 width=37)
(actual time=0.015..1207.019 rows=1000000 loops=1)
Total runtime: 2320.146 ms
(2 rows)


Недостатком использования EXPLAIN ANALYZE является то, что запрос выполняется фактически, поэтому будьте осторожны с этим!

До сих пор все алгоритмы, которые вы видели, — это Seq Scan (Sequential Scan) или Full Table Scan: это сканирование, выполненное в базе данных, где каждая строка сканируемой таблицы читается в последовательном (serial) порядке, и найденные столбцы проверяются на предмет соответствия условию или нет. Что касается производительности, последовательное сканирование, безусловно, не лучший план выполнения, потому что вы все еще выполняете полное сканирование таблицы (full table scan). Тем не менее, это не так уж плохо, когда таблица не помещается в память: последовательное чтение выполняется довольно быстро даже на медленных дисках.

Об этом вы узнаете позже, когда будем говорить о сканировании индекса (index scan).

Однако есть и другие алгоритмы. Возьмем, например, этот план запроса для соединения: 

EXPLAIN ANALYZE
SELECT *
FROM one_million JOIN half_million
ON (one_million.counter=half_million.counter);
QUERY PLAN
_________________________________________________________________
Hash Join (cost=15417.00..68831.00 rows=500000 width=42)
(actual time=1241.471..5912.553 rows=500000 loops=1)
Hash Cond: (one_million.counter = half_million.counter)
    -> Seq Scan on one_million
    (cost=0.00..18334.00 rows=1000000 width=37)
    (actual time=0.007..1254.027 rows=1000000 loops=1)
    -> Hash (cost=7213.00..7213.00 rows=500000 width=5)
    (actual time=1241.251..1241.251 rows=500000 loops=1)
    Buckets: 4096 Batches: 16 Memory Usage: 770kB
    -> Seq Scan on half_million
    (cost=0.00..7213.00 rows=500000 width=5)
(actual time=0.008..601.128 rows=500000 loops=1)
Total runtime: 6468.337 ms


Вы видите, что оптимизатор запросов выбрал здесь Hash Join! Запомните эту операцию, так как она понадобится вам для оценки временной сложности вашего запроса. Пока что обратите внимание, что в half_million.counter нет индекса, который добавим в следующем примере: 

CREATE INDEX ON half_million(counter);
EXPLAIN ANALYZE
SELECT *
FROM one_million JOIN half_million
ON (one_million.counter=half_million.counter);
QUERY PLAN
________________________________________________________________
Merge Join (cost=4.12..37650.65 rows=500000 width=42)
(actual time=0.033..3272.940 rows=500000 loops=1)
Merge Cond: (one_million.counter = half_million.counter)
    -> Index Scan using one_million_counter_idx on one_million
    (cost=0.00..32129.34 rows=1000000 width=37)
    (actual time=0.011..694.466 rows=500001 loops=1)
    -> Index Scan using half_million_counter_idx on half_million
    (cost=0.00..14120.29 rows=500000 width=5)
(actual time=0.010..683.674 rows=500000 loops=1)
Total runtime: 3833.310 ms
(5 rows)


Вы видите, что, создав индекс, оптимизатор запросов теперь решил использовать объединение слиянием Merge join, когда происходит сканирование индекса Index Scan.

Обратите внимание на различие между сканированием индекса и полным сканированием таблицы или последовательным сканированием: первое, которое также называется «сканированием таблицы», сканирует данные или страницы индекса, чтобы найти соответствующие записи, в то время как второе сканирует каждую строку таблицы.

Вы видите, что общее время выполнения уменьшилось и производительность должна быть лучше, но есть два сканирования индекса, что делает память здесь более важной, особенно если таблица не помещается в неё. В таких случаях сначала необходимо выполнить полное сканирование индекса, которое выполняется с помощью быстрого последовательного чтения и не представляет проблем, но затем у вас есть много случайных операций чтения для выборки строк по значению индекса. Это те случайные операции чтения, которые обычно на несколько порядков медленнее, чем последовательные. В этих случаях полное сканирование таблицы действительно происходит быстрее, чем полное сканирование индекса.

Совет: если вы хотите узнать больше о EXPLAIN или рассмотреть примеры более подробно, подумайте о прочтении книги Гийома Леларжа «Understanding Explain».

Time Complexity и Big O


Теперь, когда вы кратко рассмотрели план запроса, вы можете начать копать глубже и подумать о производительности в более формальных терминах с помощью теории сложности вычислений. Эта область теоретической информатики, которая, помимо прочего, фокусируется на классификации вычислительных задач в зависимости от их сложности; Эти вычислительные проблемы могут быть алгоритмами, но также и запросами.

Однако для запросов они не обязательно классифицируются в зависимости от их сложности, а скорее в зависимости от времени, необходимого для их выполнения и получения результатов. Это называется временной сложностью (time complexity), и чтобы сформулировать или измерить этот тип сложности, вы можете использовать обозначение big O.

С обозначением big O вы выражаете время выполнения с точки зрения того, насколько быстро оно растет относительно ввода, так как ввод становится произвольно большим. Большая нотация O исключает коэффициенты и члены более низкого порядка, поэтому вы можете сосредоточиться на важной части времени выполнения вашего запроса: скорости его роста. При выражении таким образом, отбрасывая коэффициенты и члены более низкого порядка, говорят, что временная сложность описывается асимптотически. Это означает, что размер ввода уходит в бесконечность.

На языке баз данных сложность определяет, сколько времени требуется для выполнения запроса по мере увеличения размера таблиц данных и, следовательно, базы данных.

Обратите внимание, что размер вашей базы данных увеличивается не только от увеличения объема данных в таблицах, но и факт наличия индексов также играет роль в размере.

Оценка сложности времени вашего плана запроса

Как вы видели ранее, план выполнения, среди прочего, определяет, какой алгоритм используется для каждой операции, что позволяет логически выражать каждое время выполнения запроса как функцию от размера таблицы, включенной в план запроса, который называют функцией сложности. Другими словами, вы можете использовать обозначение big O и план выполнения для оценки сложности запроса и производительности.

В следующих подразделах вы получите общее представление о четырех типах временных сложностей, и вы увидите некоторые примеры того, как сложность времени запросов может изменяться в зависимости от контекста, в котором она выполняется.

Подсказка: индексы — часть этой истории!

Однако следует отметить, что существуют различные типы индексов, различные планы выполнения и различные реализации для различных баз данных, поэтому перечисленные ниже временные сложности являются весьма общими и могут изменяться в зависимости от конкретных настроек.

O (1): Constant Time


Говорят, что алгоритм работает в постоянном времени (in constant time), если ему требуется одинаковое количество времени независимо от размера входных данных. Когда речь идет о запросе, он будет выполняться в постоянное время (in constant time), если требуется одинаковое количество времени независимо от размера таблицы.

Этот тип запросов на самом деле не распространен, но вот один из таких примеров: 

SELECT TOP 1 t.* 
FROM t


Сложность по времени постоянна, так как из таблицы выбирается одна произвольная строка. Следовательно, продолжительность времени не должна зависеть от размера таблицы.

Linear Time: O (n)


Говорят, что алгоритм работает в линейном времени, если время его выполнения прямо пропорционально размеру входных данных, то есть время линейно растет по мере увеличения размера входных данных. Для баз данных это означает, что время выполнения будет прямо пропорционально размеру таблицы: по мере роста числа строк в таблице растет время выполнения запроса.

Примером может служить запрос с условием WHERE для неиндексированного столбца: потребуется полное сканирование таблицы или Seq Scan, что приведет к временной сложности O (n). Это означает, что каждая строка должна быть прочитана, чтобы найти строку с нужным идентификатором (ID). У вас вообще нет ограничений, поэтому нужно считать каждую строку, даже если первая строка соответствует условию.

Рассмотрим также следующий пример запроса, который будет иметь сложность O (n), если на поле i_id нет индекса: 

SELECT i_id 
FROM item;


  • Предыдущее также означает, что другие запросы, такие как запросы на вычисление количества строк COUNT (*) FROM TABLE; будут иметь временную сложность O (n), так как потребуется полное сканирование таблицы, потому что общее количество строк не сохранено для таблицы. Иначе временная сложность была бы похожа на O (1).


С линейным временем выполнения тесно связано время выполнения планов, имеющих соединения таблиц. Вот несколько примеров:

  • Соединение хэшей (hash join) имеет ожидаемую сложность O (M+N).Классический алгоритм хеш-соединения для внутреннего объединения двух таблиц сначала подготавливает хеш-таблицу меньшей таблицы. Записи хеш-таблицы состоят из атрибута соединения и его строки. Доступ к хеш-таблице осуществляется путем применения хеш-функции к атрибуту соединения. Как только хеш-таблица построена, сканируется большая таблица, и соответствующие строки из меньшей таблицы находятся путем поиска в хеш-таблице.
  • Соединение слиянием (merge joins) обычно имеют сложность O (M+N), но оно будет сильно зависеть от индексов столбцов соединения и, в случае отсутствия индекса, от того, отсортированы ли строки в соответствии с ключами, используемыми в соединении:
    • Если обе таблицы отсортированы в соответствии с ключами, используемыми в соединении, то запрос будет иметь временную сложность O (M+N).
    • Если у обеих таблиц есть индекс для соединенных столбцов, то индекс уже поддерживает эти столбцы упорядочными и сортировка не требуется. Сложность будет O (M+N).
    • Если ни одна из таблиц не имеет индекса по соедиенным столбцам, сначала необходимо выполнить сортировку обеих таблиц, так что сложность будет выглядеть как O (M log M + N log N).
    • Если только одна из таблиц имеет индекс на соедиенных столбцах, то только та таблица, которая не имеет индекса, должна быть отсортирована, прежде чем произойдет этап соединения, так что сложность будет выглядеть как O (M + N log N).
  • Для вложенных соединений (nested joins) сложность обычно составляет O (MN). Это соединение эффективно, когда одна или обе таблицы чрезвычайно малы (например, меньше 10 записей), что является очень распространенной ситуацией при оценке запросов, поскольку некоторые подзапросы записываются для возврата только одной строки.


Помните: вложенное соединение (nested join) — это соединение, которое сравнивает каждую запись в одной таблице с каждой записью в другой.

Logarithmic Time: O (log (n))


Говорят, что алгоритм работает в логарифмическом времени, если его время выполнения пропорционально логарифму входного размера; Для запросов это означает, что они будут выполняться, если время выполнения пропорционально логарифму размера базы данных.

Эта логарифмическая сложность времени справедлива для планов запросов, где выполняется сканирование индекса Index Scan или сканирование кластеризованного индекса. Кластеризованный индекс — это индекс, где конечный уровень индекса содержит фактические строки таблицы. Кластеризованный индекс аналогичен любому другому индексу: он определен в одном или нескольких столбцах. Они образуют ключ индекса. Ключ кластеризации — это ключевые столбцы кластеризованного индекса. Сканирование кластеризованного индекса — это, в основном, операция чтения вашей СУБД для строки или строк сверху вниз в кластеризованном индексе.

Рассмотрим следующий пример запроса, где есть индекс для i_id и который обычно приводит к сложности O (log (n)): 

SELECT i_stock 
FROM item 
WHERE i_id = N;


Обратите внимание, что без индекса сложность времени была бы O (n).

Quadratic Time: O (n^2)


Считается, что алгоритм выполняется за квадратичное время, если время его выполнения пропорционально квадрату входного размера. Опять же, для баз данных это означает, что время выполнения запроса пропорционально квадрату размера базы данных.

Возможным примером запроса с квадратичной временной сложностью является следующий: 

SELECT * 
FROM item, author 
WHERE item.i_a_id=author.a_id


Минимальная сложность может быть O (n log (n)), но максимальная сложность может быть O (n^2), основанная на информации индекса атрибутов соединения.

Подводя итоги, вы также можете взглянуть на следующую шпаргалку, чтобы оценить производительность запросов в зависимости от их временной сложности и их эффективности:

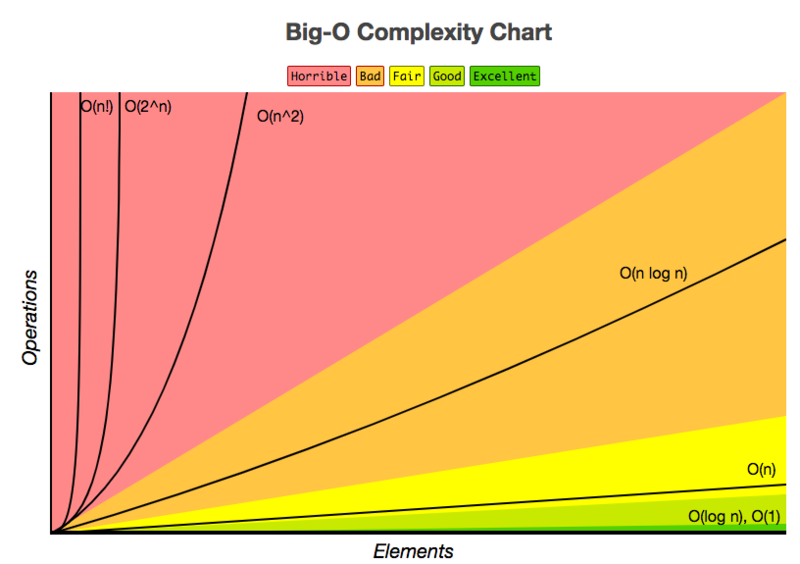
dkcqfhsmh_fxl7gorardyts9ptu.png


SQL Tuning


Учитывая план выполнения запроса и сложность времени, вы можете дополнительно настроить свой запрос SQL. Вы можете начать с уделения особого внимания следующим моментам:

  • Замените ненужное полное сканирование больших таблиц (full table scans) сканированием индексов (index scans);
  • Убедитесь, что применяется оптимальный порядок соединения таблиц.
  • Убедитесь, что индексы используются оптимально. И
  • Используется кэширование полнотекстовых сканирований малых таблиц (cache small-table full table scans.).


Дальнейшее использование SQL


Поздравляю! Вы дошли до конца этой статьи, которая только что дала вам небольшой взгляд на производительность SQL-запросов. Я надеюсь, что вы получили больше информации об антипаттернах, оптимизаторе запросов и инструментах, которые вы можете использовать для анализа, оценки и интерпретации сложности вашего плана запросов. Однако вам еще столько всего предстоит открыть! Если вы хотите узнать больше, почитайте книгу «Database Management Systems» авторства R. Ramakrishnan и J. Gehrke.

Наконец, я не хочу отказывать вам в этой цитате от пользователя StackOverflow:

Мой любимый антипаттерн не проверяет ваши запросы.

Однако он применим, когда:

  • Ваш запрос предусматривает более одной таблицы.
  • Вы считаете, что у вас оптимальный дизайн для запроса, но не пытайтесь проверить свои предположения.
  • Вы принимаете первый работающий запрос, не зная, насколько он близок к оптимальному.

© Habrahabr.ru