[Перевод] Вычисления с плавающей запятой: сравниваем вывод в разных языках

С вашим языком программирования все в порядке — он просто производит вычисления с плавающей запятой. Изначально компьютеры могут хранить только целые числа, так что им нужен какой-то способ представления десятичных чисел. Это представление не совсем точное. Именно поэтому, чаще всего, 0.1 + 0.2!= 0.3.
ИТ-эксперт Эрик Уиффин, директор по инжинирингу компании Devetry, провел любопытный эксперимент: сравнил вывод в разных языках программирования при вычислениях с плавающей запятой. В рамках опыта автор продемонстрировал специфику выполнения одной и той же математической операции в нескольких десятках языков.
Предлагаем хабрасообществу наш перевод этой статьи. Обращаем ваше внимание, что позиция автора не всегда может совпадать с мнением МойОфис.
Если вы используете стандартную десятичную систему счисления, то несократимая обыкновенная дробь представляется конечной десятичной дробью только в том случае, когда ее знаменатель содержит в разложении на простые множители только числа 2 и 5 (т.е. только простые делители числа 10). Таким образом, ½, ¼, 1/5, 1/8 и 1/10 могут быть точно выражены, поскольку все знаменатели используют простые множители числа 10. Напротив, ⅓, 1/6, 1/7 и 1/9 — периодические десятичные дроби, потому что в их знаменателях используется простой множитель 3 или 7.
В двоичном формате (или с основанием 2) единственным простым делителем является 2, поэтому вы можете точно выразить только те дроби, знаменатель которых имеет 2 в качестве простого делителя. В двоичном формате ½, ¼, 1/8 будут точно выражены в виде десятичных дробей, а 1/5 или 1/10 будут периодическими десятичными дробями. Таким образом, 0,1 и 0,2 (1/10 и 1/5), будучи чистыми десятичными числами в десятичной системе, являются периодическими десятичными числами в системе с основанием 2, которую использует компьютер. Если вы выполняете вычисления с их участием, вы получаете остатки, которые переносятся, когда вы конвертируете «компьютерное» число с основанием 2 (двоичное) в более удобочитаемое представление с основанием 10.
Ниже приведены несколько примеров печати .1 + .2 в стандартный вывод на разных языках. Все примеры представлены в формате «Язык — Код — Результат».
PowerShell по умолчанию использует тип double, но поскольку он работает на .NET, то имеет те же типы, что и C#. Благодаря этому можно напрямую использоватьтип Decimal[decimal], указав имя типа либо посредством суффикса d.
Подробнее об этом читайте ниже, в разделе про C#.

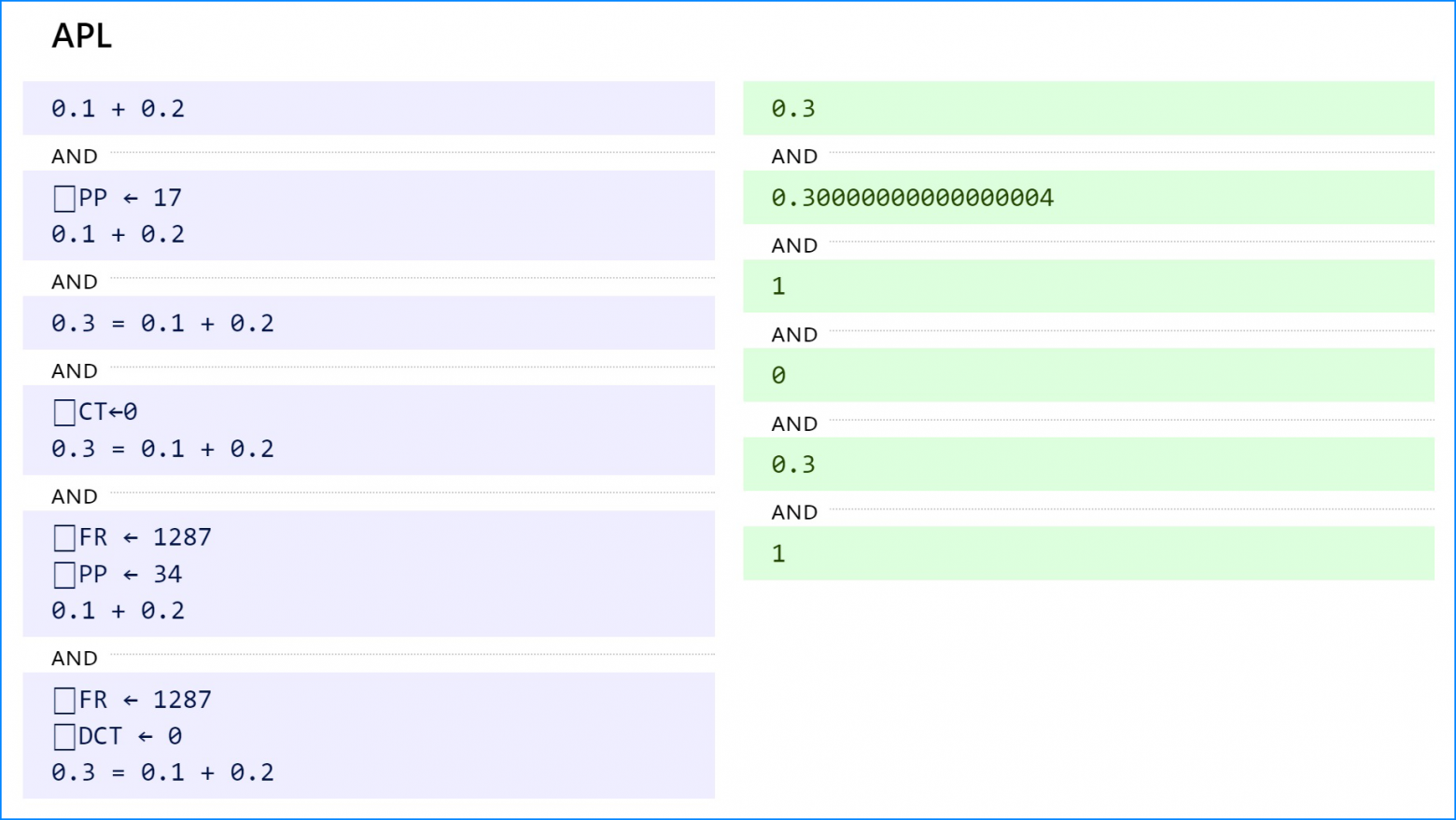
По умолчанию точность вывода APL — 10 значимых цифр. Установка значения 17 для ⎕PP выдает ошибку, однако все еще верно (1), что 0.3 = 0.1 + 0.2, поскольку допуск сравнения по умолчанию составляет около 10^-14 . Установка ⎕CT на 0 выдает неравенство. Dyalog APL также поддерживает 128-битные десятичные числа (активируется установкой представления с плавающей запятой, ⎕FR, на 1287, т. е. 128-битным десятичным числом), где даже установка допусков десятичного сравнения (⎕DCT) на ноль все еще делает уравнение верным. Убедитесь в этом здесь! В NARS2000 доступны числа с плавающей точкой с множественной точностью, рациональные числа с неограниченной точностью и комплексные интервальные вычисления с кругами (ball arithmetic).




C# поддерживает 128-битные десятичные числа с точностью до 28–29 значащих цифр. Однако их диапазон меньше, чем у типов с плавающей запятой одинарной и двойной точности. Десятичные литералы обозначаются суффиксом m.


Clojure поддерживает произвольную точность и соотношения. (+ 0,1M 0,2M) возвращает 0,3M, в то время как (+ 1/10 2/10) возвращает 3/10.


Спецификация CL на самом деле не требует даже чисел с основанием 2 с плавающей запятой (не говоря уже о 32-битных одинарных и 64-битных двойных), но все высокопроизводительные реализации, похоже, используют числа с плавающей запятой IEEE с обычными размерами. Это было протестировано, в частности, на SBCL и ECL.







Elvish использует тип double языка Go для числовых операций.


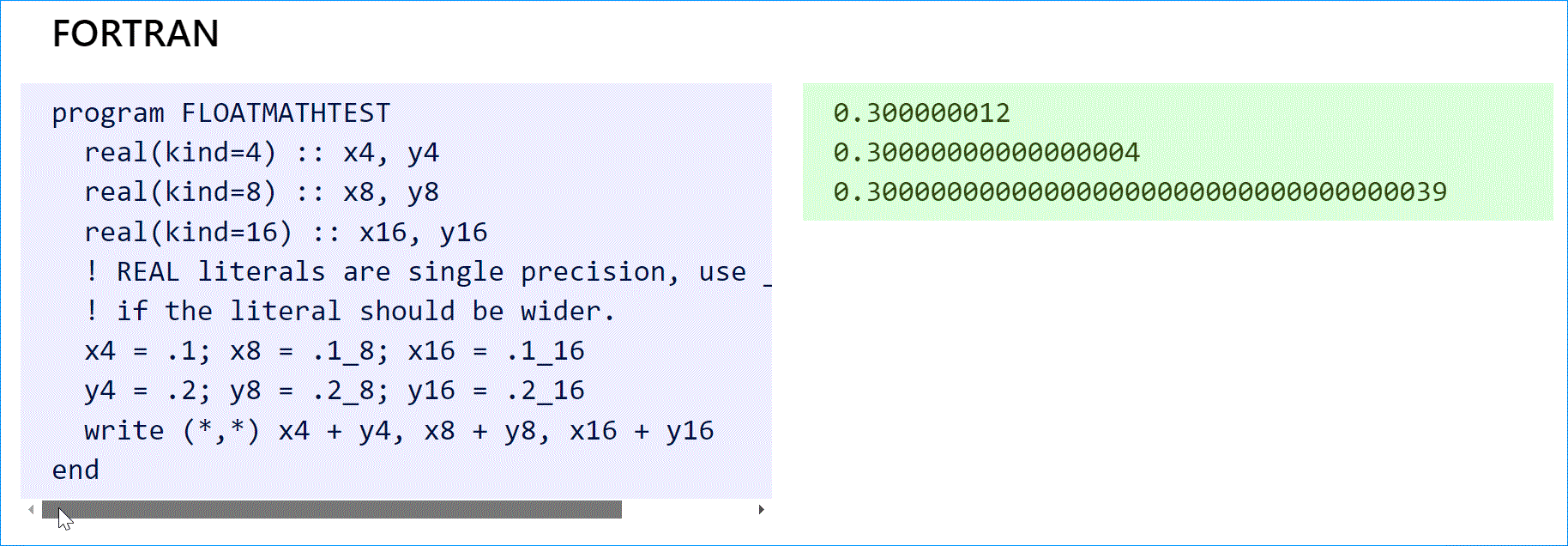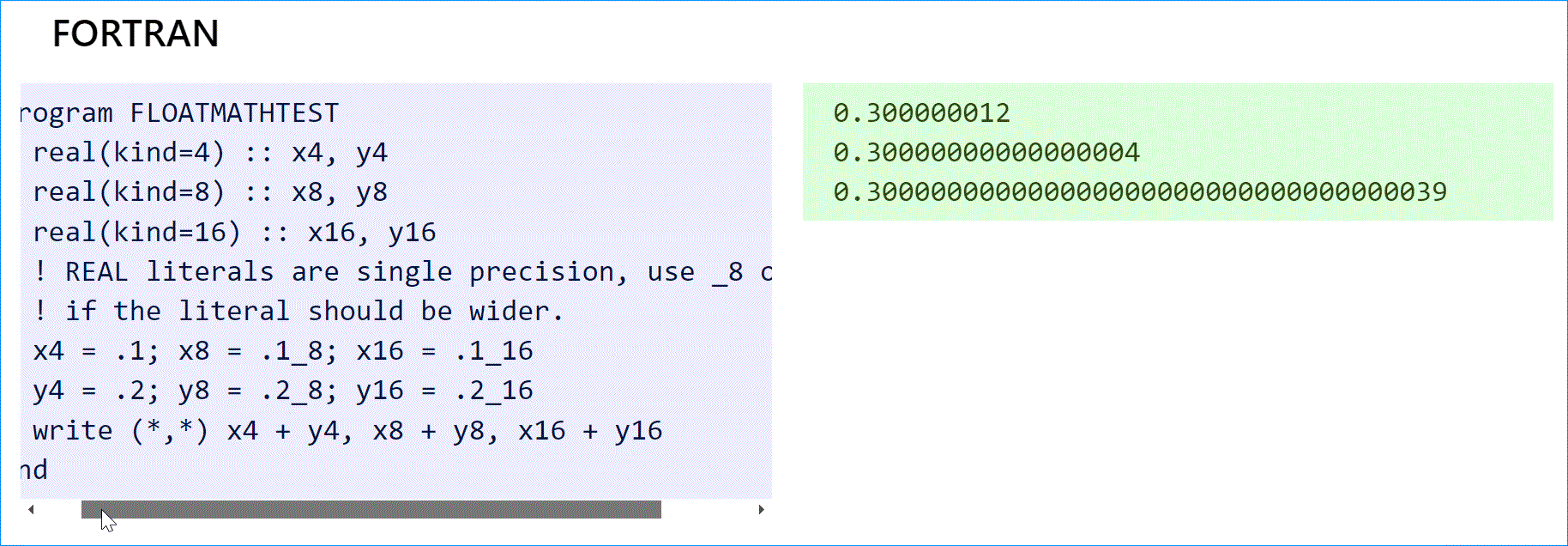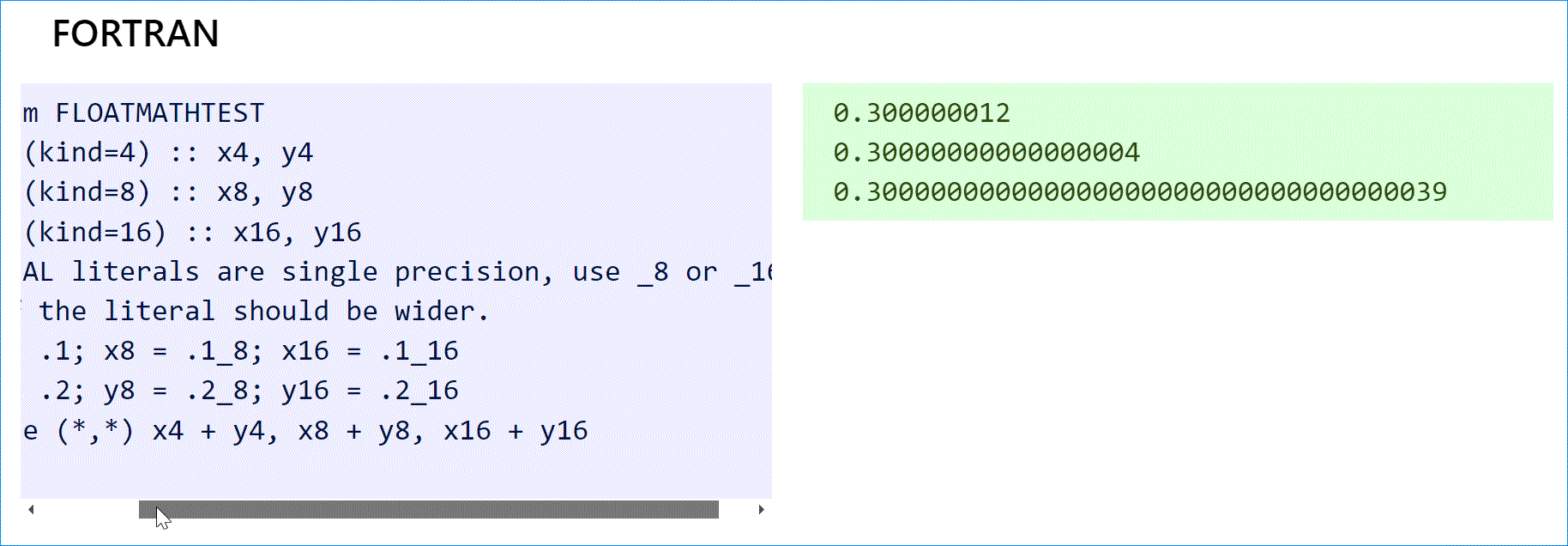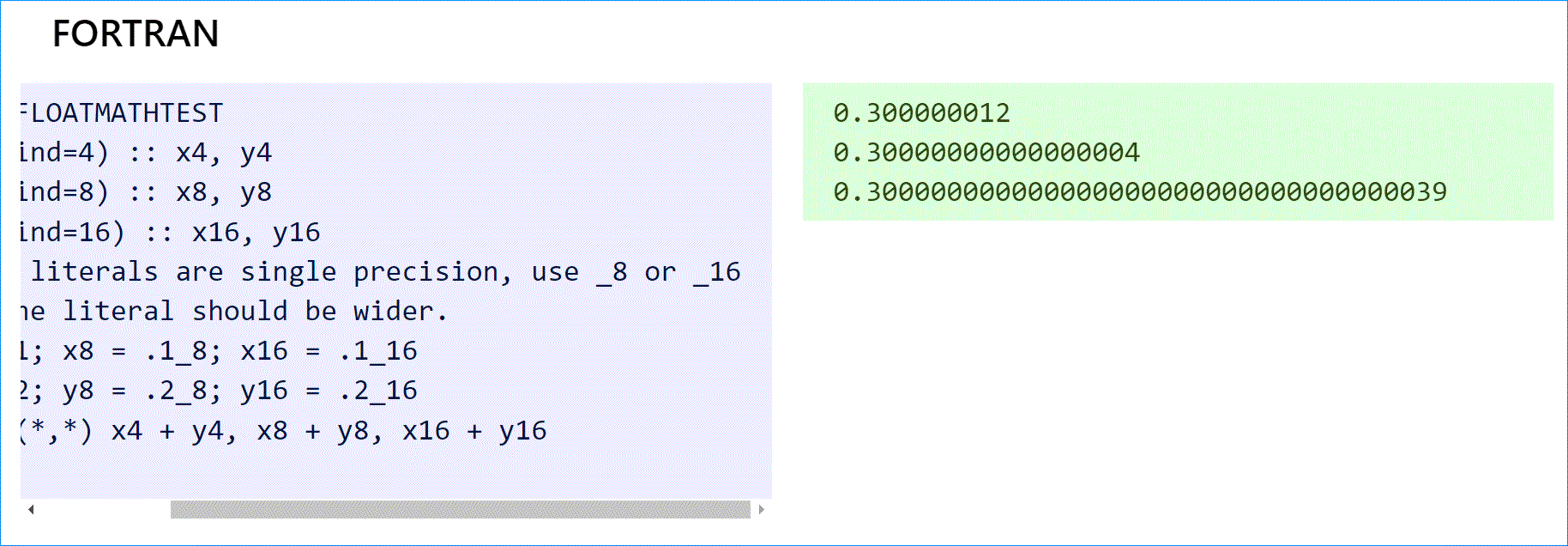


Если вам нужны действительные числа, пакеты типа exact-real дадут вам правильный ответ.
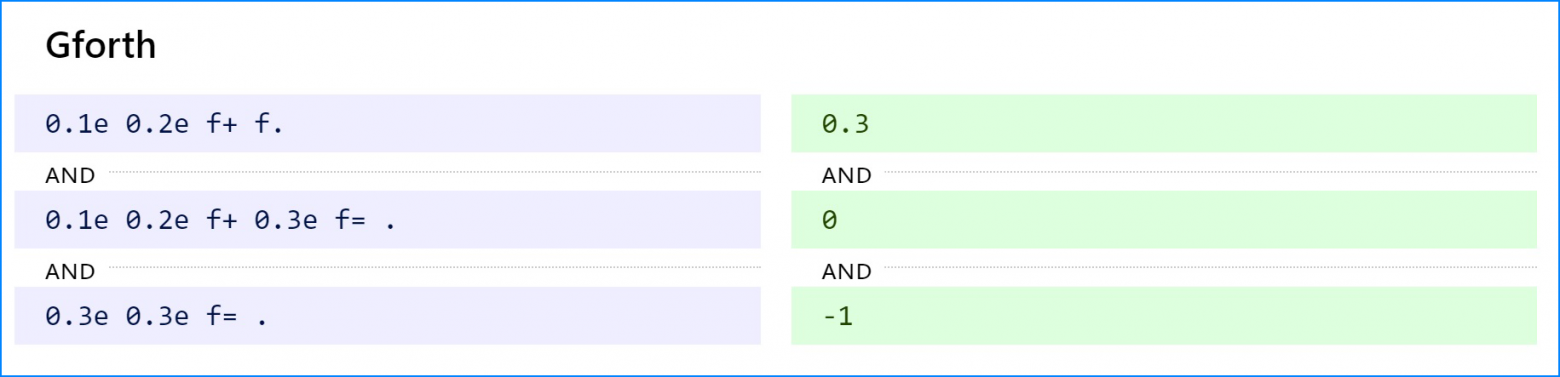
В Gforth 0 означает ложь, а -1 означает истину. Первый пример выводит 0,3, но этот результат не равен фактическому значению 0,3.

Числовые константы Go имеют произвольную точность.

Буквенные десятичные значения в Groovy являются экземплярами java.math.BigDecimal.




Java имеет встроенную поддержку чисел произвольной точности с использованием класса BigDecimal.

Библиотека decimal.js предоставляет тип Decimal произвольной точности для JavaScript.

Julia имеет встроенную поддержку рациональных чисел, а также встроенный тип данных BigFloat произвольной точности.


См. справочную документацию.



Спецификация схемы содержит понятие точности.

В языке Mathematica есть довольно продуманный внутренний механизм для работы с числовой точностью, и она поддерживает произвольную точность.
По умолчанию для исходных данных 0,1 и 0,2 в этом примере используется MachinePresicion. При обычном значении MachinePrecision в 15,9546 цифр, 0,1 + 0,2 фактически имеет [FullForm][4] 0,300000000000000004, но выводится как 0,3.
Mathematica поддерживает рациональные числа: 1/10 + 2/10 равно 3/10 (что имеет FullForm Rational[3, 10]).





PHP echo преобразует 0.300000000000000004441 в строку и сокращает ее до »0.3». Чтобы добиться желаемого результата с плавающей запятой, отрегулируйте параметр точности: ini_set("precision", 17).

Добавление примитивов с плавающей запятой только кажется верным для вывода, потому что не все 17 цифр выводятся по умолчанию. Базовый пакет Math: BigFloat позволяет выполнять операции с плавающей запятой с произвольной точностью, никогда не используя числовые примитивы.

Вам нужно загрузить файл «frac.min.l».

PostgreSQL рассматривает десятичные литералы как числа произвольной точности с фиксированной точкой. Для получения чисел с плавающей запятой требуется явное приведение типов.
PostgreSQL 11 и более ранние версии выдает результат 0.3 для запроса SELECT 0.1::float + 0.2::float;, но результат округляется только для отображения, под капотом же у нас все еще 0.300000000000000004.
В PostgreSQL 12 поведение по умолчанию для текстового вывода чисел с плавающей запятой было изменено с более удобочитаемого округленного формата на максимально точный формат. Формат можно настроить с помощью параметра конфигурации extra_float_digits.


Pyret имеет встроенную поддержку как рациональных чисел, так и чисел с плавающей запятой. Числа, написанные как обычно, считаются точными. Напротив, RoughNums представлены плавающими точками и написаны с префиксом ~, что указывает на то, что они не являются точными результатами. Пользователь, увидевший результат вычислений ~0,30000000000000004, знает, что к этому значению нужно относиться скептически. RoughNums нельзя прямо сравнивать для равенства; их можно сравнивать только с заданным допуском.
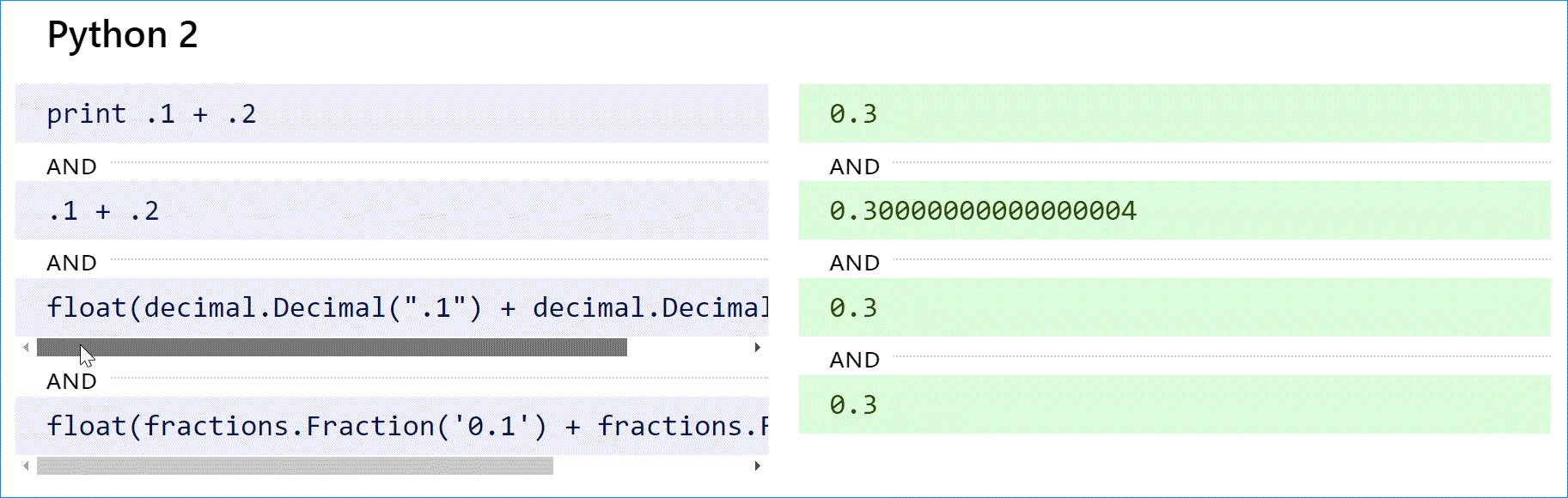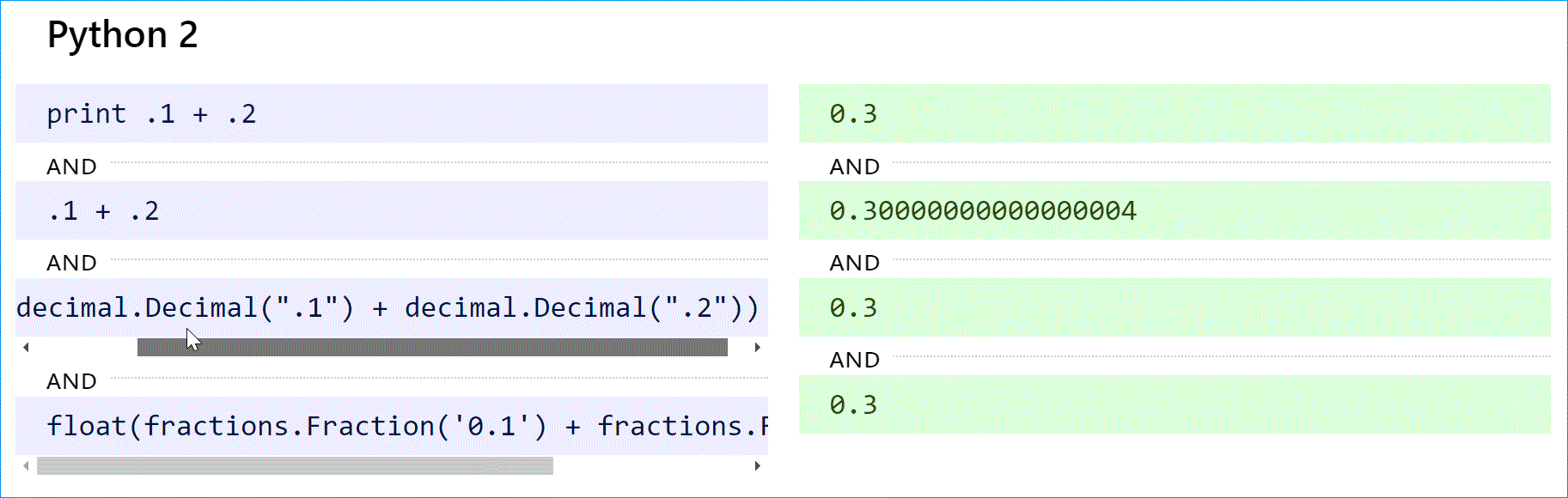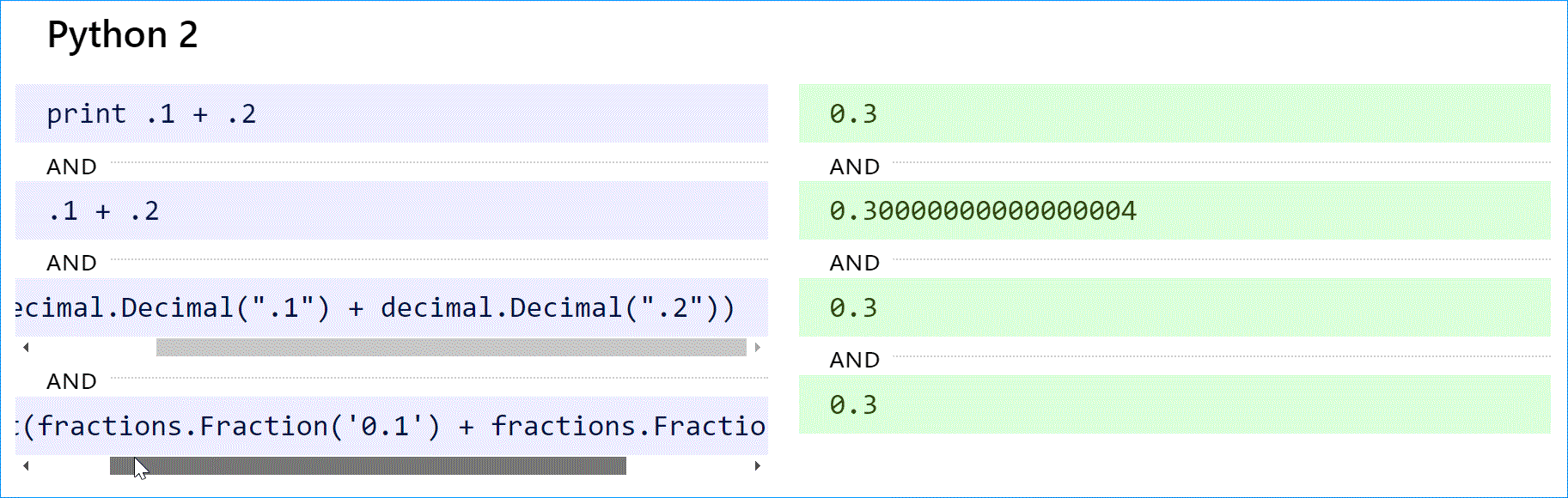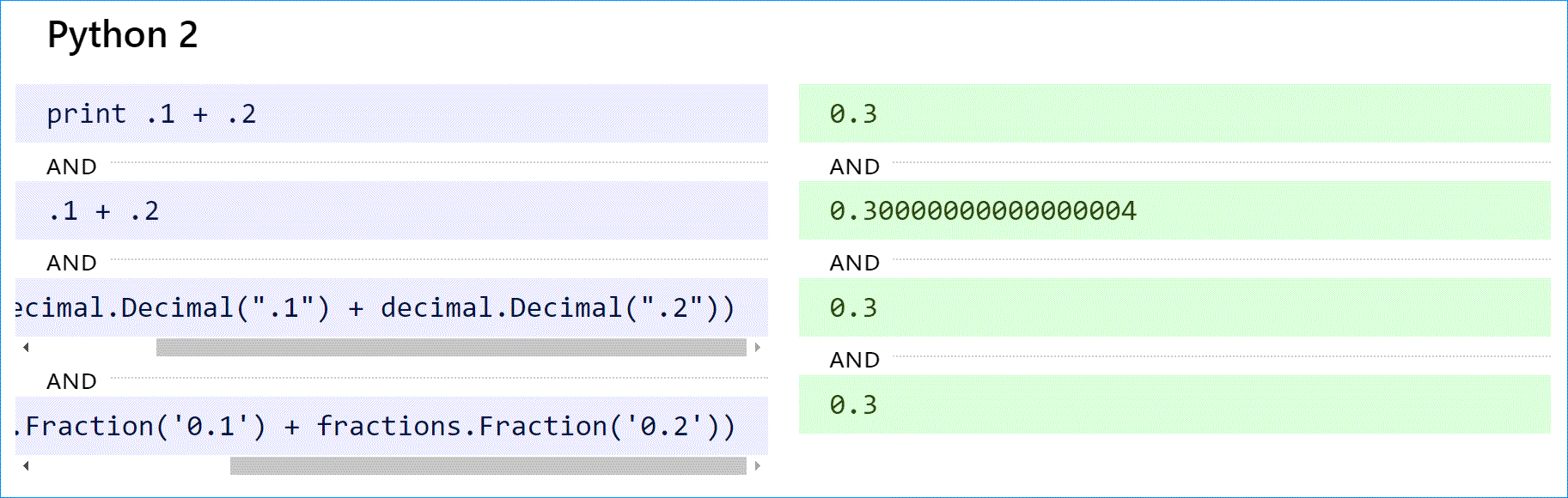
В Python 2 оператор print преобразует 0,300000000000000004 в строку и сокращает ее до »0,3». Чтобы добиться желаемого результата с плавающей запятой, используйте print repr(.1 + .2). Это было исправлено в Python 3 (см. ниже).
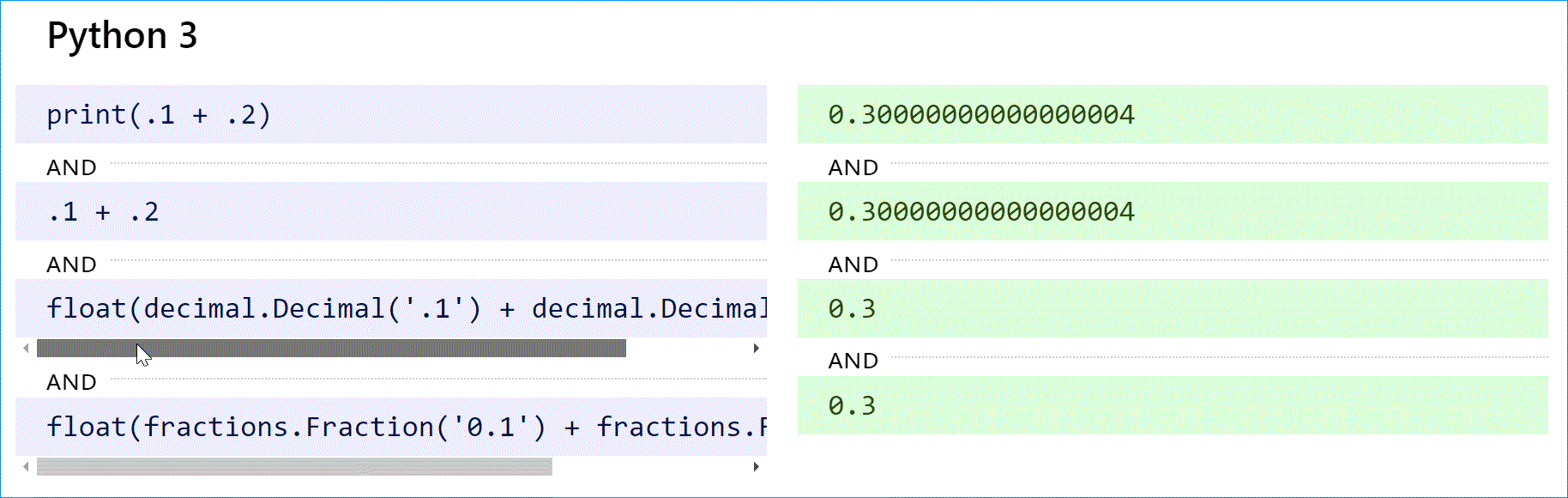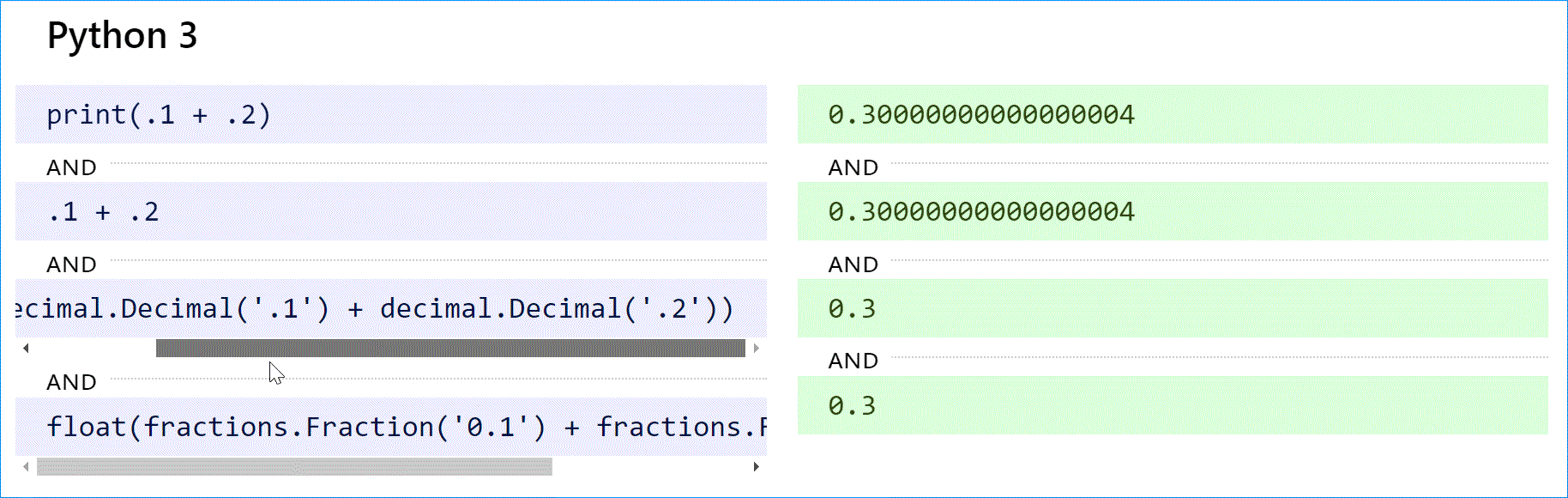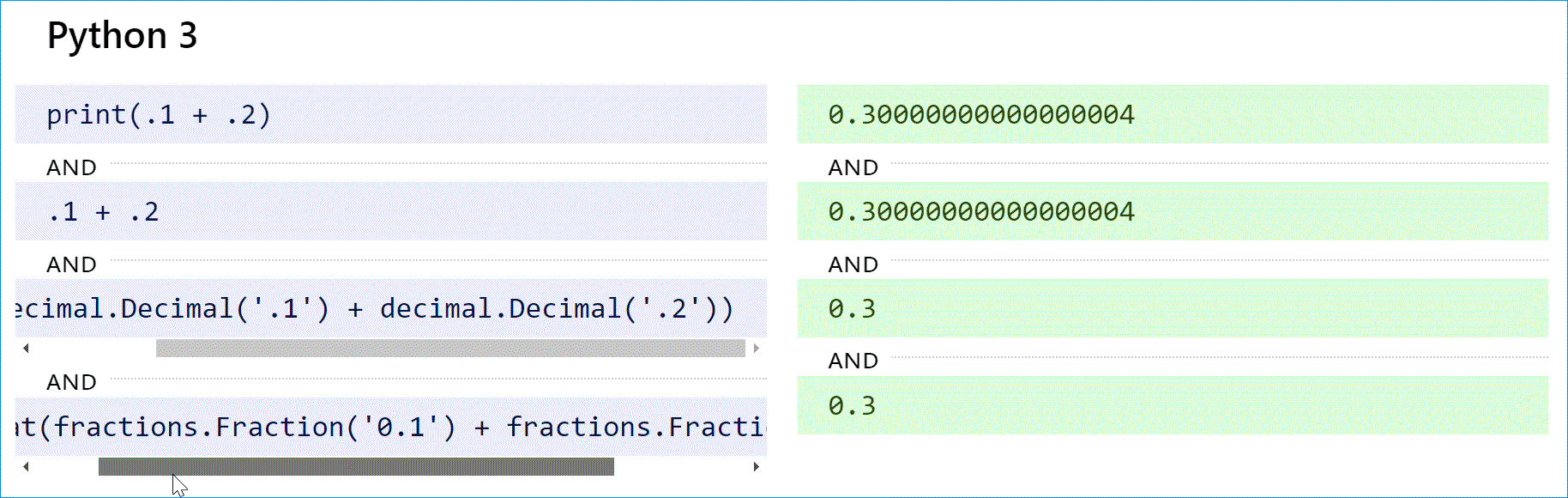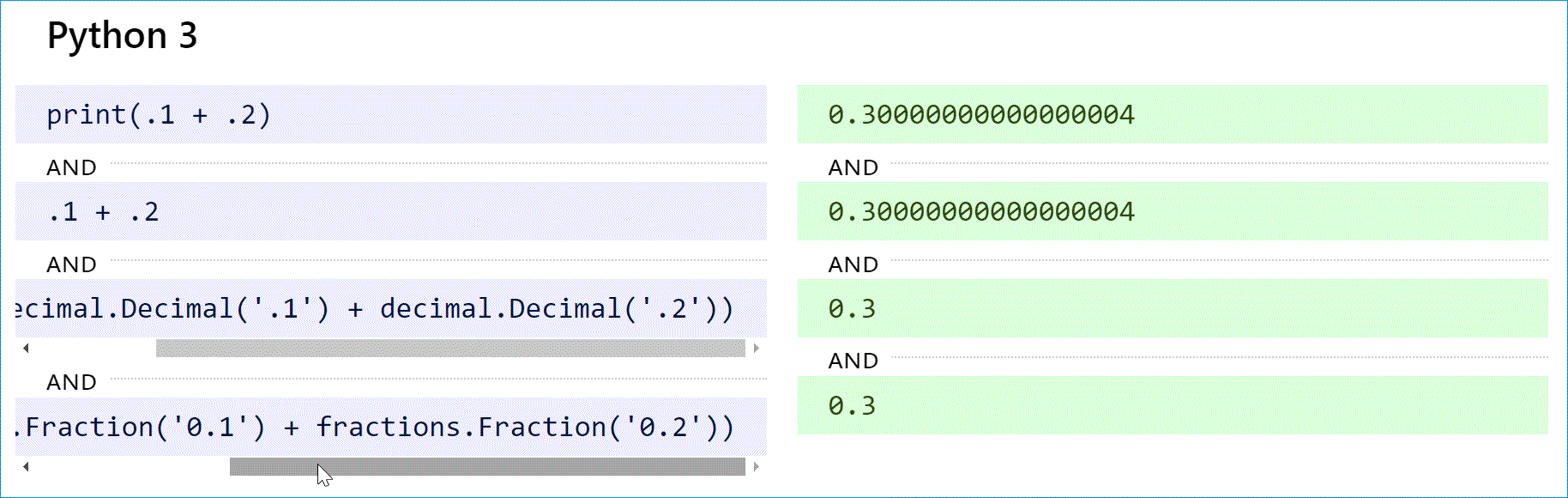
Python (как 2, так и 3) поддерживает десятичные вычисления с модулем decimal и истинные рациональные числа с модулем дробей.



Raku по умолчанию использует рациональные числа, поэтому .1 хранится примерно так: { numerator => 1, denominator => 10 }. Чтобы в реальности вызвать такое поведение, вы должны заставить числа иметь тип Num (double в терминах C) и использовать базовую функцию вместо функций sprintf или fmt (поскольку в этих функциях есть ошибка, которая ограничивает точность вывода).


Ruby напрямую поддерживает рациональные числа в синтаксисе версии 2.1 и новее. Для более старых версий используйте Rational. В Ruby также есть библиотека для работы с десятичными знаками: BigDecimal.
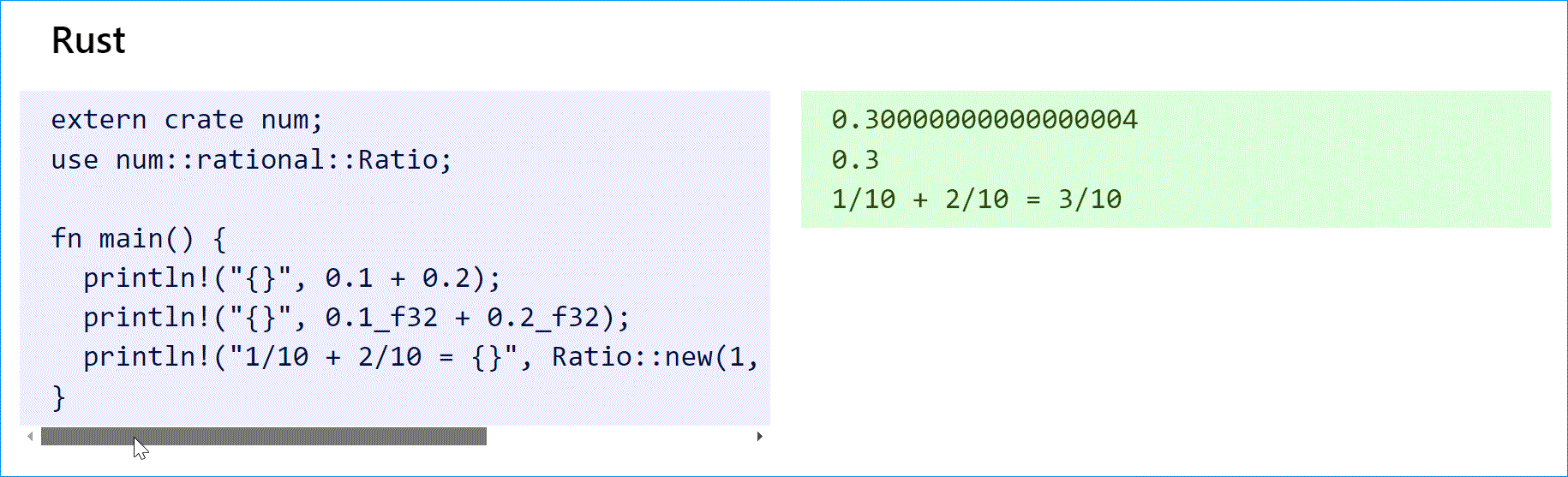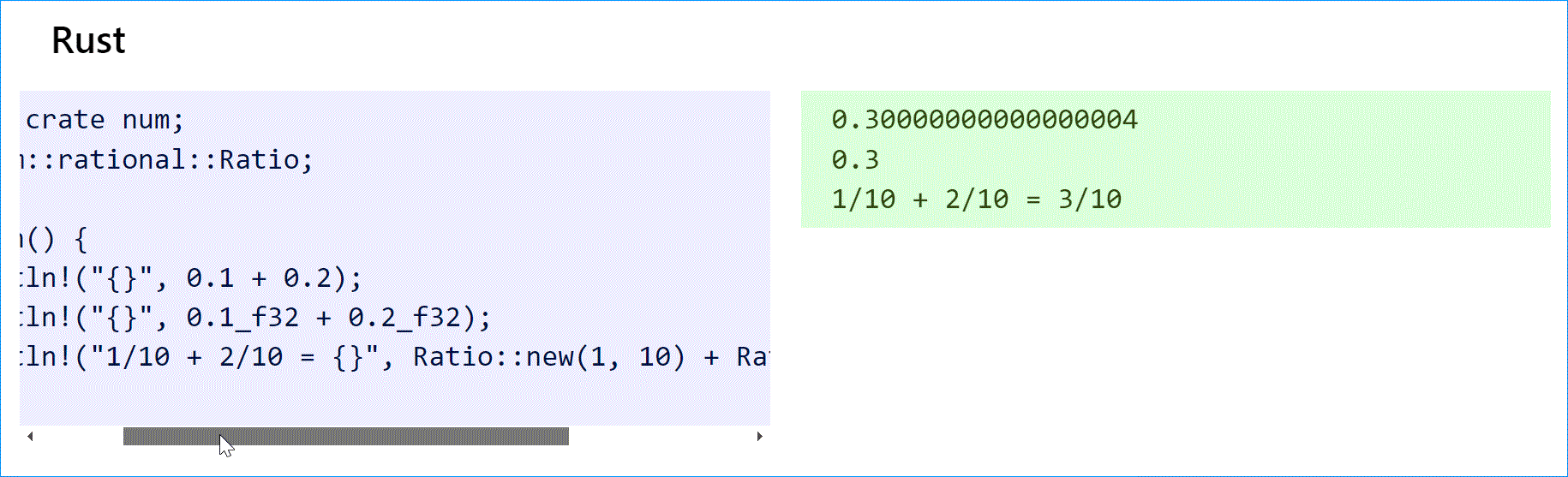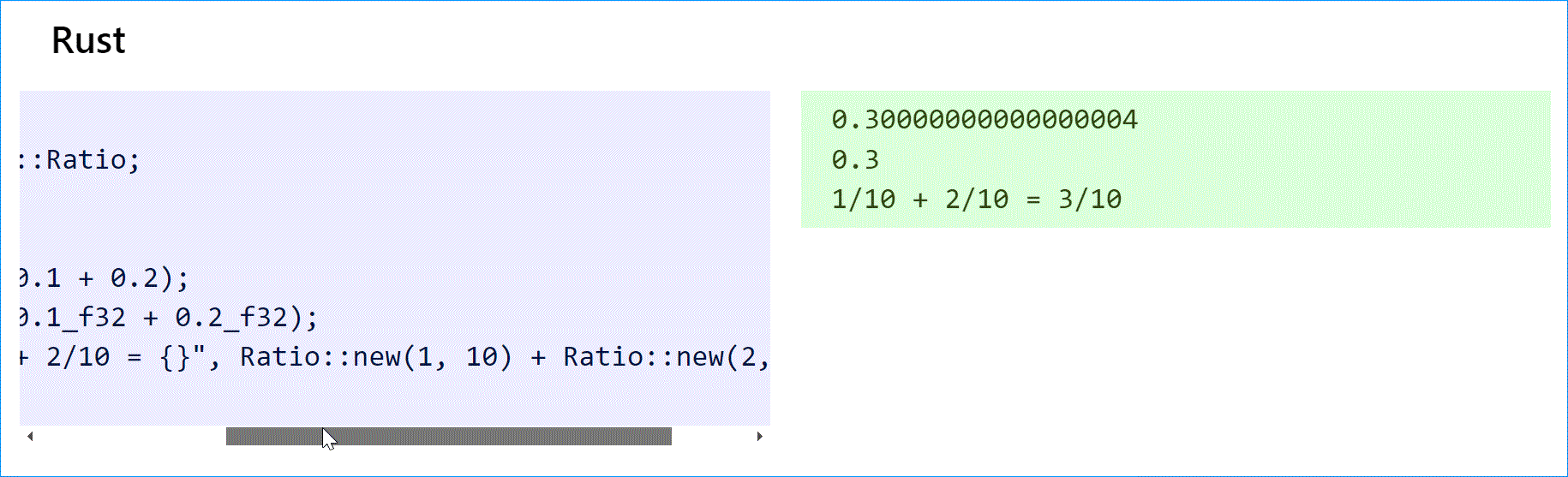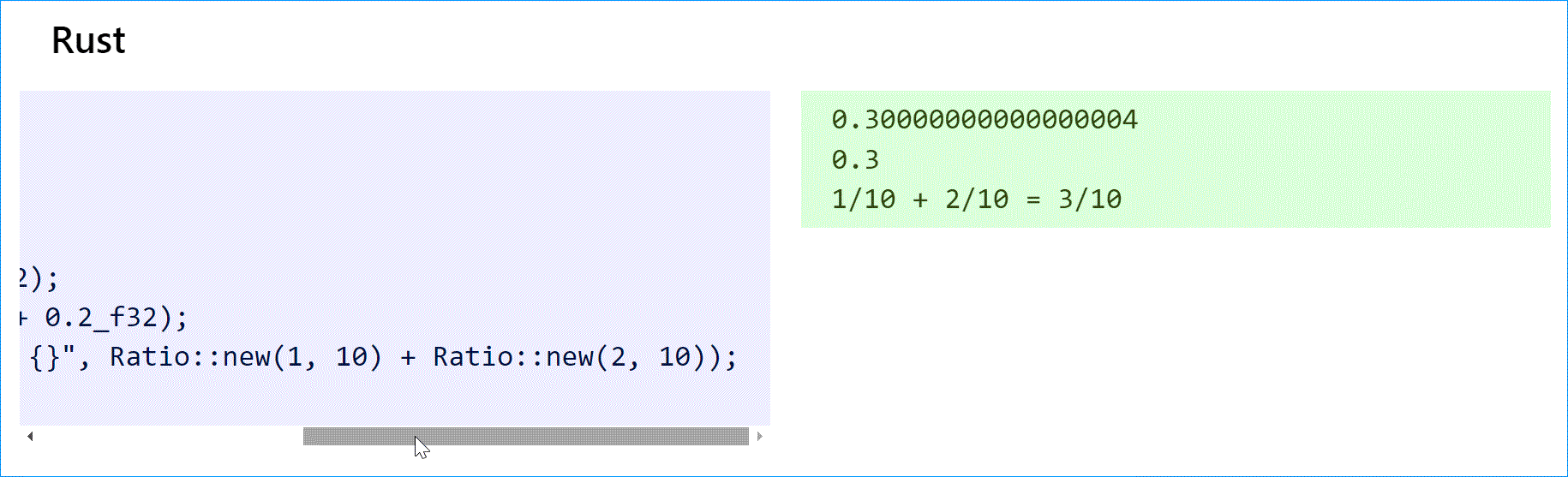
В Rust есть поддержка рациональных чисел из num crate.

SageMath поддерживает различные поля для вычислений: вещественные числа произвольной точности, RealDoubleField, Ball Arichmetic, рациональные числа и т. д.


В большинстве операций Smalltalk по умолчанию использует дроби; на самом деле стандартное деление приводит к дробям, а не к числам с плавающей запятой. Squeak и аналогичные Smalltalk предоставляют «масштабированные десятичные числа», которые позволяют использовать вещественные числа с фиксированной точкой (s-суффикс указывает точные разряды).

Swift поддерживает десятичные вычисления с модулем Foundation.




Добавление символа типа идентификатора # к любому идентификатору приводит к тому, что он становится Double.
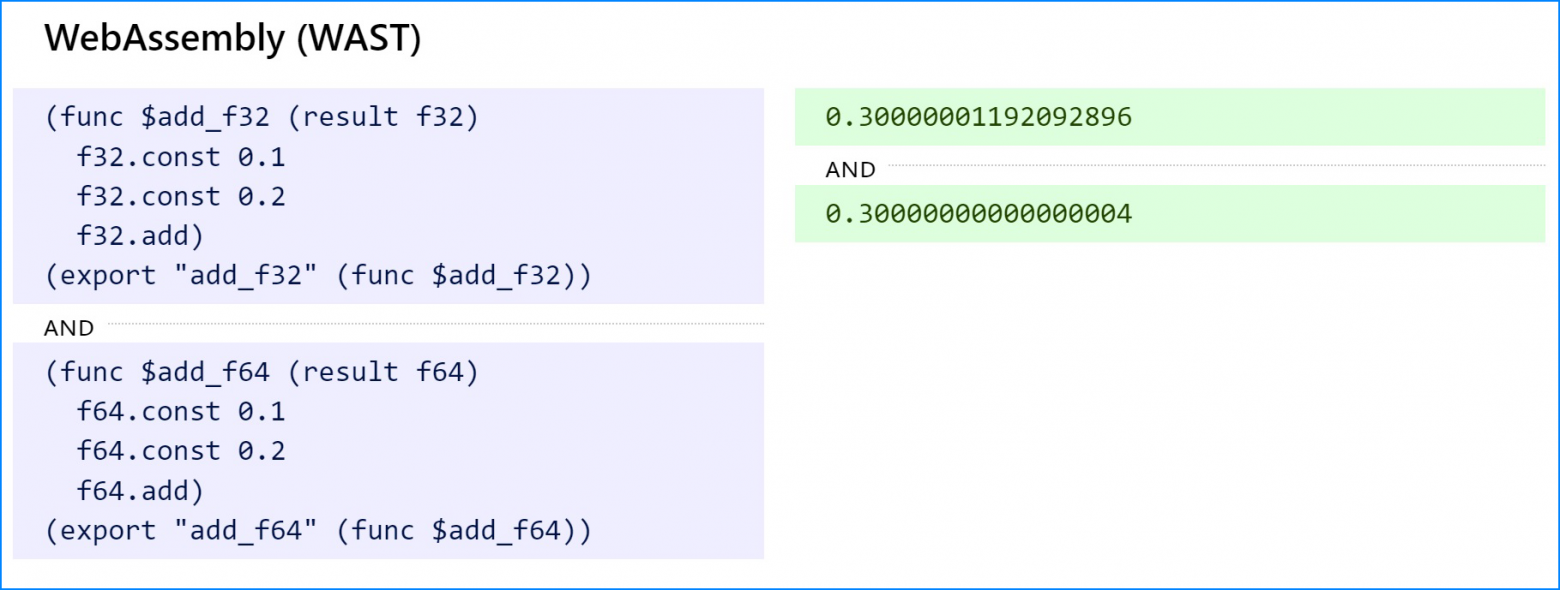
Смотрите демо.




***
Будем рады узнать в комментариях ваше мнение об описанном опыте с вычислениями и его результатах. Впереди — еще больше полезных переводов и материалов с ИТ-экспертизой от специалистов МойОфис. Следите за нашими новостями и блогом на Хабре!
