[Перевод] Технология создания динамических моделей на примере обогрева помещения24.08.2022 10:01

Данная учебная задача показывает, как создать динамическую модель системы, используя технологии струкутрного моделирования. Модель содержит в себе нагреватель (объект управления), управляемый термостатом (система управления), и обогреваемую комнату (модель окружения), в которой необходимо поддерживать заданную температуру.

Несмотря на то, что данная модель очень проста, процесс ее создания, а также необходимая последовательность шагов и выполняемые действия в данной статье такие же, как для моделей сложных систем.

Исследуемая система

У нас есть помещение, обгорев которого осуществляется системой кондиционирования воздуха: часть воздуха забирается в нагреватель, где нагревается и возвращается обратно в помещение.

Процесс создания модели

Создание любых математических моделей начинается с определения целей математического моделирования. Цель определяет средства!

Процесс создания любых моделей можно разделить на две стадии, подготовительная стадия и стадия создания модели.

По моему мнению первая стадия более важная, чем вторая.

Подготовительная стадия. Данная стадия осуществляется вне среды моделирования и включает следующие шаги:

Определение цели моделирования и требований к модели.
Разработка структуры модели.
Определение упрощения и приближения физической модели и формирование математических уравнений.
Сбор данных по параметрам модели, если возможно собрать реальные данные измерения для валидации результата моделирования.
Стадия создания модели. Эта стадия разработки модели непосредственно в среде моделирования, после того как подготовительная работа выполнена. Стадия включает следующие шаги:
Создание и отладка модели, компонентов модели.
Интеграция компонентов в комплексную модель и ее отладка.
При наличии возможности сравнение с реальными данными (валидация модели).
Корректировка модели по экспериментальным данным.
Если модель не отвечает поставленным целям, то возврат на пункт 1, 2 или 3.

Рассмотрим все вышеперечисленные стадии создания модели на примере системы обогрева дома.

1. Цели моделирования

Прежде чем создавать структуру модели, рассмотрим возможные цели и требования к модели. В случае модели системы обогрева дома это могут быть:

Оценка влияния изменения внешней температуры на температуру в доме.
Оценка расхода энергии в зависимости от температуры в доме и внешней температуры среды.
Оценка скорости нагрева и охлаждения дома при включении/отключении системы обогрева.
Настройка регулятора температуры.

Далее покажем, как цели моделирования определяют нашу модель.

2. Структура модели

После определения целей моделирования мы можем сформировать структуру будущей модели, которая должна содержать следующие физические компоненты:

Внутренние помещение в доме
Нагреватель
Контроллер температуры
Внешняя среда

Целью моделирования является расчёт температуры. Мы должны для данных физических элементов получить характеристики, необходимые для термического расчёта. Например, для помещения нам не нужны такие характеристики как цвет потолка и пола, а для нагревателя нас не интересует его масса. Для решения задачи мы должны получить набор термических характеристик компонентов модели.

Контроллер температуры получает температуру в помещении и включает нагреватель, если температура ниже заданного значения.

Структура модели представлена на рисунке 1

Рисунок 1. Структура модели обогрева дома

3. Принятые допущения модели и математические уравнения

На этом этапе нам необходимо определить, насколько точно мы будем моделировать наш объект. Необходимая точность модели задается целями моделирования и определяется набором допущений упрощений в физическом описании исследуемого процесса. Помещение можно моделировать с помощью 3D моделирования на супер ЭВМ, где комната представленном миллионом элементарных объемов в каждом из которых считается температура и усчитывается потоки воздуха от конвенции. Так же может учитываться нагрев помещения излучением через окна или учет тепловыделения от человека.

Например, если бы в целях моделирования, было определение распределения воздуха по помещению и определения зоны перегрева и охлаждения для выбора мест для оборудования, то необходим 3D расчет. Как на рисунке 2.

Рисунок 2. Пример визуализации 3D расчета помещения.

Такой расчет тоже имеет право на существования, но занимает часы, дни и недели. Нам же нужно более быстрый результат поэтому упрощаем задачу.

Допущения

Принимаем следующие допущения:

расход воздуха M_heater_air (кг/час) через нагреватель постоянный;
температура нагреваемого воздуха T_heater после нагревателя постоянная (нагреватель обладает достаточной мощностью и встроенной системой управления для поддержания температуры нагреваемого воздуха);
контроллер работает в режиме термостата, может только включать и выключать нагреватель;
зависимостью свойства воздуха (плотность, теплоемкость c_air = const) от температуры пренебрегаем;
mассу m_room воздуха в помещении считаем постоянной.

Математические уравнения модели

Обратите внимание на последовательность, математические уравнения появляются только после того, как, мы сформировали допущения и упрощения для нашей задачи. Принимая объемы воздуха, расходы и другие величины постоянными, мы сокращаем количество динамических уравнений в общей системе.

Для комнаты изменение температура определяется разностью потока тепла, полученного с горячим воздухом, и тепловыми потерями.

Уравнения изменения температуры в помещении:

$\frac{dT_{room}}{dt}=\frac{1}{m_{room}\cdot c_{air}}\left[\frac{dQ_{gain}}{dt}-\frac{dQ_{loss}}{dt}\right] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(1)}$

где:
$m_{room}$ — масса воздуха в комнате [кг];
$c_{air}$ — теплоемкость воздуха [Дж/(кг $\cdot$ К)];

$\frac{dQ_{gain}}{dt}$ — поток тепла в помещении в единицу времени (мощность теплового потока в помещение) [Дж/сек] или [Дж/час];

$\frac{dQ_{loss}}{dt}$ — поток тепла в единицу времени [Дж/сек] или [Дж/час].

Поскольку мы приняли в допущениях, что температура горячего воздуха на выходе из обогревателя постоянная и расход подогреваемого воздуха также постоянный, то в этом случае тепло, поступающее в комнату, определяется разностью температуры холодного и нагретого воздуха.

Уравнения для мощности теплового потока в помещении:

$\frac{dQ_{gain}}{dt}=M_{heater-air}\cdot c_{air}(T_{heater}-T_{room}) \ \ \ \ \ \ \ \ \ \mathbf{(2)}$

где:
$M_{hater-air}$ — расход воздуха через обогреватель [кг/с] или [кг/час];
$T_{heater}$ — температура воздуха после нагревателя;
$T_{room}$ — температура помещения.

Мощность тепловых потерь в окружающую среду определяется разностью температуры внутри помещения и снаружи и термическим сопротивлением

Уравнения для мощности тепловых потерь в окружающую среду:

$\frac{dQ_{loss}}{dt}=k\cdot A \cdot\frac{T_{room}-T_{outside}}{D}=\frac{T_{room}-T_{outside}}{R} \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3)}$

где:
— коэффициент теплопроводности материала [Дж/(м $\cdot$ c $\cdot$ К)] или [Дж/(м $\cdot$ ч. $\cdot$ К)],
— площадь теплообмена [м²],
— толщина стенки [м],
$R = \frac{D}{k\cdot A}$ — термическое сопротивление [с $\cdot$ К /Дж].

4. Сбор исходных данных для моделирования

Только после того, как уравнения сформированы, у нас появляются требования к исходным данным, по задаче. Исходные данными становится только величины, используемые в уравнениях. Например, в задаче не нужна вязкость воздуха. А если бы мы считали в 3D, то вязкость воздуха и ее зависимость от температуры были бы в исходных данных. Чем сложнее используемые уравнения, тем больше исходных данных нам необходимо.

Таблица 1. Исходные данны для модели

Обозначение	Описание формулы и значение	Единицы измерения
A	Площадь стен и окон: Awall = 914 Awindow = 6	м²
D	Толщина стен и окон: Dwall = 0,2 Dwindow = 0,01	м
mair	Масса воздуха в комнате Mair =1470	кг
k	Теплопроводность материала стен и окон: kwall = 136.8 kwindow = 2808	Дж/(м $\cdot$ ч. $\cdot$ К)
R	Термическое сопротивление $R=\frac{D}{k \cdot A}$ $R_{wall}=1.599\cdot10^{-6}$ $R_{window}=5.935\cdot 10^{-7}$ Эквивалантное для всего помещения: $R_{equivalent} =\frac{R_{wall}\cdot R_{window}}{R_{wall}+R_{window}}$ $R = 4.329\cdot 10^{-7}$	ч. $\cdot$ К/Дж
cair	Теплоемкость воздуха Сair = 1005.4	Дж/(кг $\cdot$ К)
Mheater_air	Расход воздуха постоянный Mheater_air = 3600	кг/ч.
Theater	Температура в работающем нагревателе Theater = 50	град. С

5. Создание компонентов модели

Компоненты модели это по своей сути записи математических уравнений в структурном виде. Либо текст на языке программирования, повторяющий математические уравнения. Для структурного моделирования, так же как и для выполнения программы нам необходимы данные, поэтому модель формируется только после сбора исходных данных. Если данных по объекту нет, то их приходится брать из справочников, принимать по аналогии, выдумывать в конце концов. Без данных модель не считает, и программа не выполняется.

Структурное моделирование — это разделение системы модели на части и последовательный переход от модели компонентов к обще модели. Это как интеграл, который нужно брать частями. Или слон, которого едят по частям. Сначала создаются отдельные модели элементов. Затем они отлаживается независимо от основной системы. И только убедившись, что модель компонента работает, как ожидается переходим к следующему шагу. Казалось бы очевидно, но в практике уже не раз встречался, когда создается гигантская модель, а потом долго и мучительно отлаживается.

4.1 Модель нагревателя.

Модель нагревателя реализует расчет количества тепла, переданного к нагреваемому воздуху:

$\frac{dQ_{gain}}{dt}=M_{heater-air}\cdot c_{air}(T_{heater}-T_{room})$

В качестве входных данных используется температура воздуха, поступающего в нагреватель из помещения, а также сигнал от контроллера, который равен 0 при выключенном нагревателе и 1 при включенном.

В качестве выходных данных мы получаем мощность теплового потока из нагревателя.

Необходимые для расчета параметры расхода воздуха, теплоемкости и температуры нагретого воздуха мы задаем в глобальных переменных проекта. (см. рис. 3)

Важное замечание: в Таблице 1 у нас не все размерности заданы в С. В частности, для времени мы везде использовали размерность час. Это позволяет при моделировании использовать масштаб времени «часы», одна единица по времени моделирование равна 1 часу.

Рисунок 3. Структурная схема модели нагревателя.

Тестирование модели нагревателя

Для проверки работоспособности модели компонента мы создаем тестовое окружение, которое выдаёт заданные сигналы на модели, и мы выводит результаты моделирования на график, что позволяет сделать вывод об адекватности модели компонента.

В качестве тестовых сигналов мы используем:

Для сигнала управления control ступеньку, которая выдает 1 на первых 5 часах модельного времени и 0 после.

В качестве тестового сигнала температуры подаем синусоиду с амплитудой 10, с помощью линейной функции, сдвинутой на 20 градусов вверх.

Тестовая модель и результаты тестирования представлены на рисунке 4.

Рисунок 4. Тестирование модели нагревателя.

Видно, что при включенном контроллере (синяя линия), повышение температуры (зеленая линия) в комнате вызывает снижение энергии, передаваемой нагревателям в помещение. После выключения поток энергии падает до 0. Тестирование показывает, что модель нагревателя работает так, как мы ожидали.

5.2 Модель контроллера

В качестве контроллера на первом этапе используем простую релейную схему. Алгоритм работы такой: если температура меньше уставки на 2 градуса, то включаем нагреватель, если температура больше уставки на 2 градуса, то выключаем нагреватель. Схема такого контроллера представлена на рисунке 4.

Рисунок 5. Схема контроллера

Тестирование модели контроллера

Для тестирования модели контроллера мы подаем тот же самый синусоидальный сигнал с амплитудой 10 градусов и нулевым значением, сдвинутым на 20 градусов. Схема проверки и результат моделирования представлены на рисунке 6. Анализ результатов показывает, что пока температура выше 18 градусов (красная линия на графике рис. 6), сигнал контроллера — 0 (зеленая линия на графике), как только температура снижается ниже 18 градусов (на два градуса ниже уставки), сигнал контроллера становится равным 1. Как только температура превышает 22 градуса (на два градуса выше уставки), сигнал контроллера становится равным 0.

Рисунок 6. Тестирование модели контроллера

5.3 Модель помещения

В качестве основного уравнения температуры мы используем основное уравнение см. формулу 1.

$\frac{dT_{room}}{dt}=\frac{1}{m_{room}\cdot c_{air}}\left[\frac{dQ_{gain}}{dt}-\frac{dQ_{loss}}{dt}\right]$

Для расчета потерь в окружающую среду используется формула 3

$\frac{dQ_{loss}}{dt}=\frac{T_{room}-T_{outside}}{R}$

Общая структурная модель помещения выглядит, как показано на рисунке 7. Все параметры мы рассчитываем в скрипте субмодели.

Рисунок 7. Модель помещения.

Тестирование модели помещения

Для тестирования модели помещения используем следующие сигналы:

Постоянная внешняя температура 15 град и ступенчатое изменение потока энергии: в начальный момент времени поток равен 0, в момент 5 часов, ступенькой поднимается до 5000 кДж/час. Результат тестирования представлен на рисунке 8.

Рисунок 8. Тестирование модели помещения.

При отсутствии подогрева в начальный момент времени температура в помещении, заданная начальными условия в интеграторе в 20 градусов, за счет теплообмена с внешней средой опускается до температуры окружающей среды. Затем после включения нагревателя температура повышается и устанавливается на новом уровне, где поток полученного тепла уравновешивается тепловыми потерями во внешнюю среду. В этом можно также убедиться, если задать время расчета 24 часа, и выполнив просмотр значений на линии связи в конце расчета (см. рис. 9).

Рисунок 9. Установившиеся параметры модели в конце расчета.

6. Создание комплексной модели

Комплексная модель должна создаваться из отдельных отлаженных элементов. Можно создавать отдельные элементы модели и потом их объединять, можно последовательно добавлять в модель системы новые элементы, каждый раз проверяя что усложненная модель работает корректно. В этом случае локализации ошибки значительно упрощается.

Интеграция контроллера и нагревателя

После отладки каждого компонента отдельно приступаем к созданию комплексной модели, включающей все компоненты. Данный процесс можно также выполнять последовательно. Например, соединив в модель только нагреватель и контроллер, можно убедиться, что эти два компонента работают совместно корректно.

Например, на рисунке 10 показано совместное тестирование модели контроллера с нагревателем, где в качестве тестовых условий задана температура в комнате в виде синусоиды и заданная температура уставки в 20 градусов.

Рисунок 10. Тестирование контроллера с нагревателем.

Тест показывает адекватность работы совместной модели контроллера и нагревателя. С помощью курсора на графике (см. рис. 10) можно убедиться, что:

1) включение обогревателя происходит при снижении температуры ниже 18 градусов;

2) отключение обогревателя происходит при повышении температуры выше 22 градусов;

3) отдаваемое тепло обогревателя растет, когда температура входного воздуха падает.

Мы убеждаемся, что два компонента модели совместно работают адекватно.

Полная модель

Добавляем в комплексную модель компонент помещение и замыкаем соответствующие связи.

В качестве тестового воздействия задаем синусоидальный сигнал, имитирующий внешнюю температуру с амплитудой 20 градусов и частотой 0,25. Схема модели и результат расчета представлены на рисунке 11.

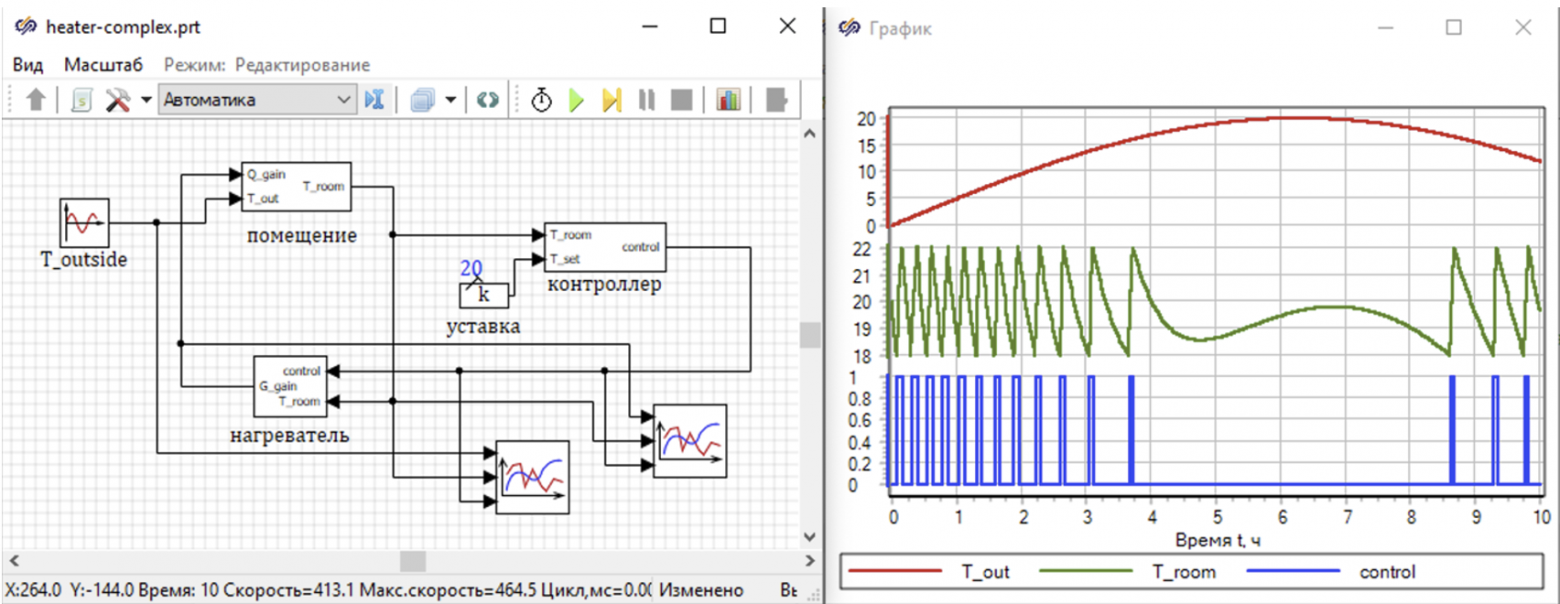Рисунок 11. Комплексная модели и результат расчета.

На графиках рис. 11 видно, что система включает и выключает нагреватель (синяя линия) при достижении температуры в помещении (зеленая линия) верхней (18 град.) и нижней (22 град.) границы переключения в контроллере.

Также видно, что чем выше температура окружающей среды (красная линия), тем реже включается нагреватель, в то время как температура окружающей среды выше 18 градусов, нагреватель вообще не включается.

Примерно с 5 часов до 7 часов происходит рост температуры в помещении за счет роста температуры наружного воздуха.

На рисунке 12 представлены графики теплового потока (красная линия), температуры в комнате (зеленая линия) и управляющего воздействия (синяя линия). Из графиков видно, что мощность теплового потока нагревателя появляется только при включении и по мере роста температуры в комнате снижается, что адекватно отражает заложенные в модель уравнения.

Также из графика 12 видно, что время включения нагревателя сокращается, поскольку чем меньше тепловой поток потерь, тем меньше нужно времени, чтобы нагреть постоянный объем воздуха от 18 до 22 градусов.

Рисунок 12. Результаты тестирования комплексной модели.

7. Валидация модели на реальных данных

Если есть реальные данные, то модель может быть и должна быть проверена для оценки ее адекватность. В случае разработки новых изделий модель может быть проверена на данных, полученных для аналогичных систем. Например, в ядерной энергетике используется аттестация математических моделей, процесс, когда математическая модель проверяется на известных экспериментальных данных.

Загрузка данных в модель

Созданная и отлаженная модель может уже использоваться с реальными данными. В качестве примера возьмём суточные температуры г. Саров 25 мая 2022 года.

На следующем рисунке данные из Google

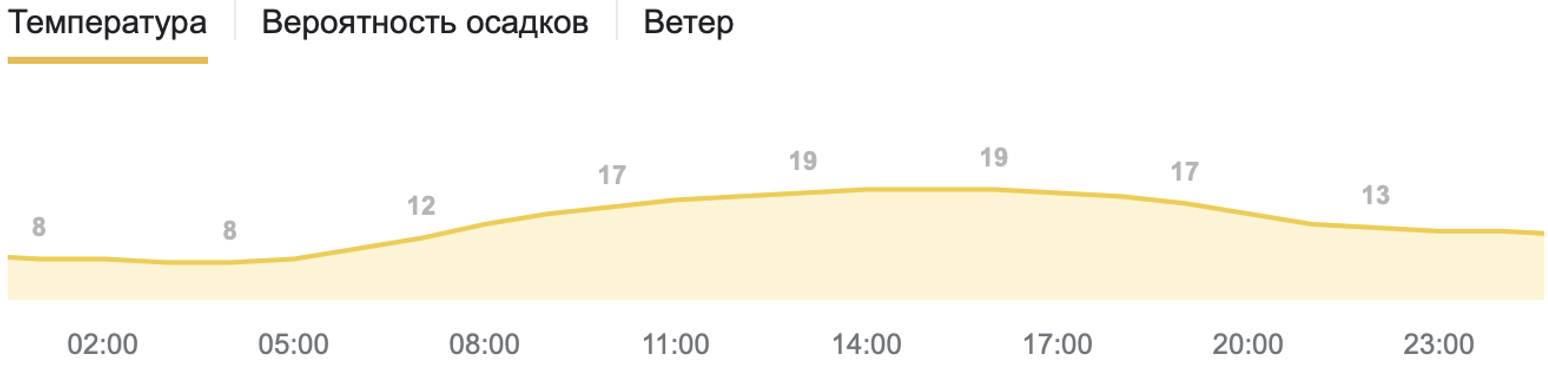Рисунок 13. Дневные температуры окружающей среды

Для использования реальных данных создадим новую субмодель, в которой осуществляется вывод температуры в зависимости от расчётного времени модели. Для этого создадим табличный файл данных, например в Excel, в котором сохраним таблицу данных.

Далее этот файл прочитаем блоком «чтение таблиц» и передадим значения в блок интерполяции. Для блока интерполяции используем модельное время в качестве аргумента, на выходе получаем температуру суток, соответствующую текущему модельном времени.

Рисунок 14. Настройка загрузки реальных данных в модель.

Подключаем выход данного блока вместо тестового синусоидального сигнала в комплексную модель. Модель и результаты расчета представлены на рисунке 15.

Рисунок 15 Комплексная модель с реальными данными и результатом расчета.

Сравнение с экспериментальными данными

После получения расчёта c использованием реальных температур окружающей среды можно определить, насколько наша модель отвечает реальности. Сравним. Например, у нас есть файл измерения температуры в помещении, записанный с шагом 6 минут (0.1 часа модельного времени), в тот же самый день, для которого мы использовали данные по наружной температуре.

В нашем учебном примере данные измерения находятся в файле sample_room_temp-2.dat. Добавим в модель блок чтение данных и выведем их на один график:

Рисунок 16. Схема сравнения модели с измеренными данными.

Результаты сравнения модельных и измеренных данных представлены на рис. 17.

Рисунок 17. Рассчитанная и измеренная температуры в помещении. Рисунок 17. Рассчитанная и измеренная температуры в помещении.

Анализ показывает, что качественно наша модель ведет себя очень похоже на реальный объект, особенно с учетом дискретности измерений. Однако в длительном процессе отклонения между моделью и реальными измерения нарастают. Очевидной причиной в нашем случае может быть неверно рассчитанное термическое сопротивление стен и окон, поскольку, например, окна могут иметь зазоры, в стенах существовать тепловые перемычки, за счет чего общее термическое сопротивление помещения снижается.

Вопрос в том, насколько это несоответствие, влияет на работу с моделью? Это определяется целями нашего моделирования. Если увеличить первую часть графика, то видно, что в течение первых 0.5 часа совпадение модели и измеренных значений практически идеальное (с учетом дискретности измерений) — см. рис. 18

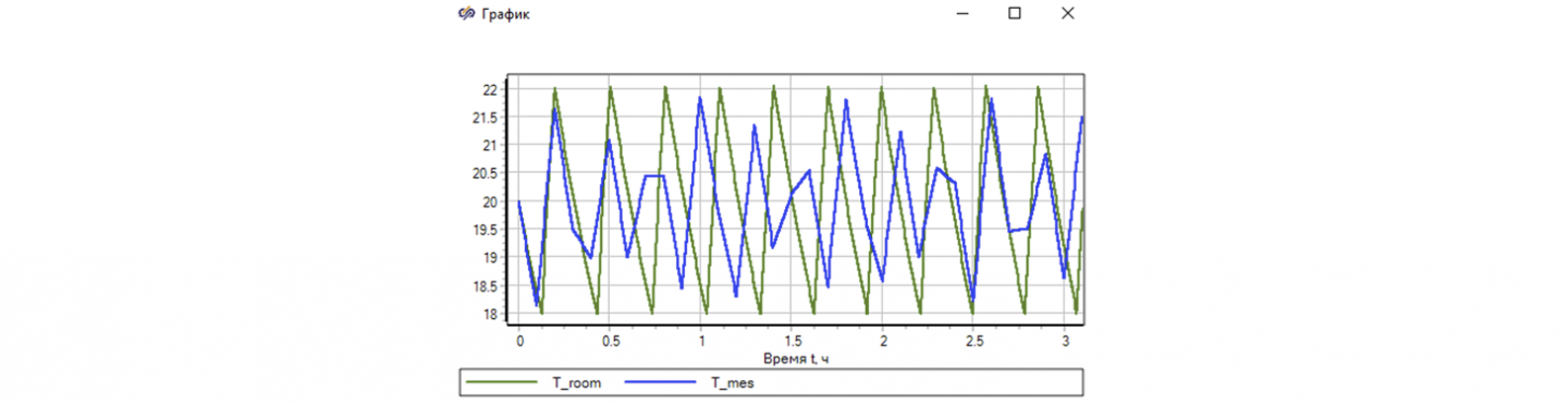Рисунок 18. Сравнение расчета и измерений в начальный период расчета.

Таким образом, если исследуем процессы длительностью менее 30 минут, например, для настройки оперативного регулятора, оценки скорости нагрева и охлаждения, такая модель вполне себе может применяться. Однако, в целях моделирования стоит расчет энергии необходимого на обогрев данного помещения. В этом случае малое отклонение накапливается, и мы получим совсем не тот результат, который нам необходим.

В случае отклонений, связанных с неидеальностью реализации объекта (зазоры, внутренние тепловые перемычки, отклонения размеров), обычно невозможно посчитать отклонения по поточным формулам. Но это можно сделать путем сравнения измерений с моделью.

8. Коррекция модели по экспериментальным данным.

Коррекция модели может происходит как путем добавления новых уравнении в математическую модель и (или) изменения структуры, так и простым исправлением коэффициентов в уравнениях. В последнем случае коррекция модели сильно упрощается и можно использовать автоматические средства оптимизации.

Для коррекции модели воспользуемся блоком оптимизации.

В качестве оптимизируемого параметра используем термическое сопротивление помещения, а в качестве критерия оптимизации — разницы между измеренным значением температуры в помещении и рассчитываемым в модели. Расчетная схема оптимизации представлена на рисунке 19.

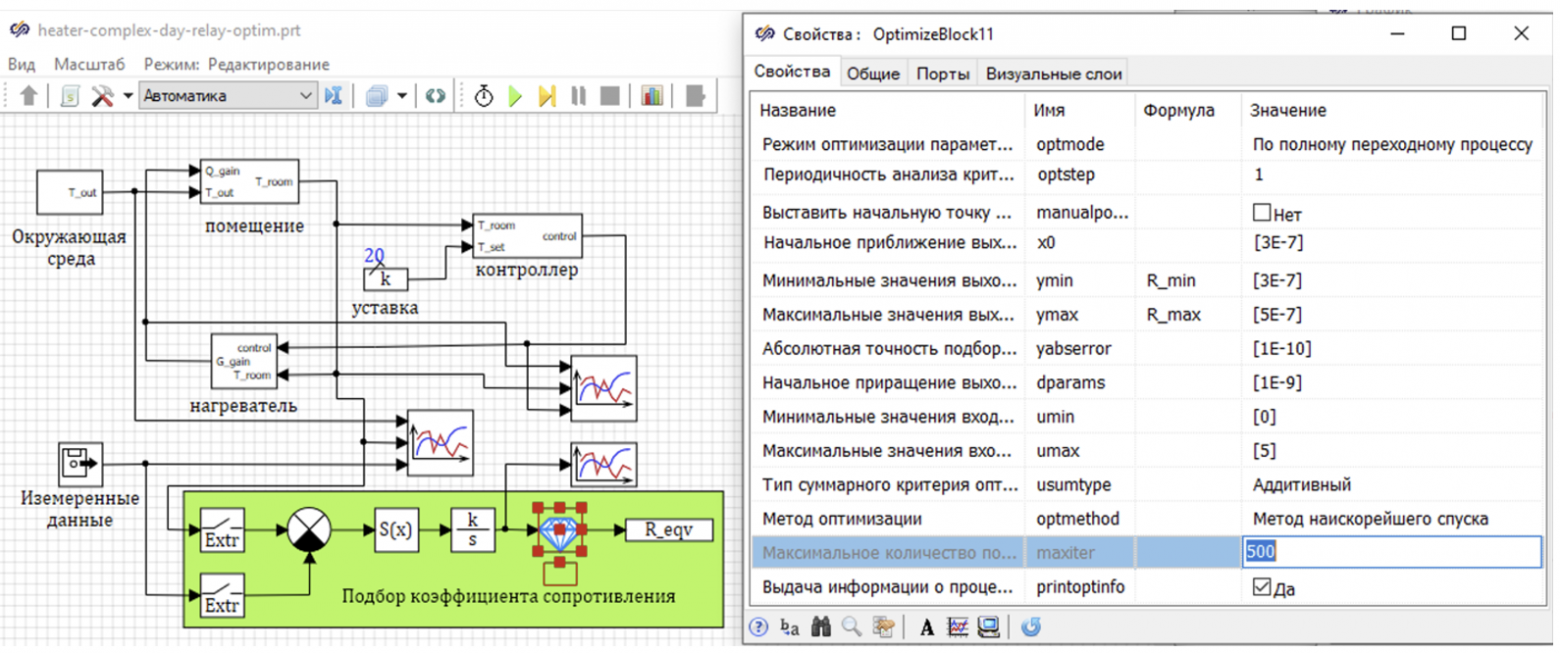Рисунок 19. Схема подбора термического сопротивления.

Поскольку измерение параметров происходит с частотой 0.1 часа, то при сравнении модели и измерений мы получаем отклонение, связанное не только с недостатками модели, но и с дискретностью измерения (см. рис. 18). Чтобы исключить из сравнения ошибки дискретности, мы дискредитируем расчетную величину с частотой измерений. После этого мы сравниваем два дискретных значения, определяем среднеквадратичное отклонение и интегрируем (накапливая ошибку). Таким образом, интеграл среднеквадратичной ошибки является критерием, который мы отправляем в блок оптимизации. Блок оптимизации подбирает такое значение термического сопротивления, чтобы ошибка была минимальной.

В результате подбора коэффициента, мы получаем скорректированное значение термического сопротивления для помещения: R_eqv = 3.684. См. рис. 20.

Рисунок 20. Результат настройки модели по измерениям.

Сравнение графиков до настройки модели и после (рис. 20 и рис. 17) показывает, что после корректировки термического сопротивления наша модель корректно отражает изменение температуры в течение 24 часов и может использоваться для оценки энергии, требуемой для поддержания температуры при различных условиях окружающей среды в течение суток.

На рисунке 21 предоставлено сравнение температуры до настройки и после в первые 3 часа моделирования.

Видно, что настройка модели обеспечивает нивелирование частоты измерений, таким образом настроенная модель позволяет также восстановить недостающие данные измерений.

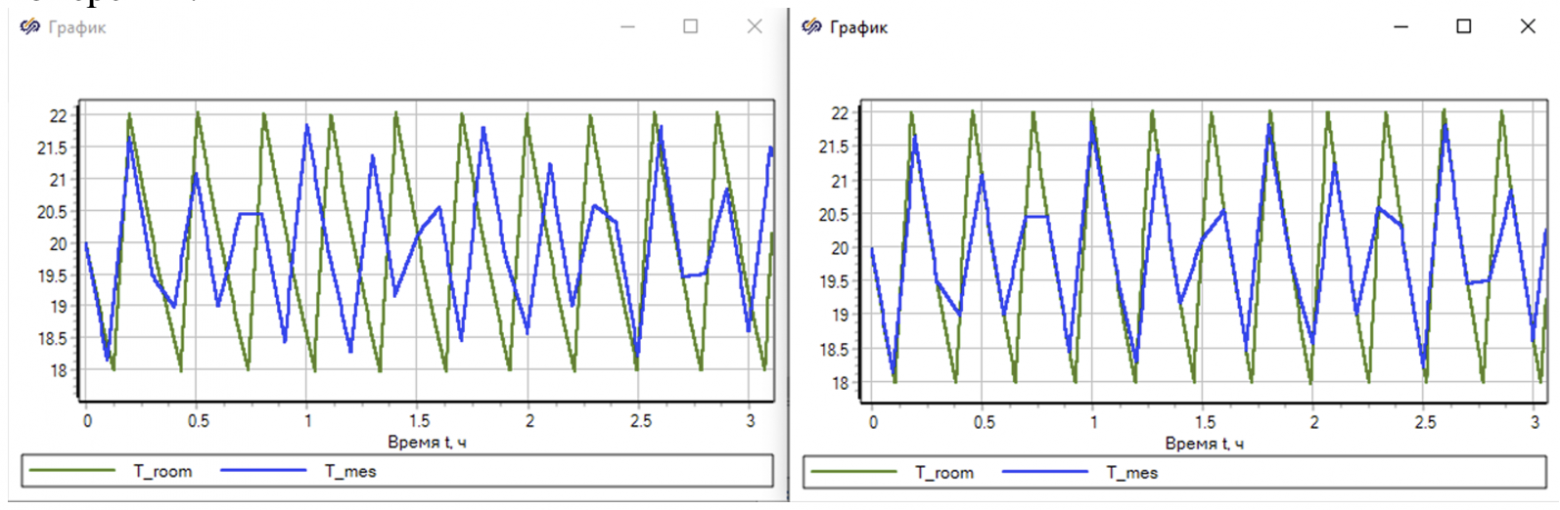Рисунок 21. Графики температуры модели и измерения до настройки и после.

Модели из статьи можно взять по ссылки здесь…

В заключение советы начинающим

Модель должна отвечать целям моделирования. Делай просто то, что можно сделать просто, а что нельзя то не делай :)

Всегда соблюдай последоватльность действий. Не стой на телеге впереди паравоза :)

Используй реальные данные и поправочные коэффициенты, подгон решения под ответ не всегда плохо, а иногда и хорошо :)