[Перевод] Существует ли частотная область в реальности?09.04.2024 18:00

Частотная область — волшебное математическое пространство, которое трансформирует комплексные сигналы в амплитуды и фазы синусоид. Она открывает нам возможность применять разнообразные методы обработки сигналов, казавшиеся почти недостижимыми при их анализе в наиболее очевидной форме, а именно — во временной области.

Изображение волнового рисунка (выше) и визуализация частотного спектра (ниже) композиции

Изображение волнового рисунка (выше) и визуализация частотного спектра (ниже) композиции «Girl in Blue»

Однако насколько материально частотное пространство? Дискретное преобразование Фурье (DFT) имеет ключевое значение в сферах связи и анализа сигналов, но не раскрывает ли оно более глубокие, скрытые аспекты реальности? Рассмотрим, к примеру, квадратные волны. Действительно ли они существуют, если преобразование Фурье разлагает их на ряд нечетных гармоник синусоид, которые, в свою очередь, эффективно предсказывают поведение электронных схем в реальном мире?

Сегодня я хочу немного уменьшить роль преобразования Фурье, сняв его с постамента. Несомненно, синусоидальные волны являются повсеместными в природе и служат мощным аналитическим инструментом для множества задач. Однако возможно создание иных частотных областей с хорошими свойствами, которые подчиняются другим принципам. К таким областям можно отнести ту, где реальностью являются исключительно квадратные волны, а все остальное представляет собой лишь гармонические составляющие.

Дискретное косинусное преобразование (DCT)

Для начала давайте обратимся к дискретному косинусному преобразованию — это упрощенный вариант дискретного преобразования Фурье, который задействует только реальные числа. Вспомним формулу DCT-II:

$F_k = \sum^{\substack{ N - 1 }}_{\substack{ n = 0 }} s_n \cdot cos(\pi k \frac{n+\frac12 }{N} )$

Этот процесс заключается в поочередном взятии ряда входных данных (например, аудиосемплов sn), умножении их на определенные значения косинусной функции и последующем суммировании полученных результатов для определения амплитуды на конкретной частоте ( F_k ).

Основа данного алгоритма представляет собой функцию cos() , создающую синусоиду с частотой, соответствующей индексу текущего частотного бина DCT. Эта функция называется базисной функцией. Мы можем отвлечься от конкретной формы и переформулировать выражение следующим образом:

$F_k = \sum \limits_{n=0}^{N-1} s_n \cdot B(k,n)$

В этой универсальной формулировке для перехода к частотному представлению, B(k,n) определяет некий коэффициент, зависящий от значений и . Программисты могут воспринимать B(k,n) как таблицу для быстрого поиска значений. Предлагаю вычислить эту таблицу — или матрицу в математическом смысле — для N равного 16:

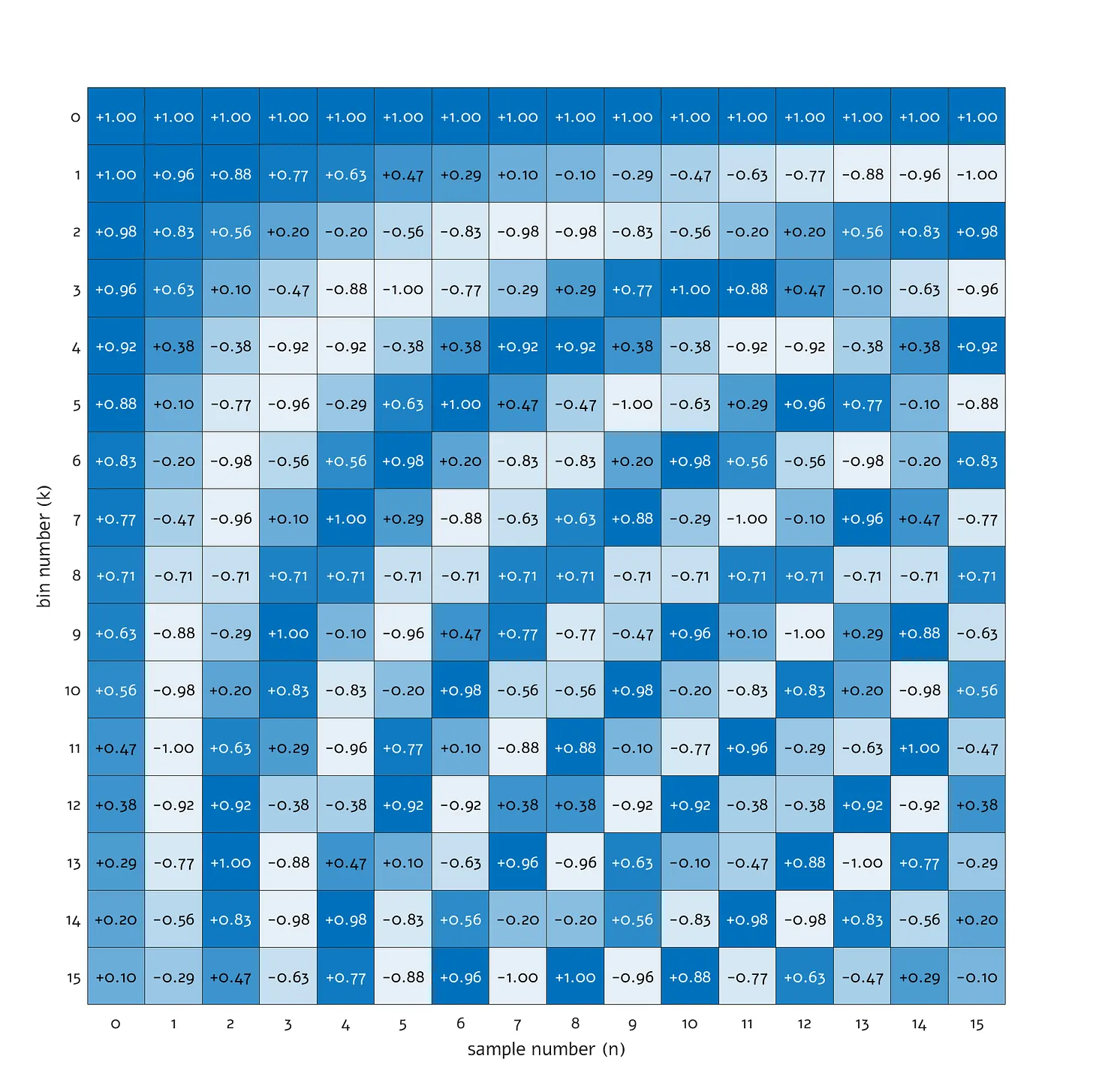
График базовой функции DCT-II для N=16

Если вы знакомы с операцией DCT, то этот визуальный материал окажется для вас понятным. Первая строка ( k=0 ) соответствует постоянной составляющей (DC) — это косинус с нулевой частотой, который постоянно равен +1.00. Следующая строка представляет косинус, проходящий через половину своего периода от +1.00 до -1.00; далее идет строка для полного цикла косинуса при k=2 , затем цикл и половина при k=3 и так далее.

Вселенная квадратных волн

Каким образом можно создать новую базисную функцию, которая вместо разложения сигналов на синусоидальные частоты будет разделять их на квадратные волны? Заглядывая немного вперед, ответ удивительно прост:

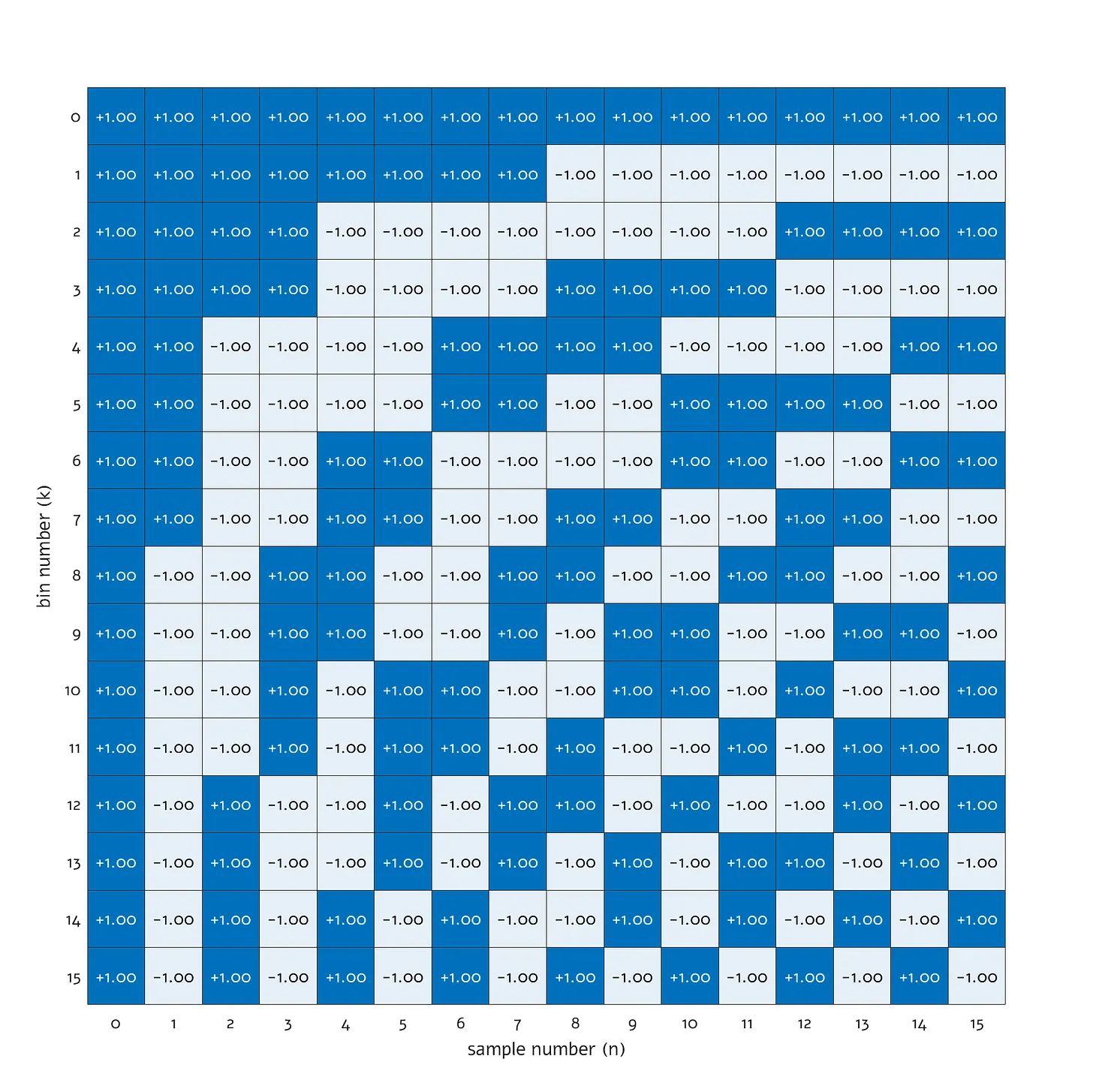
Матрица Уолша для N=16

Эта конструкция известна как матрица Уолша. Она составлена из квадратных волн, которые изменяют свою частоту, и содержит в себе определенные сложные симметрии. Каждый элемент матрицы представляет собой либо +1, либо -1, что делает вычисления относительно простыми — достаточно изменить знаки входных данных и выполнить их суммирование.

На первый взгляд, матрица может показаться простой, но разработка ее структуры требует времени. Чтобы охватить всю информацию о частоте и фазе, строки располагаются в порядке увеличения количества изменений знака — каждая последующая строка содержит на один переменный знак больше, чем предыдущая. Кроме того, узор матрицы тщательно сконструирован так, чтобы обеспечивать ортогональность — это особый вид симметрии между входом и выходом, который позволяет безошибочно выполнять преобразования между частотным представлением и временными данными.

Учитывая сложность структуры матрицы Уолша, одним из наиболее эффективных методов ее создания является начало с формирования так называемой матрицы Хадамара. Для размерности N=16 эта промежуточная структура выглядит следующим образом:

Матрица Хадамара для N=16

Введение в мир Хадамара

На первый взгляд, диаграмма может показаться беспорядочной, но на деле это всего лишь вариация распределения Уолша. К примеру, строки #1 и #8 меняются местами; аналогичная ситуация происходит между строками #1 и #15. В отличие от Уолша, эта структура, которая напоминает фрактал, на удивление проста для создания с нуля.

Чтобы приступить к формированию матрицы Хадамара, мы начнем с самого основного одномерного массива размером 1×1:

$H_0 = \begin{bmatrix} +1 \end{bmatrix}$

Исходя из этого, мы последовательно увеличиваем размер массива, используя массив, созданный на предыдущем этапе ( $H_{n-1}$ ). Мы размещаем четыре его копии на решетке, которая вдвое превышает исходные размеры. Первые три копии оставляем без изменений, а четвертую — расположенную в нижнем правом углу — инвертируем по знаку. Математическое выражение для этого процесса расширения выглядит следующим образом:

$H_n = N_{n-1} \otimes \begin{bmatrix} +1 & +1 \\ +1 & -1\end{bmatrix}$

Этот изящный оператор ⊗ называется кронекеровым произведением, хотя в действительности он представляет собой лишь изысканный способ копирования и вставки. Первое увеличение массива выглядит так:

$H_1 = \begin{bmatrix} \begin{array}{c|c} +1 & +1 \\ \hline +1 & -1\end{array}\end{bmatrix}$

Еще одна итерация дает нам:

$H_2 = \begin{bmatrix} \begin{array}{c c| c c} +1 & +1 & +1 & +1 \\ +1 & -1 & +1 & -1 \\ \hline+1 &+1 &-1 &-1 \\ +1 &-1 &-1 &+1 \end{array} \end{bmatrix}$

Этот процесс идет дальше. Размер конечной матрицы Хадамара всегда составляет $2^n \times 2^n$ , где обозначает число выполненных этапов построения.

Хотя на компьютере можно вычислить матрицу, следуя указанному алгоритму компоновки, существует элегантный метод с использованием битовых операций, который может служить альтернативой: оказывается, чтобы определить значение функции Хадамара для любой конкретной ячейки, достаточно вычислить побитовое И (x & y) координат этой ячейки и определить, четным или нечетным является количество установленных битов в полученном результате. Ниже представлен код на языке C, который выполняет эту задачу и выводит на экран матрицу Хадамара размером 8×8:

#include 
#include 

#define HD_LEN_POW2 3
#define HD_LEN      (1 << HD_LEN_POW2)

int8_t hadamard(uint32_t x, uint32_t y) {  
  return (__builtin_popcount(x & y) % 2) ? -1 : 1;
}

int main() {
  for (uint32_t y = 0; y < HD_LEN; y++) {
    for (uint32_t x = 0; x < HD_LEN; x++) printf("%+d ", hadamard(x, y));
    putchar('\n');
  }
}

В основном, данная матрица обеспечивает все необходимое для создания преобразования в частотную область. Тем не менее, расположение частотных интервалов в ней является неупорядоченным. Давайте попытаемся упорядочить их, прежде чем завершить.

Войдите, господин Уолш

Для того чтобы преобразовать матрицу Хадамара в упорядоченную форму, как было показано ранее, нам необходимо отсортировать строки согласно их частотному порядку.

Самый простой метод, который можно встретить в большинстве стандартных реализаций, заключается в подсчете количества смен знаков в каждой строке. Однако пользователь на платформе Mastodon предложил еще один остроумный подход, использующий битовую арифметику: для матрицы с 2^n строками соответствие строк Хадамара может быть найдено путем выполнения операции XOR между номерами строк Уолша и их же значением, сдвинутым на один бит вправо, а затем реверсированием последних n бит.

Ниже представлена реализация, которая выполняет именно это и выводит на экран отсортированную матрицу размером 8×8:

#include 
#include 

#define HD_LEN_POW2 3
#define HD_LEN      (1 << HD_LEN_POW2)

int8_t hadamard(uint32_t x, uint32_t y) {
  return (__builtin_popcount(x & y) % 2) ? -1 : 1;
}

uint32_t to_graycode(uint32_t val) {
  return val ^ (val >> 1);
}

uint32_t reverse_bits(uint32_t val, uint8_t bit_cnt) {
  uint32_t res = 0;
  while (bit_cnt--) { res <<= 1; res |= (val & 1); val >>= 1; }
  return res;
}

int8_t walsh_array[HD_LEN][HD_LEN];

void precompute_walsh() {
  for (uint32_t y = 0; y < HD_LEN; y++) {
    uint32_t hd_y = reverse_bits(to_graycode(y), HD_LEN_POW2);
    for (int x = 0; x < HD_LEN; x++) walsh_array[y][x] = hadamard(x, hd_y);
  }
}

int main() {
  precompute_walsh();
  for (uint32_t y = 0; y < HD_LEN; y++) {
    for (uint32_t x = 0; x < HD_LEN; x++) printf("%+d ", walsh_array[y][x]);
    putchar('\n');
  }
}

С этими знаниями в распоряжении, мы в состоянии переосмыслить реализацию дискретного косинусного преобразования (DCT) и разработать «дискретное преобразование Хадамара» вместе с его инверсией:

...previous code here, sans main()...

void sqft(double* out_buf, double* in_buf, uint32_t len) {

  for (uint32_t bin_no = 0; bin_no < len; bin_no++) {
    double sum = 0;
    for (uint32_t s_no = 0; s_no < len; s_no++)
      sum += in_buf[s_no] * walsh_array[s_no][bin_no];
    out_buf[bin_no] = sum;
  }

}

void isqft(double* out_buf, double* in_buf, uint32_t len) {

  for (int s_no = 0; s_no < len; s_no++) {
    double sum = 0;
    for (int bin_no = 0; bin_no < len; bin_no++)
      sum += in_buf[bin_no] * walsh_array[bin_no][s_no];
    out_buf[s_no] = sum / len;
  }

}

Формально это преобразование именуется как Уолша-Хадамара (WHT), однако название не столь важно. Главное — удостовериться в его функционировании:

...continuing from the previous snippet...

void print_buf(const char* prefix, double* buf, uint32_t len) {
  printf("%s", prefix);
  for (uint32_t i = 0; i < len; i++) printf(" %+.2f", buf[i]);
  putchar('\n');
}

int main() {

  double in[HD_LEN] = { 1, 1, 1, 1, 5, 5, 5, 5 };
  double sq_freq[HD_LEN], out[HD_LEN];

  precompute_walsh();
  sqft(sq_freq, in, HD_LEN);
  isqft(out, sq_freq, HD_LEN);

  print_buf("Input :", in, HD_LEN);
  print_buf("SQFT  :", sq_freq, HD_LEN);
  print_buf("ISQFT :", out, HD_LEN);

  return 0;
}

В качестве входных данных мы используем последовательность чисел, имитирующую квадратную волну: 1 1 1 1 5 5 5 5. Результат применения дискретного преобразования Фурье (ДПФ) или дискретного косинусного преобразования (ДКП) будет представлять собой набор гармоник, распределенных по различным частотным интервалам:

DCT : +24.00 -10.25 -0.00 +3.60 +0.00 -2.41 -0.00 +2.04

В противоположность этому, частотный профиль, сгенерированный программой, демонстрирует ненулевые значения исключительно для F_0 (постоянная составляющая) и F_1 , что подтверждает наличие алгоритма, способного декомпозировать сигнал на чистые квадратные волны:

SQFT : +24.00 -16.00 +0.00 +0.00 +0.00 +0.00 +0.00 +0.00

В заключение, мы можем удостовериться в том, что функция обратного преобразования — isqft () — корректно конвертирует частотный спектр обратно в исходную последовательность данных:

ISQFT : +1.00 +1.00 +1.00 +1.00 +5.00 +5.00 +5.00 +5.00

Мне не удалось обнаружить визуальные сопоставления результатов работы алгоритмов, поэтому я решил создать их самостоятельно. Привожу к вашему вниманию квази-стандартную спектрограмму дискретного косинусного преобразования (ДКП) для 11-секундного фрагмента песни «DARE» группы Gorillaz:

Классическая спектрограмма синусоидального сигнала

И в качестве сравнения, вот изящная эквивалентная спектрограмма, выполненная с использованием преобразования Уолша-Хадамара:

Дебют спектрограммы квадратной волны

Преобразование Уолша-Хадамара, благодаря своей вычислительной эффективности и хорошей пригодности для определенных типов данных, находит применение в нескольких узких областях. Не в том дело, что его нужно использовать больше; просто дискретное преобразование Фурье не является единственным истинным методом.