[Перевод] Регулярные выражения: никакой магии
Код этого поста, как и сам пост, выложен на github.
До недавнего времени регулярные выражения казались мне какой-то магией. Я никак не мог понять, как можно определить, соответствует ли строка заданному регулярному выражению. А теперь я это понял! Ниже представлена реализация простого движка регулярных выражений менее чем в 200 строках кода.
Часть 1: Парсинг
Спецификация
Реализация регулярных выражений полностью — довольно сложная задача; хуже того, она мало чему вас научит. Реализуемой нами версии достаточно для того, чтобы изучить тему, не скатываясь в рутину. Наш язык регулярных выражений будет поддерживать следующее:
.: соответствие любому символу|: соответствиеabcилиcde+: соответствие одному или более предыдущего паттерна*: соответствие 0 или более предыдущего паттерна(и)для группировки
Хотя набор опций невелик, с его помощью можно создать интересные regex-ы, например, m (t|n| ) | b позволяющий найти субтитры к Star Wars без субтитров к Star Trek, или (..)* для нахождения множества всех строк чётной длины.
План атаки
Мы будем анализировать регулярные выражения в три этапа:
- Парсинг (синтаксический анализ) регулярного выражения в синтаксическое дерево
- Преобразование синтаксического дерева в конечный автомат
- Анализ конечного автомата для нашей строки
Для анализа регулярных выражений (подробнее об этом ниже) мы будем использовать конечный автомат под названием NFA. На высоком уровне NFA будет представлять наш regex. При получении входных данных мы будем перемещаться в NFA от состояния к состоянию. Если мы придём в точку, из которой невозможно совершить допустимого перехода, то регулярное выражение не соответствует строке.
Такой подход первым продемонстрировал один из авторов Unix Кен Томпсон. В его статье 1968 года в журнале CACM он изложил принципы реализации текстового редактора и добавил этот подход как интерпретатор регулярных выражений. Единственная разница в том, что его статья была написана в машинном коде 7094. В то время всё было намного хардкорнее.
Этот алгоритм является упрощением того, как движки без обратного просмотра наподобие RE2 анализируют регулярные выражения за доказуемо линейное время. Он сильно отличается от движков regex из Python и Java, в которых применяется обратный просмотр. Для заданных входных данных при малых строках они выполняются практически бесконечно. Наша реализация будет выполняться за O(length(input) * length(expression).
Мой подход приблизительно соответствует стратегии, изложенной Рассом Коксом в его потрясающем посте.
Представление регулярного выражения
Давайте отступим назад и подумаем о том, как представить регулярное выражение. Прежде чем приступать к анализу регулярного выражения, нам нужно преобразовать его в структуру данных, с которой сможет работать компьютер. Хотя строки обладают линейной структурой, регулярные выражения имеют естественную иерархию.
Давайте рассмотрим строку abc|(c|(de)). Если бы мы оставили её строкой, то нам пришлось бы возвращаться назад и выполнять переходы, отслеживая различные наборы скобок при анализе выражения. Одним из решений является преобразование его в дерево, которое компьютер с лёгкостью сможет обходить. Например, b+a превратится в следующее:
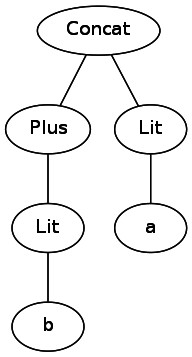
Чтобы представить дерево, нам нужно создать иерархию классов. Например, наш класс Or должен иметь два поддерева, представляющих обе его стороны. Из спецификации понятно, что нам нужно распознавать четыре разных компонента регулярных выражений: +, *, | и символьные литералы наподобие ., a и b. Кроме того, нам также нужно представлять случаи, когда одно выражение следует за другим. Вот какими будут наши классы:
abstract class RegexExpr
// ., a, b
case class Literal(c: Char) extends RegexExpr
// a|b
case class Or(expr1: RegexExpr, expr2: RegexExpr) extends RegexExpr
// ab -> Concat(a,b); abc -> Concat(a, Concat(b, c))
case class Concat(first: RegexExpr, second: RegexExpr) extends RegexExpr
// a*
case class Repeat(expr: RegexExpr) extends RegexExpr
// a+
case class Plus(expr: RegexExpr) extends RegexExprПарсинг регулярного выражения
Чтобы перейти от строки к представлению в виде дерева, нам нужно воспользоваться процессом преобразования, известным как «парсинг (синтаксический анализ)». Я не буду подробно рассказывать о построении парсеров. Вместо этого я изложу информацию, которой достаточно, чтобы указать вам в нужном направлении, если вы решите написать собственный. Я вкратце расскажу о том, как выполнял парсинг регулярный выражений с помощью parser combinator library Scala.
Библиотека парсера Scala позволяет нам написать парсер, просто написав набор описывающих наш язык правил. К сожалению, в нём используется множество бестолковых символов, но я надеюсь, вам удастся пробраться сквозь шум и получить общее понимание о происходящем.
При реализации парсера нам необходимо определить порядок операций. Так же как в арифметике применяется PEMDAS [прим. пер. Parentheses, Exponents, Multiplication/Division, Addition/Subtraction — мнемоника, позволяющая запомнить порядок выполнения арифметических действий], так и в регулярных выражениях применяется свой набор правил. Мы можем выразить это более формально с помощью идеи «привязки» оператора к стоящему рядом символу. Различные операторы «привязываются» с разной силой — по аналогии, в выражениях типа 5+6×4 оператор * привязывается сильнее, чем +. В регулярных выражениях * привязывается сильнее, чем |. Можно было бы представить это в виде дерева, в котором слабейшие операторы находятся на вершине.
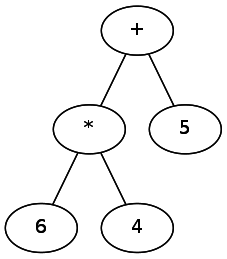
Следовательно, мы должны первыми парсить слабейшие операторы, а за ними уже более сильные операторы. При парсинге это можно представить как извлечение оператора, добавление его к дереву, а затем рекурсивную обработку оставшихся двух частей строки.
В регулярных выражениях сила привязки имеет следующий порядок:
- Символьные литералы и круглые скобки
+и*- «Конкатенация» — a следует за b
|
Так как у нас есть четыре уровня сил привязки, нам нужны четыре разных типа выражений. Мы назвали их (достаточно произвольно): lit, lowExpr (+, *), midExpr (конкатенация) и highExpr (|). Давайте перейдём к коду. Для начала мы создадим парсер для самого основного уровня, для отдельного символа:
object RegexParser extends RegexParsers {
def charLit: Parser[RegexExpr] = ("""\w""".r | ".") ^^ {
char => Literal(char.head)
}
Давайте уделим минуту объяснению синтаксиса. Код определяет парсер, собирающий RegexExpr. Правая часть говорит: «Найди что-нибудь, соответствующее \w (любому словесному символу) или точке. Если нашёл, преврати это в Literal».
Скобки должны определяться на самом низком уровне парсера, потому что они обладают самой сильной привязкой. Однако нам нужно иметь возможность поставить что-то в скобки. Мы можем добиться этого с помощью следующего кода:
def parenExpr: Parser[RegexExpr] = "(" ~> highExpr <~ ")"
def lit: Parser[RegexExpr] = charLit | parenExpr
Здесь мы определим * и +:
def repeat: Parser[RegexExpr] = lit <~ "*"
^^ { case l => Repeat(l) }
def plus: Parser[RegexExpr] = lit <~ "+"
^^ { case p => Plus(p) }
def lowExpr: Parser[RegexExpr] = repeat | plus | lit
Далее мы определим следующий уровень — конкатенацию:
def concat: Parser[RegexExpr] = rep(lowExpr)
^^ { case list => listToConcat(list)}
def midExpr: Parser[RegexExpr] = concat | lowExpr
Наконец, мы определим «или»:
def or: Parser[RegexExpr] = midExpr ~ "|" ~ midExpr
^^ { case l ~ "|" ~ r => Or(l, r)}
И в конце мы определим highExpr. highExpr — это or, слабейший оператор привязки, или если нет or, то midExpr.
def highExpr: Parser[RegexExpr] = or | midExpr
Далее добавим немного вспомогательного кода, чтобы закончить:
def listToConcat(list: List[RegexExpr]): RegexExpr = list match {
case head :: Nil => head
case head :: rest => Concat(head, listToConcat(rest))
}
def apply(input: String): Option[RegexExpr] = {
parseAll(highExpr, input) match {
case Success(result, _) => Some(result)
case failure : NoSuccess => None
}
}
}
И на этом всё! Если вы возьмёте этот код на Scala, то сможете генерировать синтаксические деревья для любого регулярного выражения, удовлетворяющего спецификации. Полученные структуры данных будут деревьями.
Теперь, когда мы можем преобразовывать наши регулярные выражения в синтаксические деревья, мы приближаемся к тому, чтобы анализировать их.
Часть 2: Генерирование NFA
Преобразование синтаксического дерева в NFA
В предыдущей части мы преобразовали представление регулярного выражения в виде плоской строки в форму иерархического синтаксического дерева. В этой части мы преобразуем синтаксическое дерево в конечный автомат. Конечный автомат приводит компоненты regex в линейный вид графа, создавая отношения «a следует за b следует за c». Представление в виде графа упростит анализ относительно потенциальной строки.
Зачем выполнять ещё одно преобразование только для того, чтобы сопоставить с regex?
Конечно, можно было бы выполнять преобразование непосредственно из строки в конечный автомат. Можно даже попробовать анализировать регулярное выражение непосредственно из синтаксического дерева или из строки. Однако при этом придётся иметь дело с гораздо более сложным кодом. Медленно понижая уровень абстракции, мы сможем обеспечить простоту понимания кода на каждом этапе. Это особенно важно при построении чего-то подобного интерпретатору регулярных выражений с практически бесконечными пограничными случаями.
NFA, DFA и вы
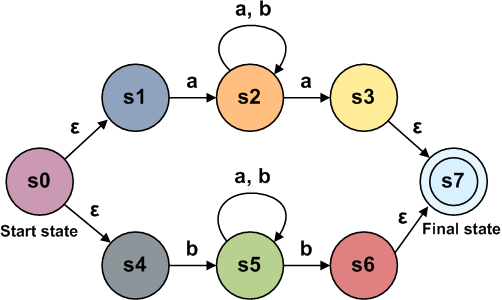
Мы будем создавать конечный автомат, называемый NFA, или nondeterministic finite automata. У него есть два типа компонентов: состояния и переходы. При представлении на схеме состояния обозначаются кругами, а переходы — стрелками. Состояние совпадения обозначается двойным кругом. Если переход помечен, то это означает, что мы должны получить этот символ на входе, чтобы совершить этот переход. Переходы также могут не иметь меток. Это значит, что мы можем совершить переход, не потребляя входные данные. Примечание: в литературе это иногда обозначается как ε. Конечный автомат, представляющий простой regex «ab»:
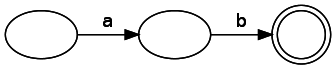
Наши узлы могут иметь для заданных входных данных несколько верных последующих состояний, так как на схеме ниже представлены два пути, при переходе из узла потребляющие одинаковые входные данные:
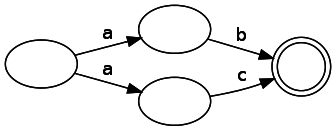
Сравните это с детерминированным конечным автоматом (DFA), в котором, как следует из его названия, заданные входные данные могут привести к единственному изменению состояния. Это снижение ограничений с одной стороны делает анализ немного сложнее, но с другой, как мы скоро увидим, значительно упрощает генерирование их из дерева. С фундаментальной точки зрения NFA и DFA аналогичны друг другу в конечных автоматах, которые они могут представлять.
Преобразование в теории
Давайте изложим стратегию преобразования синтаксического дерева в NFA. Хотя это может показаться пугающим, вы увидите, что разбив процесс на компонуемые фрагменты, мы сделаем его простым в понимании. Вспомним синтаксические элементы, которые нам нужно преобразовывать:
- Символьные литералы:
Lit(c: Char) *:Repeat(r: RegexExpr)+:Plus(r: RegexExpr)- Конкатенация:
Concat(первая: RegexExpr, вторая: RegexExpr) |:Or(a: RegexExpr, b: RegexExpr)
Последующие преобразования первоначально были изложены Томпсоном в его статье 1968 года. В схемах преобразования In будет относиться к точке входа конечного автомата, а Out — к выходной. На практике они могут быть состоянием «Match», состоянием «Start» или другими компонентами regex. Абстракция In / Out позволяет нам компоновать и сочетать конечные автоматы — важнейший вывод. Мы применим этот принцип в более общем смысле для преобразования из каждого элемента синтаксического дерева в компонуемый конечный автомат.
Давайте начнём с символьных литералов. Символьный литерал — это переход из одного состояния в другое, потребляющее входные данные. Потребление литерала «a» будет выглядеть следующим образом:
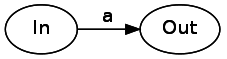
Далее давайте исследуем конкатенацию. Чтобы конкатенировать два компонента синтаксического дерева, нам нужно просто соединить их стрелкой без меток. Стоит заметить, что в этом примере, как Concat может содержать конкатенацию двух произвольных регулярных выражений, так и A с B в схеме могут быть конечными автоматами, а не только отдельными состояниями. Что-то немного странное происходит, если и A, и B оба являются литералами. Как нам соединить две стрелки без промежуточных состояний? Ответ заключается в том, что литералы могут иметь с обеих сторон фантомные состояния, чтобы сохранить целостность конечного автомата. Concat(A, B) преобразуется в следующее:

Чтобы представить Or(A, B), нам необходимо выполнить ветвление из начального состояния в два отдельных состояния. После завершения этих автоматов они оба должны указывать на последующее состояние (Out):
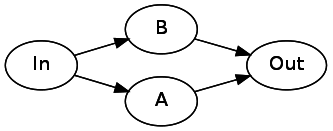
Давайте рассмотрим *. Звёздочка может быть 0 или более повторений паттерна. Чтобы реализовать это, нам нужно, чтобы одно соединение указывало непосредственно на следующее состояние, а одно возвращалось назад к текущему состоянию через A. A* будет выглядеть так:
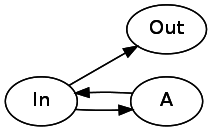
Для + мы воспользуемся небольшой хитростью. a+ — это просто aa*. Обобщая, можно переписать Plus(A) как Concat(A, Repeat(A)). Мы так и сделаем, вместо того, чтобы разрабатывать для этого случая специальный паттерн. У меня была особая причина для включения в язык +: я хотел показать, как другие, более сложные элементы регулярных выражений, которые я пропустил, часто могут выражаться в категориях нашего языка.
Преобразование на практике
Теперь, когда у нас есть теоретический план, давайте разберёмся, как реализовать его в коде. Мы будем создавать изменяемый граф для хранения нашего дерева. Хотя я предпочитаю неизменяемость, создание неизменяемых графов раздражает своей сложностью, а я ленив.
Если мы попытаемся свести представленные выше схемы в базовые компоненты, то в результате у нас получится три типа компонентов: стрелки, потребляющие входные данные, состояние совпадения и одно состояние, расщепляющееся на два состояния. Знаю, это выглядит немного странным, и потенциально незавершённым. Вам остаётся только довериться мне в том, что такое решение приведёт к самому чистому коду. Вот наши три класса компонентов NFA:
abstract class State
class Consume(val c: Char, val out: State) extends State
class Split(val out1: State, val out2: State) extends State
case class Match() extends State
Примечание: я сделал Match case-классом вместо регулярного класса. Case-классы в Scala дают классу по умолчанию удобные характеристики. Я использовал его, потому что он даёт эквивалентность на основе значений. Это делает все объекты Match эквивалентными — полезное свойство. Для других типов компонентов NFA нам нужна эквивалентность ссылок.
Наш код будет рекурсивно обходить синтаксическое дерево, сохраняя как параметр объект andThen. andThen — это то, что мы будем прикреплять свободным выходам нашего выражения. Он требуется потому, что в произвольной ветке синтаксического дерева недостаточно контекста того, что будет идти дальше — andThen позволяет нам передавать этот контекст вниз при рекурсивном обходе. Также он предоставляет нам простой способ присоединения состояния Match.
Когда дело доходит до обработки Repeat, у нас возникает проблема. andThen для Repeat сам по себе является расщепляющим оператором. Чтобы справиться с этой проблемой, мы введём заполнитель (placeholder), который позволит привязать его позже. Мы представим заполнитель следующим классом:
class Placeholder(var pointingTo: State) extends Statevar в Placeholder означает, что pointingTo изменяемо. Это изолированная часть изменяемости, позволяющая нам удобно создавать циклический граф. Все другие члены неизменны.
Начнём с того, что andThen является Match(). Это означает, что мы создадим конечный автомат, соответствующий нашему Regex, который затем может перейти в состояние Match без потребления входящих данных. Код будет коротким, но насыщенным:
object NFA {
def regexToNFA(regex: RegexExpr): State =
regexToNFA(regex, Match())
private def regexToNFA(regex: RegexExpr,
andThen: State): State = {
regex match {
case Literal(c) => new Consume(c, andThen)
case Concat(first, second) => {
// Сначала first в NFA. Её "выход"
// будет результатом преобразования second в NFA.
regexToNFA(first, regexToNFA(second, andThen))
}
case Or(l, r) => new Split(
regexToNFA(l, andThen),
regexToNFA(r, andThen)
)
case Repeat(r) =>
val placeholder = new Placeholder(null)
val split = new Split(
// Один путь ведёт к заполнителю,
// а другой - обратно к r
regexToNFA(r, placeholder),
andThen
)
placeholder.pointingTo = split
placeholder
case Plus(r) =>
regexToNFA(Concat(r, Repeat(r)), andThen)
}
}
}
И на этом всё! Соотношение предложений к строкам кода в этой части довольно высоко — каждая строка кодирует множество информации, но всё сводится к преобразованиям, рассмотренным в предыдущей части. Стоит пояснить — я не просто сел и записал код в таком виде; краткость и функционал кода стали результатом нескольких итераций работы со структурами данных и алгоритмом. Чистый код писать сложно.
В процессе отладки я написал короткий скрипт для генерирования файлов dot из NFA, чтобы можно было в целях отладки видеть генерируемые NFA. Стоит заметить, что генерируемые этим кодом NFA содержат множество ненужных переходов и состояний. При написании статьи я стремился делать код как можно более простым, даже ценой производительности. Вот некоторые примеры простых регулярных выражений:
(..)*
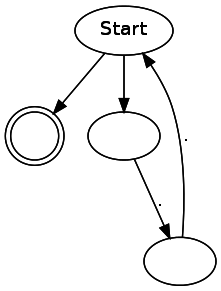
ab

a|b
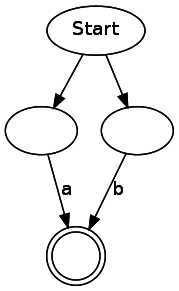
Теперь, когда у нас есть NFA (самая сложная часть), нам осталось всего лишь проанализировать его (часть полегче).
Часть 3: Анализ NFA
NFA, DFA и регулярные выражения
Во второй части мы говорили, что существует два типа конечных автоматов: детерминированные и недетерминированные. У них есть одно ключевое различие: у недетерминированного конечного автомата может быть несколько путей к одному узлу для одного токена; кроме того, по путям можно следовать без получения входных данных. С точки зрения выразительных возможностей (часто называемых «мощью»), NFA, DFA и регулярные выражения аналогичны. Это значит, что если можно выразить правило или паттерн (например, строки чётной длины) с помощью NFA, то можно также выразить его через DFA или регулярное выражение. Давайте сначала рассмотрим регулярное выражение abc*, выраженное как DFA:
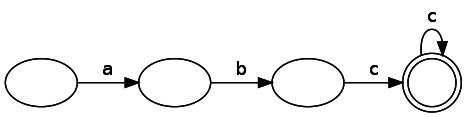
Анализ DFA прямолинеен — мы просто перемещаемся от состояния к состоянию, потребляя строку входных данных. Если мы завершаем потреблять входные данные в состоянии совпадения, то у нас есть совпадение, в противном случае его нет. С другой стороны, наш конечный автомат является NFA. Сгенерированный нашим кодом NFA для этого регулярного выражения выглядит следующим образом:
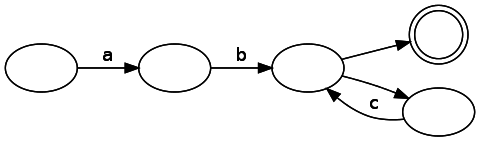
Заметьте, что здесь есть несколько непомеченных рёбер, по которым можно пройти без потребления символа. Как их эффективно отслеживать? Ответ на удивление прост: вместо отслеживания только одного возможного состояния надо хранить список состояний, в которых находится движок в текущий момент. При возникновении разветвления нужно следовать по обоим путям (превращая одно состояние в два). Если у состояния отсутствует валидный переход для текущего ввода, то оно удаляется из списка.
Здесь нужно рассмотреть два тонких момента: избежание в графе бесконечных циклов и правильная обработка переходов без входных данных. При анализе заданного состояния мы сначала переходим во все состояния для перечисления всех возможных состояний, достижимых из нашего текущего состояния, если мы не потребляем больше входных данных. На этом этапе нужно быть внимательными и хранить «множество посещённых», чтобы избежать бесконечного зацикливания в графе. Перечислив все эти состояния, мы потребляем следующий токен входных данных, или переходя в эти состояния, или удаляя их из списка.
object NFAEvaluator {
def evaluate(nfa: State, input: String): Boolean =
evaluate(Set(nfa), input)
def evaluate(nfas: Set[State], input: String): Boolean = {
input match {
case "" =>
evaluateStates(nfas, None).exists(_ == Match())
case string =>
evaluate(
evaluateStates(nfas, input.headOption),
string.tail
)
}
}
def evaluateStates(nfas: Set[State],
input: Option[Char]): Set[State] = {
val visitedStates = mutable.Set[State]()
nfas.flatMap { state =>
evaluateState(state, input, visitedStates)
}
}
def evaluateState(currentState: State, input: Option[Char],
visitedStates: mutable.Set[State]): Set[State] = {
if (visitedStates contains currentState) {
Set()
} else {
visitedStates.add(currentState)
currentState match {
case placeholder: Placeholder =>
evaluateState(
placeholder.pointingTo,
input,
visitedStates
)
case consume: Consume =>
if (Some(consume.c) == input
|| consume.c == '.') {
Set(consume.out)
} else {
Set()
}
case s: Split =>
evaluateState(s.out1, input, visitedStates) ++
evaluateState(s.out2, input, visitedStates)
case m: Match =>
if (input.isDefined) Set() else Set(Match())
}
}
}
}
И на этом всё!
Завершаем дело
Мы закончили со всем важным кодом, но API не так чист, как бы нам того хотелось. Теперь нам нужно создать интерфейс пользователя с одиночным вызовом для вызова нашего движка регулярных выражений. Мы также добавим возможность сопоставлять паттерн в любом месте строки с долей синтаксического сахара.
object Regex {
def fullMatch(input: String, pattern: String) = {
val parsed = RegexParser(pattern).getOrElse(
throw new RuntimeException("Failed to parse regex")
)
val nfa = NFA.regexToNFA(parsed)
NFAEvaluator.evaluate(nfa, input)
}
def matchAnywhere(input: String, pattern: String) =
fullMatch(input, ".*" + pattern + ".*")
}
А вот так код используется:
Regex.fullMatch("aaaaab", "a*b") // True
Regex.fullMatch("aaaabc", "a*b") // False
Regex.matchAnywhere("abcde", "cde") // True
И на этом мы закончим. Теперь у нас есть частично функциональная реализация regex всего в 106 строках. Можно добавить ещё некоторые детали, но я решил не увеличивать сложность без увеличения ценности кода:
- Классы символов
- Извлечение значений
?- Escape-символы
- И многое другое.
Надеюсь, эта простая реализация поможет вам понять, что происходит внутри движка регулярных выражений! Стоит упомянуть, что производительность интерпретатора отвратительна, поистине ужасна. Возможно, в одном из будущих постов я разберу причины этого и обсужу способы оптимизации…
