[Перевод] Раскручивая спираль: математика и галлюцинации
При попытке представить себе галлюцинации, вызванные наркотическими веществами, на ум сразу приходят закрученные, спиральные психоделические формы, напоминающие туннельное зрение. Но подобные геометрические структуры могут вызывать не только галлюционгенные наркотики вроде LSD, каннабиса или мескалина. Люди рассказывали о возникновении таких видений в момент, когда они находились при смерти, во время таких болезненных состояний, как эпилепсия и шизофрения, в результате сенсорной депривации, или даже после простого надавливания на глазные яблоки. Подобные геометрические галлюцинации так распространены, что за последнее столетие учёные начали задаваться вопросом — не могут ли они рассказать нам что-то фундаментальное о строении нашего мозга. И, судя по всему, так и есть.

Константы формы, созданные на компьютере. Два верхних изображения имитируют воронку и спираль, возникающие после приёма LSD. Нижнее левое — соты, создаваемые марихуаной. Нижнее правое — паутина.
Систематически геометрические галлюцинации впервые начал исследовать в 1920-х годах американо-немецкий психолог Генрих Клювер. Интерес Клювера к зрительному восприятию в итоге привёл его к экспериментам с пейотом, кактусом, прославленным Карлосом Кастанедой, психоактивный ингредиент которого, мескалин, играл важную роль в шаманских ритуалах многих племён Центральной Америки. Мескалин хорошо известен способностью вызывать яркие зрительные галлюцинации. Употребляя пейот в лаборатории вместе с ассистентом, Клювер заметил повторяющиеся геометрические формы в галлюцинациях, вызываемых мескалином, и разделил их на четыре типа, назвав их константами формы: туннели и воронки, спирали, решётки, куда входят соты и треугольники, и паутины.
В 1970-х математики Джек Коуэн и Бард Эрментраут использовали классификацию Клювера для создания теории, описывающей, что происходит в мозге, когда он заставляет нас поверить, что мы видим геометрические узоры. Их теорию в дальнейшем развивали другие учёные, включая и Пола Бреслова, профессора математической и вычислительной нейробиологии в недавно основанном Оксфордском Центре коллаборативной прикладной математики.
Откуда у коры головного мозга полоски *
Зрительная кора. Красным отмечена область V1
[* Отсылка к вьетнамской сказке «Откуда у тигра полоски» / прим. перев.]
Первой областью зрительной коры головного мозга, обрабатывающей изображения у людей и млекопитающих, является участок, известный, как V1. Экспериментальные свидетельства, например, изображения фМРТ, говорят о том, что узоры Клювера тоже в основном происходят из V1, а не появляются позже где-то в зрительной системе. Как и у остального мозга, у V1 сложная, морщинистая, складчатая структура — однако существует удивительно прямолинейный способ переводить то, что мы видим в нашем поле зрения в активность нейронов в V1. «Представьте, что мы разворачиваем V1, — говорит Бреслов. — Её можно представить себе как нервную ткань толщиной в несколько миллиметров, с различными слоями нейронов. В первом приближении нейроны по всей глубине коры ведут себя сходным образом, поэтому, если сплющить их, можно представить себе V1 как двумерный лист».
Объект или сцена зрительного мира проецируется в виде двумерного изображения на сетчатку каждого глаза, поэтому то, что мы видим, тоже можно расценивать как плоский лист: поле зрения. Каждую точку на этом листе можно обозначить двумя координатами, как точку на карте, или точку на плоской модели V1. Перемежающиеся светлые и тёмные участки, составляющие геометрические галлюцинации, вызываются перемежающимися участками высокой и низкой активности нейронов в V1 — участками, где нейроны активируются очень быстро, и участками, где всё наоборот.
Чтобы перевести зрительные узоры в активность нейронов, необходима координатная сетка — правило, по которому каждая точка поля зрения связана с точкой плоской модели V1. В 1970-х учёные, в том числе и Коуэн, сделали такую сетку на основе знаний об анатомии взаимодействия нейронов сетчатки с нейронами в V1. Для каждого светлого или тёмного участка поля зрения отображение определяет участок высокой или низкой активности нейронов в V1.
Как же это отображение сетчатки и коры преобразовывает геометрические узоры Клювера? Оказывается, что галлюцинации, вызывающие спирали, круги и лучи, исходящие из центра, соответствуют полоскам активности нейронов в V1, проходящими под заданными углами. Решётки типа сот или клеток соответствуют шестиугольным узорам активности в V1. Само по себе это, возможно, и не так интересно, однако есть один прецедент: именно полоски и шестиугольники учёные наблюдали при моделировании других примеров формирования узоров, к примеру, конвекции жидкостей, или, что более удивительно, появления пятен и полосок на шкурах животных. Математика, управляющая формированием этих узоров, была хорошо известна, и также предложила механизм моделирования работы визуальной коры.
От поля зрения к визуальной коре
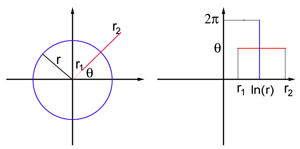
Представьте себе поле зрения в виде плоского листа с полярными координатами: каждая точка P определяется двумя числами, (r, θ), где r — расстояние до начала координат О, а θ — угол между отрезком OP и осью х. Начало отсчёта соответствует центру поля зрения. V1 также моделируется в виде плоского листа, но на этот раз обладающего декартовыми координатами (x, y). Точное координатное отображение поля зрения и плоской модели V1 слишком сложное для этой статьи, но для точек, достаточно далеко расположенных от центра поля зрения (то есть, для достаточно большого r) оно напоминает логарифмическое отображение:
Отображение транслирует круг радиуса r в поле зрения в прямой вертикальный отрезок с x = ln r, а луч, исходящий из начала координат О под углом θ, в прямой горизонтальный отрезок с y = θ
Откуда у леопарда пятна
Первая модель формирования узоров на шкурах животных восходит к Алану Тьюрингу, больше известному в качестве отца современной информатики и хакера из Блетчли-Парк, взламывавшего коды. Тьюринга интересовало, как такая пространственно гомогенная система, как однородный шар из клеток, которым является эмбрион животного, может создавать пространственно негомогенные, но статические узоры, такие, как полоски зебры.
Тьюринг предположил, что эти узоры появляются в результате реакционно-диффузного процесса. Представьте себе эмбрион животного, в коже которого живут два химических соединения. Одно из них — ингибитор, подавляющий выработку и себя, и другого химиката. Другой — катализатор, вызывающий выработку обоих веществ.
В начальный момент модели Тьюринга два химиката идеально балансируют друг друга — они находятся в равновесии, и их концентрация в различных точках на эмбрионе не меняется со временем. Теперь представьте, что по какой-то причине в одной точке концентрация катализатора немного увеличилась. Это небольшое возмущение приводит в движение всю систему. Повышенная местная концентрация катализатора означает, что там производится больше катализатора и ингибитора. Однако оба соединения также диффундируют по коже эмбриона, подавляя и катализируя их производство и в других местах.
К примеру, если ингибитор диффундирует быстрее катализатора, он быстро окружит точку возмущения и уменьшит концентрацию катализатора в ней. В итоге у нас получится участок с высокой концентрацией катализатора, окружённый высокой концентрацией ингибитора — иначе говоря, пятно катализатора на фоне ингибитора. В зависимости от скорости диффузии двух соединений, возможно, что такой пятнистый узор появится по всей коже эмбриона, и в итоге стабилизируется.
Тюринг записал систему дифференциальных уравнений, описывающих соревнование между двумя соединениями — можно позволить им развиваться во времени и посмотреть, появятся ли узоры. Эти уравнения зависят от параметров, описывающих скорость диффузии двух соединений: если правильно их подобрать, система в итоге стабилизируется, образовав определённый узор, который можно менять, меняя параметры. По ссылке представлен апплет на Java, в котором можно поиграться с параметрами и посмотреть на получающиеся узоры.
Уравнения животных узоров
Для простоты представим себе эмбрион в виде одномерной линии. В любой момент времени t и в любой точке х эмбриона концентрация катализатора (activator) и ингибитора (inhibitor) задаётся функциями A (x, t) и I (x, t). Они меняются со временем по следующим правилам:
Первый член справа каждого из уравнений описывает количество производства катализатора и ингибитора. Они являются функциями концентраций катализатора и ингибитора, поскольку оба влияют на скорость реакции.
Второй член справа каждого из уравнений — вторая производная, описывающая скорость изменения градиента катализатора и ингибитора. Они задают скорость диффузии.
Дополнительный член d в правой части второго уравнения — коэффициент диффузии, показывающий, насколько ингибитор диффундирует быстрее катализатора. Тьюринг показал, что превосходство в скорости ингибитора является критически важным параметром для процесса порождения пятен.
Узоры мозга
Активность нейронов в мозге — это не реакционно-диффузный процесс, однако у него есть аналогии с моделью Тьюринга. «Нейроны отправляют друг другу сигналы по каналам вывода данных под названием аксоны», — говорит Бреслов. Нейроны реагируют на сигналы друг друга, вот вам и реакция. «Сигналы распространяются так быстро, по сравнению с процессом формирования узоров, что их можно принять за мгновенные взаимодействия». Поэтому вместо диффузии, локального процесса, у нас есть мгновенное взаимодействие на расстоянии. Роли катализатора и ингибитора играют два разных класса нейронов. «Существуют возбуждающие нейроны — которые увеличивают вероятность у других нейронов стать активными — и есть подавляющие нейроны, уменьшающие эту вероятность, — говорит Бреслов. — Соревнование между двумя классами нейронов является аналогией механизму катализатора-ингибитора в модели Тьюринга».

Полосатые, шестиугольные и прямоугольные узоры нервной активности в V1, порождённые математической моделью
Вдохновившись аналогиями процессов Тьюринга, Коуэн и Эрментраут создали модель нервной активности в V1 при помощи набора уравнений, сформулированных Коуэном и Хью Уилсоном. Хотя уравнения оказались более сложными, чем у Тьюринга, вы всё равно можете сыграть в ту же самую игру, позволив системе развиваться со временем, и посмотреть, развиваются ли узоры нервной активности. «Можно обнаружить, что при определённых условиях если увеличить параметр, представляющий, например, действие наркотиков на кору, это приведёт к росту периодических узоров», — говорит Бреслов.
Модель Коуэна и Эрментраута предполагает, что геометрические галлюцинации появляются в результате нестабильности в V1: что-то, к примеру, присутствие наркотика, выводит нейросеть из сбалансированного состояния, запуская растущий, как снежный ком, процесс взаимодействия между возбуждающими и подавляющими нейронами, который затем стабилизируется в виде полосатых или шестиугольных узоров нервной активности в V1. Затем мы в поле зрения «наблюдаем» этот узор в виде геометрических структур, описанных Клювером.
Симметрии в мозге
На самом деле всё не так просто, как в модели Коуэна и Эрментраута, поскольку нейроны реагируют не только на светлые и тёмные изображения. По толщине V1 нейроны выстраиваются в колонки, известные, как гиперколонки, каждая из которых примерно реагирует на небольшой участок поля зрения. Но не все нейроны в гиперколонке одинаковы: кроме распознавания светлых и тёмных участок, каждый нейрон специализируется на распознавании локальных граней — линий, разделяющих светлые и тёмные участки в одной части изображения — определённой ориентации. Некоторые распознают горизонтальные грани, другие — вертикальные, иные — грани, расположенные под углом в 45°, и так далее. В каждой гиперколонке содержатся колонки нейронов всех предпочтительных ориентаций, поэтому гиперколонка может реагировать на грани всех ориентаций в определённом участке поля зрения. Именно состав гиперколонок и ориентационные предпочтения позволяют нам распознавать контуры, поверхности и текстуры зрительного мира.
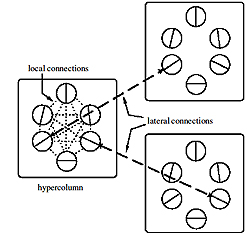
Связи в V1: нейроны в гиперколонке взаимодействуют с большей частью других нейронов. Но с нейронами в других гиперколонках они реагируют, только если колонки располагаются в направлении их ориентации, и у нейронов одно и то же ориентационное предпочтение.
В последние годы было собрано довольно много анатомических свидетельств того, как взаимодействуют между собой нейроны с различными ориентационными предпочтениями. Внутри своей геиперколонки нейроны взаимодействуют с большинством остальных нейронов, вне зависимости от их предпочтений. Но, что касается нейронов других гиперколонок, они действуют более избирательно, взаимодействуя только с нейронами сходных предпочтений, так, чтобы гарантировать нам возможность распознавать непрерывные контуры в зрительном мире.
Бреслов совместно с Коуэном, математиком Мартином Голубицким и другими учёными обобщил оригинальную модель Коуэна и Эрментраута, чтобы учесть эти новые анатомические свидетельства. Они вновь использовали плоскость в качестве основы модели V1: каждая гиперколонка представлена на плоскости точкой (x, y), и каждая точка (x, y) соответствует гиперколонке. Нейроны с заданным предпочтением к ориентации θ (где θ — это угол между 0 и π обозначаются положением гиперколонки (x, y) вместе с углом θ — то есть, они обозначаются тремя единицами информации, (x, y, θ). Поэтому в этой модели V1 — это не плоскость, а плоскость с полным набором ориентаций для каждой точки.
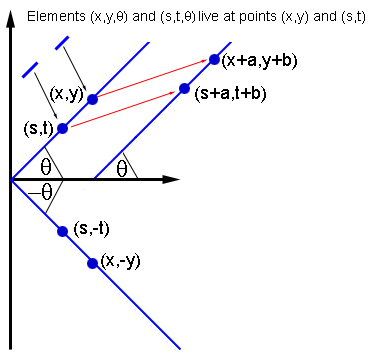
Если два элемента, (x, y, θ) и (s, t, θ) взаимодействуют, тогда взаимодействуют и другие элементы с той же ориентацией в точках (x+a, y+b) и (s+a, t+b), и элементы с ориентацией -θ в точках (x, -y) и (s, -t).
Чтобы соответствовать анатомическим свидетельствам, Бреслов с коллегами предположили, что нейрон, обозначенный точкой (x0, y0, θ0) взаимодействует со всеми другими нейронами в той же гиперколонке (x0, y0). Но с нейронами из других гиперколонок он взаимодействует, только если те лежат в его предпочтительной ориентации θ0: на плоскости нужно провести линию через точку (x0, y0) под углом θ0. Тогда нейроны, обозначенные точкой (x0, y0, θ0), взаимодействуют только с нейронами гиперколонок, лежащих на этой же линии, то есть, имеющих ту же предпочтительную ориентацию θ0.
Такая схема взаимодействий очень симметричная. К примеру, она не меняется при сдвиге плоскости в любом направлении на любое расстояние: если два элемента, (x0, y0, θ0) и (s0, t0, φ0), взаимодействуют, тогда элементы, получаемые сдвигом, (x0+a, y0+b, θ0) и (s0+a, t0+b, φ0) для некоторых a и b, взаимодействуют тем же образом. По тому же принципу схема инвариантна относительно вращений и отражений плоскости.

Галлюцинация с решётчатым туннелем, созданная математической моделью. Она сильно напоминает галлюцинации, возникающие при приёме марихуаны.
Бреслов с коллегами использовали обобщённую версию уравнений из оригинальной модели, чтобы позволить системе развиваться. В результате получилась модель, не только более точная в плане анатомии V1, но и способная порождать в поле зрения геометрические узоры, на которые оригинальная модель не была способна. Сюда входят решётчатые тоннели, соты и паутины, ориентация контуров которых характеризует их лучше, чем светлые и тёмные контрастные участки.
Более того, модель чувствительна к симметриям схем взаимодействия нейронов: математики показали, что именно эти симметрии порождают формирование периодических узоров нервной активности. Поэтому модель предполагает, что галлюцинации порождает расположение гиперколонок и предпочтений ориентаций, то есть, механизмы, помогающие нам распознавать грани, контуры, поверхности и текстуры зрительного мира. Именно когда эти механизмы теряют стабильность, например, в результате воздействия наркотика, появляются узоры активности, превращающиеся в зрительные галлюцинации.
За пределами галлюцинаций
Модель Бреслова не только позволяет проникнуть в суть механизмов, порождающих зрительные галлюцинации, но и даёт подсказки по поводу архитектуры мозга в более широком смысле. Вместе со своей женой, нейробиологом-экспериментатором, Бреслов изучал контуры соединений гиперколонок при нормальном зрении, чтобы понять, как обрабатываются зрительные изображения. «Люди привыкли считать, что нейроны в V1 просто определяют местные грани, и что нужно выходить на более высокие уровни мозга, чтобы собрать эти грани и распознать более сложные вещи типа контуров и поверхностей. Но из нашей с супругой работы видно, что эти структуры в V1 на самом деле позволяют зрительной коре на раннем этапе распознать контуры и проводить более глобальную обработку. Считалось, что мы обрабатываем всё более и более сложные аспекты изображения, поднимаясь выше по иерархии мозга. Теперь же стало понятно, что между верхней и нижней частями коры идёт активная обратная связь. Это не простой иерархический процесс, а невероятно сложная и активная система, на понимание которой уйдут многие годы».
Среди практических применений этой работы находится и компьютерное зрение — специалисты по информатике уже выстраивают структуры с внутренними связями, с которыми Бреслов с коллегами игрались при построении моделей, чтобы научить компьютеры определять контуры и текстуры. Если проявить немного фантазии, можно представить, что это исследование когда-нибудь сможет помочь восстановить зрение людям с нарушениями. «Вопрос в том, можно ли как-то стимулировать часть визуальной коры, в обход глаза, и использовать это для ориентации слепого, — говорит Бреслов. — Если понять, как устроена кора и как она реагирует на стимуляцию, возможно, тогда можно будет изобрести лучший метод её правильной стимуляции».
Есть даже и такие области применения, которые вовсе не связаны с мозгом. Бреслов применил идеи, полученные благодаря работе, к другим ситуациям, в которых объекты расположены в пространстве с определённой ориентацией, например, к фибробластам из тканей человека и животных. Он показал, что при определённых условиях эти взаимодействующие между собой клетки и молекулы могут выстраиваться и порождать узоры, аналогичные тем, что появляются в V1.
Люди рассказывали о том, что видят галлюцинации, с начала времён, и практически во всех культурах — изображения галлюцинаций можно даже найти в петроглифах и наскальных рисунках. В традициях шаманов всего мира к ним относятся, как сообщениям из мира духов. Мало какие современные нейробиологи согласятся с причастностью духов к этому, но в качестве вестников скрытого мира — на этот раз, скрытого мира нашего мозга — эти галлюцинации не утратили своих возможностей.
