[Из песочницы] Neurotic Bikes: генезис
На днях Youtube посчитал, что мне покажется интересным видео с названием «AI Learns to play Hill Climb Racing». Забавно, ведь за пару минут до этого я закоммитил очередные изменения в проект, где мы с коллегами в перерывах между работой и работой решаем именно эту задачу. Никакого «AI» в том видео, правда, не обнаружилось — автор поразвлекал публику баловством с Box2D и на том успокоился. Тем не менее, предлагаю считать этот факт убедительным доказательством актуальности темы и разобрать устройство нашей погремушки.
Коротко о задаче: транспортное средство — в нашем случае это то ли Чужой, то ли швейная машинка «Зингеръ» на колесах, назовем его просто «агент» — должно проехать по наперлинным одноименным шумом барханам от старта до финиша. Вот так выглядит агент в своей песочнице:

Агент, коснувшийся спиной трека или не демонстрирующий должного рвения в продвижении к цели, снимается с трассы.
Решать задачу будем с использованием нейронных сетей, но оптимизируемых генетическим алгоритмом (ГА) — такой процесс называют нейроэволюцией. Мы воспользовались методом NEAT (NeuroEvolution of Augmenting Topologies), изобретенным Кеннетом Стенли и Ристо Мииккулайненом в начале века [1]: во-первых, он хорошо зарекомендовал себя в важных для народного хозяйства проблемах, во-вторых, к началу работы над проектом у нас уже был свой фреймворк, реализующий NEAT. Так что, честно говоря, метод решения мы не выбирали — скорее, выбирали задачу, где можно погонять уже готовое.
На рисунке изображена примерная схема работы генетических алгоритмов:
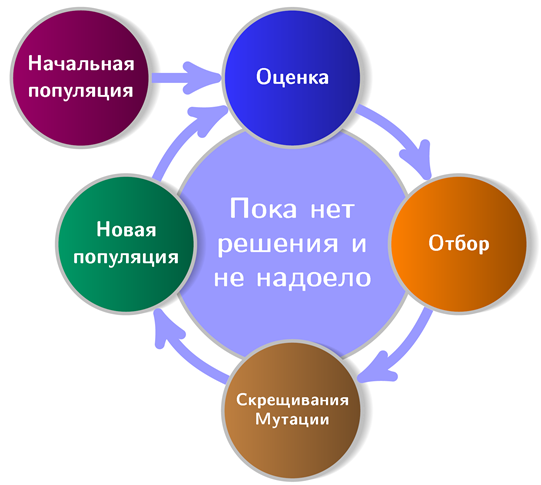
Видно, что любой приличный ГА стартует с начальной популяции (популяция — набор потенциальных решений). Займемся ее созданием и заодно познакомимся с первым принципом NEAT. Согласно этому принципу все агенты стартовой популяции должны иметь простейшую, «минимальную» топологию нейронной сети. При чем тут топология? Дело в том, что в NEAT вместе с оптимизацией весов связей эволюционирует и архитектура сети. Это, между прочим, избавляет от необходимости ее проектирования под задачу. Идти от простых архитектур к сложным не просто логично, но и практично (меньше пространство поиска), поэтому и начинать надо с минимальной из возможных топологий — примерно так рассуждали авторы метода.
Для нашего и всех похожих случаев эта минимальная топология выводится из следующих соображений. Чтобы делать что-то осмысленное агенту нужно:
- иметь данные об окружающей среде и своем состоянии,
- обрабатывать эту информацию,
- взаимодействовать со своим миром.
Первую роль выполняют сенсоры — нейроны входного слоя, на которые будем подавать полезную агенту информацию. Нейроны выходного слоя будут обрабатывать данные с сенсоров. За взаимодействие со средой отвечают актуаторы — устройства, выполняющие механические действия в ответ на сигнал со «своего» нейрона выходного слоя. Общий принцип построения начальной конфигурации, таким образом, следующий: определяемся с сенсорами и актуаторами, заводим по одному нейрону на актуатор, все сенсоры и еще один специальный нейрон — нейрон смещения (bias, о нем — ниже) соединяем связями со случайными весами со всеми нейронами выходного слоя. Как-то так:
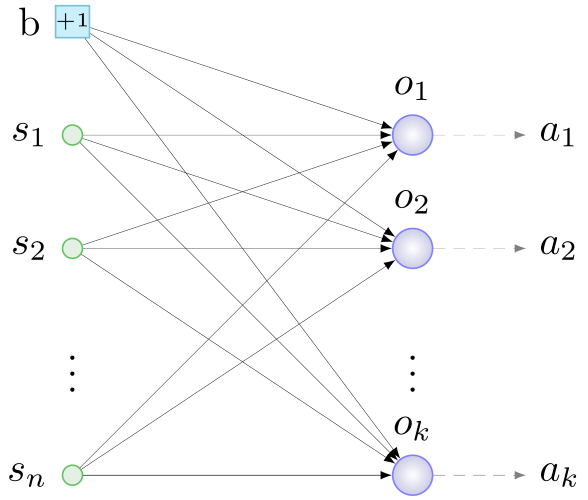
b — bias, s — сенсоры, o — нейроны выходного слоя, a — актуаторы, n — кол-во сенсоров, k — кол-во актуаторов
А вот так выглядит минимальная НС для нашей задачи:
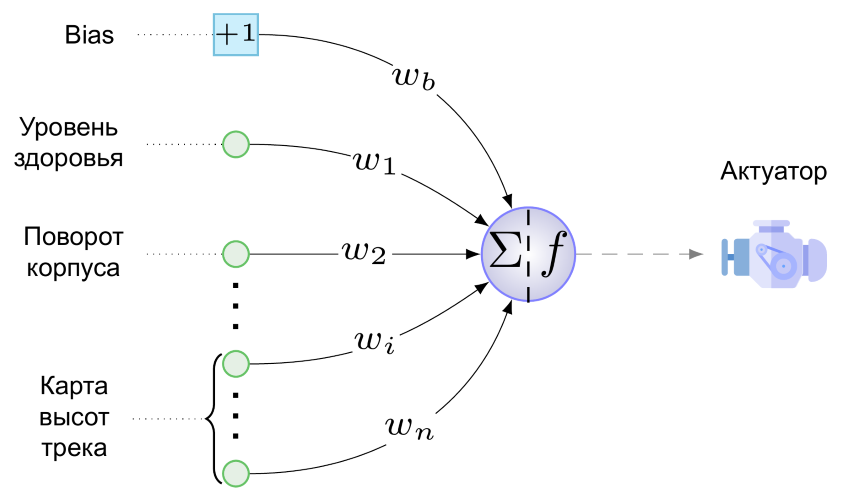
У нас всего один актуатор — это двигатель нашего колесного создания. Стрелять, прыгать и играть на дуде оно пока не умеет. На двигатель с единственного нейрона выходного слоя (его и слоем-то называть стыдновато) подается вот такое значение:
Здесь wb — значение веса связи, идущей от bias«а к выходному нейрону, умноженное на то, что «производит» всякий bias, т.е. +1, si — отнормированное к диапазону [0,1] значение на i-том сенсоре, wi — значение веса связи от i-го сенсора до выходного нейрона, а f — функция активации.
В качестве функции активации мы используем вот эту фантазию на тему softsign:
— она продемонстрировала лучшую производительность в тестах одного небезызвестного в узких кругах нейроэволюциониста [2]. А сравнивать приятную глазу мягкость изгибов и симметричность графика этой функции с угловато-кособоким Leaky ReLU вообще смысла нет:

На этом рисунке показана реакция агента на разные значения функции активации. При близких к единице значениях двигатель крутит колеса по часовой стрелке, разгоняя агента вперед и сильно отклоняя корпус назад, так что слабоумные, но отважные быстро опрокидываются на спину и погибают. При значениях, близких к 0 — все наоборот, а при значении 0.5 мотор агента не работает.
На этом же рисунке показана роль нейрона смещения — вес связи, идущей от него к нейрону выходного слоя, отвечает, как следует из (1), за величину и направление смещения f (x) вдоль оси абсцисс. Пунктиром на рисунке изображен график функции активации при wb=-1. Получается, что даже при отсутствии сигнала на сенсорах, агент с такой связью будет довольно резво ехать назад: f (x)=f (-1+0)≈0.083<0.5. Вообще, сдвиг значений функции по горизонтали позволяет bias-ной связи тонко (ну или толсто – в зависимости от веса) настроить реакцию двигателя на все значения сенсоров и веса их связей разом. Вроде и новое измерение добавили в пространство поиска («правильное»-то значение для wb придется поискать), но польза в виде дополнительной степени свободы от возможности таких смещений перевешивает.
Отлично, мы представили нейронные сети агентов будущей начальной популяции. Но NEAT — генетический алгоритм, и работает он с генотипами — структурами, из которых образуются сети или, если говорить более общо, фенотипы в процессе декодирования. Раз уж начали с фенотипа, сделаем все задом наперед: попробуем закодировать представленную выше сеть в генотипе. Здесь не обойтись без второго принципа NEAT, основная суть которого состоит в следующем: в генотипе помимо структуры нейронной сети и весов ее связей сохраняется информация об истории происхождения всех ее элементов. За исключением этого исторического аспекта фенотип кодируется в генотипе почти «один к одному», поэтому иллюстрировать второй принцип пока будем фрагментами нейронных сетей.
Значение этого принципа переоценить сложно — агентам он обеспечивает возможность полового размножения. Тема довольно деликатная, поэтому рассмотрим вначале размножение бесполое. Происходит оно так: делается копия всех генов агента, над ними производится одно из нескольких типов изменений — мутаций. В нашей версии NEAT возможны следующие мутации:
- изменение веса связи,
- удаление связи,
- добавление связи,
- вставка нейрона.
Первые три типа мутаций просты и понятны без дополнительных разъяснений. Вставка нейрона показана на рисунке ниже, она происходит всегда на место существующей связи, связь при этом удаляется, а на ее месте появляются две новые:
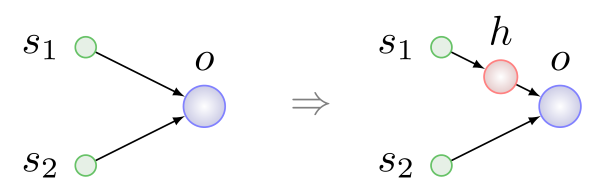
Здесь h — скрытый (hidden) нейрон.
В половом размножении или скрещивании участвуют два агента — родители, а в результате появляется третий — ребенок. В процессе образования генотипа ребенка происходит обмен, скажем так, одинаковыми по смыслу генами или группами генов родителей. Второй принцип как раз и нужен для поиска генов с одинаковым смыслом.
Представим, что мы хотим скрестить агентов с генотипами, претерпевшими разные серии мутаций из рассмотренного выше перечня:
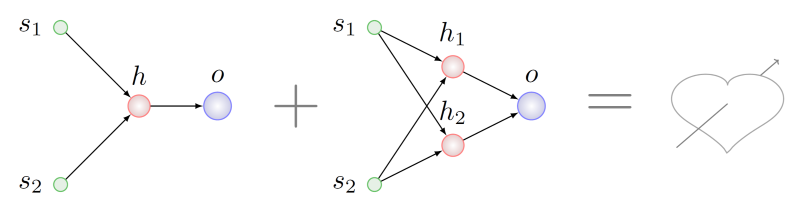
Кажется логичным поискать какие-то общие с точки зрения топологии фрагменты у обоих родителей и взять по кусочку из этих фрагментов для генотипа будущего ребенка. Сделать это будет сложновато, даже NP-сложновато в общем случае, но, положим, мы справились. В этом случае обнаружим, что в родителе справа присутствуют два подграфа, изоморфных графу левого родителя. На рисунке ниже дуги этих подграфов выделены разными цветами:
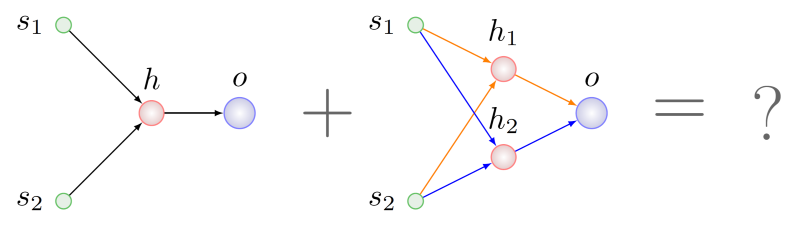
Какой из них выбрать для рекомбинации с генами левого родителя?
Обратимся к истории возникновения этих генотипов:
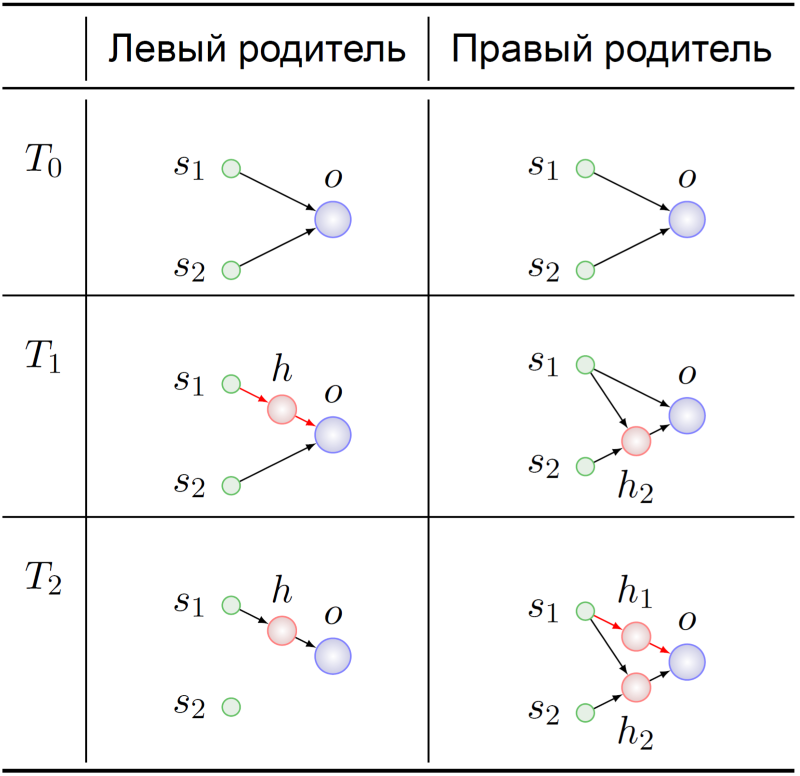
Оба предка агентов-родителей стартовали, как и положено, с минимальной НС (T0). Их геномы как-то там мутировали, а в момент времени T1 в предке левого родителя произошла вставка скрытого нейрона в связь s1 → o. В этот драматический момент гены, кодирующие связи s1 → h и h → o, обретают свой смысл в предке левого родителя: замещение связи s1 → o.
Точно такой же смысл обрели гены s1 → h1 и h1 → o в генотипе правого родителя в момент времени T2. Дальнейшие судьбы предков нас не особо интересуют — мы ведь уже знаем, что с чем можно перемешать:
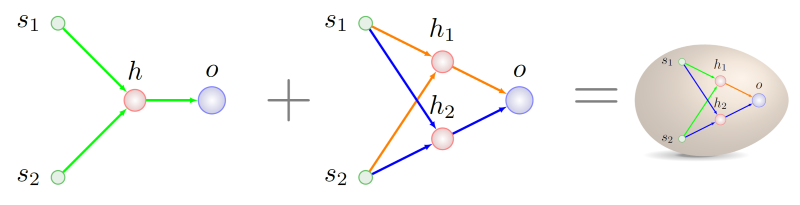
Как правильно писать генетическую историю, можно будет разобрать в следующий раз, тем более что у нас имеются кой-какие мелкие находки в этой области, они связаны с адаптацией оригинальной методики под устойчивую схему репродукции.
Пора закругляться. Статья началась с Youtube — им ее и завершим. В ранней версии симулятора коллега, писавший код генерации трека, закончил его ничем, бездонной пропастью. Реакцию нейронной сети, долгое время эволюционировавшей в условиях присутствия земной тверди под колесами, на такой дизайн ее маленькой вселенной можно, пожалуй, обозвать «разрывом шаблона»:
С обширной коллекцией других анекдотических историй из жизни кибернатуралистов можно ознакомиться в [3].
Источники
[1] K.O. Stanley and R. Miikkulainen, «Evolving Neural Networks through Augmenting Topologies» Evolutionary Computation, vol. 10, no. 2, pp. 99–127, 2002.
[2] C. Green, «A Review of Activation Functions in SharpNEAT,» 19 June 2017.
[3] J. Lehman et al, «The Surprising Creativity of Digital Evolution: A Collection of Anecdotes from the Evolutionary Computation and Artificial Life Research Communities,» arXiv: Neural and Evolutionary Computing, 2018.
