[Перевод] Простое объяснение симуляции жидкости в реальном времени

Эта статья представляет собой простой и интуитивно понятный разбор симуляции жидкостей для программистов и технических художников. Вместо сложных математических выражений я постараюсь дать вам простое геометрическое понимание физики жидкостей. Реализация выполнена на вычислительных шейдерах Unity 3D, однако общие идеи не привязаны к конкретным технологиям.
Код проекта можно найти на моём Github: https://github.com/IRCSS/Compute-Shaders-Fluid-Dynamic-
Ресурсы, посвящённые симуляции жидкостей, могут быть очень пугающими. Помню, что когда я впервые прочитал статью о ней и увидел уравнения Навье-Стокса, то был в ужасе. Со временем я понял, что сама тема совершенно не сложна. На самом деле, если бы вам дали задачу написать собственный симулятор жидкостей, то вы, вероятно, написали бы что-то подобное на основании интуитивного понимания работы жидкостей. Если, посмотрев на уравнения Навье-Стокса, вы подумали «ага, понятно», то вы, возможно, быстрее бы реализовали симуляцию жидкости, прочитав работы, перечисленные в конце этой статьи. Я же попытаюсь не использовать сжатое выражение и объяснять всё как можно медленнее.
Краткое описание поста. В начале мы забудем о существовании уравнения Навье-Стокса и попытаемся придумать собственную реализацию симуляции жидкости. Помните, что эта первая реализация будет наивной, имеющей недостатки. Но мы всё равно её создадим, чтобы после увеличения сложности нашей реализации для устранения этих недостатков вы поняли, почему они возникли, смогли смотреть сквозь эту сложность и видеть фундаментальную реализацию. Также не забывайте о том, что многие объяснения, которые я привожу в статье, необходимы для описания явления простыми словами, чтобы у вас появилось интуитивное понимание. Эти формулировки никогда не будут ни самыми точными, ни самыми эффективными способами описания различных элементов, но их более чем достаточно для написания реалистичного эффекта.
Свойства жидкостей
Для начала давайте изучим материалы из реального мира. Налейте себе стакан воды, поэкспериментируйте с ним, посмотрите, какие визуальные характеристики воды вам нужно имитировать, чтобы она воспринималась как правдоподобный водоём. Капните туда каплю соевого соуса, и понаблюдайте, как она перемещается, когда вы двигаете пальцем под водой или она остаётся неподвижной.
Вы можете заметить три следующих аспекта:
Во-первых, при попадании капли чернил или соевого соуса, даже если вы не трясёте стакан и не перемешиваете воду, соевый соус всё равно естественным образом распределяется и диффундирует, пока не окажется равномерно распределён в воде.
Во-вторых, вы можете взболтать воду. Если засунуть палец в воду и подвигать им, то вы создадите серию движений /векторов скоростей, которые продолжат существование и влияние друг на друга даже после извлечения пальца из воды. То есть сила, прикладываемая к водоёму, создаёт некое движение в воде. В эту систему можно добавлять компоненты, например, силу или чернила. Также обратите внимание на то, что векторы скоростей тоже спустя какое-то время «диффундируют» и распространяются.
В-третьих, краска, чернила или соевый соус будет перемещаться по водоёму в зависимости от направления приложения силы к поверхности. То есть водоём обладает векторами скорости, а вещества внутри него перемещаются/подвергаются адвекции из-за движения молекул воды в этой области.
Теперь остановитесь и подумайте о том, как можно закодировать вышеперечисленные элементы. Помните о том, что в заданный момент времени различные части стакана с водой имеют разные плотности соевого соуса и разные векторы скорости, которые меняются со временем.
Подобные задачи обычно решаются двумя способами. Первый — симуляция явления при помощи частиц, заменяющих массив молекул воды. Второй — сетка симуляции, в которой каждая ячейка представляет собой состояние этой части водоёма. Состояние этой ячейки зависит от различных полей (векторов скоростей, температуры, количества краски и т.д.), которые меняются с учётом движения в системе. Разумеется, можно использовать сочетание обоих способов. В этой статье я буду использовать сетку.
Кроме того, я буду моделировать всё в 2D, потому что так проще для объяснения. Поняв базовую идею, будет несложно перенести её в 3D.
У нас есть 2D-сетка, в которой каждая ячейка представляет собой состояние жидкости в этой части. Ячейки пространственно ограничены, то есть они относятся только к конкретной части воды, а не привязаны к молекулам воды. Молекулы перемещаются через эти ячейки и переносят с собой такие величины, как краска и их собственный вектор скорости. Наша задача — вычислять состояние жидкости для каждой из этих ячеек в каждом кадре. То есть в каждом кадре симуляция движется вперёд на основании результатов предыдущего кадра и тех событий, которые в нём произошли.
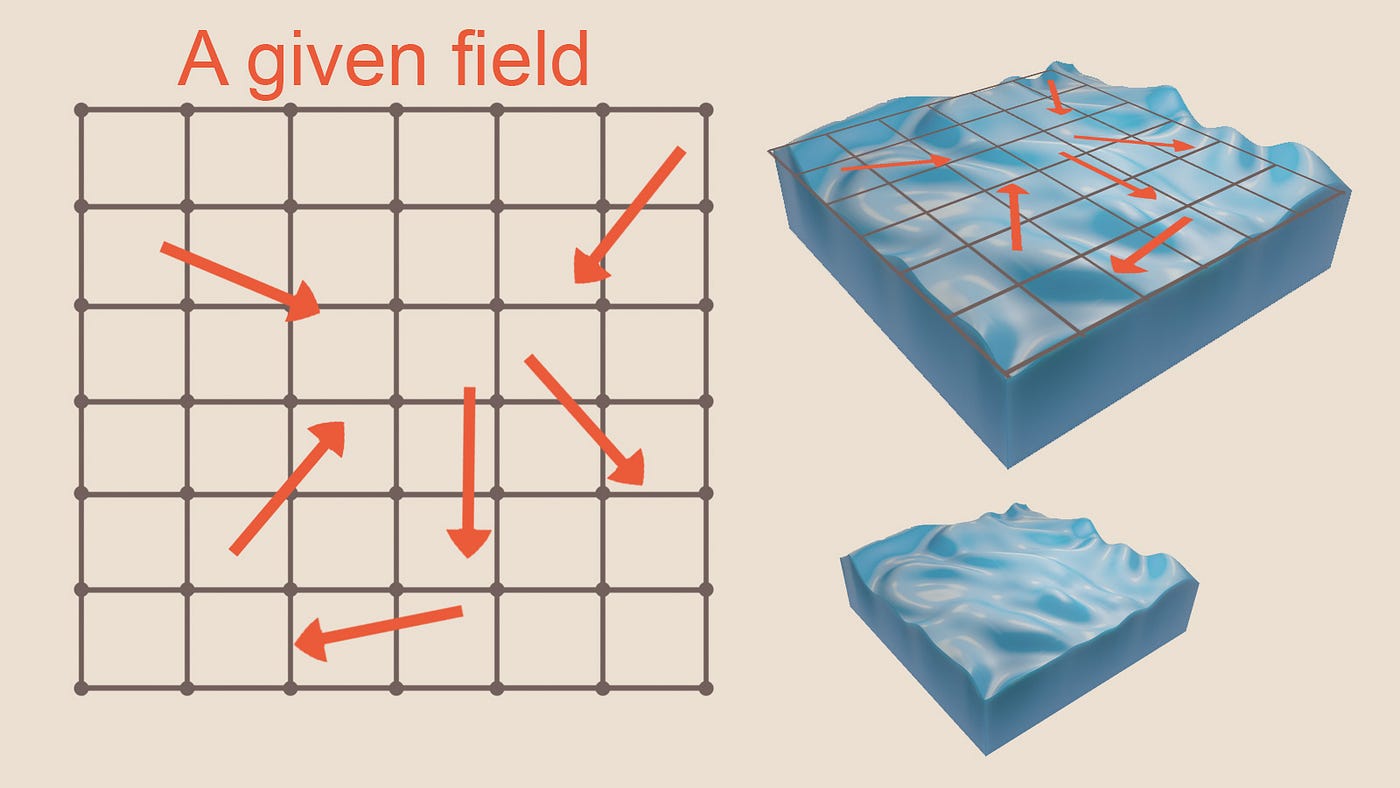
Рисунок 1 — Задаём водоём как последовательность полей в ячейке
На основании наших трёх наблюдений мы найдём величину интересующего нас поля для каждой ячейки по следующим трём факторам:
Количества чего-то в этой ячейке = что диффундировало из соседних ячеек + что было принесено откуда-то ещё из-за движения воды + что было добавлено в ячейку пользователем в этом кадре
Иными словами:
FluidStateForFieldX = Diffusion_of_X + Advection_of_X + X_Added_by_the_user
Теперь нам достаточно всего лишь запрограммировать каждый из этих факторов в каждом кадре и применить их к каждому полю в нашей жидкости, обновляя поля для следующего кадра и выполняя рендеринг результатов.
Наивная реализация, диффузия
Как говорилось выше, капля соуса диффундирует и распространяется от точки, в которую она была добавлена в водоём. Поразмыслив, можно понять, что это простой процесс обмена. В каждом кадре для любой ячейки краска перетекает в соседние ячейки, а краска из соседней ячейки перетекает в текущую ячейку. Со временем краска растечётся по всей сетке и вся сетка достигнет однородного значения количества имеющейся в ней краски, как в видео выше.
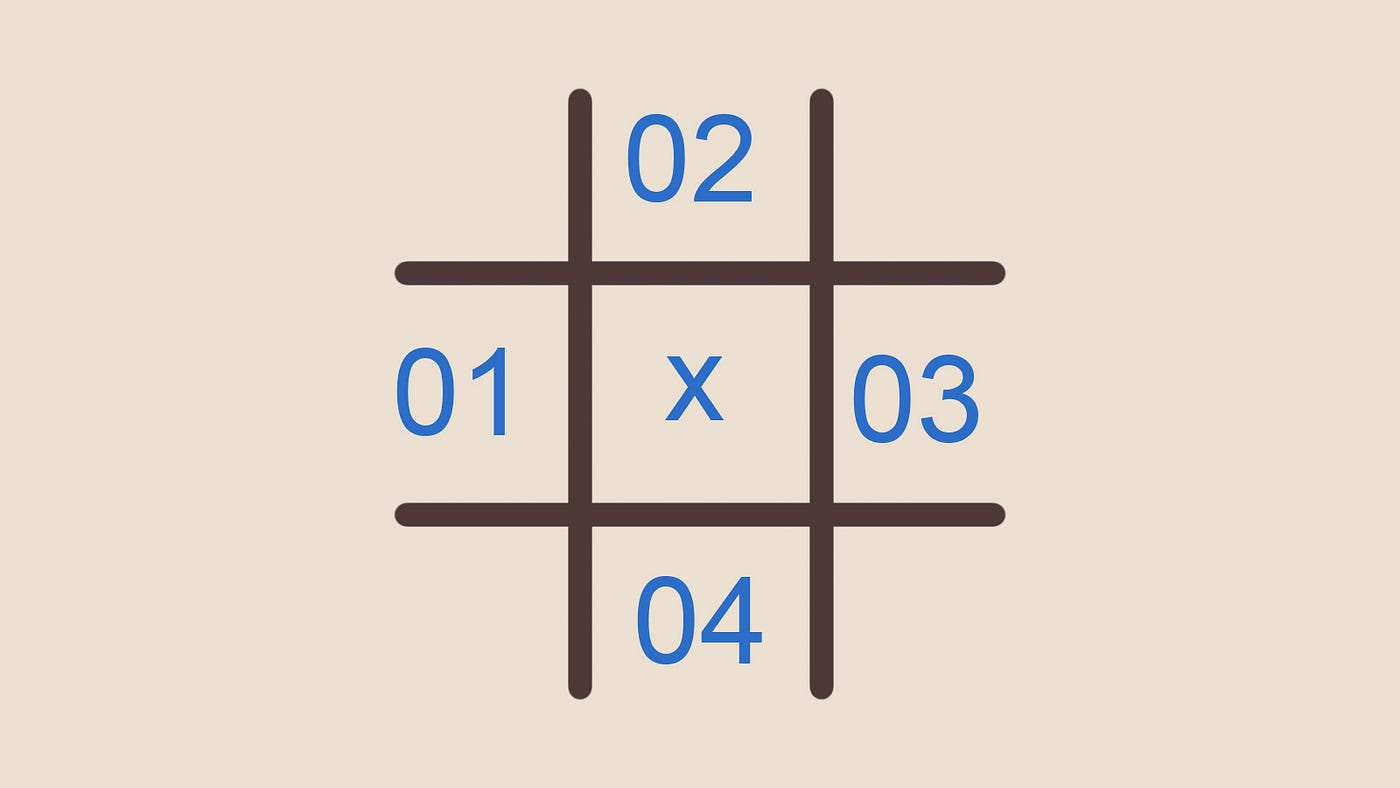
Рисунок 2 — Сетка A; поле помеченное крестом — текущая обрабатываемая ячейка
Пусть дана сетка (A). Количество краски в этом кадре d при количестве краски в предыдущем кадре d0 вычисляется как:
d_X= d0_X + diffusionFactor * deltaTime (d0_01 + d0_02+ d0_03 + d0_04 -4*d0_X)
Логика в том, что каждая ячейка отдаёт 4 порции имеющейся у неё краски и получает одну порцию из каждой соседней ячейки; эквивалентным утверждением будет то, что для каждой четверти получаемой ячейкой краски она отдаёт одну. Помните, что фактор диффузии (заданная нами постоянная) и дельта времени делают диффундируемую часть довольно небольшой, так что на самом деле ячейка не отдаёт 4 раза своё количество краски (что было бы физически невозможно), а числа — это просто соотношения.
Эта система достаточно проста для реализации на GPU или CPU.
Наивная реализация, адвекция
Адвекцию тоже можно реализовать очень легко. В каждом кадре нам нужно считать величину вектора скорости рассматриваемой ячейки и учесть, что молекулы в этой ячейке будут двигаться со скоростью в направлении вектора скорости, перенося с собой любое вещество в воде. Поэтому мы можем считывать этот вектор скорости, считывать плотность поля, которое нас интересует в этой ячейке, и перемещать её по сетке с этой скоростью туда, где оно окажется, учитывая дельту времени между этим кадром и следующим моментом, когда мы будем рассматривать поле, то есть следующим кадром. Этот способ проецирует поле в будущее состояние при помощи вектора скорости.
Field_amount_for_target[cellPosition + current_cell_velocity * timestep] = field_amount_for_current_cell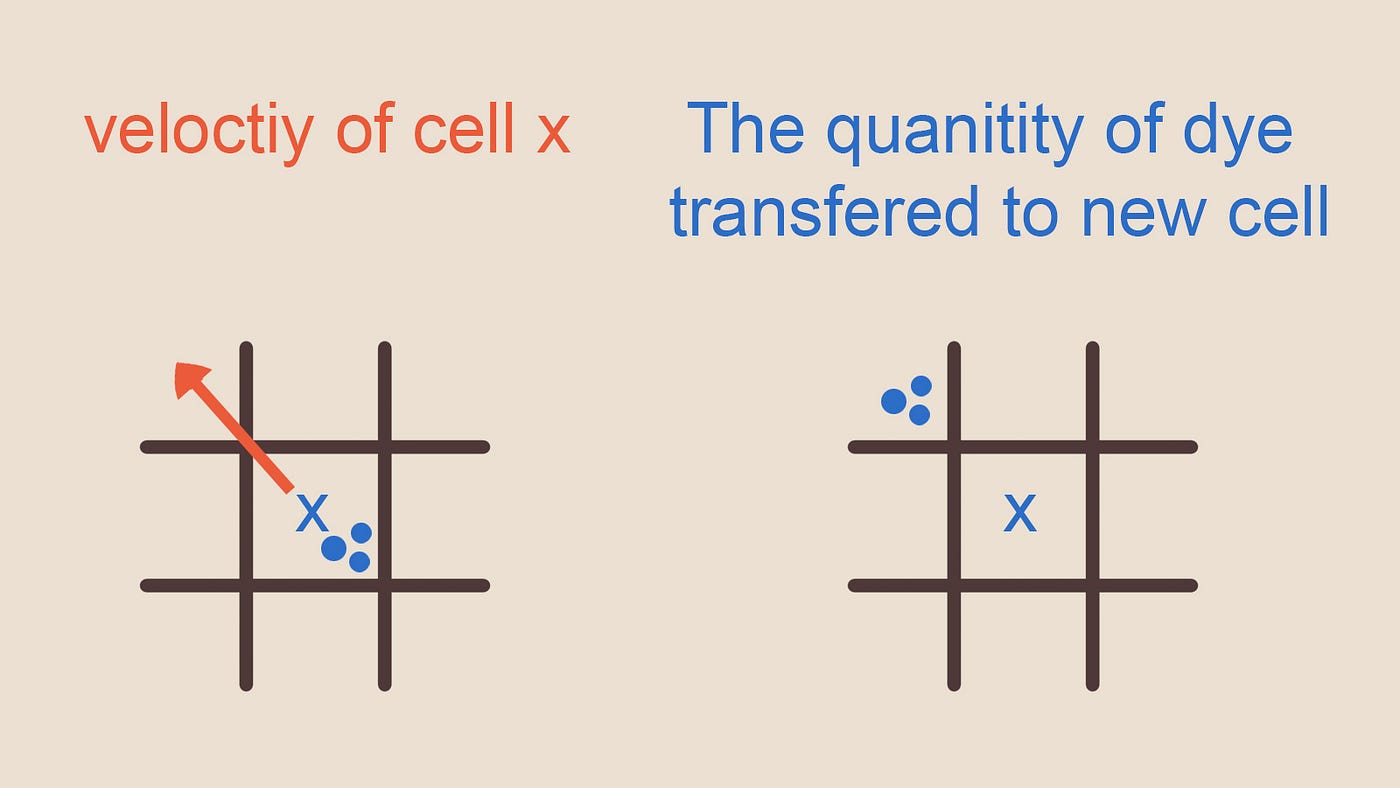
Рисунок 3 — Адвекция
Реализация, пользовательский ввод
Это единственная часть нашей первой реализации, которая останется окончательной. Просто вычислим величину пользовательского ввода для каждой рассматриваемой ячейки и прибавим её к значению поля в этой ячейке. Способы вычисления могут быть очень разными, например, через ввод мышью, через постоянный поток ввода, шум, изображение и т.п.
Amount_of_field_X += user_input_for_this_cell
Если реализовать описанную выше систему, то мы обнаружим нечто, напоминающее поведение жидкости (например, часть с диффузией будет походить на попавшую на бумагу акварельную краску), и можно будет даже без особых проблем реализовать систему на CPU, если она останется однопоточной. Однако текущая реализация имеет три важных изъяна: жидкость сжимаема, она не подходит для многопоточной обработки и нестабильна при больших шагах времени.
Изъян первый — сжимаемая жидкость?
Одной из ключевых характеристик жидкостей являются те красивые завитки, возникающие при движении пальца под водой. Вопрос в том, как возникают эти завитки и почему их нет в нашей симуляции?
Рассмотрим следующий сценарий. В показанной ниже сетке все соседние ячейки имеют векторы скорости, направленные в одну ячейку. Если все эти молекулы перенесутся в следующем кадре в эту ячейку, то как они там поместятся? Они сожмутся?

Рисунок 4 — Сжимающиеся молекулы воды
Или рассмотрим ещё один сценарий с векторами скоростей, непрерывно указывающим в стороны от центральной ячейки. Откуда будут браться эти молекулы со временем, материя будет создаваться из ничего?

Рисунок 5 — Вещество, постоянно переносимое из точки
Описанные выше сценарии возникают из-за того, что отсутствует в нашей симуляции, а именно невозможности сжатия жидкостей (или, по крайней мере, это достаточно хорошее допущение для реализации правдоподобной симуляции жидкости). В имеющейся симуляции мы никак не компенсируем того, что нельзя бесконечно выталкивать воду в сегмент пространства без каких-либо последствий.
Именно из-за несжимаемости жидкостей в водоёмах возникают эти красивые завитки. Интуитивно можно рассуждать об этом так: если мы двигаем что-то вперёд, но это нельзя сдвинуть вперёд, то оно должно двигаться в стороны, что создаёт завитки. Мы устраним эту проблему при помощи проецирования, которое рассмотрим сразу после двух других изъянов.
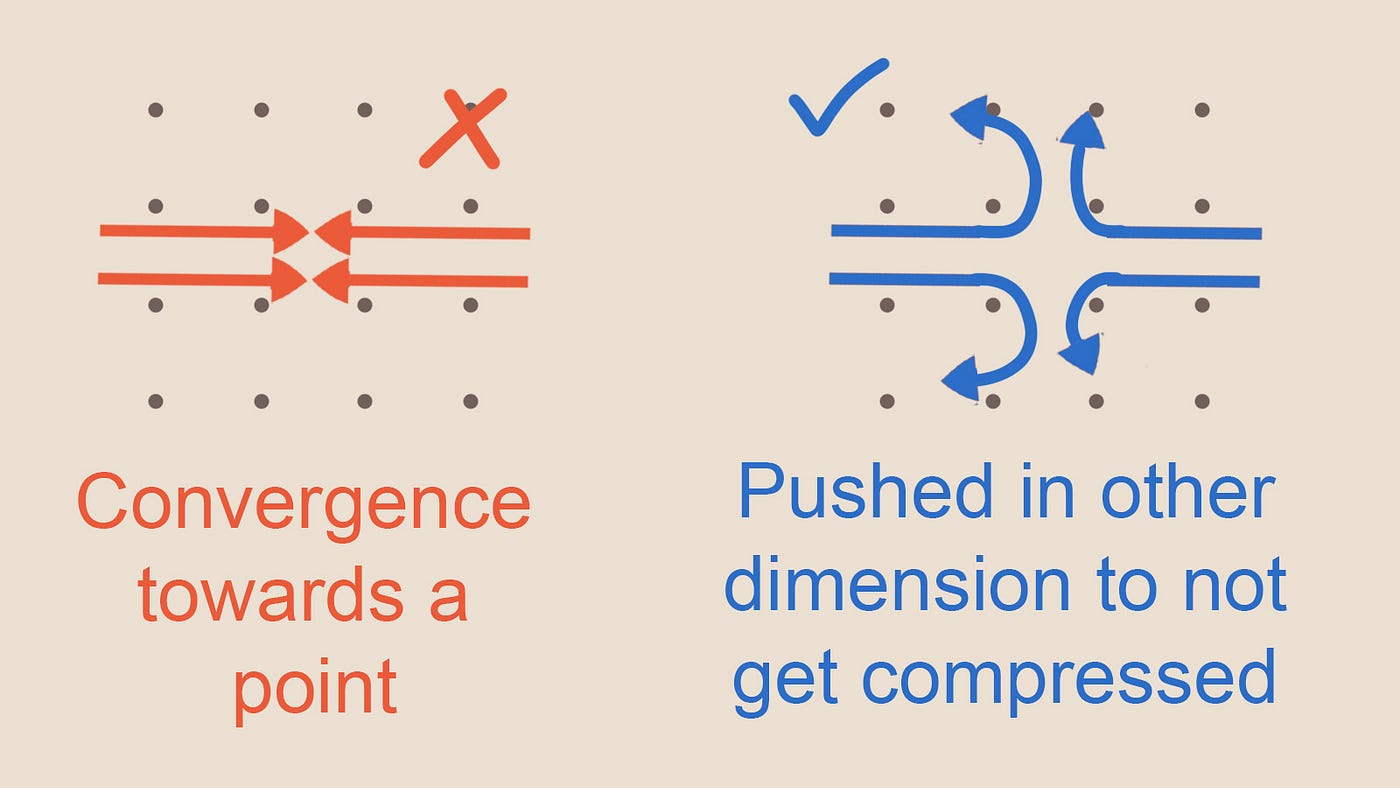
Рисунок 6 — Жидкость движется туда, куда может, потому что она несжимаема
Изъян второй: неудобство для реализации на GPU
Давайте снова взглянем на вычисление адвекции. Каждая ячейка смотрит на вектор скорости, который имеет в данный момент, а затем распространяет величину какого-то из полей на основании этой скорости в то место, которого достигнет вектор скорости после шага времени. Иными словами, каждая ячейка выполняет запись не в собственную память, а в некое неизвестное место. Такой тип паттерна доступа называется scatter operation.
Если задуматься о многопоточности (на CPU или GPU), то у нас возникнет проблема. Если мы привяжем каждый поток к ячейке, то потоки будут выполнять запись в участки памяти, в которые потенциально должны выполнять запись и другие потоки. Это создаёт условие гонки.
В идеале нам нужна схема, при которой поток привязывается к ячейке и каждый поток выполняет запись в память ячейки, которая ему назначена, а считывание выполняет только из соседних ячеек. Это будет примером gather operation. GPU отлично справляются с gather operations.
Изъян третий: нестабильность
Этот изъян сложно объяснить и полное его рассмотрение находится вне рамок нашей статьи.
При вычислении адвекции и диффузии полученным нами способом мы задаём значение вектора скорости в будущем на основании его значения в прошлом (предыдущем кадре), шага времени, прошедшего между прошлым и настоящим (дельты времени кадра), и величины изменения значения в предыдущем кадре (определяемой на основании некой функции, выведенной нами из справочных материалов и дедукции). Значение в любой момент времени явным образом задаётся через эти факторы.
Проблема такого подхода в том, что если дельта времени или в случае диффузии — дельта времени и/или коэффициент диффузии становятся слишком большими (например, больше, чем размер ячеек при адвекции или объёма краски при диффузии) из-за каких-то членов в нашей формулировке адвекции/диффузии, то решение становится нестабильным и колеблющимся (переключающимся между положительным и отрицательным или меньшим и большим ответом в каждом кадре) и рано или поздно «взрывается» до очень больших чисел. То есть стабильность здесь вопрос не точности результата, а того, сойдётся ли со временем результат к стабильному значению.
Давайте построим простой теоретический пример. Мы итеративно развиваем состояние нашей симуляции, в каждом кадре обновляя значения. Это в лучшем случае является приблизительной оценкой. Представьте, что вам нужно воссоздать функцию (A) итеративно, в текущий момент времени вы берёте предыдущее значение функции в предыдущем кадре (которое мы знаем) и прибавляете наклон функции в этой точке, чтобы продвинуть наше примерную оценку функции вперёд. Однако этот наклон является одномоментным и при больших скачках во времени мы полностью выйдем за пределы функции, как это показано ниже. Обратите внимание, что даже при небольшой дельте времени синие точки (наше аппроксимированное решение задачи) не лежат чётко на красной линии. В нашей аппроксимации всегда есть некоторая погрешность.
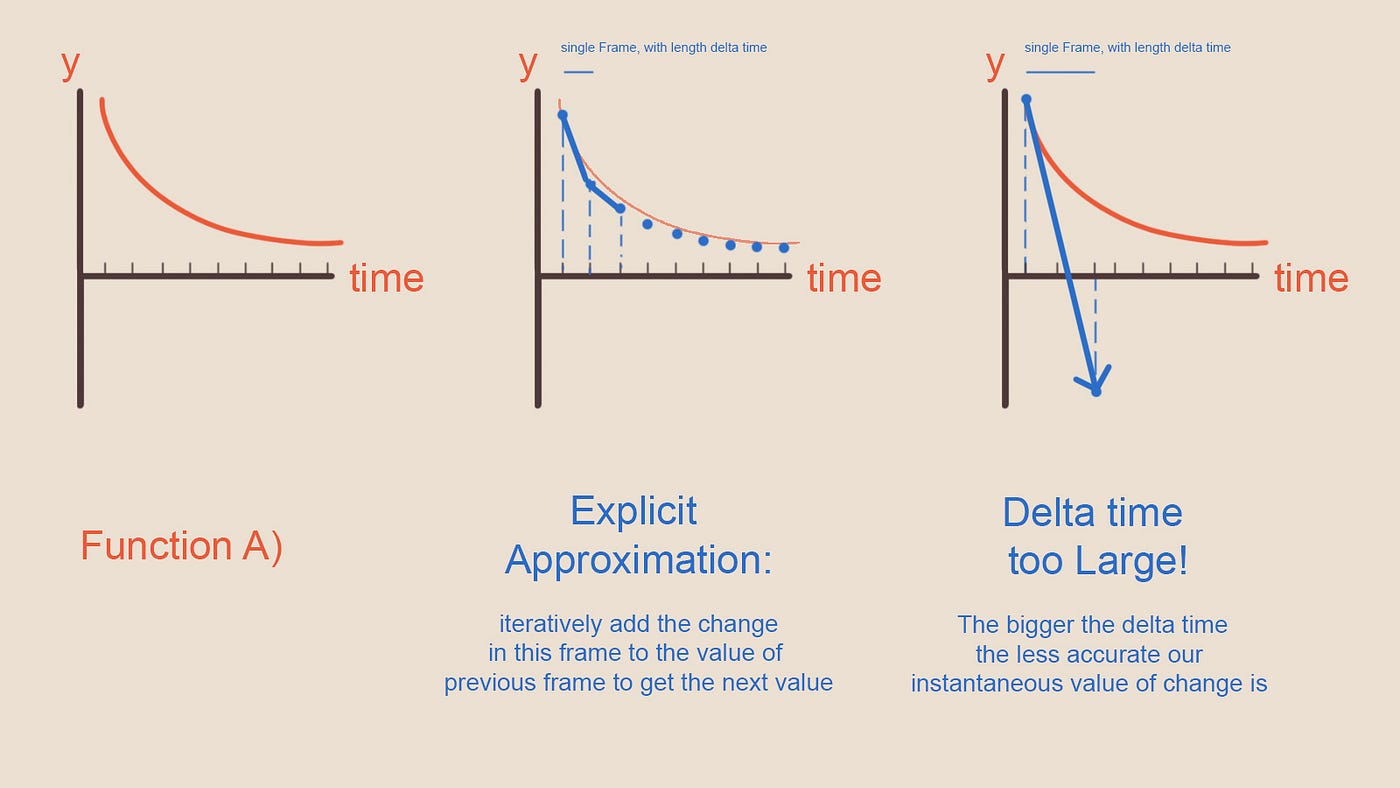
Рисунок 7 — Слишком большая дельта времени приводит к взрыву значений. Каждый шаг имеет локальную погрешность, которая со временем складывается в очень большие значения
Я не буду вдаваться в подробности, потому что мы автоматически избавимся от этой проблемы с адвекций, перейдя от scatter operation к gather operation и перефразировав вычисление диффузии. В новой схеме для диффузии значение ячеек косвенно задаётся их зависимостью от значения поля для каждой другой ячейки. Этот способ стабилен при больших шагах времени, однако если они становятся слишком большими, значения всё равно могут оставаться неточными. Но нам придётся пойти на компромисс: для поиска нового значения решать систему уравнений (подробнее об этом ниже). Нестабильность — беда многих физических симуляций, вы можете знать об этом из физической симуляции шарниров, которая разрушается и сходит с ума, когда кость в каждом кадре перемещается в новое место.
Процесс, который мы хотим реализовать в своих вычислениях, чтобы избавиться от проблемы сжимаемости, называется проецированием. Такое название дано потому, что мы проецируем наше поле на новый векторный базис, где один из этих базисов отвечает за завитки, а другой — за расхождение; однако я попытаюсь объяснить это более простым нематематическим языком. Проецирование — это когда мы берём поле векторов скоростей и преобразуем его так, чтобы жидкость не была сжата.
Для начала давайте выработаем интуитивное понимание того, как это можно сделать. Вещество не может сжиматься, не может иметь областей с повышенным и пониженным давлением. Когда мы вталкиваем воду в область так, что это повышает мгновенное давление (см. пример на Рисунке 4), вытолкнутые частицы пытаются переместиться из областей повышенного давления в области с пониженным давлением так, чтобы избежать сжимания. Частицы продолжат двигаться из областей с высоким в области с низким давлением, пока общая плотность частиц не станет одинаковой. Если мы сможем вычислить вектор скорости, вызванной этой разницей давлений (вызванной движением водоёма) и прибавить его к имеющемуся вектору скорости, то мы получим поле векторов скорости, не содержащее областей с увеличением давления. То есть мы получим поле векторов скорости, в котором не происходит сжатия. Можно посмотреть на это и иначе: мы компенсируем области, в которые нельзя втолкнуть воду и из которых нельзя её вытолкнуть, изменяя вектор скорости поля.
velocity_field + velocity_due_to_pressure_difference = new_velocity_with_no_pressure_difference
velocity_field = new_velocity_with_no_pressure_difference - velocity_due_to_pressure_difference
Ниже (см. Рисунок 11) мы рассмотрим связь между разностью давления и вызванным ею вектором скорости:
Difference_In_Pressure = -velocity_due_to_pressure_difference
Учитывая это выражение, окончательная формулировка будет такой:
velocity_field = new_velocity_with_no_pressure_difference + Difference_In_Pressure
Говоря техническими терминами, наше поле векторов скоростей имеет дивергенцию, и вычтя ту часть, за которую отвечает давление, мы получим компонент поля векторов скоростей без дивергенции. Представленное ниже выражение эквивалентно написанному выше. Однако это взгляд на явление под другим углом. Делается допущение о том, что текущее поле векторов скоростей состоит из двух разных типов векторов скоростей, части, которая не сжимает жидкости, и части, которая сжимает. Найдя ту часть, которая сжимает жидкость, и вычтя её из текущего вектора скорости, мы получим часть, которая не сжимает жидкость (что нам и нужно получить в конце каждого кадра).
velocity_field = Difference_In_Pressure + divergence_free_velocity
divergence_free_velocity = velocity_field -Difference_In_Pressure
Но как нам вычислить накопившееся в ячейке давление? Рассмотрим следующую схему.
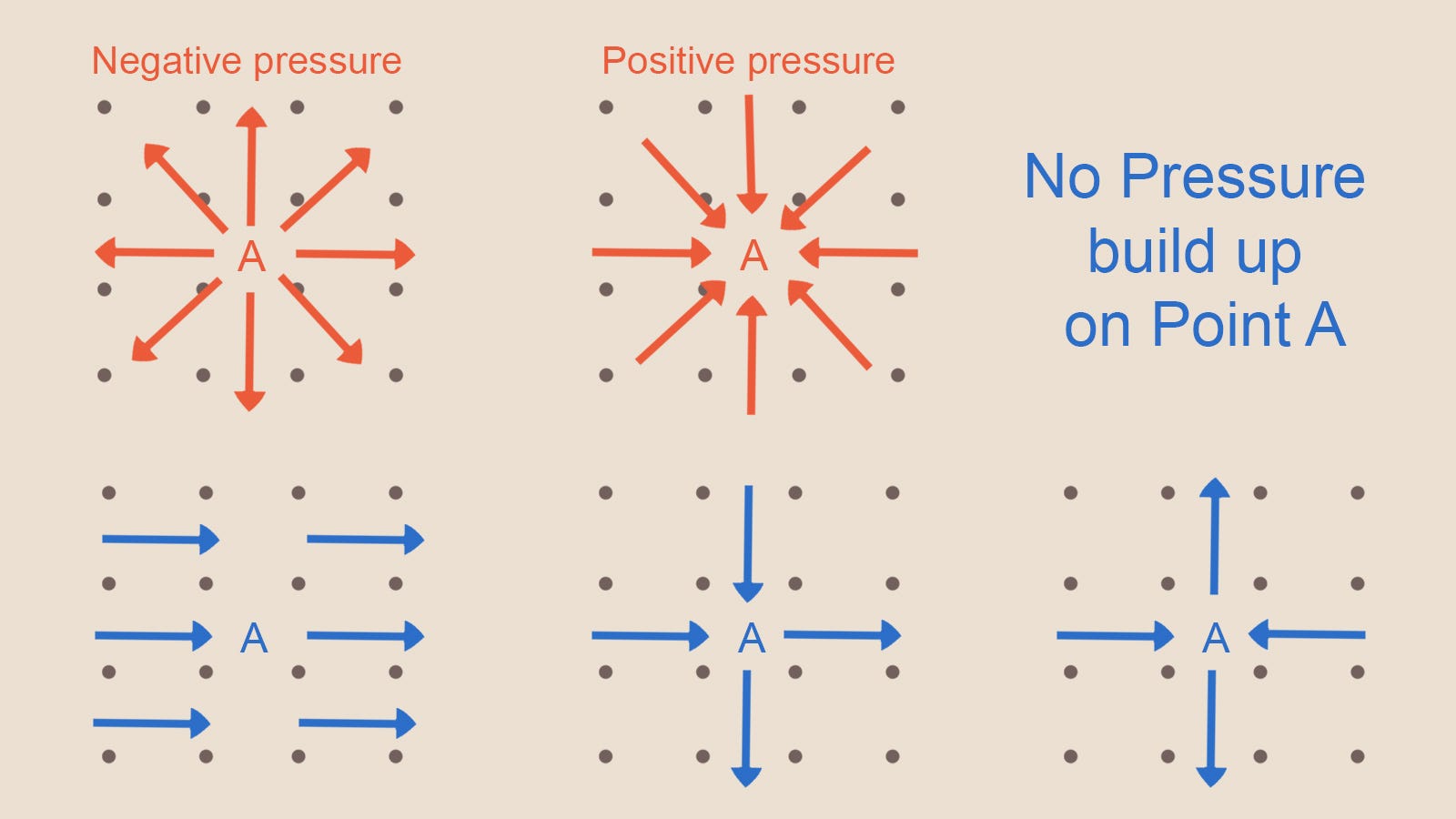
Рисунок 8 — Различные сценарии и то, как они приводят к давлению или его отсутствию
Посмотрев на эту схему, вы можете заметить, что нарастание давления в ячейке каким-то образом связано с векторами скорости соседних ячеек. Если количество веществ, попадающих в ячейку (из-за векторов скорости) равно количеству, покидающему ячейку, давление не нарастает. Если ячейку покидает больше вещества, чем поступает, то мы получаем отрицательное давление, если поступает больше, чем покидает, то положительное.
Для этого вычисления нам нужно рассмотреть соседние ячейки во всех измерениях, то есть не только по горизонтали, но и по вертикали. На Рисунке 8 посмотрите на схему в правом нижнем углу. Хотя горизонтально давление нарастает (оба вектора направлены в A), вертикально давление спадает (векторы направлены от A). То есть в сумме здесь не происходит нарастание давления.
Если мы вычтем компонент X векторов скорости ячеек справа и слева от интересующей нас ячейки, то получим число, сообщающее нам, движутся ли эти два вектора скорости в одном направлении по оси X, то есть вызывают ли соседние ячейки в этом измерении нарастание давления. Можно сделать то же самое для верхней и нижней ячеек (но с компонентом вектора скорости Y) и сложив два скалярных значения со знаком (вклад в нарастание давления вдоль горизонтальной и вертикальной осей), мы получим одно скалярное число, представляющее количество воды, сходящееся к центру ячейки, или расходящееся от него. Это количество и является дивергенцией поля векторов скоростей текущей ячейки.
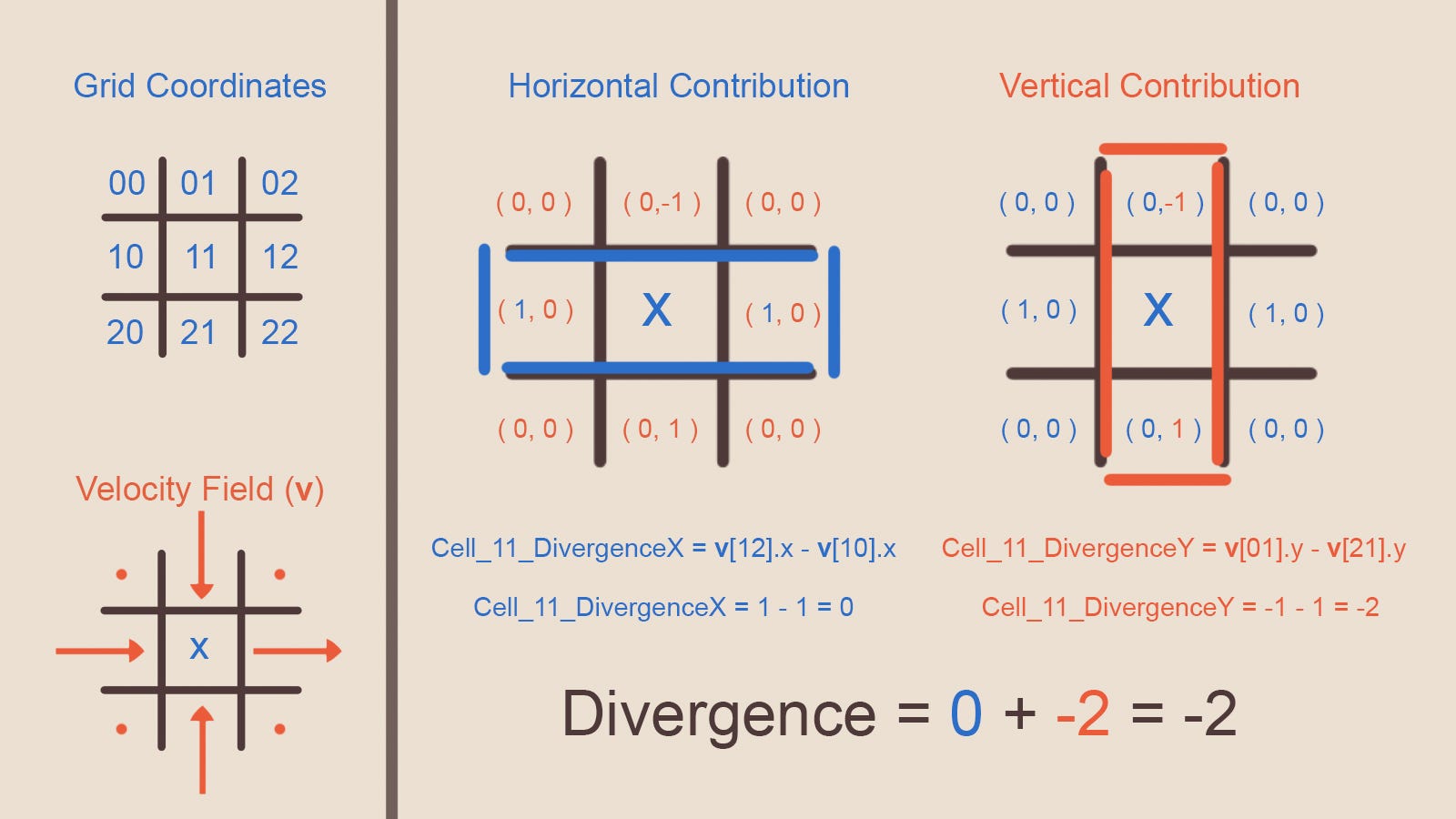
Рисунок 9 — Графическая схема и объяснение оператора дивергенции
На Рисунке 9 представлено визуальное объяснение. Если подставить это вычисление в функцию, то мы получим функцию дивергенции, получающую поле векторов и возвращающую поле скалярных значений. Эту функцию обычно называют оператором, это операция, которую можно проделать с полем, аналогично тому, как мы их складываем и вычитаем.
Однако дивергенция не является нашим давлением, хоть и связана с ним. Существуют разные способы объяснения связи между двумя этими понятиями. Математически сделать это достаточно просто, но поскольку я стремлюсь дать более интуитивное понимание, то сначала попробую иное, возможно, не самое точное объяснение явления. Однако оно намного проще описывает связь двух концепций.
Обозначим давление как . Как и вектор скорости,
также является полем (каждая ячейка имеет собственное значение для давления), но в отличие от вектора скорости, давление — это только скаляр. На данный момент мы не знаем значение
для каждой ячейки, однако давайте посмотрим, сможем ли мы создать уравнение, где значение давления для каждой ячейки будет неизвестным параметром. Посмотрите на Рисунок 9 и задайтесь вопросом: какой должна быть связь давления в центральной ячейке и её соседях, чтобы поле не имело дивергенции?
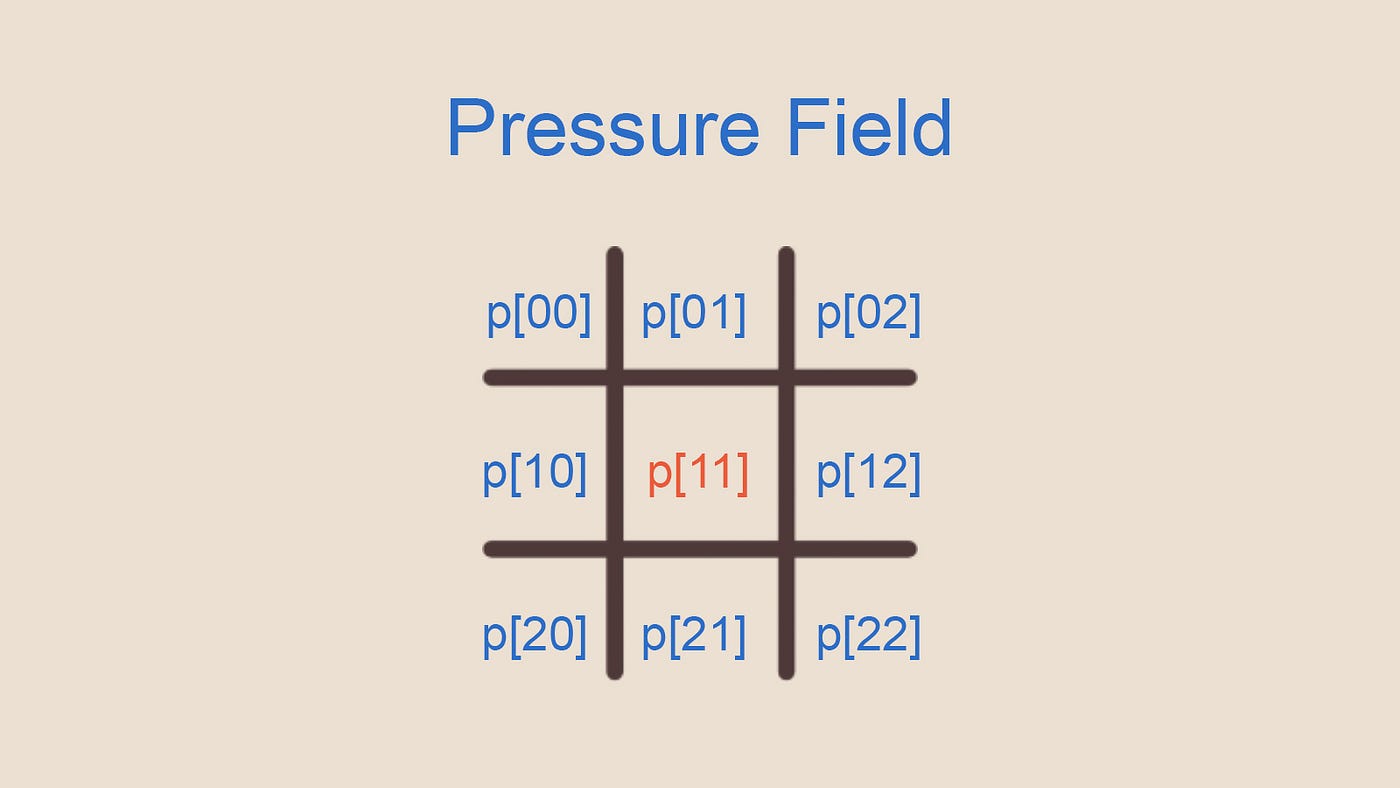
Рисунок 10 — Поле давления вокруг ячейки 11
Давление каждого поля влияет на 4 окружающих соседа, получая при этом четверть вклада от каждого из окружающих соседей. Поэтому чтобы в поле [11] возникло равновесие, давление в поле [11] должно быть равно сумме всех соседних давлений с соотношением 1 к 4. Можно посмотреть на это и иначе: давление в центральном поле должно быть равно среднему окружающих его давлений.
1/4 * (p[10] + p[01] + p[12] + p[21]) = p[11]
p[10] + p[01] + p[12] + p[21] = 4 * p[11]
Что происходит, когда эти два параметра неравны? Давайте вычислим разность между левой и правой частями:
(p[10] + p[01] + p[12] + p[21])- 4 * p[11]
В случае, когда давление в центре выше, чем вокруг, вещество будет выталкиваться из ячейки [11] и создастся отрицательное значение. Если окружающее давление выше, то вещество будет вталкиваться в [11] и значение будет положительным. Вы уже могли заметить, что это и есть дивергенция, и это значение, которое вычисляет наш оператор дивергенции, поэтому можно записать:
(p[10] + p[01] + p[12] + p[21])- 4 * p[11] = divergence(velocity_field)
Написанное выше ни в коем случае не является доказательством, и мы делаем достаточно свободные допущения, но повторюсь, наша задача — более интуитивное понимание взаимосвязи этих двух концепций. Прежде чем мы попытаемся решить показанное выше уравнение, я хотел бы показать вам альтернативный способ связывания давления с полем векторов скоростей.
Если у нас есть область высокого давления, окружённая областями низкого давления, вода будет перемещаться от высокого к низкому давлению. Это похоже на вагон поезда, где в одной половине куча народу, а другая относительно пуста. Люди будут перемещаться из заполненной половины в пустую, чтобы иметь больше пространства. Поэтому справедливо будет заявить, что разность давления приведёт к мгновенному вектору скорости, вызванному этим давлением:
difference_in_p => pressure_difference_induced_velocity
Чтобы преобразовать эту корреляцию в какое-то уравнение, вероятно, потребуется измерение массы или плотности (вспомним f=ma) или какая-то константа.
Как измерить изменение давления поля вдоль основной оси? Это достаточно простая операция, для ячейки [11] (Рисунок 10) мы вычитаем значение ячейки справа, ячейки слева, и результат становится компонентом X разности давлений, а затем можно то же самое сделать в вертикальном направлении, и это значение становится компонентом Y. Посмотрите для примера на Рисунок 11.
Приведённое ниже вычисление тоже является оператором, который можно записать как функцию. Чтобы объяснить функцию, я на секунду сделаю вид, что знаю значения поля давлений. Этот оператор называется оператором градиента, так как мы вычисляем градиент давления вдоль каждой из осей. Обратите внимание, что мы берём скалярное поле и получаем векторное поле. Возможно, вы уже заметили кое-что, связанное с направлением результирующего вектора и вектора скорости, который должна вызывать разность давлений. Если слева присутствует высокое давление, а справа — низкое, то оператор градиента создаёт вектор, направленный справа налево (как показано на Рисунке 11). Однако, как сказано ранее, частицы будут течь из областей высокого давления к низкому давлению, но никак не наоборот, то есть окончательная формулировка выглядит так:
difference_in_p = -pressure_difference_induced_velocity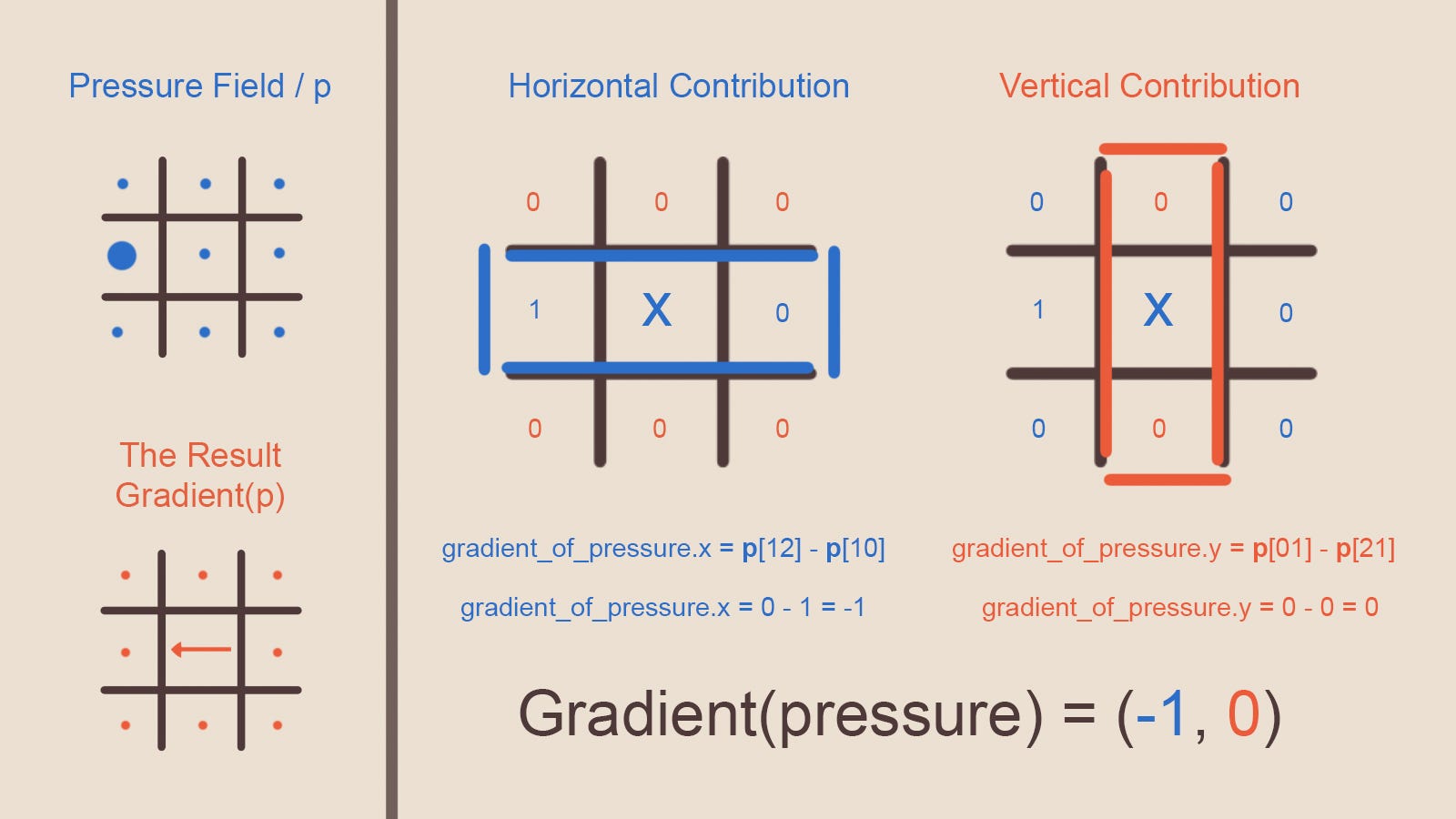
Рисунок 11 — Оператор градиента, вычисляющий градиент/разность давления в каждом измерении
Но как это связано с дивергенцией, можете спросить вы. В начале статьи мы задали такое отношение:
velocity_field = Difference_In_Pressure + divergence_free_velocity
Теперь мы можем записать его так:
velocity_field = Gradient(Pressure) + divergence_free_velocity
Наша задача — вычислить Pressure, которого у нас нет, но в этой формуле есть два неизвестных, Pressure и divergence_free_velocity, которая и является нашей конечной целью. Допустим, мы возьмём Divergence (velocity_field); если мы сделаем что-то с левой частью уравнения, то нужно будет сделать то же самое и с правой:
Divergence(velocity_field) = Divergence(Gradient(Pressure)) + Divergence(divergence_free_velocity)
Дивергенция (divergence_free_velocity) по определению равна нулю, потому что она обнуляется, и теперь у нас осталось одно уравнение и одна неизвестная! Итак, у нас осталось следующее:
Divergence(Gradient(Pressure)) = Divergence(velocity_field)
(p[10] + p[01] + p[12] + p[21])- 4 * p[11] = Divergence(velocity_field)
И это именно то же, что и выведенная ранее формулировка, если выполнить вычисления. Опять-таки, здесь сделано много допущений, например, разделение Divergence (A+B) на Divergence (A) + Divergence (B). Любопытный факт: дивергенция градиента — это тоже оператор, имеющий собственное название. Он называется оператором Лапласа и он является второй произвольной поля. Мы встретим его в других областях, например, в обработке геометрии, в контурных эффектах, компьютерном зрении, выявлении признаков и т.д.
Итак, теперь у нас есть уравнение для вычисления, где все значения (давления) неизвестны. Давайте выясним, как это сделать!
(p[10] + p[01] + p[12] + p[21])- 4 * p[11] = Divergence(velocity_field)Солверы
На первый взгляд кажется, что уравнение дивергенции давления невозможно решить, так как у нас есть 5 неизвестных и одно уравнение. На самом деле, у насесть уравнение для каждой ячейки в нашем поле. То есть если поле имеет размер N на N, то у нас есть N*N неизвестных и такое же количество уравнений. По сути, это система линейных уравнений, которую вы можете помнить из старшей школы!
Напомним, что система уравнений может выглядеть так:
Уравнение 1) y = x + 1
Уравнение 2) y = 5x — 2
Каждое из этих уравнений имеет собственный график и геометрически точка или точки (если они есть) пересечения этих графиков являются решением уравнения. Другими словами, парами значений x и y, при которых оба уравнения верны.
Из старшей школы вы можете помнить, что один из способов решения этой простой системы является подстановка: подставляем уравнение 1 во второе, вычисляем один параметр, а затем подставляем значение параметра в любое из уравнений, чтобы получить второй параметр. Примерно так:
Уравнение 2) y = (x + 1) = 5x — 2 <= так как y также является x +1
=> x — 5x = -2 -1 = -3
=> x = -3/-4 = ¾Подставляем в Уравнение 1) y = ¾ + 1 = 7/4
X = ¾ = 0,75, y = 7/4 = 1,75
Однако наша система совершенно непохожа на это уравнение. При сетке 128 на 128 у нас получится 16 тысяч неизвестных и уравнений. Нам совсем не хочется программировать что-то подобное на CPU или GPU. Кроме того, в нашей системе есть нечто уникальное: значение давления для каждой ячейки зависит только от 4 соседей и никак не связано с остальными 16 тысячами неизвестных. Так что если мы запишем одно из этих 16 тысяч уравнений, то увидим, что 99% неизвестных в каждом из них равны нулю. Поэтому мы и не хотим записывать их как матрицу и обращать её, так как большинство элементов будет равно нулю. Есть более быстрый способ!
Прежде чем я объясню этот быстрый способ, давайте совершим с нашей простой системой фокус. Преобразуем два уравнения так, чтобы в левой части у одного был X, а у другого Y.
Уравнение 1) y = x + 1Уравнение 2) x = y/5 + 2/5
Теперь возьмём любое начальное значение для x и y (например, ноль) и вставим его в правую часть. Получим:
Уравнение 1) y = 0 + 1 = 1Уравнение 2) x = 0/5 + 2/5 = 2/5 = 0,4
Теперь у нас есть новые значения X и Y, 0,4 and 1. Давайте повторим этот шаг ещё раз, но вместо нулей подставим новое значение.
Уравнение 1) y = 0.4 + 1 = 1,4Уравнение 2) x = 1/5 + 2/5 = 3/5 = 0,6
Мы можем повторять эти шаги множество раз, на каждом этапе беря предыдущее значение X и Y и снова вставляя его в уравнение. Давайте посмотрим, что произойдёт!
Шаг 0) Input (X, y) = (0, 0), output = (0.4, 1)Шаг 1) In (0.4, 1), out (0.6, 1.4)
Шаг 2) In (0.6, 1.4), out ((1.4 + 2)/5, 0.6 + 1) = (0.68, 1.6)
Шаг 3) In (0.68, 1.6), out ((1.6 + 2)/5, 0.68 + 1) = (0.72, 1.68)
Шаг 4) In (0.72, 1.68), out ((1.68+ 2)/5, 0.72 + 1) = (0.736, 1.72)
Магия! Даже через четыре шага мы уже почти получили решение. Можно повторить это ещё много раз и рано или поздно приблизиться к точному решению. Этот способ называется итеративным солвером, точнее, методом (солвером) Якоби. Удобно то, что это решение также применимо и к нашей системе, и его очень легко реализовать на GPU. Нам достаточно просто сохранять значение давления в каждой ячейке (как текстуру или вычислительный буфер) на каждом этапе нашей итерации и подставлять его на следующем этапе.
Существует множество разных солверов, некоторые из них требуют меньше памяти, другие — меньше шагов для достаточного приближения к решению, а третьи обеспечивают повышенную точность (помните, что из-за погрешностей вычислений с плавающей запятой важно то, какие числа умножаются на какие, и в каком порядке). Я использую здесь метод Якоби, потому что остальные солверы трудно реализовать на GPU. В порядке повышения сложности: метод Якоби — метод Гаусса-Зейделя — метод релаксации — многосеточный метод. Существуют и ещё более сложные солверы, с которыми вы столкнётесь в научно-технической работе, но к нашему случаю они не относятся.
Однако остаётся один вопрос: почему это работает? Наиболее точным способом объяснения солверов является использование их матричной формы (диагональной матрицы Якоби для метода Якоби, нижний треугольник для метода Гаусса-Зейделя, специальным образом созданный треугольник для метода релаксации и мультисетка для многосеточного метода), при помощи которой мы также можем запросто объяснить стабильность, точность и т.п. Но я бы хотел избежать этого, чтобы не отпугнуть читателей, желающих обрести базовое понимание того, что они кодят.
Для своего объяснения я бы хотел использовать метод Гаусса-Зейделя вместо солвера Якоби, который мы используем в своей реализации, потому что он достигает результата вдвое быстрее. Разница между двумя этими методами проста, в методе Гаусса-Зейделя мы мгновенно используем значения, вычисленные для наших неизвестных в вычислениях следующих неизвестных, не ожидая целый этап. То есть в приведённом выше примере вместо подстановки 0 и 0 вместо X и Y мы подставим 0 вместо X, вычислим, что Y равен 1, и вместо подстановки 0 вместо Y в уравнение 2 мы сразу же используем значение 1, вычисленное на основе X, что даст нам 0,6. Затем мы переходим на этап 2 и подставляем 0,6 вместо X, чтобы найти новый Y (1,6), и так далее. Заметьте, что мы, по сути, доходим до того же решения, но за половину шагов. Фантастика, правда? Но существует проблема с GPU и многопоточностью, так как мы решаем все ячейки одновременно и не можем использовать эту технику без чего-то вроде красно-чёрного паттерна доступа, который уменьшая вдвое количество этапов, удваивает количество вызовов отрисовки. Поэтому выигрыш минимален.
Вернёмся к нашей простой системе. Ниже показан график двух уравнений. Помните, что решение находится в точке их пересечения. Мы уже знаем эти значения из аналитического решения, это X= 0,75 и Y=1,75
Уравнение 1) y = x + 1Уравнение 2) y = 5x — 2
Что же на самом деле выполняет наш солвер? В качестве начальных значений давайте возьмём 3 вместо x (ранее мы брали вместо начального значения ноль, но выбрать можно любое). На шаге 1 мы находим значение Y, которое имеет наш график при X = 3. Затем мы смотрим на графике 2, какое значение X соответствует только что найденному Y. Повторяя этот процесс, мы можем заметить, что выполняем проецирование графиков друг на друга, в ту и другую сторону, и поскольку эти графики сходятся к одной точке, мы продолжаем приближаться к точке пересечения как мяч, катящийся вниз по склону.
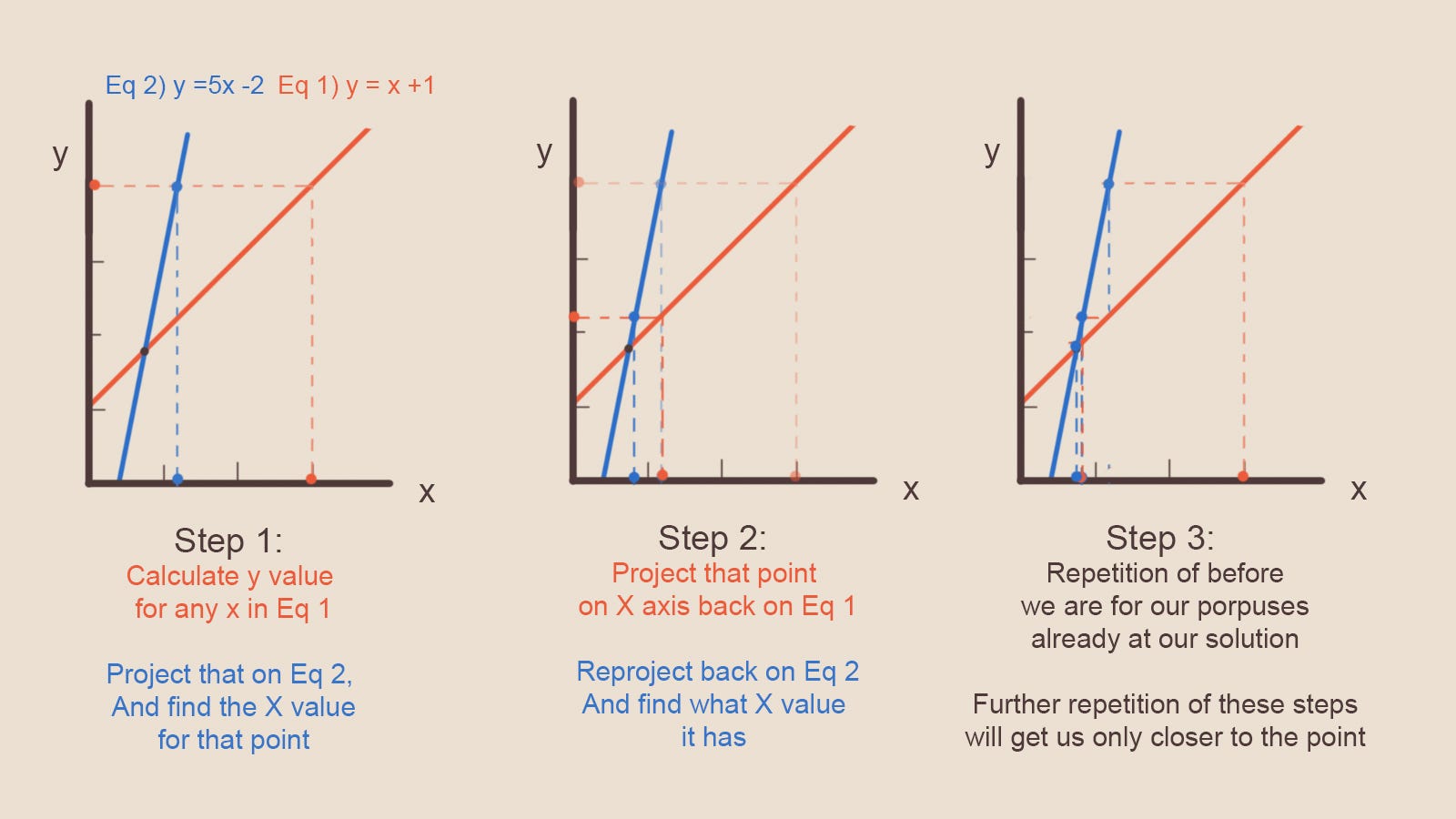
Рисунок 12 — Графическое представление солверов.
Тогда на N-ном шаге мы получим нечто подобное. Красивая игра в пинг-понг всегда будет приближаться к истинному решению, но никогда не достигнет его и не перескочит его.
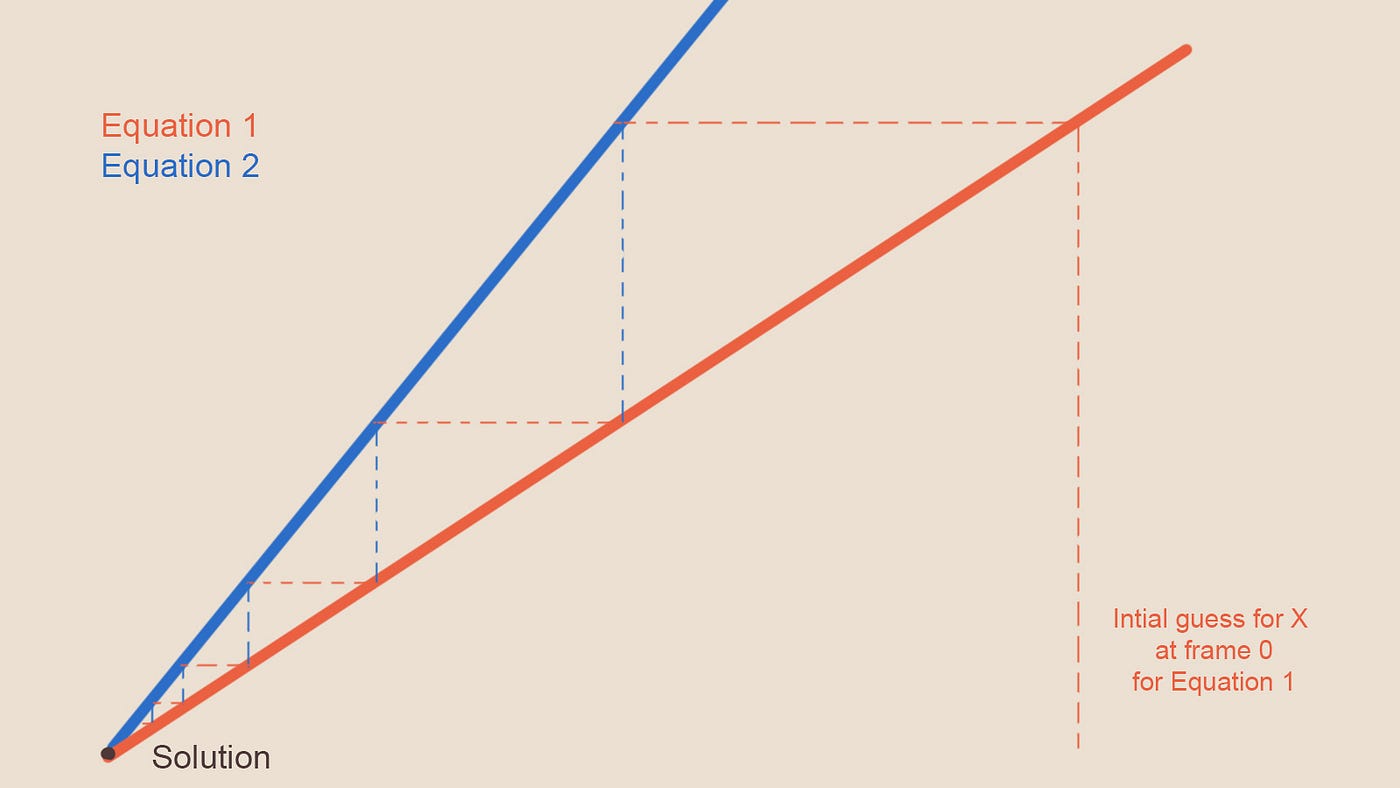
Рисунок 13 — Солверы на N-ном шаге, всегда приближаются к ответу, но никогда его не достигают
Разумеется, это работает не для всех уравнений. Два графика могут не сойтись или иметь несколько решений, и т.д. Но в нашем случае это работает.
Чтобы использовать солвер, мы перепишем уравнение таким образом, чтобы поле посередине находилось слева. Тогда для любой ячейки с координатами i и j мы получим:
Solve(Velocity_Divergence)
{
p_new[i, j] =((p[i+1,j] + p[i,j+1] + p[i-1,j] + p[i,j-1]) - Velocity_Divergence[i, j])/4
}
После запуска этой программы мы можем сделать следующее:
© Habrahabr.ru
